Chapter 2 Data Analysis Section 2 1 Describing

Chapter 2 Data Analysis Section 2. 1 Describing Location in a Distribution

Describing Location in a Distribution LEARNING TARGETS By the end of this section, you should be able to: üFIND and INTERPRET the percentile of an individual value within a distribution of data. üESTIMATE percentiles and individual values using a cumulative relative frequency graph. üFIND and INTERPRET the standardized score (z-score) of an individual value within a distribution of data. üDESCRIBE the effect of adding, subtracting, multiplying by, or dividing by a constant on the shape, center, and variability of a distribution of data. Starnes/Tabor, The Practice of Statistics

Measuring Location: Percentiles One way to describe the location of a value in a distribution is to tell what percent of observations are less than it. An individual’s percentile is the percent of values in a distribution that are less than the individual’s data value. Starnes/Tabor, The Practice of Statistics

Measuring Location: Percentiles One way to describe the location of a value in a distribution is to tell what percent of observations are less than it. An individual’s percentile is the percent of values in a distribution that are less than the individual’s data value. Jenny earned a score of 86 on her test. How did she perform relative to the rest of the class? 6|7 7 | 2334 7 | 5777899 8 | 00123334 8 | 569 9 | 03 Starnes/Tabor, The Practice of Statistics

Measuring Location: Percentiles One way to describe the location of a value in a distribution is to tell what percent of observations are less than it. An individual’s percentile is the percent of values in a distribution that are less than the individual’s data value. Jenny earned a score of 86 on her test. How did she perform relative to the rest of the class? 6|7 7 | 2334 7 | 5777899 8 | 00123334 8 | 569 9 | 03 Jenny’s score was greater than 21 of the 25 observations. Since 21 of the 25, or 84%, of the scores are below hers, Jenny’s score is at the 84 th percentile in the distribution of test scores for the class. Starnes/Tabor, The Practice of Statistics

Cumulative Relative Frequency Graphs A cumulative relative frequency graph plots a point corresponding to the cumulative relative frequency in each interval at the smallest value of the next interval, starting with a point at a height of 0% at the smallest value of the first interval. Consecutive points are then connected with a line segment to form the graph. Starnes/Tabor, The Practice of Statistics

Cumulative Relative Frequency Graphs A cumulative relative frequency graph plots a point corresponding to the cumulative relative frequency in each interval at the smallest value of the next interval, starting with a point at a height of 0% at the smallest value of the first interval. Consecutive points are then connected with a line segment to form the graph. Age of First 44 Presidents When They Were Inaugurated Age Frequency 40 -44 2 45 -49 7 50 -54 13 55 -59 12 60 -64 7 65 -69 3 Starnes/Tabor, The Practice of Statistics

Cumulative Relative Frequency Graphs A cumulative relative frequency graph plots a point corresponding to the cumulative relative frequency in each interval at the smallest value of the next interval, starting with a point at a height of 0% at the smallest value of the first interval. Consecutive points are then connected with a line segment to form the graph. Age of First 44 Presidents When They Were Inaugurated Age Frequency Relative frequency 40 -44 2 2/44 = 4. 5% 45 -49 7 7/44 = 15. 9% 50 -54 13 13/44 = 29. 5% 55 -59 12 12/44 = 34% 60 -64 7 7/44 = 15. 9% 65 -69 3 3/44 = 6. 8% Starnes/Tabor, The Practice of Statistics

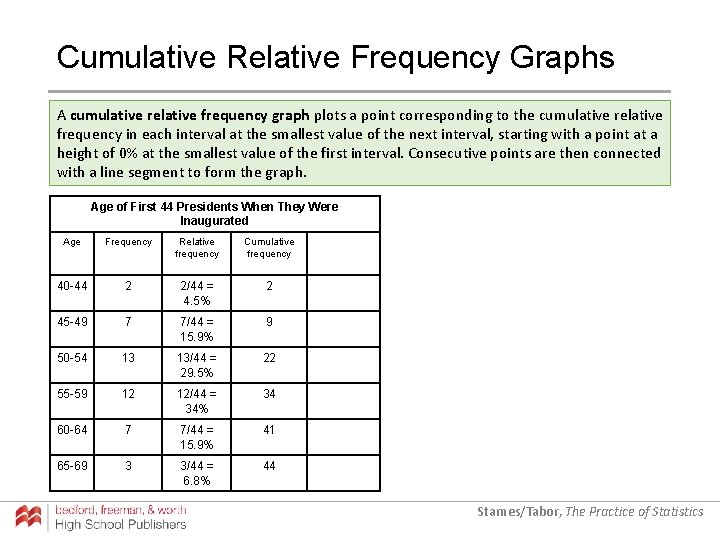
Cumulative Relative Frequency Graphs A cumulative relative frequency graph plots a point corresponding to the cumulative relative frequency in each interval at the smallest value of the next interval, starting with a point at a height of 0% at the smallest value of the first interval. Consecutive points are then connected with a line segment to form the graph. Age of First 44 Presidents When They Were Inaugurated Age Frequency Relative frequency Cumulative frequency 40 -44 2 2/44 = 4. 5% 2 45 -49 7 7/44 = 15. 9% 9 50 -54 13 13/44 = 29. 5% 22 55 -59 12 12/44 = 34% 34 60 -64 7 7/44 = 15. 9% 41 65 -69 3 3/44 = 6. 8% 44 Starnes/Tabor, The Practice of Statistics

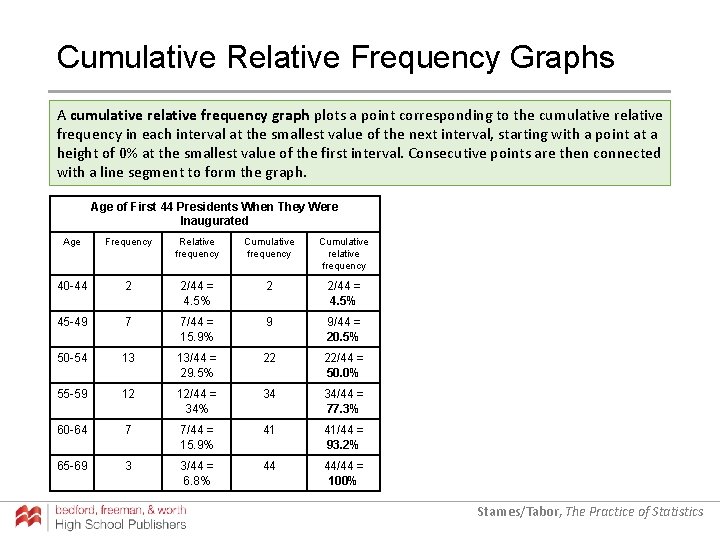
Cumulative Relative Frequency Graphs A cumulative relative frequency graph plots a point corresponding to the cumulative relative frequency in each interval at the smallest value of the next interval, starting with a point at a height of 0% at the smallest value of the first interval. Consecutive points are then connected with a line segment to form the graph. Age of First 44 Presidents When They Were Inaugurated Age Frequency Relative frequency Cumulative relative frequency 40 -44 2 2/44 = 4. 5% 45 -49 7 7/44 = 15. 9% 9 9/44 = 20. 5% 50 -54 13 13/44 = 29. 5% 22 22/44 = 50. 0% 55 -59 12 12/44 = 34% 34 34/44 = 77. 3% 60 -64 7 7/44 = 15. 9% 41 41/44 = 93. 2% 65 -69 3 3/44 = 6. 8% 44 44/44 = 100% Starnes/Tabor, The Practice of Statistics

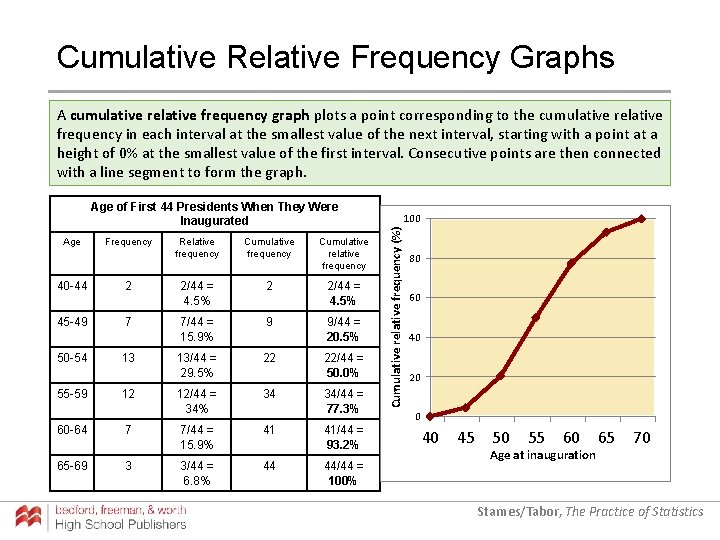
Cumulative Relative Frequency Graphs A cumulative relative frequency graph plots a point corresponding to the cumulative relative frequency in each interval at the smallest value of the next interval, starting with a point at a height of 0% at the smallest value of the first interval. Consecutive points are then connected with a line segment to form the graph. Age Frequency Relative frequency Cumulative relative frequency 40 -44 2 2/44 = 4. 5% 45 -49 7 7/44 = 15. 9% 9 9/44 = 20. 5% 13/44 = 29. 5% 22 50 -54 13 22/44 = 50. 0% 55 -59 12 12/44 = 34% 34 34/44 = 77. 3% 60 -64 7 7/44 = 15. 9% 41 41/44 = 93. 2% 65 -69 3 3/44 = 6. 8% 44 44/44 = 100% 100 Cumulative relative frequency (%) Age of First 44 Presidents When They Were Inaugurated 80 60 40 20 0 40 45 50 55 60 Age at inauguration 65 70 Starnes/Tabor, The Practice of Statistics

Measuring Position: z-Scores A z-score tells us how many standard deviations from the mean an observation falls, and in what direction. If x is an observation from a distribution that has known mean and standard deviation, the standardized score of x is: A standardized score is often called a z-score. Starnes/Tabor, The Practice of Statistics

Measuring Position: z-Scores Jenny earned a score of 86 on her test. The class mean is 80 and the standard deviation is 6. 07. Find and interpret her standardized score. Starnes/Tabor, The Practice of Statistics

Measuring Position: z-Scores Jenny earned a score of 86 on her test. The class mean is 80 and the standard deviation is 6. 07. Find and interpret her standardized score. Jenny’s test score is 0. 99 standard deviations above the class mean of 80. Starnes/Tabor, The Practice of Statistics

Measuring Position: z-Scores Jenny earned a score of 86 on her test. The class mean is 80 and the standard deviation is 6. 07. Find and interpret her : CAUTION standardized score. nce a t s i d a s ea r o c s z the e f i h t e t t a e c r i p d r te s in y a w l A. Do not in n mea e than h t s s m e l o r r f o ” ) ove b “away a ( n a h t ter a e r g s i e u val an. e m e h t ) (below Jenny’s test score is 0. 99 standard deviations above the class mean of 80. Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Adding or Subtracting a Constant Adding the same positive number a to (subtracting a from) each observation: Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Adding or Subtracting a Constant Adding the same positive number a to (subtracting a from) each observation: • Adds a to (subtracts a from) measures of center and location (mean, five-number summary, percentiles) Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Adding or Subtracting a Constant Adding the same positive number a to (subtracting a from) each observation: • Adds a to (subtracts a from) measures of center and location (mean, five-number summary, percentiles) • Does not change measures of variability (range, IQR, standard deviation) Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Adding or Subtracting a Constant Adding the same positive number a to (subtracting a from) each observation: • Adds a to (subtracts a from) measures of center and location (mean, five-number summary, percentiles) • Does not change measures of variability (range, IQR, standard deviation) • Does not change the shape of the distribution Starnes/Tabor, The Practice of Statistics

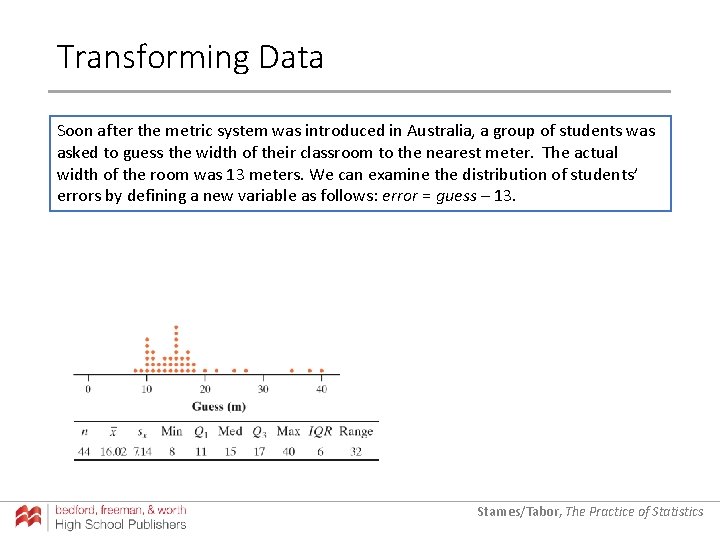
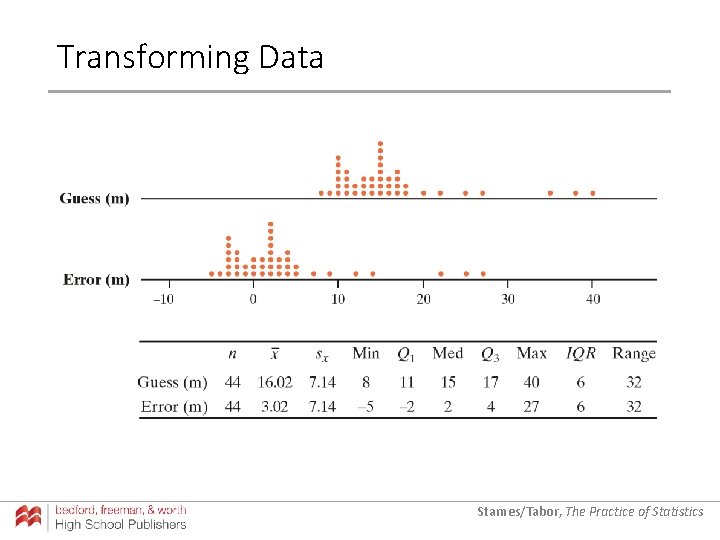
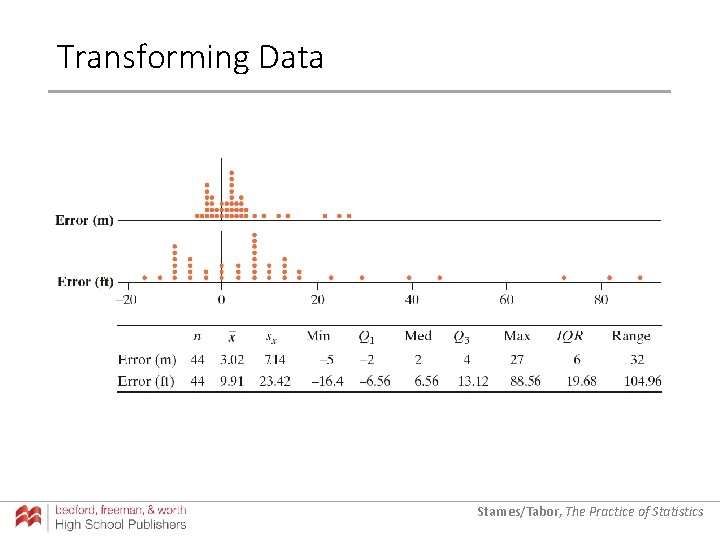
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. Starnes/Tabor, The Practice of Statistics

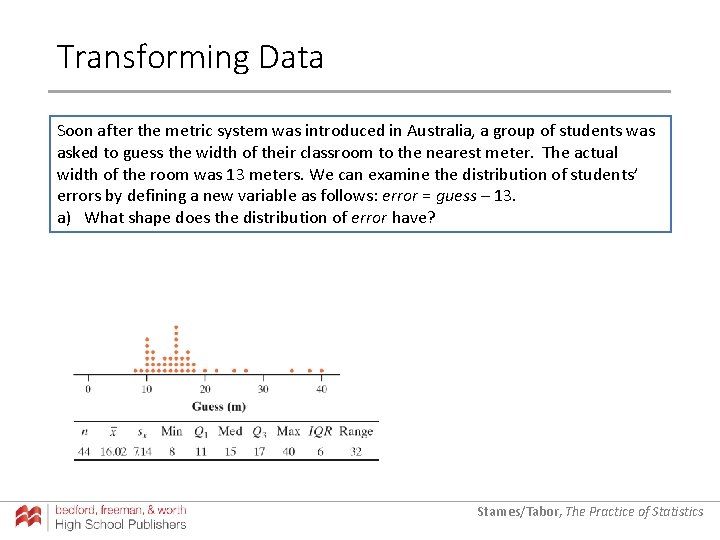
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. a) What shape does the distribution of error have? Starnes/Tabor, The Practice of Statistics

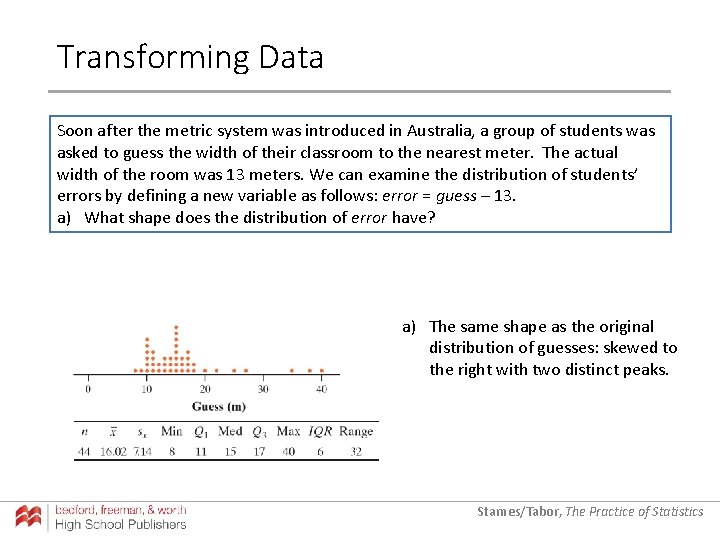
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. a) What shape does the distribution of error have? a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. Starnes/Tabor, The Practice of Statistics

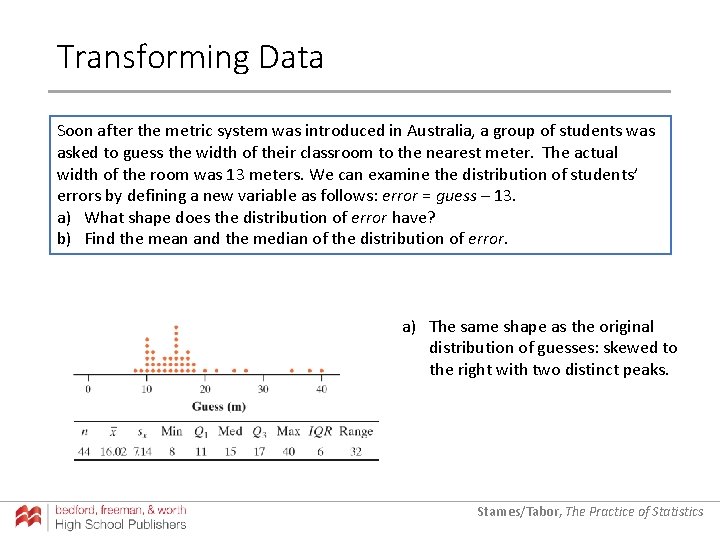
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. a) What shape does the distribution of error have? b) Find the mean and the median of the distribution of error. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. Starnes/Tabor, The Practice of Statistics

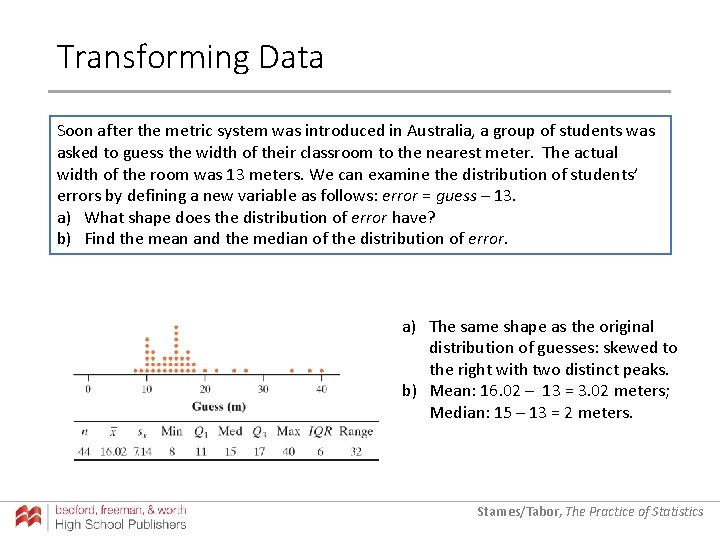
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. a) What shape does the distribution of error have? b) Find the mean and the median of the distribution of error. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. b) Mean: 16. 02 – 13 = 3. 02 meters; Median: 15 – 13 = 2 meters. Starnes/Tabor, The Practice of Statistics

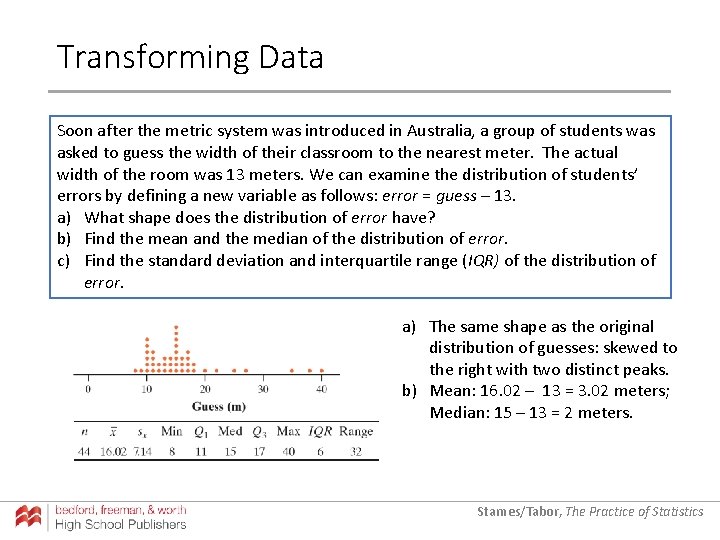
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. a) What shape does the distribution of error have? b) Find the mean and the median of the distribution of error. c) Find the standard deviation and interquartile range (IQR) of the distribution of error. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. b) Mean: 16. 02 – 13 = 3. 02 meters; Median: 15 – 13 = 2 meters. Starnes/Tabor, The Practice of Statistics

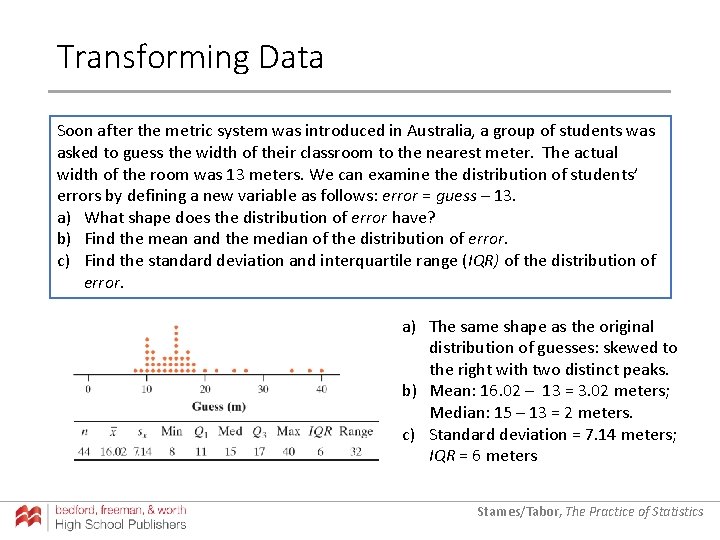
Transforming Data Soon after the metric system was introduced in Australia, a group of students was asked to guess the width of their classroom to the nearest meter. The actual width of the room was 13 meters. We can examine the distribution of students’ errors by defining a new variable as follows: error = guess – 13. a) What shape does the distribution of error have? b) Find the mean and the median of the distribution of error. c) Find the standard deviation and interquartile range (IQR) of the distribution of error. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. b) Mean: 16. 02 – 13 = 3. 02 meters; Median: 15 – 13 = 2 meters. c) Standard deviation = 7. 14 meters; IQR = 6 meters Starnes/Tabor, The Practice of Statistics

Transforming Data Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Multiplying or Dividing by a Constant Multiplying (or dividing) each observation by the same positive number b: Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Multiplying or Dividing by a Constant Multiplying (or dividing) each observation by the same positive number b: • Multiplies (divides) measures of center and location by b (mean, five-number summary, percentiles) by b Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Multiplying or Dividing by a Constant Multiplying (or dividing) each observation by the same positive number b: • Multiplies (divides) measures of center and location by b (mean, five-number summary, percentiles) by b • Multiplies (divides) measures of variability by b (range, IQR, standard deviation) Starnes/Tabor, The Practice of Statistics

Transforming Data Transforming converts the original observations from the original units of measurements to another scale. Transformations can affect the shape, center, and spread of a distribution. The Effect of Multiplying or Dividing by a Constant Multiplying (or dividing) each observation by the same positive number b: • Multiplies (divides) measures of center and location by b (mean, five-number summary, percentiles) by b • Multiplies (divides) measures of variability by b (range, IQR, standard deviation) • Does not change the shape of the distribution Starnes/Tabor, The Practice of Statistics

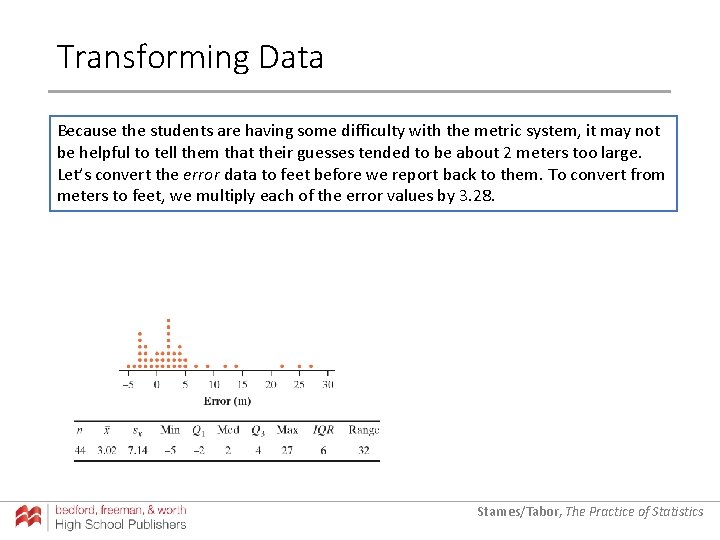
Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. Starnes/Tabor, The Practice of Statistics

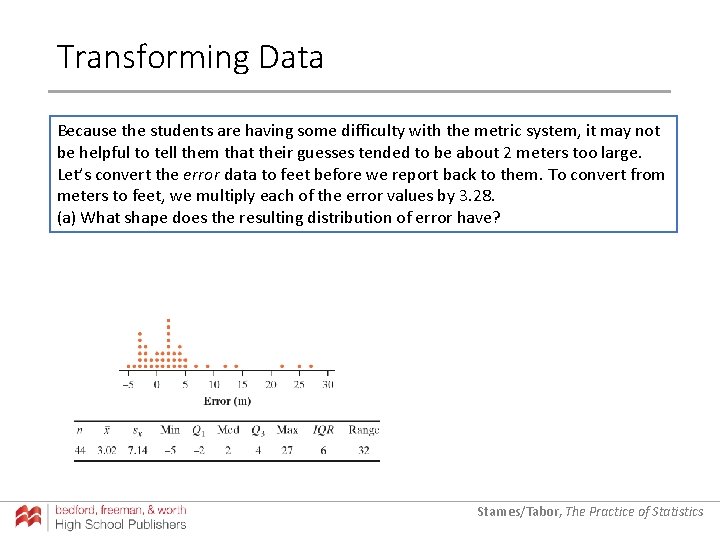
Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. (a) What shape does the resulting distribution of error have? Starnes/Tabor, The Practice of Statistics

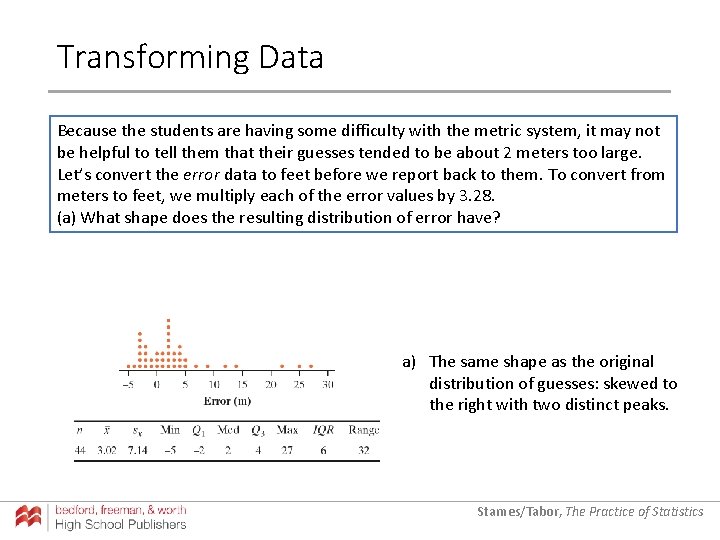
Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. (a) What shape does the resulting distribution of error have? a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. Starnes/Tabor, The Practice of Statistics

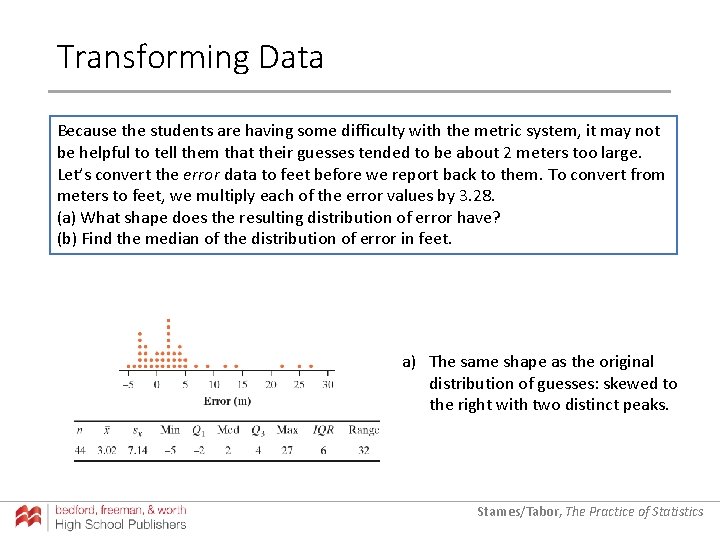
Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. (a) What shape does the resulting distribution of error have? (b) Find the median of the distribution of error in feet. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. Starnes/Tabor, The Practice of Statistics

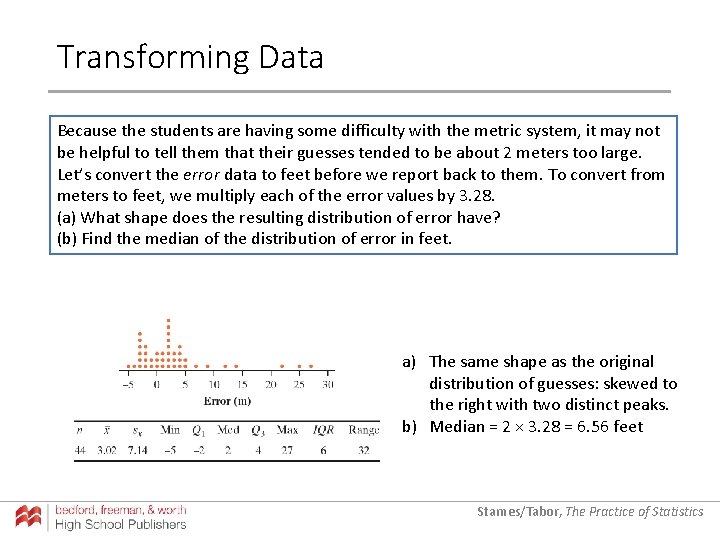
Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. (a) What shape does the resulting distribution of error have? (b) Find the median of the distribution of error in feet. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. b) Median = 2 × 3. 28 = 6. 56 feet Starnes/Tabor, The Practice of Statistics

Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. (a) What shape does the resulting distribution of error have? (b) Find the median of the distribution of error in feet. (c) Find the interquartile range (IQR) of the distribution of error in feet. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. b) Median = 2 × 3. 28 = 6. 56 feet Starnes/Tabor, The Practice of Statistics

Transforming Data Because the students are having some difficulty with the metric system, it may not be helpful to tell them that their guesses tended to be about 2 meters too large. Let’s convert the error data to feet before we report back to them. To convert from meters to feet, we multiply each of the error values by 3. 28. (a) What shape does the resulting distribution of error have? (b) Find the median of the distribution of error in feet. (c) Find the interquartile range (IQR) of the distribution of error in feet. a) The same shape as the original distribution of guesses: skewed to the right with two distinct peaks. b) Median = 2 × 3. 28 = 6. 56 feet c) IQR = 6 × 3. 28 = 19. 68 feet Starnes/Tabor, The Practice of Statistics

Transforming Data Starnes/Tabor, The Practice of Statistics

Section Summary LEARNING TARGETS After this section, you should be able to: üFIND and INTERPRET the percentile of an individual value within a distribution of data. üESTIMATE percentiles and individual values using a cumulative relative frequency graph. üFIND and INTERPRET the standardized score (z-score) of an individual value within a distribution of data. üDESCRIBE the effect of adding, subtracting, multiplying by, or dividing by a constant on the shape, center, and variability of a distribution of data. Starnes/Tabor, The Practice of Statistics

Assignment 2. 1 p. 104 -109 #2 -30 EOE (Every Other Even) and 33 -39 all (2, 6, 10, 14, 18, 22, 26, 30, 33 -39) If you are stuck on any of these, look at the odd before or after and the answer in the back of your book. If you are still not sure text a friend or me for help (before 8 pm). Tomorrow we will check homework and review for 2. 1 Quiz. Starnes/Tabor, The Practice of Statistics