Chapter 2 Data Analysis Objectives Define SI base

Chapter 2 Data Analysis

Objectives: • Define SI base units for time, length, mass and temperature • Use prefixes with units • Compare the derived units for volume and density • Use scientific notation

Objectives (cont’d) • Define and compare accuracy and precision • Use significant figures and rounding to reflect the certainty of data • Use % error to describe the accuracy of experimental data • Correctly create, read and interpret graphs

Terms to know…. Base unit Derived unit Meter Length Liter Kelvin kilogram density second accuracy precision conversion factor

Terms to know…. (Cont’d) Random error Systematic error Independent variable Dependent variable

Units of Measurement SI Quantity Base unit symbol Time Second Length Meter Mass Kilogram Temperature Kelvin Amt of a substance Mole s m kg K mol

You can change any base unit with a prefix Some prefixes are for large numbers: giga (G) 109 mega (M) 106 kilo (k) 1000 gigameter megameter kilometer

And some for smaller ones… deci 0. 1 10 -1 centi milli micro nano pico 0. 01 0. 000 001 0. 000 000 001 10 -2 10 -3 10 -6 10 -9 10 -12

So, how much is…. A milliliter? A centigram? A kilowatt? A nanometer? A picosecond? ________ ____

Base vs derived units • A base unit is a single unit and is measured directly--Example: - time in seconds with a stopwatch - mass in grams with a balance - length in cm with a ruler

A derived unit is a combination of two or more base units Example: speed density meters/sec km/hr g/m. L or g/cm 3 and …….

Volume is a derived unit = Lxwxh 1 liter = 10 cm x 10 cm = 1000 cm 3 or = 1 dm* x 1 dm = 1 dm 3 * 10 cm = 1 decimeter
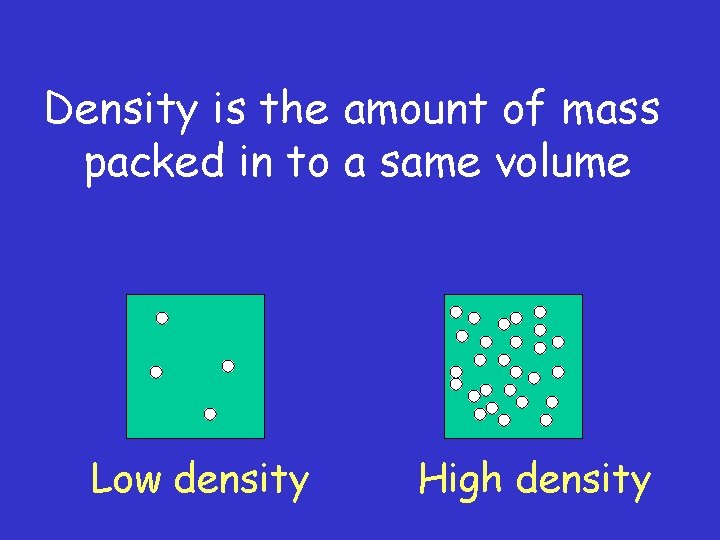
Density is the amount of mass packed in to a same volume Low density High density

Density = mass volume Example #1: A 121. 5 g sample of aluminum has a volume of 45 cm 3. What is the density of Al?
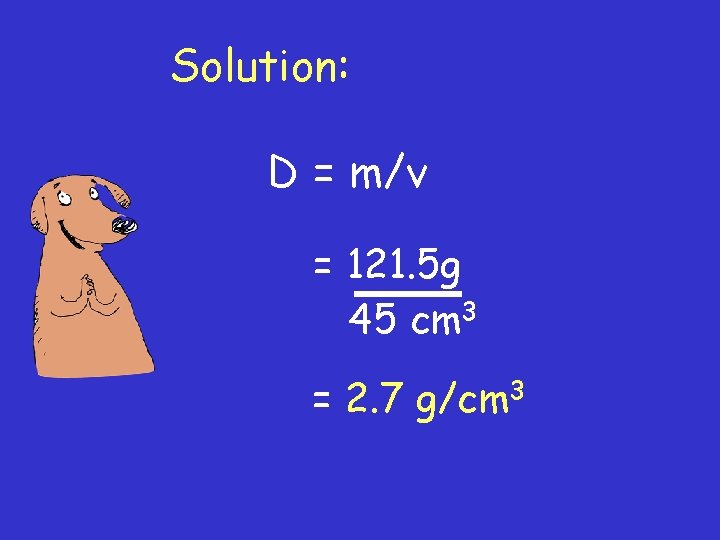
Solution: D = m/v = 121. 5 g 45 cm 3 = 2. 7 g/cm 3

Another density problem: Example #2: What would be the mass of 1000 m. L of liquid mercury, density 13. 5 g/m. L?

Solution: D= m v 13. 5 g/m. L = m 1000 m. L (13. 5 g/m. L) (1000 m. L) = 13 500 g = 13. 5 kg

Scientific notation • Used to simplify reading numbers that are very large or very small • In normal scientific notation there is one number to the left of the decimal Ex. : 5. 66 x 1013

Another version of scientific notation is called Engineering mode • In Engineering mode two numbers are left in front of the decimal Ex: 56. 6 x 10 12

You will see both in your Scientific calculator Chemists typically use normal scientific notation -19 10 Ex: 1. 66 x 6. 022 x 1023

Dimensional analysis -is a way of solving problems that focuses on the units rather than the numbers to solve the problem -solves problems by using a conversion factor

A conversion factor is --- -a ratio of equivalent values expressed in different units -a conversion factor is like multiplying a number by 1 such as……

12 inches 1 foot = a conversion factor 1 hour = a conversion 3600 seconds factor Same thing =1
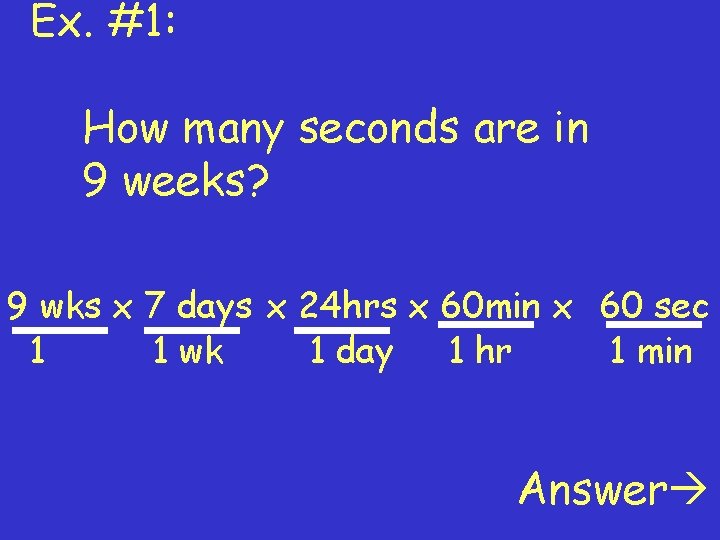
Ex. #1: How many seconds are in 9 weeks? 9 wks x 7 days x 24 hrs x 60 min x 60 sec 1 1 wk 1 day 1 hr 1 min Answer

Answer: Notice how the units canceled out: 9 wks x 7 days x 24 hrs x 60 min x 60 sec 1 1 wk 1 day 1 hr 1 min = 5 443 200 sec

Ex. #2: In Europe, the posted speed limit is 90 km/hr – what would that be in miles/hr? 1 km = 0. 62 miles

Ex. #2 90 km x 0. 62 miles = 55. 8 miles 1 hr 1 km hr

Ex. #3: If a baseball player hit 70 home runs in a single season, and it’s 90 feet between each of the four bases, how many miles did he run that year in just home runs? Try this on your own paper. 1 mile = 5280 feet Answer

Answer #3 70 home runs x 360 ft x 1 mile 1 season 1 homerun 5280 ft = 4. 77 miles/season

How reliable are measurements? Scientists are concerned with • the accuracy of a measurement • the precision of a measurement

Accuracy = how close your answer comes to the “real answer, ” the accepted value Poor accuracy Good accuracy

Precision • Precision refers to how close a series of measurements are to each other • Precision is the “repeatability” of a measurement

Remember… …accuracy is typically determined by the equipment you use Did you use a good analytical balance or a old triple-beam balance?

While precision is … determined by how good YOU are with the equipment provided. Can you do over and get similar answers?

Poor precision Poor accuracy Good precision Poor accuracy

Good precision Good accuracy

Reporting measurements • Every measurement has some reported error or uncertainty • Uncertainty is assumed to be ± one unit in the last reported place

Example: You record 1. 24 g as the mass of a sample. This is automatically assumed to be between 1. 23 and 1. 25 or ± 0. 01 grams.

When reading normal laboratoryequipment, avoid parallax errors. Take measurements from the bottom of the meniscus when observing at eye Level.

Read the bottom of the meniscus in a graduated cylinder- while holding it at eye level.

What about errors? • All experiments have some errors! - human error - mechanical error • An error can be a random error (because it is equally likely to be high or low)

Error (cont’d) • Random errors are sometimes called indeterminate errors, because it is largely due to the limitations of the lab equipment you use

Error (cont’d) • You can also have systematic errors (determinate errors). These are often caused by faulty measurements or problems with your measuring device. (Did you zero your balance before using it? )

Finding a % error is the ratio of your error (How much you were off) divided by the actual accepted answer.

Ex. #1 Donna calculated the density of aluminum to be 2. 52 g/m. L. The accepted density of aluminum is 2. 70 g/m. L. What is her % error? Error x 100 = % error Accepted (2. 70 -2. 52) x 100= 6. 67% error 2. 70

Ex. #2 Bill did the same lab as Donna, But he found the density of Al to be 2. 95 g/m. L. What is his % error? Error* x 100 = % error Accepted (2. 95 -2. 70) x 100= 9. 26% 2. 70 * Error is always considered positive

Ex. #3: Your turn Juan calculated the density of Copper to be 9. 34 g/m. L. What was his % error? (Find density using the chart on pg 914 in your textbook. ) Answer

Ex. #3 Answer Error x 100 = % error Accepted (9. 34 -8. 92) x 100 = 4. 71% 8. 92

Significant figures When you measure using any scientific instrument, your answer’s precision depends upon the equipment you used.

• The digits that are reported when reading a scientific instrument called significant figures. • Significant figures include all KNOWN digits plus one ESTIMATED digit.

2 3 4 • This ruler would read 2. 5_ cm We would probably say 2. 56 cm or maybe even 2. 57 cm. • The 2. 5 are certain digits the last digit is an estimate.

Rules for significant figures: 1. Non-zero numbers are always significant. Example: 957 = 3 SF 1893 = 4 SF

2. Zeroes between non-zero numbers are always significant. Example: 209 = 3 SF 34007 = 5 SF

• 3. All final zeroes to the right of the decimal are significant. Example: 256. 90 = 5 SF 6, 220, 000. 780 = 10 SF 240. 519000 = 9 SF

4. Zeroes that act as placeholders are NOT significant. Example: 0. 06 = 1 SF 290 = 2 SF 982 400 = 4 SF 0. 0045100 = 5 SF

• 5. Counting numbers and defined constants have an infinite number of significant figures.

Rounding off numbers… • Suppose you have to find the density of a sample of Al with a mass of 382. 15 g and a volume of 145 ml. Your calculator would give you an answer of 2. 63551724. . . . • Your answer can not have any more significant figures than the data with the least # of SF. So then

382. 15 = 5 SF 145 = 3 SF So our answer can only have 3 SF 2. 63551724. . . . Must be reported as 2. 64 g/m. L

Addition and subtraction with SF When you add or subtract, your answer is based on the number that has the fewest number of digits to the right of the decimal

Ex. #1 14. 63 + 9. 009 +135. 2 158. 839 158. 8

Ex. #2 195. 336 + 46. 7788 242. 1148 242. 115
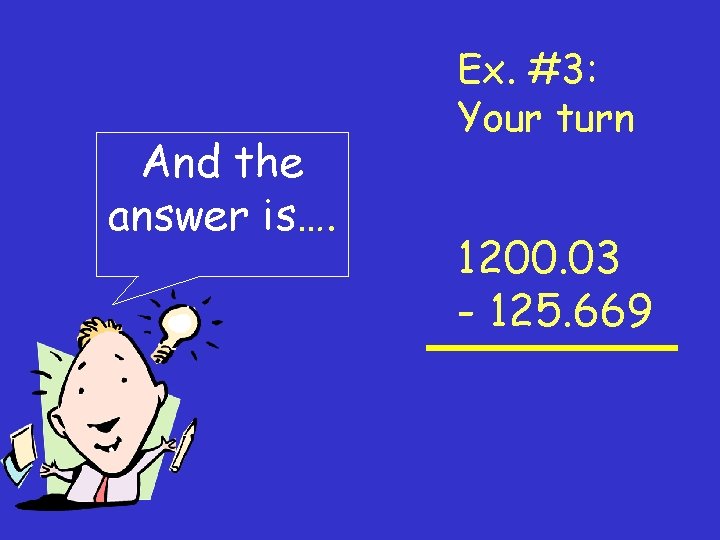
And the answer is…. Ex. #3: Your turn 1200. 03 - 125. 669

Answer: 1200. 03 - 125. 669 1074. 361 1074. 36

Pg. 41, Prac. Problems 35. a. ) b. ) c. ) 36. a. ) b. ) c. ) 142. 9 cm 768 kg 0. 1119 mg 12. 12 cm 2. 10 cm 2. 7 x 103 cm

Multiplying and dividing SF Remember that old rule about no chain is any stronger than it’s weakest link? No answer in multiplying and dividing can have more SF in it than any number in the actual problem

Ex. #1: 6. 220 x 12 (4 SF x 2 SF = 74. 64 = 2 SF) So 74. 64 (4 SF) 75 (2 SF)

Ex. #2: 9. 67 x 12 000 x 0. 9007= ? Answer

Answer 9. 67 x 12 000 x 0. 9007= ? 3 SF 2 SF 4 SF = 2 SF 104 517. 228 becomes 100 000* * Bar shows that the zero is significant and not just a place holder!

Ex. #3 1. 46 x 6 10 x 14. 566 x 0. 0230 63. 289 Answer

Answer #3 1. 46 x 106 x 14. 566 x 0. 0230 63. 289 3 SF x 5 SF x 3 SF/5 SF = 3 SF = 7 728. 4564. . . (etc) = 7 730

Pg. 42 37. a. b. c. d. 38. a. b. 78 12 2. 5 81. 1 2. 0 3. 00 c. 2. 00 d. 2. 9

Insignificant

End Chapter 2
- Slides: 73