Chapter 2 cont Fluid Statics Hydrostatic Forces Buoyancy

Chapter 2 (cont. ) Fluid Statics Hydrostatic Forces & Buoyancy

FLUID STATICS Deals with problems associated with fluid at rest. No relative motion between adjacent layers. Thus, no shear stress (tangential stress) to deform the fluid. Liquid – hydrostatics; Gas – aerostatics.

FLUID STATICS The only stress in fluid statics is normal stress (perpendicular to surface) • Normal stress is due to pressure (Pressure: gravity field-weight of fluid) • Variation of pressure is due only to the weight of the fluid → fluid statics is only relevant in presence of gravity fields. Applications: Floating or submerged bodies, water dams and gates, liquid storage tanks, etc.

HYDROSTATIC FORCES F=PA Only when the pressure distribution is uniform over the entire area of interest.

HYDROSTATIC FORCES What about the areas where the pressure is non-uniformly distributed ? ? FIND THE AVERAGE PRESSURE AND WHERE IT ACTS

HYDROSTATIC FORCES ON PLANE SURFACES Problem • To find the resultant force FR (magnitude) and its point of application (center of pressure) for non-uniformly distributed pressure. **Atmospheric pressure Patm can be neglected when it acts on both sides of the surface.

The Hoover Dam is an example of an arch-gravity dam. The Gathright Dam in Virginia is a rock-fill embankment dam.

The Grand Coulee Dam is an example of a solid gravity dam. Gordan Dam, Tasmania is an arch dam The Koshi Barrage dam

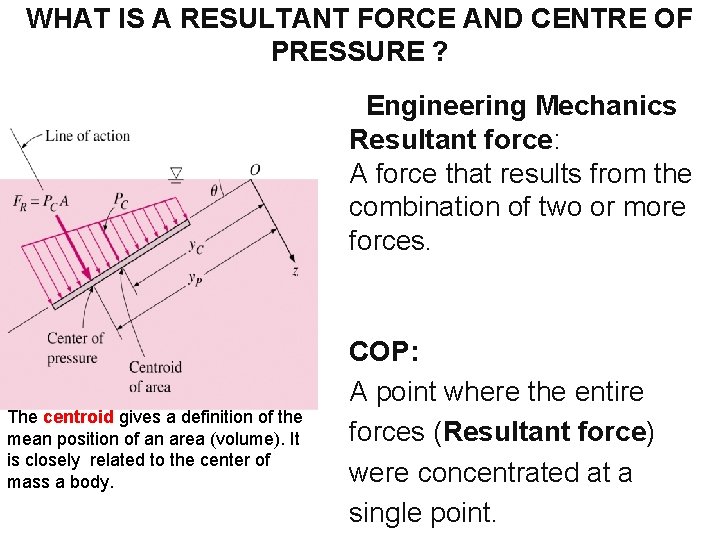
WHAT IS A RESULTANT FORCE AND CENTRE OF PRESSURE ? Engineering Mechanics Resultant force: A force that results from the combination of two or more forces. The centroid gives a definition of the mean position of an area (volume). It is closely related to the center of mass a body. COP: A point where the entire forces (Resultant force) were concentrated at a single point.

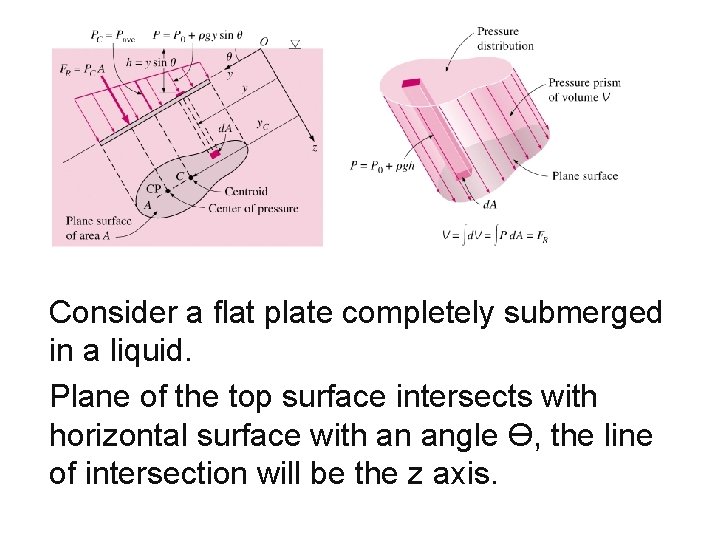
HOW TO DETERMINE THE RESULTANT FORCE Consider a flat plate completely submerged in a liquid. Plane of the top surface intersects with horizontal surface with an angle Ө, the line of intersection will be the z axis.

HOW TO DETERMINE THE RESULTANT FORCE, FR Absolute pressure at any point of the fluid, P = Po + ρgh, h = y sin Ө = Po + ρgy sin Ө, d. FR = Pd. A =∫ (Po + ρgy sin Ө)d. A = Po. A + ρg sin Ө ∫yd. A if Po, ρ, g and Ө are constant The 1 st moments of areas are the average displacement of an area about an axis of rotation. They are closely related to the centroid. **∫yd. A is the first moment of area with respect the z axis can be written as, yc A = ∫ yd. A where yc is the y coordinate of the centriod of area A measured from the z axis which passes through O FR = (Po + ρgyc sin Ө) A = (Po + ρghc) A = Pc. A=Pavg. A The magnitude of the resultant force, FR acting on a plane surface of a completely submerged plate in a homogeneous (constant density) fluid is = the product of the pressure Pc at the centroid of the surface and the area A of the surface.

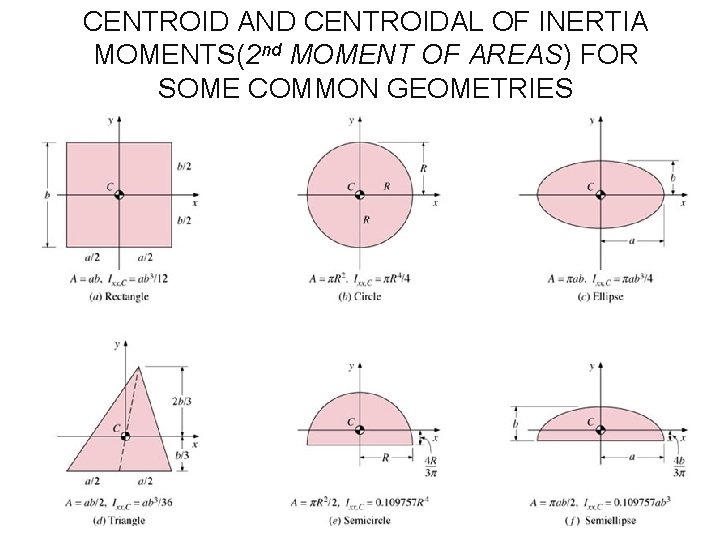
CENTROID AND CENTROIDAL OF INERTIA MOMENTS(2 nd MOMENT OF AREAS) FOR SOME COMMON GEOMETRIES

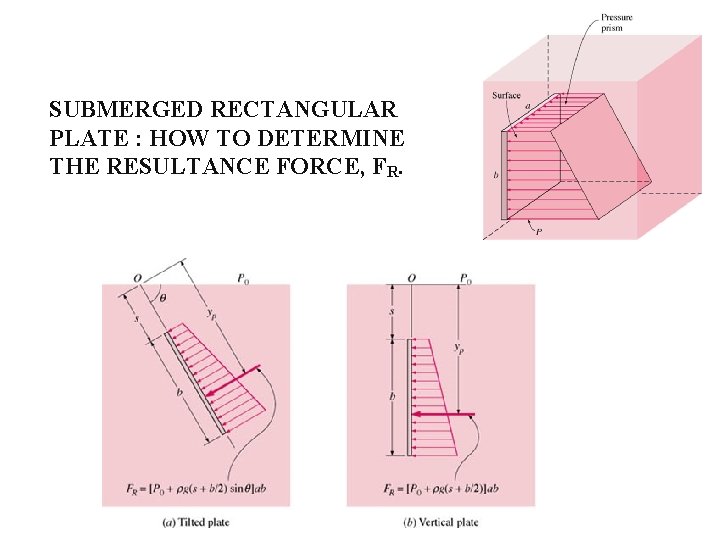
SUBMERGED RECTANGULAR PLATE : HOW TO DETERMINE THE RESULTANCE FORCE, FR.

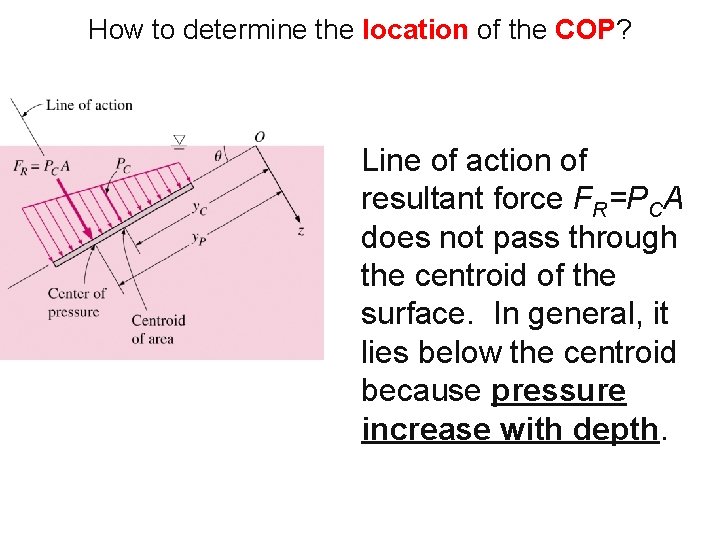
How to determine the location of the COP? Line of action of resultant force FR=PCA does not pass through the centroid of the surface. In general, it lies below the centroid because pressure increase with depth.

How to determine the location of the resultant force (Center of Pressure) ? The vertical location of the line of action is determined by equating the moment of the resultant force, FR to the moment of the distributed pressure force about the z-axis. Then, yp. FR = ∫A y. P d. A =∫A y(Po + ρgy sin Ө) d. A = Po ∫A y d. A + ρgsin Ө ∫A y 2 d. A = Poyc. A + ρgsin Ө Izz, o

The 2 nd moments of areas are the average (displacement)2 of an area about an axis of rotation. Has units of m 4 Izz, o = ∫y 2 d. A is actually the second moment of area (also called the area moment of inertia)about the z axis passing through point O.

Normally, the second moment of area is given about the axes passing through the centroid of the area. Therefore, we need parallel axis theorem to relate the Izz, o and Izz, c Therefore, If Po = 0(atmospheric pressure)

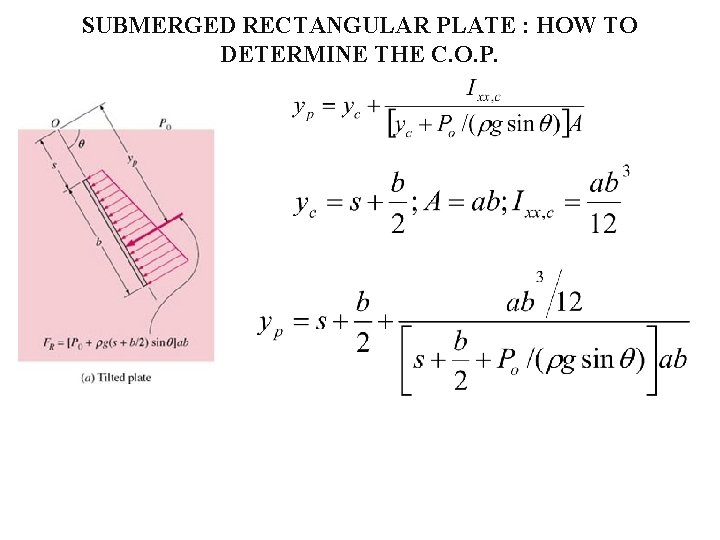
SUBMERGED RECTANGULAR PLATE : HOW TO DETERMINE THE C. O. P.

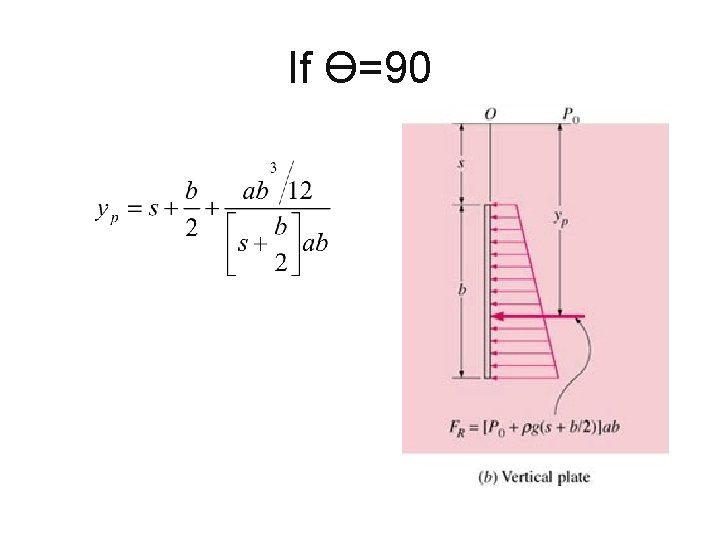
If Ө=90

Example : Calculate FR, C. O. P and discuss whether the driver can open the door or not. The moment acting on the mid point of the submerged door is 101. 3 k. N x 0. 5 m = 50. 6 k. Nm, which is 50 times of the moment the driver can possibly generate. CAN’T OPEN.

EXAMPLE A 5 -m-high, 5 -m-wide rectangular plate blocks the end of a 4 -m-deep freshwater channel, as shown below. The plate is hinged about a horizontal axis along its upper edge through a point A and is restrained from opening by a fixed ridge at point B. Determine the force exerted on the plate by the ridge.

A s=1 m FR h=4 m Fridge B Then the resultant hydrostatic force on each wall becomes The line of action of the force passes through the pressure center, which is 2 h/3 from the free surface, Taking the moment about point A and setting it equal to zero gives

Solving for Fridge and substituting, the reaction force is determined to be Discussion The difference between FR and Fridge is the force acting on the hinge at point A.

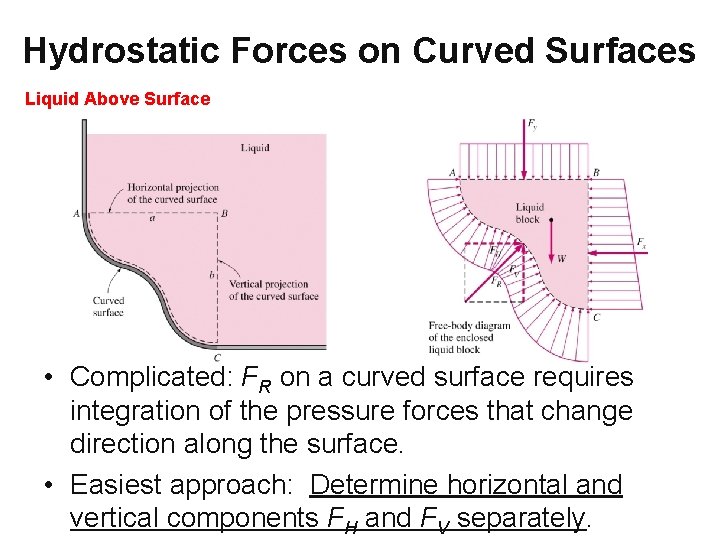
Hydrostatic Forces on Curved Surfaces Liquid Above Surface • Complicated: FR on a curved surface requires integration of the pressure forces that change direction along the surface. • Easiest approach: Determine horizontal and vertical components FH and FV separately.

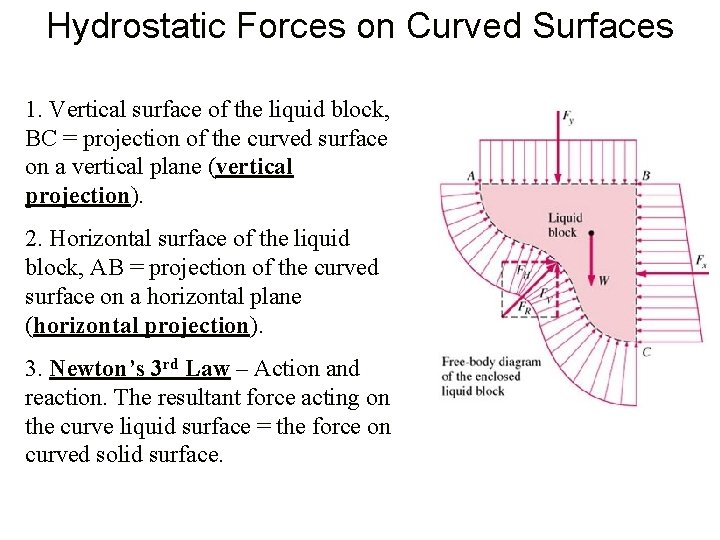
Hydrostatic Forces on Curved Surfaces 1. Vertical surface of the liquid block, BC = projection of the curved surface on a vertical plane (vertical projection). 2. Horizontal surface of the liquid block, AB = projection of the curved surface on a horizontal plane (horizontal projection). 3. Newton’s 3 rd Law – Action and reaction. The resultant force acting on the curve liquid surface = the force on curved solid surface.

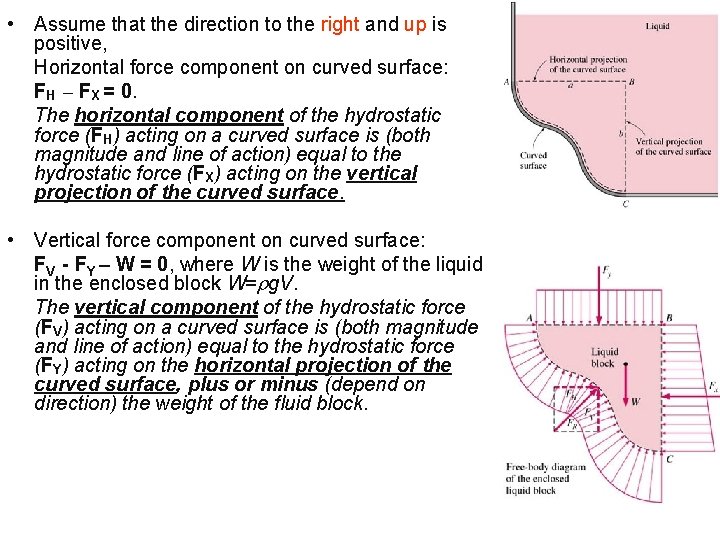
• Assume that the direction to the right and up is positive, Horizontal force component on curved surface: FH – FX = 0. The horizontal component of the hydrostatic force (FH) acting on a curved surface is (both magnitude and line of action) equal to the hydrostatic force (FX) acting on the vertical projection of the curved surface. • Vertical force component on curved surface: FV - FY – W = 0, where W is the weight of the liquid in the enclosed block W=rg. V. The vertical component of the hydrostatic force (FV) acting on a curved surface is (both magnitude and line of action) equal to the hydrostatic force (FY) acting on the horizontal projection of the curved surface, plus or minus (depend on direction) the weight of the fluid block.

Hydrostatic Forces on Curved Surfaces Magnitude of force FR=(FH 2+FV 2)1/2 Angle of force is a = tan-1(FV/FH)

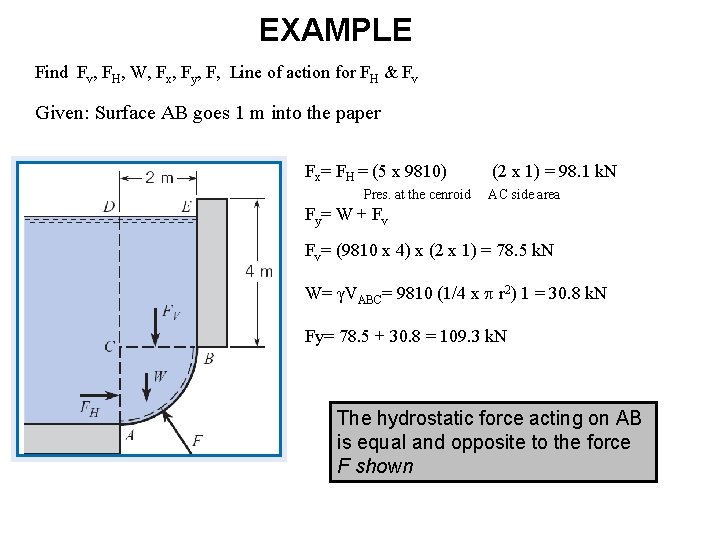
EXAMPLE Find Fv, FH, W, Fx, Fy, F, Line of action for FH & Fv Given: Surface AB goes 1 m into the paper Fx= FH = (5 x 9810) Pres. at the cenroid (2 x 1) = 98. 1 k. N AC side area Fy = W + F v Fv= (9810 x 4) x (2 x 1) = 78. 5 k. N W= γVABC= 9810 (1/4 x r 2) 1 = 30. 8 k. N Fy= 78. 5 + 30. 8 = 109. 3 k. N The hydrostatic force acting on AB is equal and opposite to the force F shown

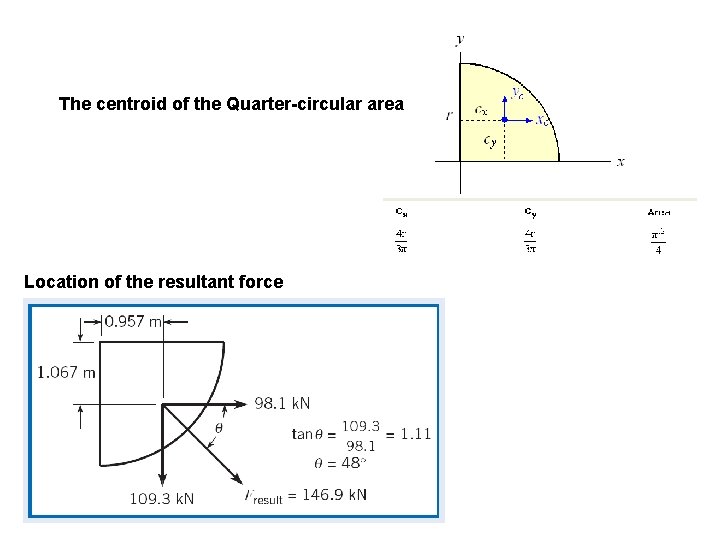
The centroid of the Quarter-circular area Location of the resultant force

BUOYANCY An objects lighter and weigh less in fluid compare to in an air. Fluid exerts an upward force on a body immersed in it. This force that tends to lift the body is called the buoyant force or the force of buoyancy.

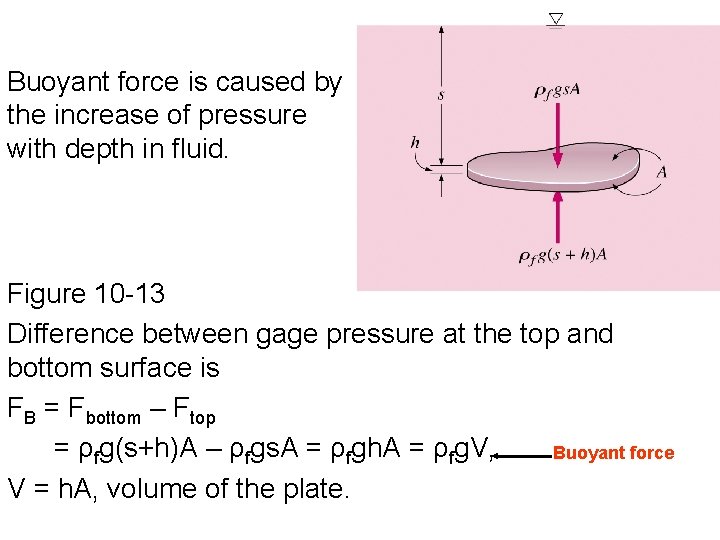
Buoyant force is caused by the increase of pressure with depth in fluid. Figure 10 -13 Difference between gage pressure at the top and bottom surface is FB = Fbottom – Ftop = ρfg(s+h)A – ρfgs. A = ρfgh. A = ρfg. V, Buoyant force V = h. A, volume of the plate.

We conclude that the buoyant force acting on the plate is equal to the weight of the liquid displaced by the plate.

Archimedes principal : The buoyant force acting on a body immersed in a fluid is equal to the weight of the fluid displaced by the body, and it acts upward through the centroid of the displaced volume. FB=ρfg. V Density of fluid

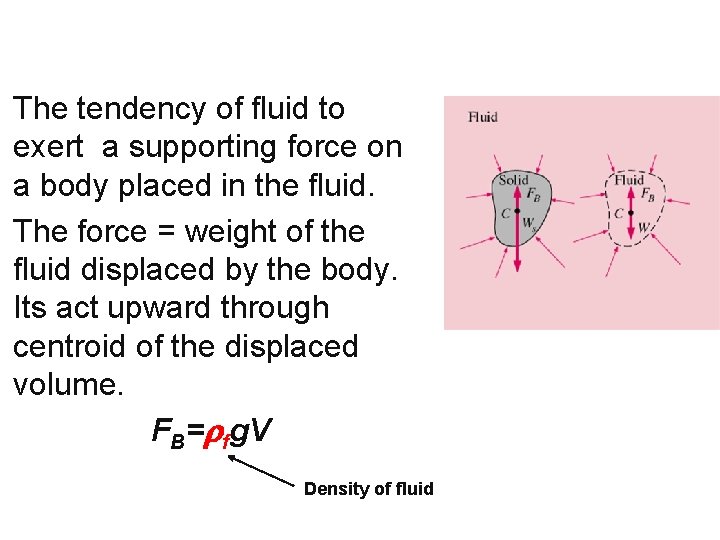
The tendency of fluid to exert a supporting force on a body placed in the fluid. The force = weight of the fluid displaced by the body. Its act upward through centroid of the displaced volume. FB=rfg. V Density of fluid

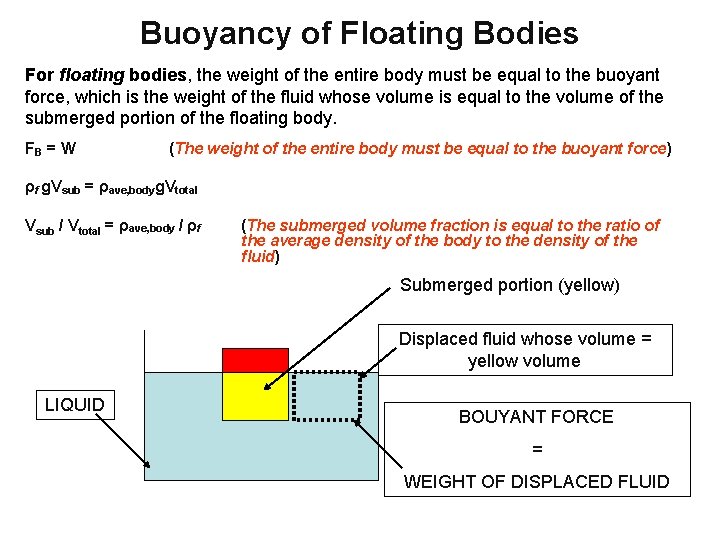
Buoyancy of Floating Bodies For floating bodies, the weight of the entire body must be equal to the buoyant force, which is the weight of the fluid whose volume is equal to the volume of the submerged portion of the floating body. FB = W (The weight of the entire body must be equal to the buoyant force) ρf g. Vsub = ρave, bodyg. Vtotal Vsub / Vtotal = ρave, body / ρf (The submerged volume fraction is equal to the ratio of the average density of the body to the density of the fluid) Submerged portion (yellow) Displaced fluid whose volume = yellow volume LIQUID BOUYANT FORCE = WEIGHT OF DISPLACED FLUID

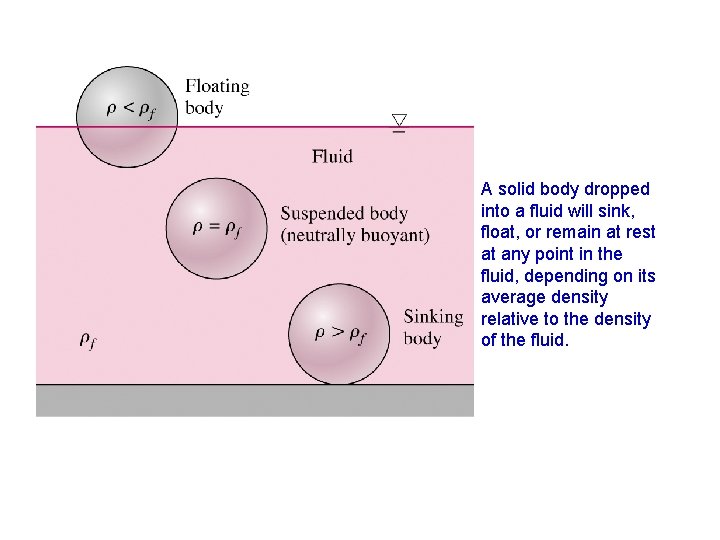
A solid body dropped into a fluid will sink, float, or remain at rest at any point in the fluid, depending on its average density relative to the density of the fluid.

A ship floats on the surface of sea water if the upward buoyancy force that it receives is great enough to overcome the downward force of its weight. A steel ship is hollow inside so that the overall density of the ship is less than that of sea water. The level a ship sinks in the sea depends on the buoyant force that acts on it. The deeper a ship sinks in the sea, the larger the volume of sea water that is displaced. Hence the buoyant force increases. The density of sea water varies with location. This will vary the level that the ship sinks in the sea. The denser the sea water, the larger the buoyant force. The ship will submerge deeper in fresh water than in sea water. The density of sea water varies with the region it is in and the season it sails. Therefore, most ships are marked with the Plimsoll line(waterline). The Plimsoll line is painted on ships to show the depth a ship should travel at. http: //scienceray. com/technology/transport/the-motion-of-vehicles-inwater/3/#ixzz 0 u. Oj. M

To float a submarine: a) water is forced out from the ballast tank with compressed air b) this decreases the density and weight of the submarine c) the buoyant force is larger than the weight of the submarine, causing the submarine to float. If the density of the submarine is the same as the density of the sea water, the depth of the submarine is maintained at one position. A submarine moves forward with the help of a propeller. Cross section of a vessel with a single ballast tank at the bottom. A submarine has a large ballast tank used to control the position and depth of the submarine from the surface of the sea. To sink a submarine: a) the ballast tank is filled with water b) this increases the density and weight of the submarine c) the submarine sinks when its weight is larger than the buoyant force.

BUOYANCY Buoyance force by air is so small, 0. 1 m 3, ρair = 1. 2 kg/m 3 , 1. 2 N. If mass = 80 kg, weigth = 788 N. Ignore the buoyancy, error is 0. 15%, so small. Rise of warm air – natural convection currents. The rise of hot air or Helium balloons, and air movements in the atmosphere.

EXAMPLE

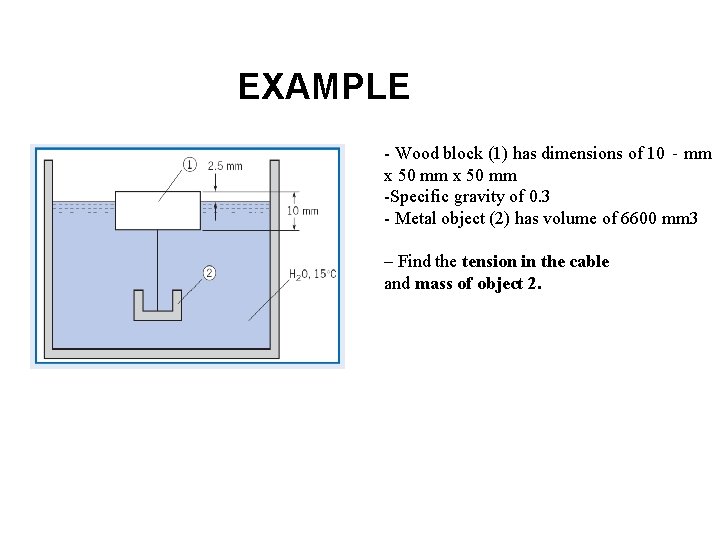
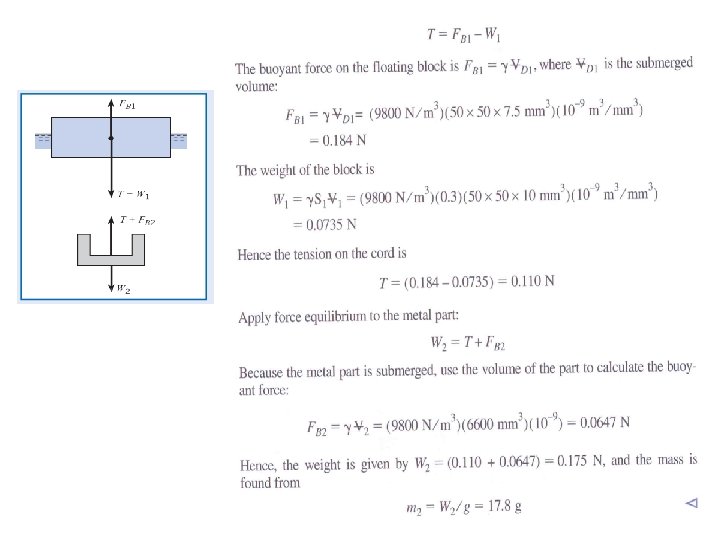
EXAMPLE - Wood block (1) has dimensions of 10‐mm x 50 mm -Specific gravity of 0. 3 - Metal object (2) has volume of 6600 mm 3 – Find the tension in the cable and mass of object 2.

EXAMPLE A rectangular pontoon has a width B of 6 m, a length l of 12 m, and a draught D of 1. 5 m in fresh water (density 1000 kg/m 3). Calculate : a) The weight of the pontoon b) Its draught in sea water (density 1025 kg/m 3) c) The load (in kilo. Newtons) that can be supported by the pontoon in fresh water if the maximum draught permissible is 2 m. Solution When the pontoon is floating in an unloaded condition, FB = weight of pontoon Since the up trust is equal to weight of the fluid displaced, Weight of pontoon = weight of fluid displaced, So,

a) In fresh water, and D=1. 5 m Therefore, Weight of pontoon, b) In the sea water, ; therefore Draught in sea water, c) For maximum draught of 2 m in fresh water, FB = weight of water displaced Load which can be supported = FB – weight of pontoon

EXAMPLE A raft is make by tying 5 empty steel barrels to a bamboo platform, as shown in next slide. The bamboo weigh 100 kg and each barrel is 0. 5 m in diameter, 1 m in length and has a mass of 15 kg. What is the maximum load in kilogram that the raft can carry before it sinks in fresh water? Data: Number of barrels = 5 d = 0. 5 m l = 1. 0 m Mass of each barrel = 15 kg Mass of bamboo = 100 kg

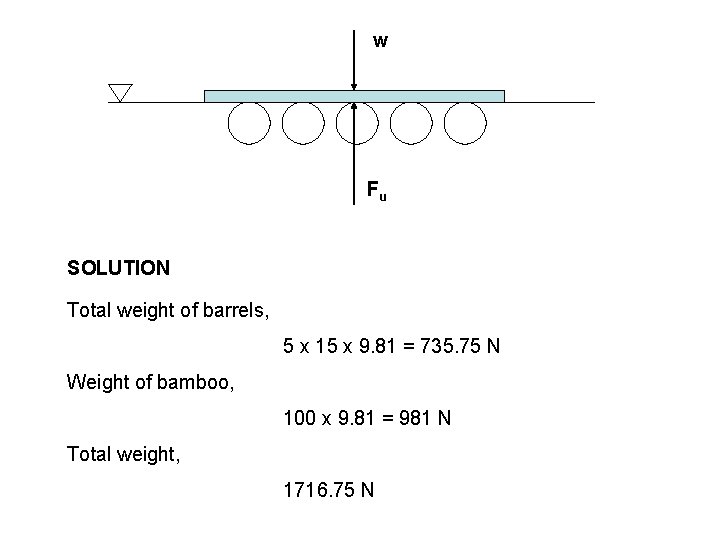
w Fu SOLUTION Total weight of barrels, 5 x 15 x 9. 81 = 735. 75 N Weight of bamboo, 100 x 9. 81 = 981 N Total weight, 1716. 75 N

The volume of water displaced by each barrel, The volume of water displaced by 5 barrels, 5 x 0. 196 = 0. 98 m 3 Therefore, FB = 0. 98 x 9. 81 x 1000 N = 9613. 8 N The nett upward force, FB – w = 9613. 8 – 1716. 75 = 7897 N Thus the mass that the raft can carry, 7897/9. 81 = 805 kg