Chapter 2 Concept learning Learning from examples Concept

Chapter 2 - Concept learning § Learning from examples § Concept Learning § General-to specific ordering of hypotheses § Version spaces and candidate elimination algorithm § Inductive bias § Simple approach n n Assumption: no noise Illustrates key concepts 1

Concept learning task § Given examples, learn a general concept (category) n subset of some general domain § E. g. , birds n boolean-valued function over the domain (characteristic function) § a function defined over all animals whose value is true for birds and false for every other animal § Definition n infer a boolean-valued function from samples of it (input, output) 2

Concept Learning § The problem is to learn a function mapping § § § examples into two classes: positive and negative. We are given a database of examples already classified as positive or negative. Concept learning: the process of inducing a function mapping input examples into a Boolean output. Examples: n n Classifying objects in astronomical images as stars or galaxies Classifying animals as vertebrates or invertebrates 3

Training Examples for Enjoy Sport Concept: ”days on which my friend Aldo enjoys his favourite water sports” Task: predict the value of ”Enjoy Sport” for an arbitrary day attributes based on the values of the other attributes Sky Temp Humid Wind Water Fore- Enjoy cast Sport Sunny Rainy Sunny Warm Cold Warm Cool Normal Strong High instance Strong High Strong Same Yes Change No Change Yes 4

Representing Hypothesis § Hypothesis h is a conjunction of constraints on attributes § Each constraint can be: n n n A specific value : e. g. Water=Warm A don’t care value : e. g. Water=? No value allowed (null hypothesis): e. g. Water=Ø § Example: hypothesis h Sky Temp Humid Wind Water Forecast < Sunny ? ? Strong ? Same > § Instance x satisfies hypothesis h n n all the constraints in h hold for x define h(x) = 1 5

Prototypical Concept Learning Task Given: § Instances X : Possible days decribed by the attributes Sky, Temp, Humidity, Wind, Water, Forecast § Target function c: Enjoy. Sport X {0, 1} § Hypotheses H: conjunction of literals e. g. < Sunny ? ? Strong ? Same > § Training examples D : positive and negative examples of the target function: <x 1, c(x 1)>, …, <xn, c(xn)> Determine: § A hypothesis h in H such that h(x)=c(x) for all x in D. 6

Inductive Learning Hypothesis § All we know of c are the examples § Best we can do is to produce a h consistent with example data § Any hypothesis found to approximate the target function well over the training examples, will also approximate the target function well over the unobserved examples. n fundamental assumption in inductive learning 7

Concept learning as search § H = search space n find h best fitting to D § Selection of representation defines search space n size of space (syntactic/semantic) § Efficient search in very large (or infinite) spaces for best h 8

# of Instances, Concepts, Hypo. s § § § Sky: Sunny, Cloudy, Rainy Air. Temp: Warm, Cold Humidity: Normal, High Wind: Strong, Weak Water: Warm, Cold Forecast: Same, Change #distinct instances : 3*2*2*2 = 96 #distinct concepts : 296 #syntactically distinct hypotheses : 5*4*4*4=5120 #semantically distinct hypotheses : 1+4*3*3*3=973 9

General-to-Specific order § Useful structure n n n organize the search process exists for any concept learning task search possible without enumerating all members of H (may be infinite) § A concept hj is more general than or equal to hk (written hj hk) if and only if x X : [ (hk(x) = 1) (hj(x) = 1)] 10

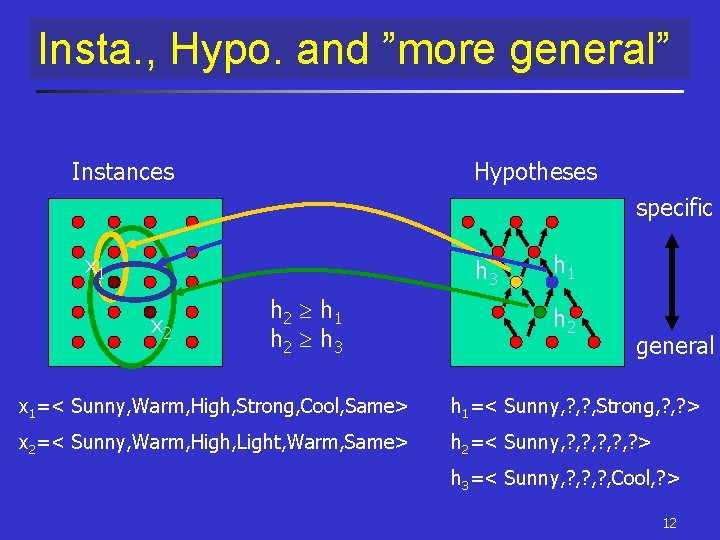
General to Specific Order § Consider two hypotheses: h 1=< Sunny, ? , Strong, ? > n h 2=< Sunny, ? , ? , ? > § Set of instances covered by h 1 and h 2: n n n h 2 imposes fewer constraints than h 1 and therefore classifies more instances x as positive. h 2 is more general than h 1 or h 2 h 1 § The relation imposes a partial order over the hypothesis space H that is n independent of c! n utilized by many concept learning methods. 11

Insta. , Hypo. and ”more general” Instances Hypotheses specific x 1 h 3 x 2 h 2 h 1 h 2 h 3 h 1 h 2 general x 1=< Sunny, Warm, High, Strong, Cool, Same> h 1=< Sunny, ? , Strong, ? > x 2=< Sunny, Warm, High, Light, Warm, Same> h 2=< Sunny, ? , ? , ? > h 3=< Sunny, ? , ? , Cool, ? > 12

Find-S algorithm § Example of using the ordering n n begin: the most specific member of H generalize it whenever h(x) = 0 and c(x) = 1 (examples) § Ignores negative examples n no problem assuming that § H contains a description of c and § D has no noise 13

Find-S Algorithm 1. Initialize h to the most specific hypothesis in H 2. For each positive training instance x n For each attribute constraint ai in h If the constraint ai in h is satisfied by x then do nothing else replace ai in h by the next more general constraint that is satisfied by x 3. Output hypothesis h 14

Hypoth. Space Search by Find-S Instances x 3 Hypotheses h 0 x 1 x 2 x 4 specific h 1 h 2, 3 h 4 general x 1=<Sunny, Warm, Normal, Strong, Warm, Same>+ h 0=< Ø, Ø, Ø, > h 1=< Sunny, Warm, Normal, Strong, Warm, Same> x 2=<Sunny, Warm, High, Strong, Warm, Same>+ h 2, 3=< Sunny, Warm, ? , x 3=<Rainy, Cold, High, Strong, Warm, Change> Strong, Warm, Same> x 4=<Sunny, Warm, High, Strong, Cool, Change> + h 4=< Sunny, Warm, ? , Strong, ? > 15

Find-S – Black board example § Size = large/small, Color = red/white/blue and Shape = cube/brick/round § Examples n n n Positive: obj(small, red, round) Positive: obj(small, white, round) Positive: obj(large, white, round) § What does Find-S find? § What if we add the following negative example ? n Negative: obj(large, blue, cube) § What if we add the following negative example ? n Negative: obj(large, blue, round) 16

Properties of Find-S § For Hypothesis space described by conjunctions of constraints, Find-S will output the most specific hypothesis within H that is consistent with the positve training examples § The output hypothesis will also be consistent with the negative examples, provided the target concept is contained in H. 17

Complaints about Find-S § Can’t tell if the learner has converged to the target concept, in the sense that it is unable to determine whether it has found the only hypothesis consistent with the training examples. § Can’t tell when training data is inconsistent, as it ignores negative training examples. § Why prefer the most specific hypothesis? § ‘most specific’ is not always unique. n Find-S cannot backtrack! 18

Version Space and Cand. Elimi. § Another learning approach n n outputs a description of all members of H that are consistent with D possible without enumerating members of H (ordering!) suffers from noise useful framework for introducing many fundamental issues of ML 19

Version Spaces § A hypothesis h is consistent with a set of training examples D of target concept if and only if h(x)=c(x) for each training example <x, c(x)> in D. n Consistent(h, D) : = <x, c(x)> D h(x)=c(x) § The version space, VSH, D , with respect to hypothesis space H, and training set D, is the subset of all hypotheses in H consistent with all training examples: n VSH, D = {h H | Consistent(h, D) } 20

Elimination algorithms § List-then-Eliminate § list every hypothesis in H § at each example, remove inconsistent hypo § output the list of surviving hypotheses something to start with n ineffective § Candidate elimination n same principle n more compact representation n maintain most specific and most general elements of VS(H, D) n 21

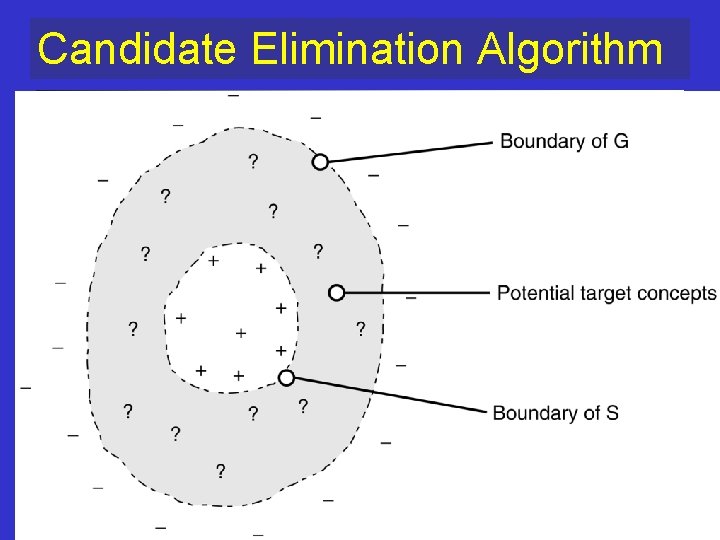
Representing Version Spaces § The general boundary, G, of version space VSH, D is the set of maximally general members. § The specific boundary, S, of version space VSH, D is the set of maximally specific members. § Every member of the version space lies between these boundaries VSH, D = {h H| ( s S) ( g G) (g h s) where x y means x is more general or equal than y 22

Example Version Space S: {<Sunny, Warm, ? , Strong, ? >} <Sunny, ? , Strong, ? > G: x 1 x 2 x 3 x 4 <Sunny, Warm, ? , ? > <? , Warm, ? , Strong, ? > {<Sunny, ? , ? , ? >, <? , Warm, ? , ? >, } = = <Sunny <Rainy <Sunny Warm Normal Strong Warm Same> + Warm High Strong Warm Same> + Cold High Strong Warm Change> Warm High Strong Cool Change> + 23

Representation theorem § For any n n set of instances X set H of boolean-valued hypotheses over X target concept c: X -> {0, 1} set of pairs <x, c(x)> D § VS(H, D) = {h | g >= h >= s} n where g & s range over G & S 24

Candidate Elimination Algorithm G maximally general hypotheses in H S maximally specific hypotheses in H For each training example d=<x, c(x)> If d is a positive example Remove from G any hypothesis that is inconsistent with d For each hypothesis s in S that is not consistent with d § remove s from S. § Add to S all minimal generalizations h of s such that n n h consistent with d Some member of G is more general than h § Remove from S any hypothesis that is more general than another hypothesis in S 25

Candidate Elimination Algorithm If d is a negative example Remove from S any hypothesis that is inconsistent with d For each hypothesis g in G that is not consistent with d § remove g from G. § Add to G all minimal specializations h of g such that n n h consistent with d Some member of S is more specific than h § Remove from G any hypothesis that is less general than another hypothesis in G 26

Candidate Elimination Algorithm 27

Example Candidate Elimination S: {< , , , >} G: {<? , ? , ? , ? >} x 1 = <Sunny Warm Normal Strong Warm Same> + S: {< G: Sunny Warm Normal Strong Warm Same >} {<? , ? , ? , ? >} x 2 = <Sunny Warm High Strong Warm Same> + S: G: {< Sunny Warm ? Strong Warm Same >} {<? , ? , ? , ? >} 28

Example Candidate Elimination. . S: {< G: Sunny Warm ? Strong Warm Same >} {<? , ? , ? , ? >} x 3 = <Rainy Cold High S: G: {< Strong Warm Change> - Sunny Warm ? Strong Warm Same >} {<Sunny, ? , ? , ? >, <? , Warm, ? , ? >, <? , ? , ? , Same>} x 4 = <Sunny Warm High Strong Cool Change> + S: {< Sunny Warm ? Strong ? ? >} G: {<Sunny, ? , ? , ? >, <? , Warm, ? , ? > } 29

Example Candidate Elimination. . S: {<Sunny, Warm, ? , Strong, ? >} <Sunny, ? , Strong, ? > G: x 1 x 2 x 3 x 4 <Sunny, Warm, ? , ? > <? , Warm, ? , Strong, ? > {<Sunny, ? , ? , ? >, <? , Warm, ? , ? >, } = = <Sunny <Rainy <Sunny Warm Normal Strong Warm Same> + Warm High Strong Warm Same> + Cold High Strong Warm Change> Warm High Strong Cool Change> + 30

Cand. Elim. – Black board example § Size = large/small, Color = red/white/blue and Shape = cube/brick/round § Examples n n Positive (+): obj(small, red, round) Negative (-): obj(small, blue, round) Positive (+): obj(large, red, round) Negative (-): obj(large, red, cube) § What does Candidate Elimination find? 31

Remarks on VS & CE § Converges to correct h? n n If no errors, H rich enough: yes exact: G = S and both singletons § Effect of errors (noise) n n example 2 negative -> CE removes the correct target from VS! detection: VS gets empty § Similarly, VS gets empty when c can not be represented (e. g. disjunctions) 32

Classification of New Data S: {<Sunny, Warm, ? , Strong, ? >} <Sunny, ? , Strong, ? > G: x 5 x 6 x 7 x 8 <Sunny, Warm, ? , ? > <? , Warm, ? , Strong, ? > {<Sunny, ? , ? , ? >, <? , Warm, ? , ? >, } = = <Sunny <Rainy <Sunny Warm Normal Strong Cool Change> + 6/0 Cold Normal Light Warm Same> - 0/6 Warm Normal Light Warm Same> ? 3/3 Cold Normal Strong Warm Same> ? 2/4 33

How to use partially learned concepts? § Classification with ambiguous VS n n n h(x) = 0/1 for every h in VS: ok enough to check with G (0) & S (1) 3 rd example: 50% support for both 4 th: 66% support for 0 majority vote + confidence? Ok if all h are equally likely 34

What example next? § Three settings for learning: n n n Tasks are generated by a random process outside the learner The learner can pose queries to be classified by a teacher The learner explores its surroundings autonomously (conducts an experiment) § What to ask/check as next example/query? n n Is there a good general strategy? Should attempt to discriminate among the alternatives in VS 35

What to ask. . . § Discriminating example n n c(x) = 1: S will generalize c(x) = 0: G will specialize § Optimal choice halves VS n n x satisfies half of VS members for example, § <Sunny, warm, Normal, Light, Warm, Same> n n not possible to generate one in general if we are able to do this, we can find an optimal hypothesis in log 2 |VS| steps 36

Inductive Leap + <Sunny Warm Normal Strong Cool Change> + <Sunny Warm Normal Light Warm Same> S : <Sunny Warm Normal ? ? ? > • How can we justify to classify the new example as + <Sunny Warm Normal Strong Warm Same> Bias: We assume that the hypothesis space H contains the target concept c. In other words that c can be described by a conjunction of literals. 37

Biased hypothesis space § Assure H contains c n n make H general enough what if it’s not? § Example case n max specific h consistent with x 1 & x 2 (+) is too general for x 3 (-) See next slide § x 1 = <Sunny Warm Normal Strong Cool Change> + § x 2 = <Cloudy Warm Normal Strong Cool Change> + § x 3 = <Rainy Warm Normal Strong Cool Change> - n reason: we have biased the learner to consider only conjunctions 38

Biased Hypothesis Space § Our hypothesis space is unable to represent a simple disjunctive target concept : (Sky=Sunny) v (Sky=Cloudy) x 1 = <Sunny Warm Normal Strong Cool Change> + x 2 = <Cloudy Warm Normal Strong Cool Change> + S : { <? , Warm, Normal, Strong, Cool, Change> } x 3 = <Rainy Warm Normal Strong, Cool, Change> S : {} 39

Unbiased Learner § Idea: Choose H that expresses every teachable concept, that means H is the set of all possible subsets of X called the power set P(X) § |X|=96, |P(X)|=296 ~ 1028 distinct concepts (too large!) § H = disjunctions, conjunctions, negations n e. g. <Sunny Warm Normal ? ? ? > v <? ? ? Change> § H surely contains the target concept. n n n Sky = Sunny or Sky = Cloudy eliminates problems of expressibility BUT, also eliminates the ability to generalize! 40

Unbiased Learner § Assume we have positive examples (x 1, x 2, x 3) and negative examples (x 4, x 5) n n S : { (x 1 v x 2 v x 3) } G : { (x 4 v x 5) } § The only examples that are classified are the training examples themselves. n n Each unobserved instance will be classified positive by precisely half the hypothesis in VS For every concept classifying x positively, there is another concept that differs only on x, classifies x negatively. § That’s, in order to learn the target concept one would have to present every single instance in X as a training example. 41

Futility of Bias-Free Learning § If n learner makes no a priori assumptions on the target concept § Then n it has no rational basis for classifying any unseen instances § Inductive bias = prior assumptions § Inductive bias is the preference for a hypothesis space H and a search mechanism over H. 42

Inductive Bias § Consider n n Concept learning algorithm L Instances X, target concept c Training examples Dc={<x, c(x)>} Let L(xi, Dc ) denote the classification assigned to instance xi by L after training on Dc. § Definition: The inductive bias of L is any minimal set of assertions B such that for any target concept c and corresponding training data Dc ( xi X)[B Dc xi] |-- L(xi, Dc) Where A |-- B means that A logically entails B. 43

Inductive and Deductive Systems training examples candidate elimination algorithm new instance training examples classification of new instance or don’t know using hypothesis space H equivalent deductive system new instance theorem prover classification of new instance or don’t know assertion ”H contains target concept” 44

Schematic summary § Top: inductive system n built-in (implicit) bias § Bottom: deductive system n n n explicit bias non-procedural way for characterizing learning systems allows comparisons of different learning algorithms 45

Three learners & their biases § Rote learner: no bias § Candidate Elimination n c is (representable) in H § Find-S n The hypothesis space contains the target concept and all instances are negative instances unless the opposite is entailed by its other knowledge. § c is the most specific consistent hypotheses of H 46

Summary § The input space is the space of all examples; the § § output space is the space of all classes. A hypothesis maps examples into classes. We want a hypothesis close to target concept c. The General-to specific ordering establishes a natural partial ordering over the hypothesis space. One can exploit this ordering to move along the corresponding lattice. 47

Summary § The candidate elimination algorithm exploits the general-specific ordering of hypotheses to find all hypotheses consistent with the training data. § The version space contains all consistent hypotheses and is simply represented by two lists: S and G. § Candidate elimination algorithm is not robust to noise and assumes the target concept is included in the hypothesis space. § Any inductive algorithm needs some assumptions about the hypothesis space, otherwise it would be impossible to perform predictions. 48