Chapter 2 Business Efficiency Hamiltonian Circuit Visiting Vertices

Chapter 2: Business Efficiency Hamiltonian Circuit • Visiting Vertices – In some graph theory problems, it is only necessary to visit specific locations (using the travel routes, or streets available). – Problem: Find an efficient route along distinct edges of a graph that visits each vertex only once in a simple circuit. 1

Chapter 2: Business Efficiency Hamiltonian Circuit Applications: n Salesman visiting particular cities n Delivering mail to drop-off boxes n Route taken by a snowplow n Pharmaceutical representative visiting doctors 2

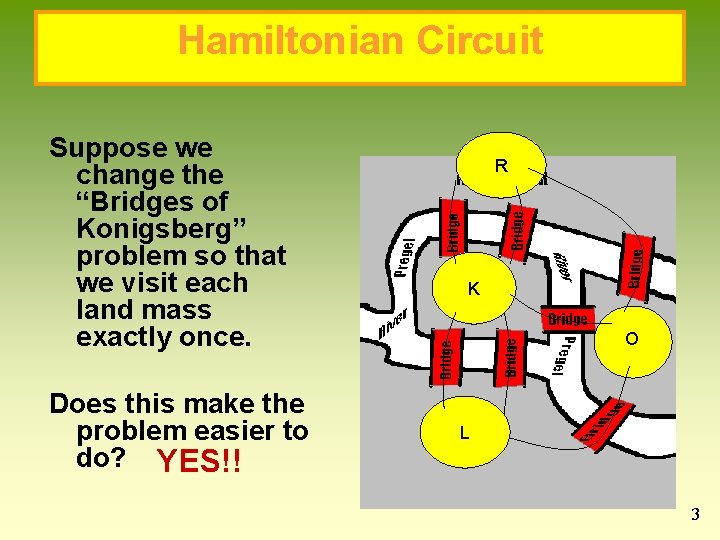
Hamiltonian Circuit Suppose we change the “Bridges of Konigsberg” problem so that we visit each land mass exactly once. Does this make the problem easier to do? YES!! R K O L 3

Chapter 2: Hamilton Circuits Outline/Learning Objectives • To identify and model Hamilton circuit problems. • To use the following algorithms to determine the optimal route for a Traveling Salesman Problem. – Nearest Neighbor and Sorted Edges Algorithms – Minimum-Cost Spanning Trees • Kruskal’s Algorithm

Sir William Rowan Hamilton (1805 – 1865) He was a renowned Irish mathematician and astronomer. He was a child prodigy. He could read English, Hebrew, Greek, and Latin by the time he was 4 yrs old. He became Professor of Astronomy at Trinity College in Dublin, Ireland when he was 23 yrs old. 5

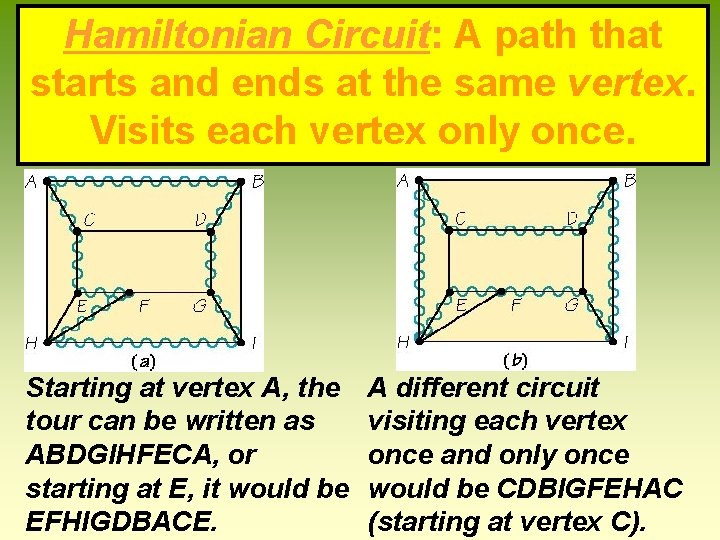
Hamiltonian Circuit: A path that starts and ends at the same vertex. Visits each vertex only once. Starting at vertex A, the tour can be written as ABDGIHFECA, or starting at E, it would be EFHIGDBACE. A different circuit visiting each vertex once and only once would be CDBIGFEHAC (starting at vertex C).

Hamiltonian Circuit: - Circuits can start at any location. Notice that we don’t care that we don’t use all the edges. Use wiggly edges to show the circuit. Unfortunately, there are no theorems that tell us whether or not a graph has a Hamilton Circuit. Starting at vertex A, the tour can be written as ABDGIHFECA, or starting at E, it would be EFHIGDBACE. A different circuit visiting each vertex once and only once would be CDBIGFEHAC (starting at vertex C). 7

Hamiltonian Circuit vs. Euler Circuits Hamiltonian circuit – A path (shown by wiggly edges) that starts at a vertex of a graph and visits each vertex once and only once, returning to where it started. Euler circuit – A circuit that traverses each edge of a graph exactly once and starts and stops at the same vertex. 8

Hamiltonian Circuit vs. Euler Circuits • Similarities – Both forbid re-use. • Hamiltonian didn’t reuse vertices. • Euler didn’t reuse edges. • Differences – Hamiltonian is a circuit of vertices. – Euler is a circuit of edges. – Euler graphs are easy to spot (connectedness and even valence). – Hamiltonian circuits are NOT as easy to determine upon inspection. 9

Hamiltonian Circuit vs. Euler Circuits Find both an Euler and Hamilton Circuit A B C D G F E Hamilton: one possible solution: AGFECDBA Euler: B and D have odd valences. Therefore, there is NO Euler Circuit. 10

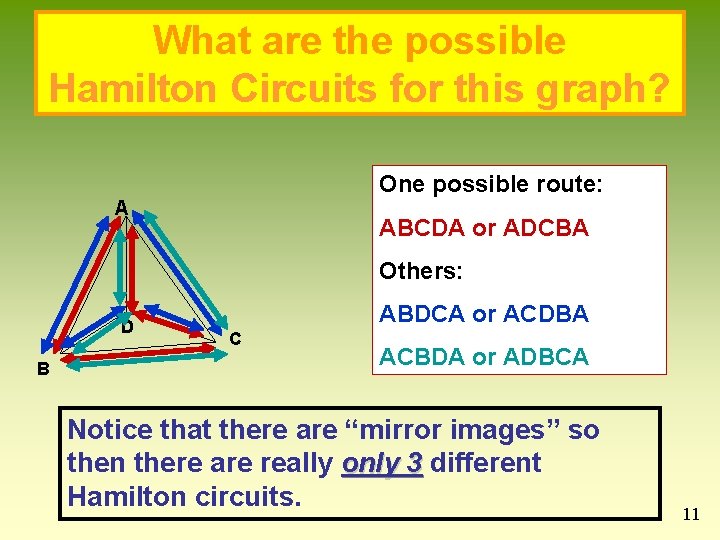
What are the possible Hamilton Circuits for this graph? One possible route: A ABCDA or ADCBA Others: D B ABDCA or ACDBA C ACBDA or ADBCA Notice that there are “mirror images” so then there are really only 3 different Hamilton circuits. 11

What are the possible Hamilton Circuits for this graph if we start at A? A ABCDA or ADCBA ABDCA or ACDBA ACBDA or ADBCA D B C When we start at A how many ways can we travel: 3 (B, D, C) If we choose B, how many ways can we travel: 2 (D, C) If we choose D, how many ways can we travel: 1 (C) This means that we can have 3 x 2 x 1 possible different combinations. This can be written as 3! How does 3 relate to the number of vertices? One less than 3! = 6, but half were mirror images so 3!/2 = 3 would be the correct amount of unique Hamilton circuits. 12

Unique Hamilton Circuits • Principle of Counting for Hamiltonian Circuits – For a complete graph of n vertices, there are (n - 1)! possible routes. – Half of these routes are repeats, the result is: Possible unique Hamiltonian circuits are (n - 1)! / 2 Complete graph – A graph in which every pair of vertices is joined by an edge. n Fundamental Principle of Counting If there a ways of choosing one thing, b ways of choosing a second after the first is chosen, c ways of choosing a third after the second is chosen…, and so on…, and z ways of choosing the last item after the earlier choices, then the total number of choice patterns is a × b × c × … × z. Example: Jack has 9 shirts and 4 pairs of pants. He can wear 9 × 4 = 36 shirt-pant outfits. 13

How many unique Hamilton circuits are there and name one. 5 vertices so there are 4! Hamilton circuits. C B D 4! = 24 circuits 24/2 = 12 A E unique circuits (Be happy. I will only ask you to find one!) Example: ABCDEA 14

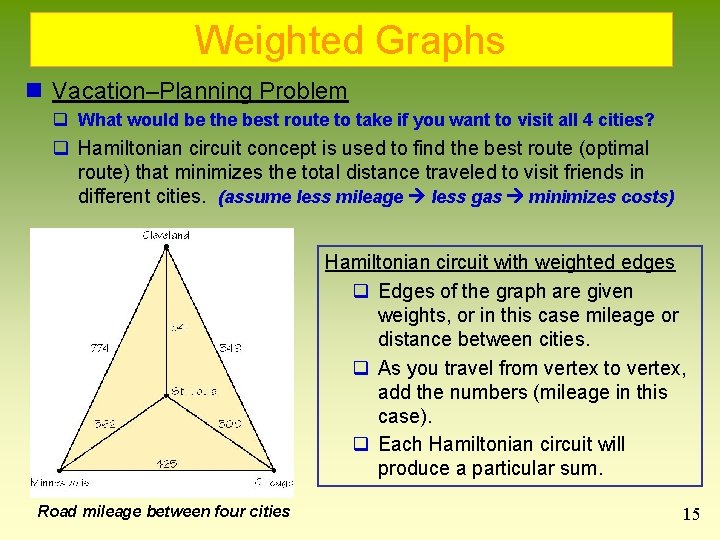
Weighted Graphs n Vacation–Planning Problem q What would be the best route to take if you want to visit all 4 cities? q Hamiltonian circuit concept is used to find the best route (optimal route) that minimizes the total distance traveled to visit friends in different cities. (assume less mileage less gas minimizes costs) Hamiltonian circuit with weighted edges q Edges of the graph are given weights, or in this case mileage or distance between cities. q As you travel from vertex to vertex, add the numbers (mileage in this case). q Each Hamiltonian circuit will produce a particular sum. Road mileage between four cities 15

Definitions Ø Weighted graph – has numbers assigned to an edge that can be thought of as cost, distance, or time. Ø Optimal solution – when a problem has various solutions and you pick the best solution for you. Ø Algorithm – A step-by-step description of how to solve a problem. Heuristic Algorithm – A “fast” method that doesn’t guarantee an optimal answer.

Traveling Salesman Problem (TSP) • Weighted Graphs where the number of vertices in a complete graph are very large. • Difficult to solve Hamiltonian circuits. This problem originated from a salesman determining his trip that minimizes costs (less mileage) as he visits the cities in a sales territory, starting and ending the trip in the same city. • Many applications today: • • • bus schedules mail drop-offs to post offices Candy machine coin pick-up routes UPS Running phone lines or cable Water lines 17

Traveling Salesman Problem (TSP) How can the TSP be solved? • Computer program can find optimal route (not always practical). • Exhaustive search called Brute Force Algorithm (Trees can be used) • Heuristic methods can be used to find a “fast” answer, but does not guarantee that it is always the optimal answer. – Nearest Neighbor Algorithm (NNA) – Sorted Edges Algorithm (also known as “Cheapest Link”) – Kruskal’s Algorithm (Minimum Spanning Trees) 18

TSP Strategies for complete graphs 1) Brute Force Algorithm – optimal algorithm that always works but inefficient. Creates a Hamilton Circuit. 2) Nearest-Neighbor Algorithm (NNA) – not optimal but efficient. Creates a Hamilton Circuit. 3) Sorted-Edges Algorithm - not optimal but efficient. Creates a Hamilton Circuit. 4) Kruskal’s Algorithm and Minimum Cost Spanning Trees - not optimal but efficient. Does NOT create a Hamilton Circuit. 19

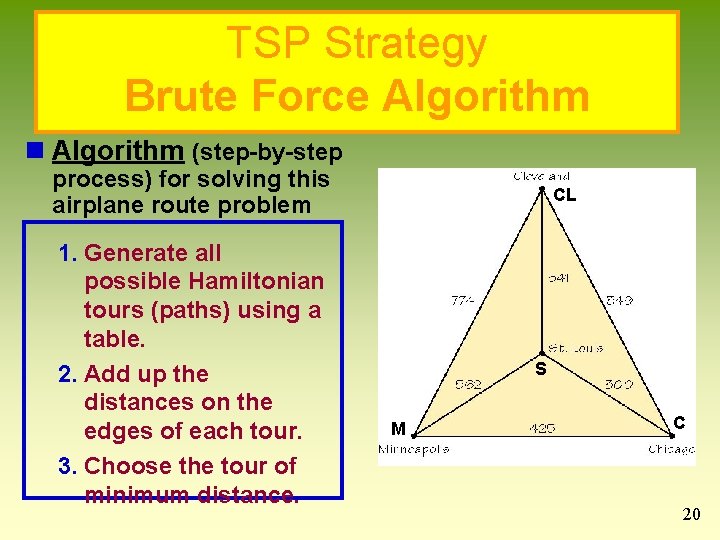
TSP Strategy Brute Force Algorithm n Algorithm (step-by-step process) for solving this airplane route problem 1. Generate all possible Hamiltonian tours (paths) using a table. 2. Add up the distances on the edges of each tour. 3. Choose the tour of minimum distance. CL S M C 20

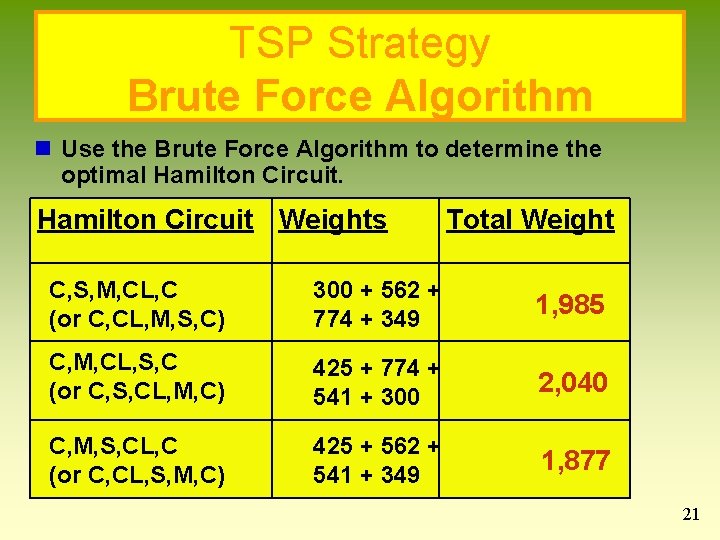
TSP Strategy Brute Force Algorithm n Use the Brute Force Algorithm to determine the optimal Hamilton Circuit Weights Total Weight C, S, M, CL, C (or C, CL, M, S, C) 300 + 562 + 774 + 349 1, 985 C, M, CL, S, C (or C, S, CL, M, C) 425 + 774 + 541 + 300 2, 040 C, M, S, CL, C (or C, CL, S, M, C) 425 + 562 + 541 + 349 1, 877 21

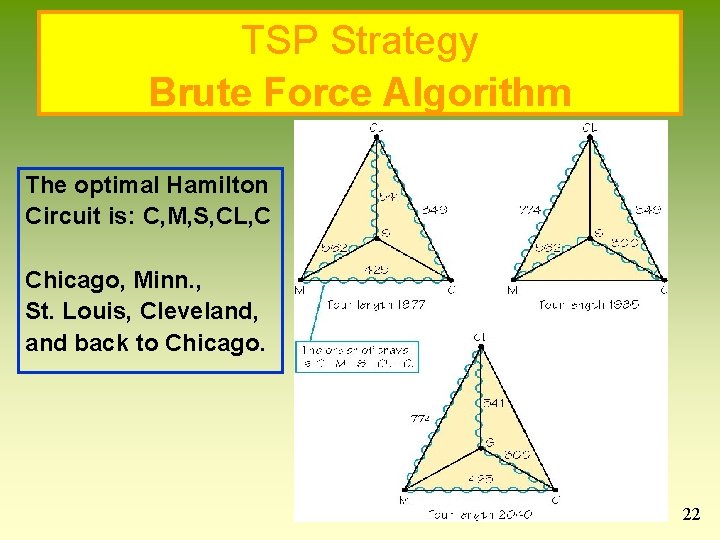
TSP Strategy Brute Force Algorithm The optimal Hamilton Circuit is: C, M, S, CL, C Chicago, Minn. , St. Louis, Cleveland, and back to Chicago. 22

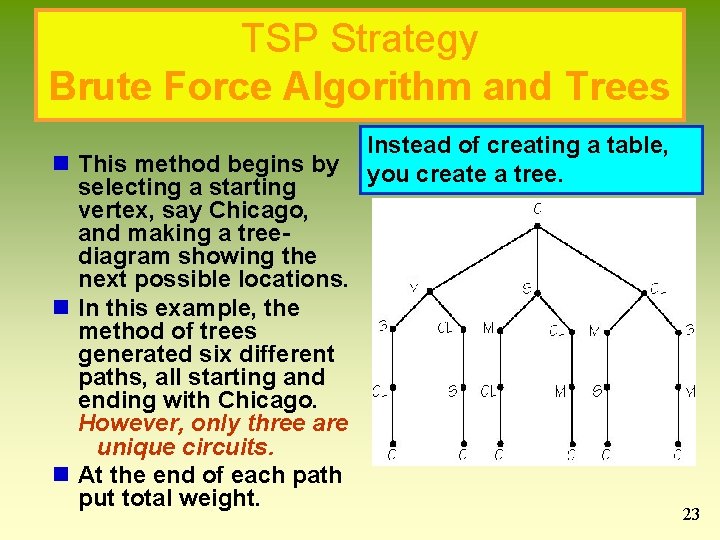
TSP Strategy Brute Force Algorithm and Trees n This method begins by selecting a starting vertex, say Chicago, and making a treediagram showing the next possible locations. n In this example, the method of trees generated six different paths, all starting and ending with Chicago. However, only three are unique circuits. n At the end of each path put total weight. Instead of creating a table, you create a tree. 23

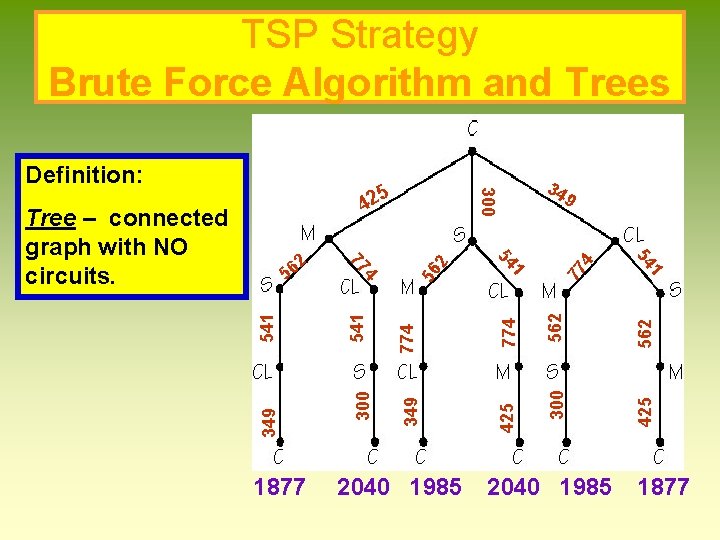
TSP Strategy Brute Force Algorithm and Trees 4 562 425 77 562 300 774 56 774 349 541 300 2040 1985 1 54 349 9 1 54 4 1877 77 2 56 2 4 Tree – connected graph with NO circuits. 34 300 25 425 Definition: 2040 1985 1877

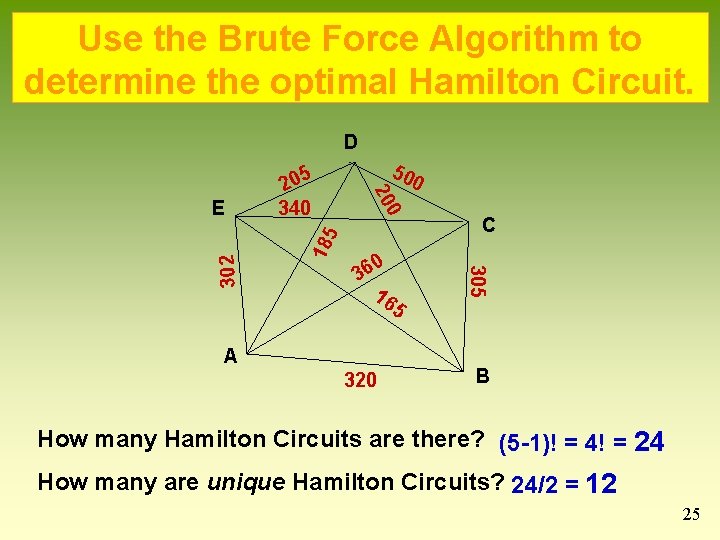
Use the Brute Force Algorithm to determine the optimal Hamilton Circuit. D 18 5 0 36 16 5 A 320 C 305 302 50 0 0 20 E 5 20 340 B How many Hamilton Circuits are there? (5 -1)! = 4! = 24 How many are unique Hamilton Circuits? 24/2 = 12 25

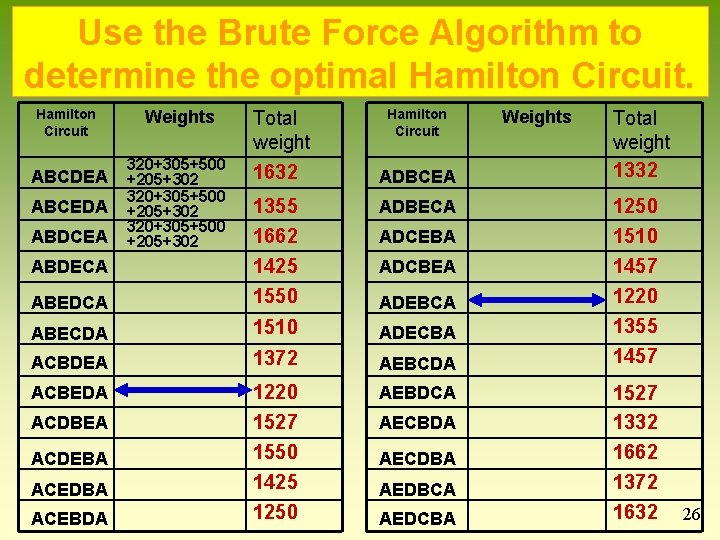
Use the Brute Force Algorithm to determine the optimal Hamilton Circuit Weights 320+305+500 +205+302 Total weight Hamilton Circuit Weights Total weight 1332 1632 ADBCEA ADBECA ABEDCA 1355 1662 1425 1550 ABECDA 1510 ADECBA ACBDEA 1372 AEBCDA ACBEDA AEBDCA ACEDBA 1220 1527 1550 1425 AEDBCA 1527 1332 1662 1372 ACEBDA 1250 AEDCBA 1632 ABCDEA ABCEDA ABDCEA ABDECA ACDBEA ACDEBA ADCBEA ADEBCA AECBDA AECDBA 1250 1510 1457 1220 1355 1457 26

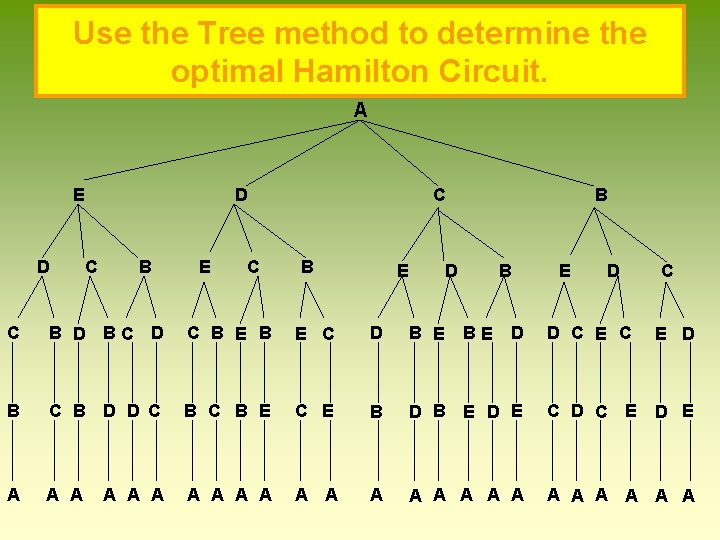
Use the Tree method to determine the optimal Hamilton Circuit. A E D D C B E C C B E B D C C B D BC D C B E C D B E D D C E D B C B D D C B E C E B D B E D E C D C E D E A A A A A A BE E

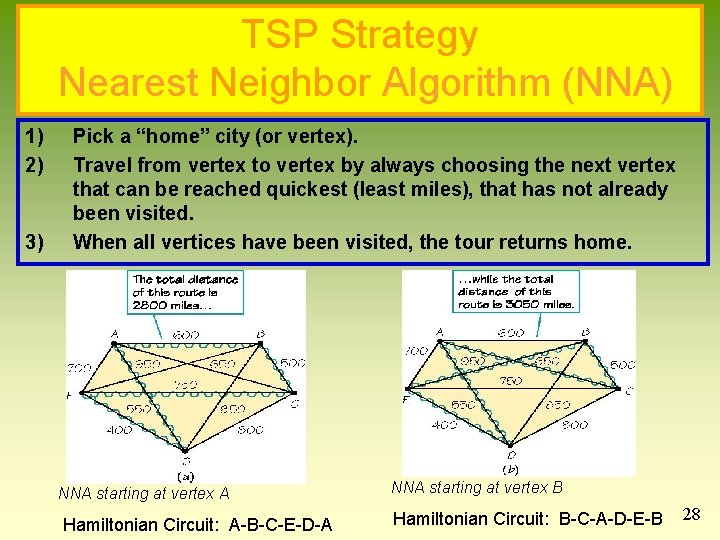
TSP Strategy Nearest Neighbor Algorithm (NNA) 1) 2) 3) Pick a “home” city (or vertex). Travel from vertex to vertex by always choosing the next vertex that can be reached quickest (least miles), that has not already been visited. When all vertices have been visited, the tour returns home. NNA starting at vertex A Hamiltonian Circuit: A-B-C-E-D-A NNA starting at vertex B Hamiltonian Circuit: B-C-A-D-E-B 28

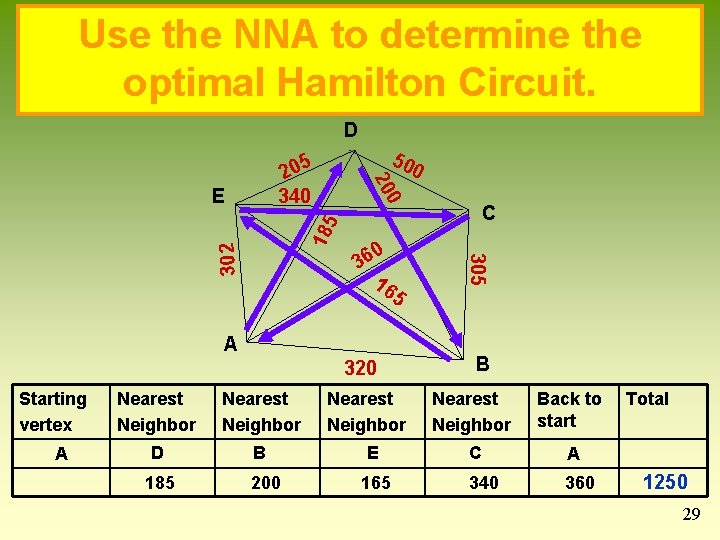
Use the NNA to determine the optimal Hamilton Circuit. D 50 0 0 36 16 5 A 320 Starting vertex A Nearest Neighbor D B 185 200 Nearest Neighbor E 165 C 305 302 18 5 E 0 20 5 20 340 B Nearest Neighbor Back to start C A 340 360 Total 1250 29

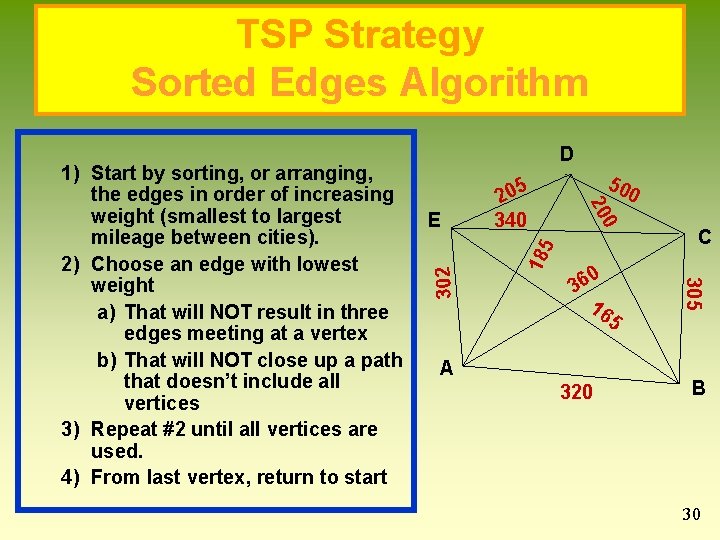
TSP Strategy Sorted Edges Algorithm 18 5 0 36 16 5 A 320 0 C 305 302 50 0 E 5 20 340 20 1) Start by sorting, or arranging, the edges in order of increasing weight (smallest to largest mileage between cities). 2) Choose an edge with lowest weight a) That will NOT result in three edges meeting at a vertex b) That will NOT close up a path that doesn’t include all vertices 3) Repeat #2 until all vertices are used. 4) From last vertex, return to start D B 30

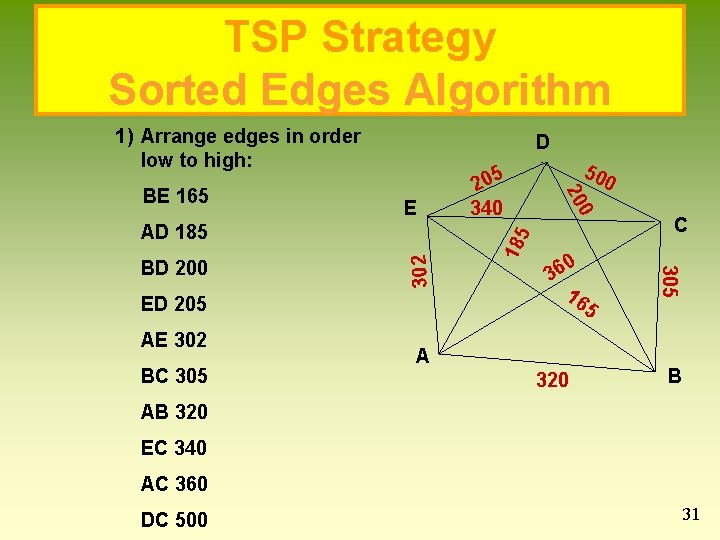
TSP Strategy Sorted Edges Algorithm 1) Arrange edges in order low to high: ED 205 AE 302 BC 305 50 0 36 16 5 A 320 0 C 305 BD 200 302 AD 185 18 5 E 5 20 340 0 20 BE 165 D B AB 320 EC 340 AC 360 DC 500 31

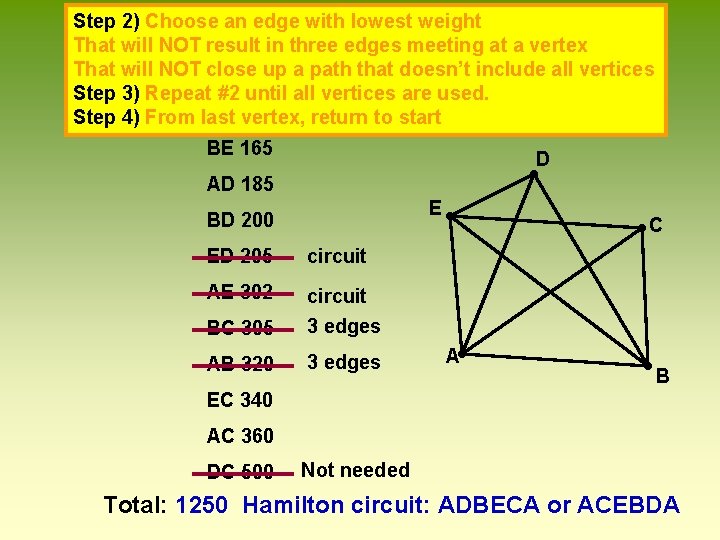
Step 2) Choose an edge with lowest weight That will NOT result in three edges meeting at a vertex That will NOT close up a path that doesn’t include all vertices Step 3) Repeat #2 until all vertices are used. Step 4) From last vertex, return to start BE 165 D AD 185 E BD 200 ED 205 circuit AE 302 BC 305 circuit 3 edges AB 320 3 edges C A B EC 340 AC 360 DC 500 Not needed Total: 1250 Hamilton circuit: ADBECA or ACEBDA

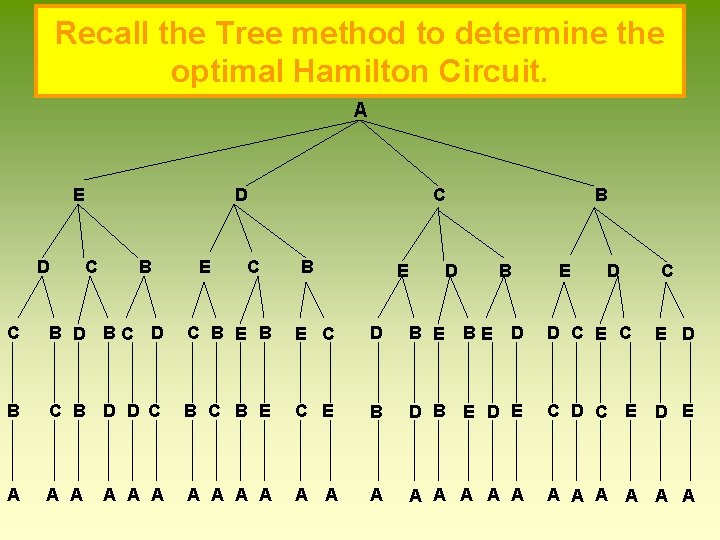
Recall the Tree method to determine the optimal Hamilton Circuit. A E D D C B E C C B E B D C C B D BC D C B E C D B E D D C E D B C B D D C B E C E B D B E D E C D C E D E A A A A A A BE E

Definition: Spanning Tree – is a subgraph that connects all vertices and has NO circuits. Therefore, you don’t go back to A at the end. Each branch of a tree is a “spanning tree”

TSP Strategy Spanning Trees A Spanning trees look more like this: E B D C C Spanning trees don’t really look like this though. E A B D 35

TSP Strategy Spanning Trees Original: E D Example 1) D E C C A A Example 2) B B D E A C B 36

Minimum-Cost Spanning Trees and Kruskal's Algorithm Goal of minimum-cost spanning tree: Create a tree that links all the vertices together and achieves the lowest cost to create. The cost of the tree is the sum of the weights on the edges. 37

Minimum-Cost Spanning Trees and Kruskal's Algorithm • Kruskal’s Algorithm — Developed by Joseph Kruskal (AT&T research). – Add links in order of cheapest cost according to the rules: • No circuit is created (no loops). –If a circuit (or loop) is created by adding the next largest link, eliminate this largest (most expensive link)—it is not needed. • Every vertex must be included in the final tree. 38

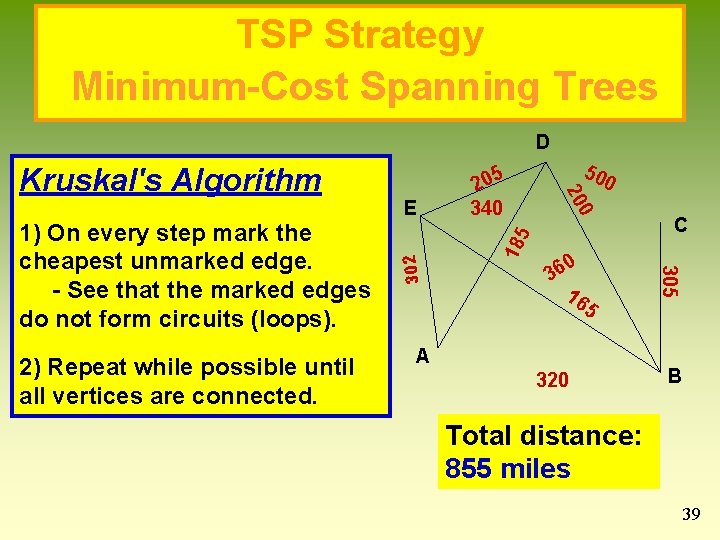
TSP Strategy Minimum-Cost Spanning Trees D 2) Repeat while possible until all vertices are connected. 18 5 302 50 0 0 36 16 5 A 320 C 305 1) On every step mark the cheapest unmarked edge. - See that the marked edges do not form circuits (loops). E 5 20 340 0 20 Kruskal's Algorithm B Total distance: 855 miles 39

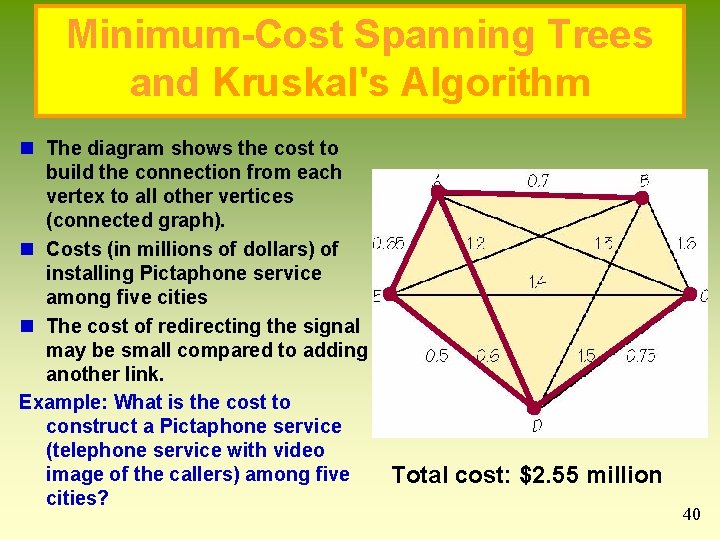
Minimum-Cost Spanning Trees and Kruskal's Algorithm n The diagram shows the cost to build the connection from each vertex to all other vertices (connected graph). n Costs (in millions of dollars) of installing Pictaphone service among five cities n The cost of redirecting the signal may be small compared to adding another link. Example: What is the cost to construct a Pictaphone service (telephone service with video image of the callers) among five cities? Total cost: $2. 55 million 40