Chapter 2 Boolean Algebra and Logic Gates Boolean

Chapter 2 Boolean Algebra and Logic Gates

Boolean Algebra (E. V. Huntington, 1904) n 1. A set of elements B and two binary operators + and ‧ Closure w. r. t. the operator + (‧) n 2. An identity element w. r. t. + (‧) n n 3. x, y Î B ' x+y ÎB 0+x = x+0 = x 1‧x = x‧ 1= x Commutative w. r. t. + (‧) n n x+y = y+x x‧y = y‧x Digital Circuits 2 -2

4. 5. 6. n ‧ is distributive over +: x‧(y+z)=(x‧y)+(x‧z) + is distributive over‧: x+(y‧z)=(x+y)‧(x+z) " x Î B, $ x' Î B (complement of x) ' x+x'=1 and x‧x'=0 $ at least two elements x, y Î B ' x ≠ y Note n n n the associative law can be derived (by truth table) no additive and multiplicative inverses Complement in 5. is not available in ordinary algebra Digital Circuits 2 -3

Two-valued Boolean Algebra n n B = {0, 1} The rules of operations Closure The identity elements (1) +: 0 (2)‧: 1 Digital Circuits 2 -4

n n The commutative laws The distributive laws Digital Circuits 2 -5

n Complement n n x+x'=1: 0+0'=0+1=1; 1+1'=1+0=1 x‧x'=0: 0‧ 0'=0‧ 1=0; 1‧ 1'=1‧ 0=0 Has two distinct elements 1 and 0, with 0 ≠ 1 Note n n a set of two elements + : OR operation; ‧ : AND operation a complement operator: NOT operation Binary logic is a two-valued Boolean algebra Digital Circuits 2 -6

Basic Theorems and Properties n Duality n n the binary operators are interchanged; AND OR the identity elements are interchanged; 1 0 Digital Circuits 2 -7

• Theorem 1(a): x+x = x – x+x = (x+x) 1 = (x+x) (x+x') = x+xx' = x+0 =x by postulate: 2(b) 5(a) 4(b) 5(b) 2(a) – Theorem 1(b): x x = x – xx = x x + 0 = xx + xx' = x (x + x') =x 1 =x Digital Circuits 2 -8

n Theorem 2 n n n x + 1 = 1 (x + 1) = (x + x')(x + 1) = x + x' 1 = x + x' =1 x 0 = 0 by duality Theorem 3: (x')' = x n n n Postulate 5 defines the complement of x, x + x' = 1 and x x' = 0 The complement of x' is x is also (x')‘=x since complement is unique Digital Circuits 2 -9
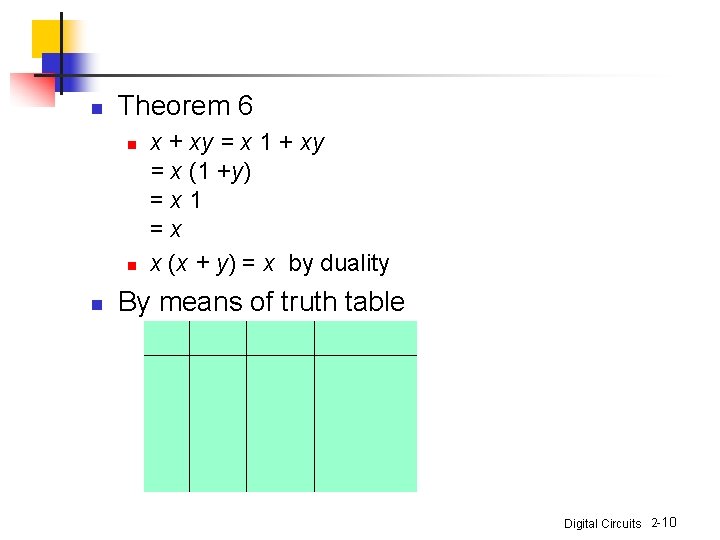
n Theorem 6 n n n x + xy = x 1 + xy = x (1 +y) =x 1 =x x (x + y) = x by duality By means of truth table Digital Circuits 2 -10

n De. Morgan's Theorems n n (x+y)' = x' y' (x y)' = x' + y' Digital Circuits 2 -11

• Operator Precedence – – – parentheses NOT AND OR examples – x y' + z – (x y + z)' Digital Circuits 2 -12

Boolean Functions n A Boolean function n n binary variables binary operators OR and AND unary operator NOT parentheses Examples n n F 1= x y z' F 2 = x + y'z F 3 = x' y' z + x' y z + x y' F 4 = x y' + x' z Digital Circuits 2 -13

n n The truth table of 2 n entries Two Boolean expressions may specify the same function n F 3 = F 4 Digital Circuits 2 -14
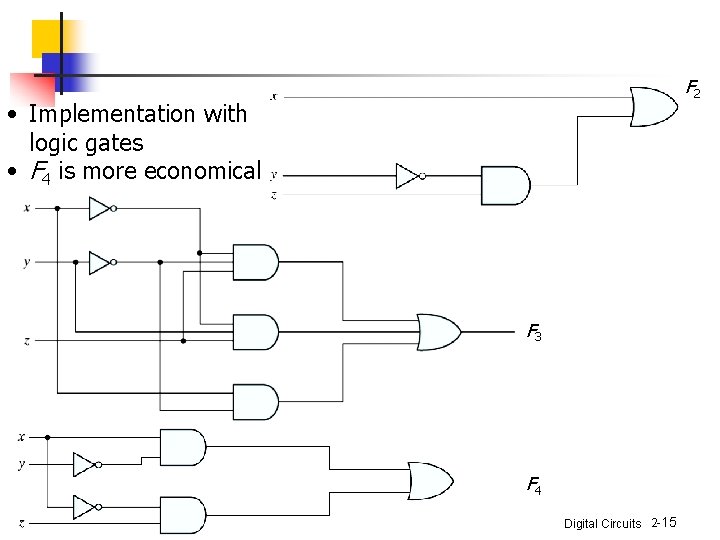
F 2 • Implementation with logic gates • F 4 is more economical F 3 F 4 Digital Circuits 2 -15

Algebraic Manipulation n To minimize Boolean expressions n n n n literal: a primed or unprimed variable (an input to a gate) term: an implementation with a gate The minimization of the number of literals and the number of terms => a circuit with less equipment It is a hard problem (no specific rules to follow) x(x'+y) = xx' + xy = 0+ xy = xy x+x'y = (x+x')(x+y) = 1 (x+y) = x+y (x+y)(x+y') = x+xy+xy'+yy' = x(1+y+y') = x Digital Circuits 2 -16

n n n x'y'z + x'yz + xy' = x'z(y'+y) + xy' = x'z + xy' xy + x'z + yz = xy + x'z + yz(x+x') = xy + x'z + yzx' = xy(1+z) + x'z(1+y) = xy +x'z (x+y)(x'+z)(y+z) = (x+y)(x'+z) by duality from the previous result Digital Circuits 2 -17

Complement of a Function n n an interchange of 0's for 1's and 1's for 0's in the value of F by De. Morgan's theorem (A+B+C)' = (A+X)' let B+C = X = A'X' by De. Morgan's = A'(B+C)' = A'(B'C') by De. Morgan's = A'B'C' associative generalizations n n (A+B+C+. . . +F)' = A'B'C'. . . F' (ABC. . . F)' = A'+ B'+C'+. . . +F' Digital Circuits 2 -18
![n n n (x'yz' + x'y'z)' = (x'yz')' (x‘y'z)' = (x+y'+z) (x+y+z') [x(y'z'+yz)]' = n n n (x'yz' + x'y'z)' = (x'yz')' (x‘y'z)' = (x+y'+z) (x+y+z') [x(y'z'+yz)]' =](http://slidetodoc.com/presentation_image/01486e0c46a8197c77fbfd0b0c52469d/image-19.jpg)
n n n (x'yz' + x'y'z)' = (x'yz')' (x‘y'z)' = (x+y'+z) (x+y+z') [x(y'z'+yz)]' = x' + ( y'z'+yz)' = x' + (y'z')' (yz)' = x' + (y+z) (y'+z') A simpler procedure n n take the dual of the function and complement each literal x'yz' + x'y'z => (x'+y+z') (x'+y'+z) (the dual) => (x+y'+z)(x+y+z') Digital Circuits 2 -19

Canonical and Standard Forms n Minterms and Maxterms n n A minterm: an AND term consists of all literals in their normal form or in their complement form For example, two binary variables x and y, n n n xy, xy', x'y' It is also called a standard product n variables can be combined to form 2 n minterms A maxterm: an OR term It is also call a standard sum 2 n maxterms Digital Circuits 2 -20
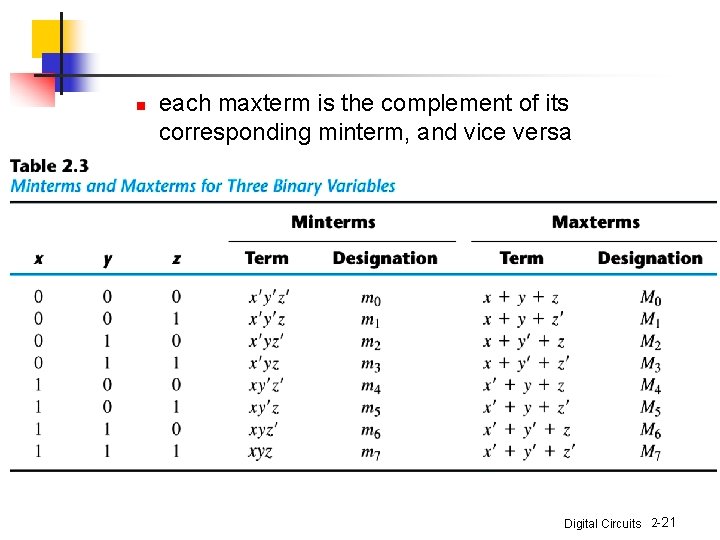
n each maxterm is the complement of its corresponding minterm, and vice versa Digital Circuits 2 -21

n An Boolean function can be expressed by n n a truth table sum of minterms f 1 = x'y'z + xy'z' + xyz = m 1 + m 4 +m 7 f 2 = x'yz+ xy'z + xyz'+xyz = m 3 + m 5 +m 6 + m 7 Digital Circuits 2 -22

n The complement of a Boolean function n n the minterms that produce a 0 f 1' = m 0 + m 2 +m 3 + m 5 + m 6 = x'y'z'+x'yz+xy'z+xyz' f 1 = (f 1')' = (x+y+z)(x+y'+z) (x+y'+z') (x'+y+z')(x'+y'+z) = M 0 M 2 M 3 M 5 M 6 Any Boolean function can be expressed as n n n a sum of minterms a product of maxterms canonical form Digital Circuits 2 -23

n Sum of minterms n n F = A+B'C = A (B+B') + B'C = AB +AB' + B'C = AB(C+C') + AB'(C+C') + (A+A')B'C =ABC+ABC'+AB'C'+A'B'C F = A'B'C +AB'C' +AB'C+ABC'+ ABC = m 1 + m 4 +m 5 + m 6 + m 7 F(A, B, C) = S(1, 4, 5, 6, 7) or, built the truth table first Digital Circuits 2 -24

n Product of maxterms n n n x + yz = (x + y)(x + z) = (x+y+zz')(x+z+yy') =(x+y+z)(x+y+z’)(x+y'+z) F = xy + x'z = (xy + x') (xy +z) = (x+x')(y+x')(x+z)(y+z) = (x'+y)(x+z)(y+z) x'+y = x' + y + zz' = (x'+y+z)(x'+y+z') F = (x+y+z)(x+y'+z)(x'+y+z') = M 0 M 2 M 4 M 5 F(x, y, z) = P(0, 2, 4, 5) Digital Circuits 2 -25

n Conversion between Canonical Forms n n n n F(A, B, C) = S(1, 4, 5, 6, 7) F'(A, B, C) = S(0, 2, 3) By De. Morgan's theorem F(A, B, C) = P(0, 2, 3) mj ' = M j sum of minterms = product of maxterms interchange the symbols S and P and list those numbers missing from the original form S of 1's P of 0's Digital Circuits 2 -26

n Example n n n F = xy + x z F(x, y, z) = S(1, 3, 6, 7) F(x, y, z) = P (0, 2, 4, 6) Digital Circuits 2 -27

n Standard Forms n n Canonical forms are seldom used sum of products = y' + zy+ x'yz' product of sums = x(y'+z)(x'+y+z'+w) F 3 = A'B'CD+ABC'D' F 1 F 2 Digital Circuits 2 -28
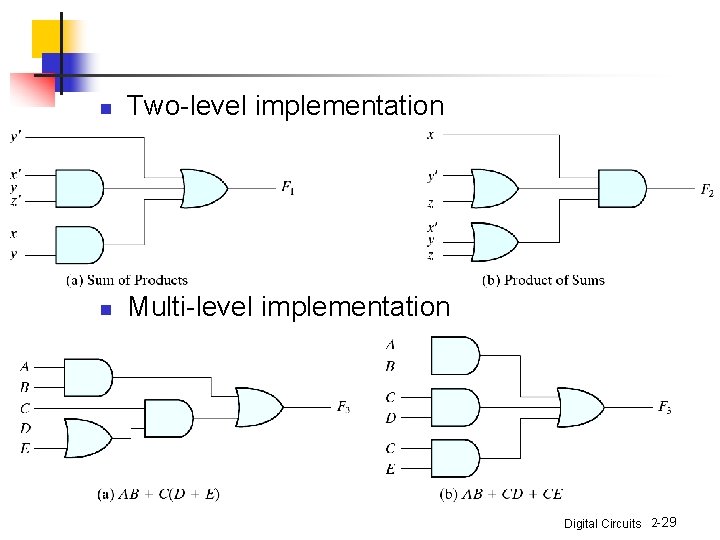
n Two-level implementation n Multi-level implementation Digital Circuits 2 -29

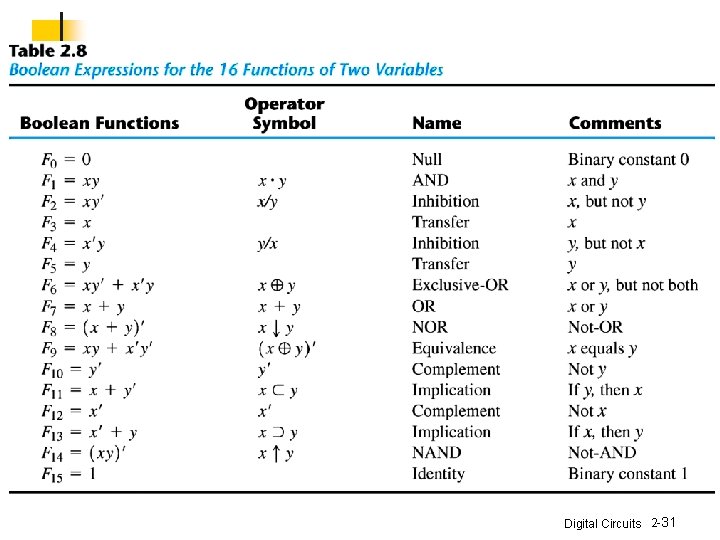
Other Logic Operations n n 2 n rows in the truth table of n binary variables n 2 2 functions for n binary variables 16 functions of two binary variables All the new symbols except for the exclusive-OR symbol are not in common use by digital designers Digital Circuits 2 -30
Digital Circuits 2 -31

Digital Logic Gates n n Boolean expression: AND, OR and NOT operations Constructing gates of other logic operations n n the feasibility and economy the possibility of extending gate's inputs the basic properties of the binary operations the ability of the gate to implement Boolean functions Digital Circuits 2 -32

n Consider the 16 functions n n n n two are equal to a constant four are repeated twice inhibition and implication are not commutative or associative the other eight: complement, transfer, AND, OR, NAND, NOR, XOR, and equivalence are used as standard gates complement: inverter transfer: buffer (increasing drive strength) equivalence: XNOR Digital Circuits 2 -33
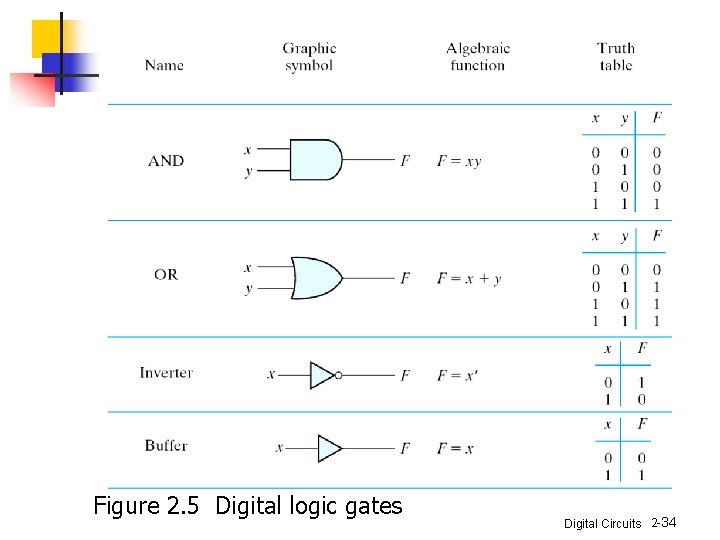
Figure 2. 5 Digital logic gates Digital Circuits 2 -34

Figure 2. 5 Digital logic gates (continued) Digital Circuits 2 -35

n Extension to multiple inputs n A gate can be extended to multiple inputs n n if its binary operation is commutative and associative AND and OR are commutative and associative n n (x+y)+z = x+(y+z) = x+y+z (x y)z = x(y z) = x y z Digital Circuits 2 -36
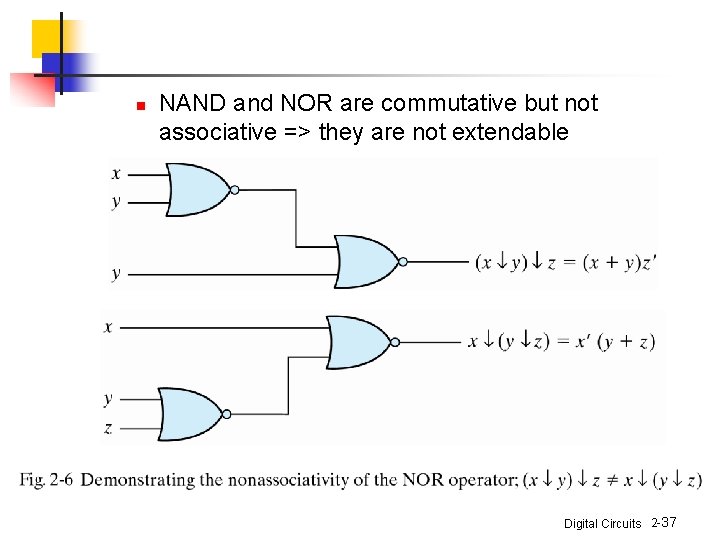
n NAND and NOR are commutative but not associative => they are not extendable Digital Circuits 2 -37
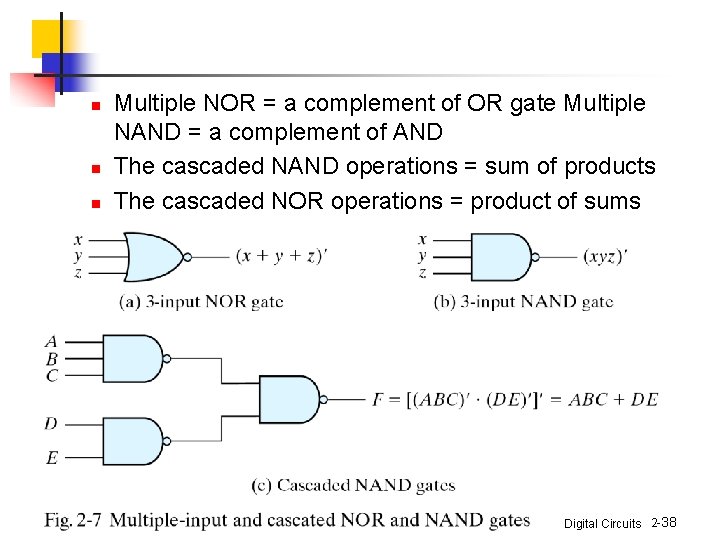
n n n Multiple NOR = a complement of OR gate Multiple NAND = a complement of AND The cascaded NAND operations = sum of products The cascaded NOR operations = product of sums Digital Circuits 2 -38
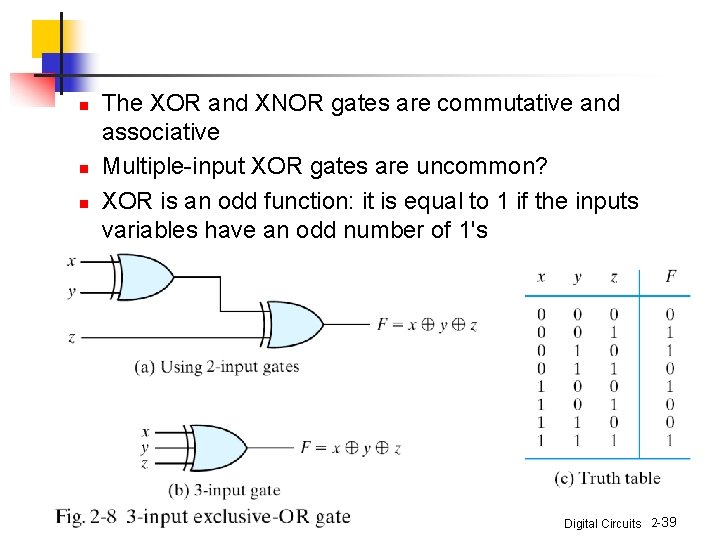
n n n The XOR and XNOR gates are commutative and associative Multiple-input XOR gates are uncommon? XOR is an odd function: it is equal to 1 if the inputs variables have an odd number of 1's Digital Circuits 2 -39

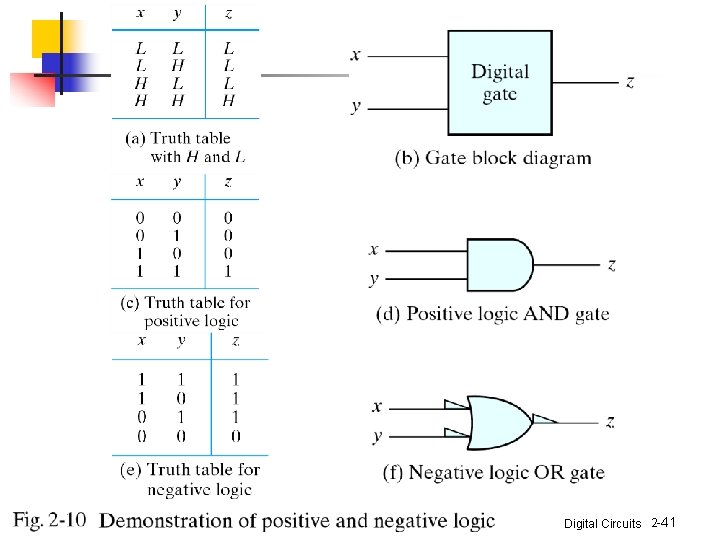
n Positive and Negative Logic n n two signal values <=> two logic values positive logic: H=1; L=0 negative logic: H=0; L=1 Consider a TTL gate n n n a positive logic NAND gate a negative logic OR gate the positive logic is used in this book Digital Circuits 2 -40
Digital Circuits 2 -41

Integrated Circuits n n n An IC (a chip) Examples: SSI: < 10 gates MSI: 10 ~ 100 gates LSI: 100 ~ xk gates VLSI: > xk gates n n n small size (compact size) low cost low power consumption high reliability high speed Digital Circuits 2 -42

n Digital logic families: circuit technology n n n TTL: transistor-transistor logic (dying? ) ECL: emitter-coupled logic (high speed, high power consumption) MOS: metal-oxide semiconductor (NMOS, high density) CMOS: complementary MOS (low power) Bi. CMOS: high speed, high density Digital Circuits 2 -43

n The characteristics of digital logic families n n Fan-out: the number of standard loads that the ouput of a typical gate can drive Power dissipation Propagation delay: the average transition delay time for the signal to propagate from input to output Noise margin: the minimum of external noise voltage that caused an undesirable change in the circuit output Digital Circuits 2 -44

n CAD – Computer-Aided Design n n Millions of transistors Computer-based representation and aid Automatic the design process Design entry n n Schematic capture HDL – Hardware Description Language n n n Verilog, VHDL Simulation Physical realization n ASIC, FPGA, PLD Digital Circuits 2 -45

Digital Circuits 2 -46
- Slides: 46