CHAPTER 2 ATOMIC STRUCTURE 2 1 Bohrs Atomic

CHAPTER 2 ATOMIC STRUCTURE

2. 1 Bohr’s Atomic Model

Learning Outcomes At the end of this topic students should be able to: - a) Describe the Bohr’s atomic model. b) Explain the existence of electron energy levels in an atom. c) Calculate the energy of electron at its level (orbit) using.

Learning Outcomes d) Describe the formation of line spectrum of hydrogen atom. e) Calculate the energy change of an electron during transition. f) Calculate the photon of energy emitted by an electron that produces a particular wavelength during transition.

Learning Outcomes g) Perform calculation involving the Rydberg equation for Lyman, Balmer, Paschen, Brackett and Pfund series: g) Calculate the ionisation energy of hydrogen atom from the Lyman series.

Learning Outcomes i) State the weaknesses of Bohr’s atomic model. j) State the dual nature of electron using de Broglie’s postulate and Heisenberg’s uncertainty principle.

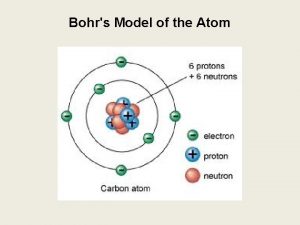
Bohr’s Atomic Model In 1913, a young Dutch physicist, Niels Böhr proposed a theory of atom that shook the scientific world. The atomic model he described had electrons circling a central nucleus that contains positively change proton.
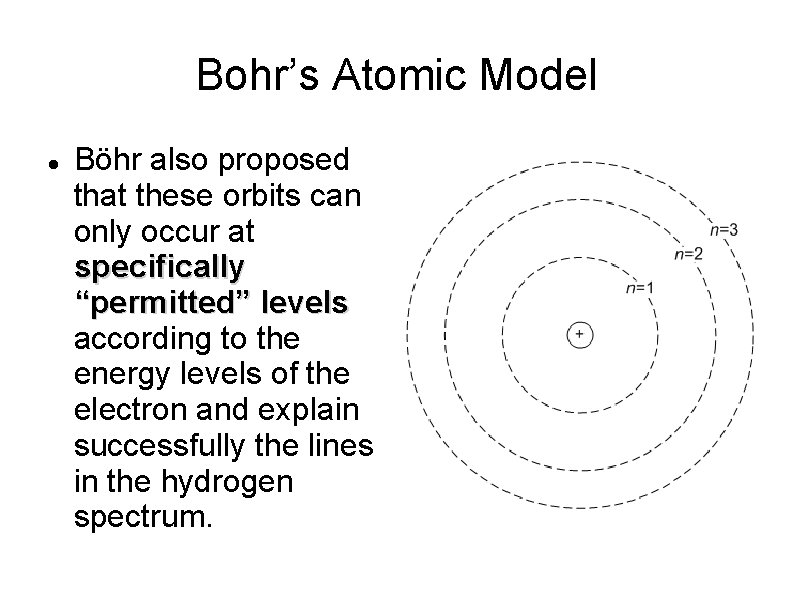
Bohr’s Atomic Model Böhr also proposed that these orbits can only occur at specifically “permitted” levels according to the energy levels of the electron and explain successfully the lines in the hydrogen spectrum.
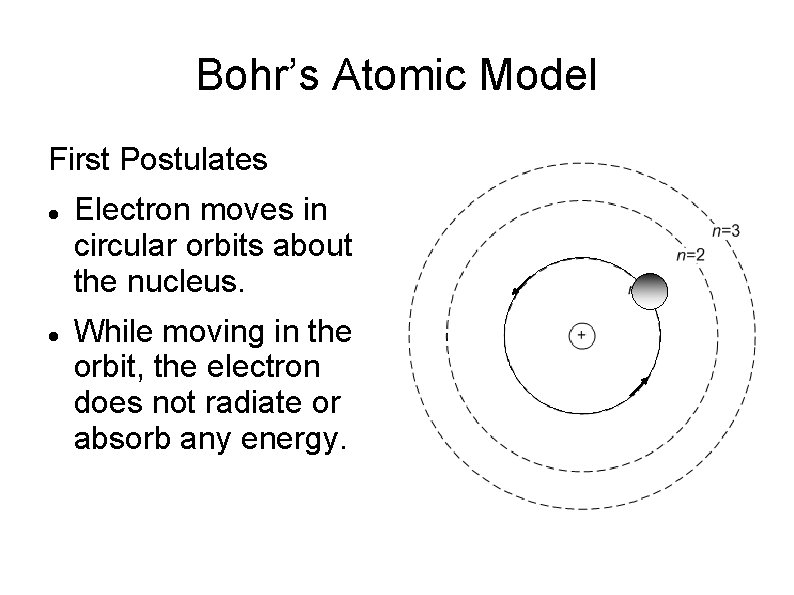
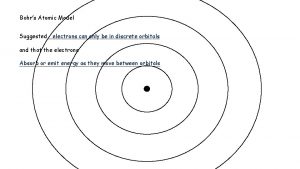
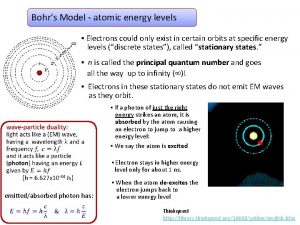
Bohr’s Atomic Model First Postulates Electron moves in circular orbits about the nucleus. While moving in the orbit, the electron does not radiate or absorb any energy.
![[orbit = energy level=shell] Orbit is a pathway where the electron is move [orbit = energy level=shell] Orbit is a pathway where the electron is move](http://slidetodoc.com/presentation_image_h/23c158df63f091c38282ebf8e03b6b37/image-10.jpg)
[orbit = energy level=shell] Orbit is a pathway where the electron is move around the nucleus. Orbit
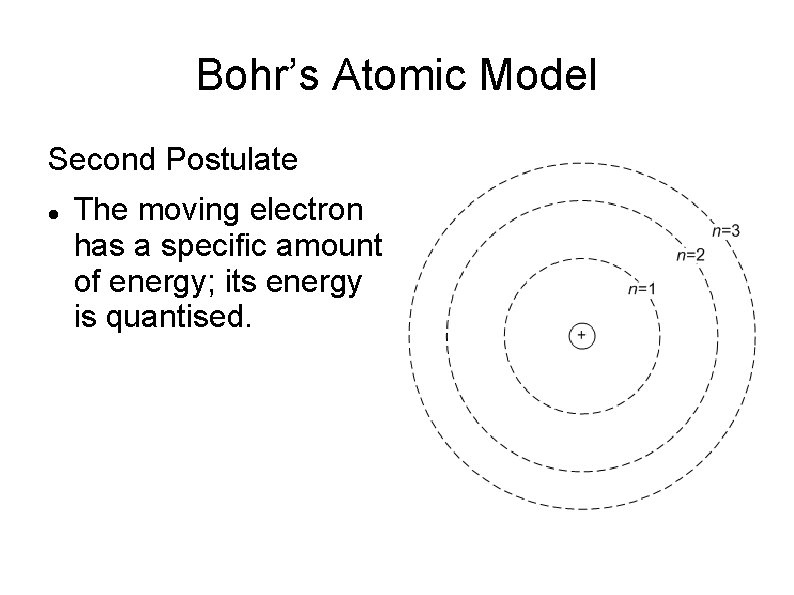
Bohr’s Atomic Model Second Postulate The moving electron has a specific amount of energy; its energy is quantised.

The energy of an electron in its level is given by: RH (Rydberg constant) = 2. 18 x 10 -18 J. n (principal quantum number) = 1, 2, 3 …. ∞ (integer) Note: n identifies the orbit of electron Energy is zero if electron is located infinitely far from nucleus

Bohr’s Atomic Model Third postulate At ordinary conditions, the electron is at the ground state (lowest level). If energy is supplied, electron absorbed the energy and is promoted from a lower energy level to a higher ones. (Electron is excited)

Bohr’s Atomic Model Fourth Postulate Electron at its excited states is unstable. It will fall back to lower energy level and released a specific amount of energy in the form of light (photon). The energy of the photon equals the energy difference between levels.
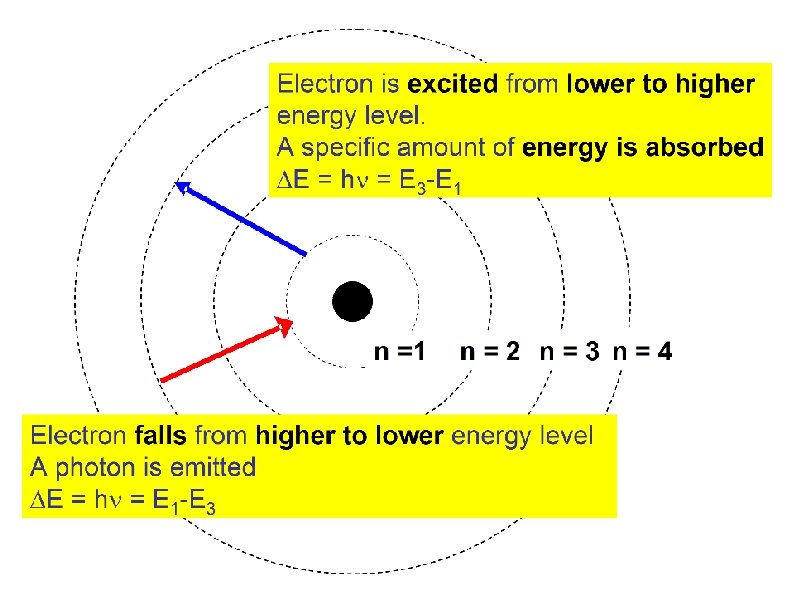
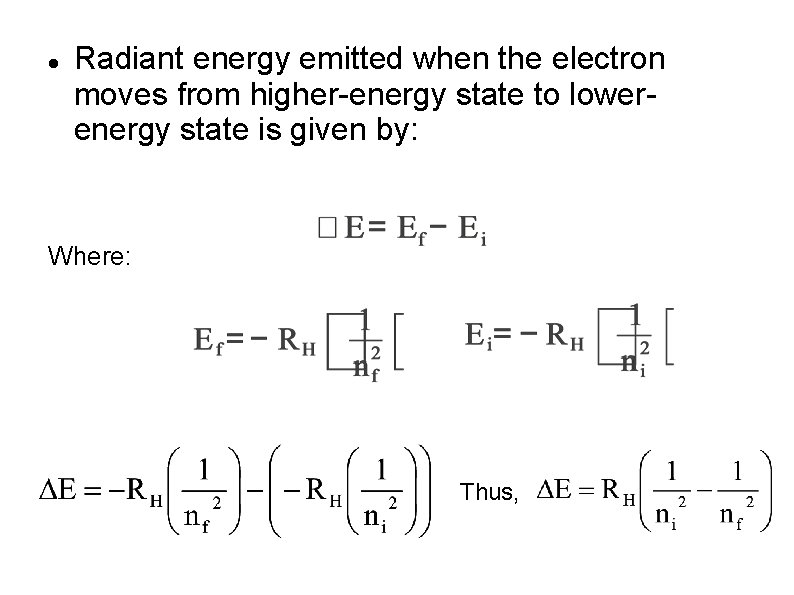
Radiant energy emitted when the electron moves from higher-energy state to lowerenergy state is given by: Where: Thus,
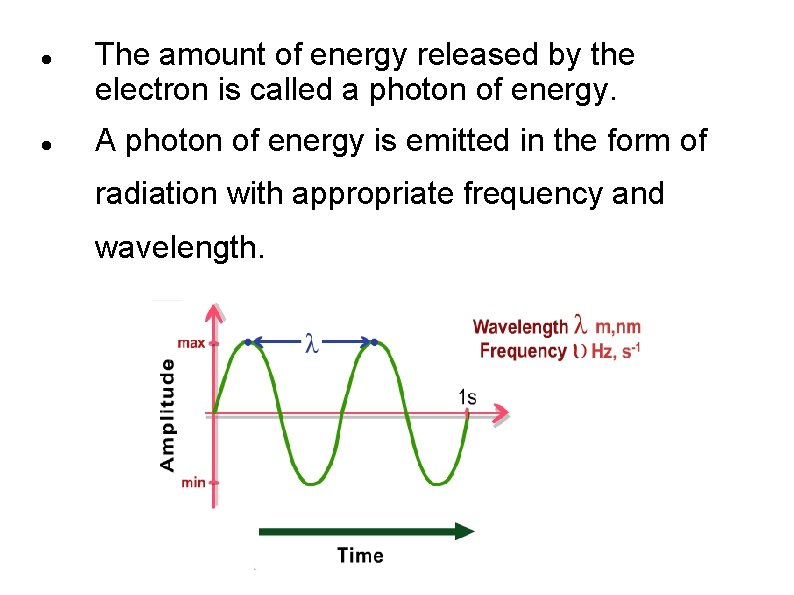
The amount of energy released by the electron is called a photon of energy. A photon of energy is emitted in the form of radiation with appropriate frequency and wavelength.

Where : h (Planck's constant) = 6. 63 x 10 -34 J s v = frequency (s-1) Where : c (speed of light) = 3. 00 x 108 ms-1 Thus :

Rydberg Equation Wavelength emitted by the transition of electron between two energy levels is calculated using Rydberg equation:

Example 1 Calculate the wavelength, in nanometers of the spectrum of hydrogen corresponding to n = 2 and n = 4 in the Rydberg equation.

Exercises: 1. Calculate the energy of hydrogen electron in the: (a) 1 st orbit (b) 3 rd orbit (c) 8 th orbit 1. Calculate the energy change (J), that occurs when an electron falls from n = 5 to n = 3 energy level in a hydrogen atom. 2. Calculate the frequency and wavelength (nm) of the radiation emitted in question 2.
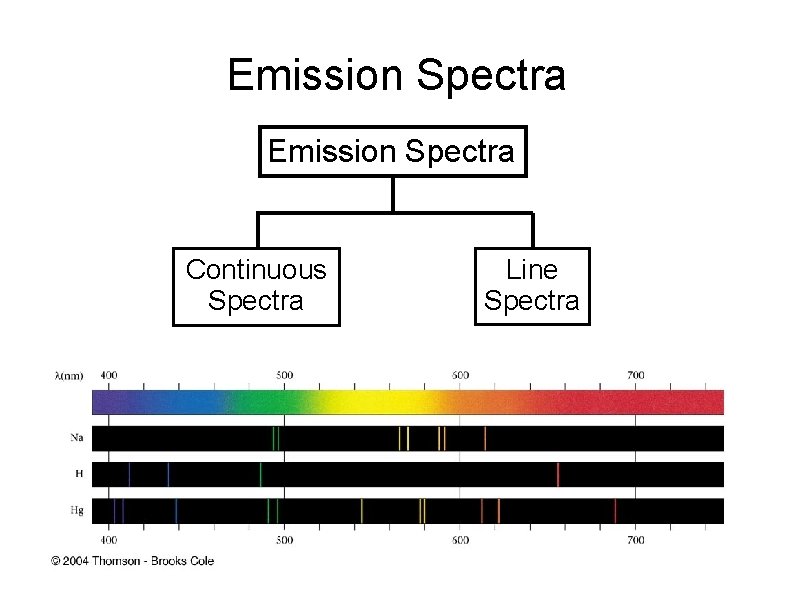
Emission Spectra Continuous Spectra Line Spectra

Continuous Spectrum A spectrum consists of radiation distributed over all wavelength without any blank spot. Example : electromagnetic spectrum, rainbow It is produced by white light (sunlight or incandescent lamp) that passed through a prism
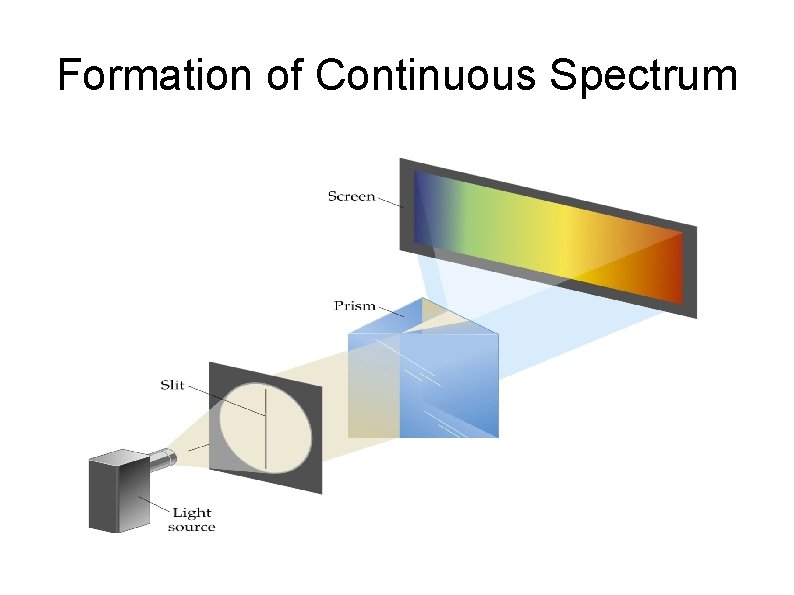
Formation of Continuous Spectrum
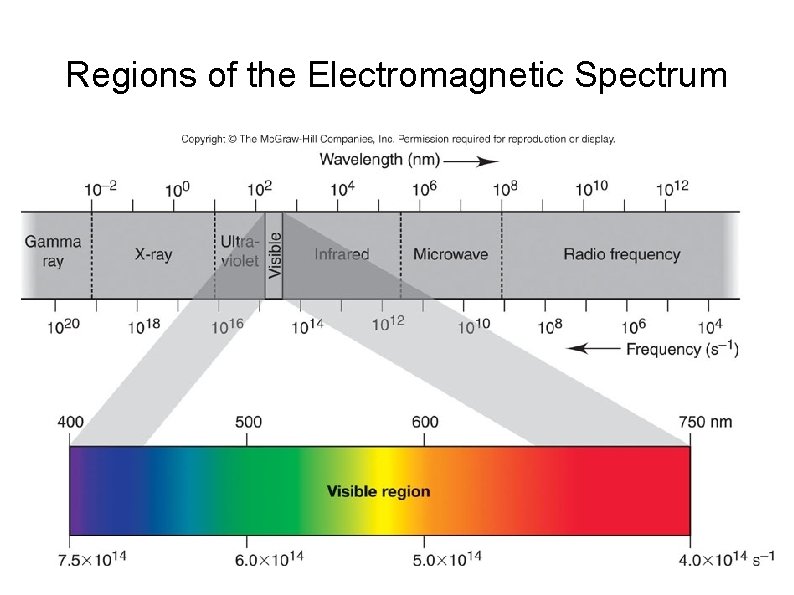
Regions of the Electromagnetic Spectrum

Line Spectrum (atomic spectrum) A spectrum consists of discontinuous & discrete lines with specific wavelength. It is composed when the light from a gas discharge tube containing a particular element is passed through a prism.

Formation of Atomic / Line Spectrum The emitted light (photons) is then separated into its components by a prism. Each component is focused at a definite position, according to its wavelength and forms as an image on the photographic plate. The images are called spectral lines.
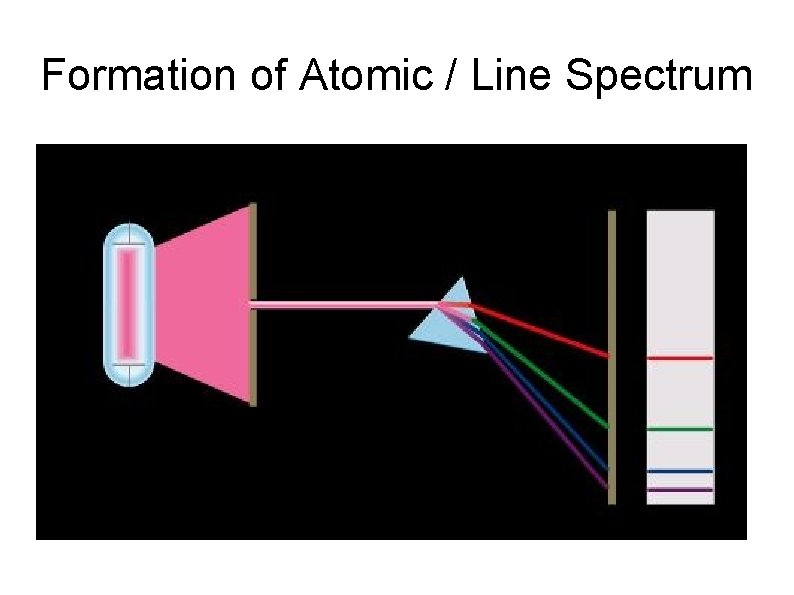
Formation of Atomic / Line Spectrum

Formation of Atomic / Line Spectrum Example : The line emission spectrum of hydrogen atom Line spectrum are composed a few wavelengths giving a series of discrete line separated by blank areas It means each line corresponds to a specific wavelength or frequency.

Formation of Line Spectrum When electron absorbed radiant energy, they will move from lower energy level to higher energy level (excited state). This excited electron is unstable and it will fall back to lower energy level. During the transition, electron will release energy in the form of light with specific wavelength and can detected as a line spectrum.

Differences Between Line & Continuous Spectra Continuous Spectrum A spectrum that contains all wavelength without any blank spots. Line Spectrum Example: Rainbow. A spectrum that contain only specific wavelengths. A spectrum of discrete lines with certain wavelengths. Example: Emission spectrum an element.
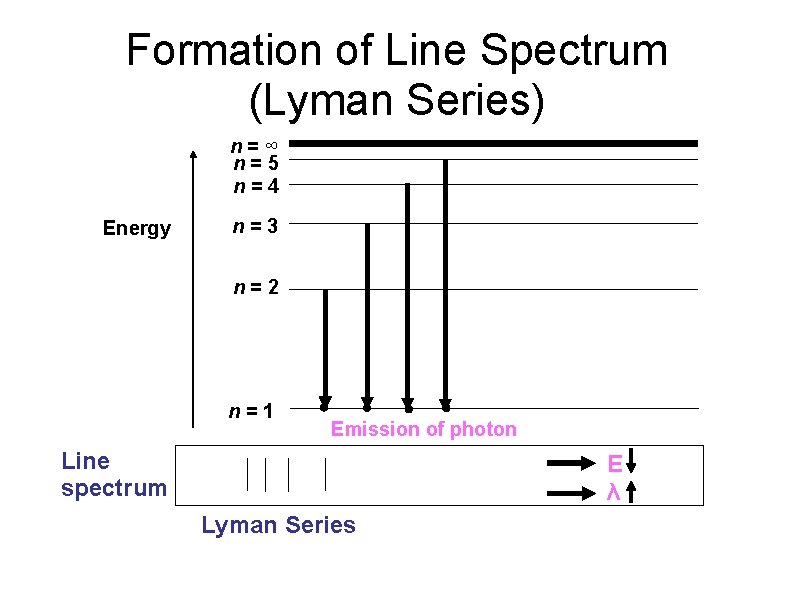
Formation of Line Spectrum (Lyman Series) n=∞ n=5 n=4 Energy n=3 n=2 n=1 Emission of photon Line spectrum E λ Lyman Series
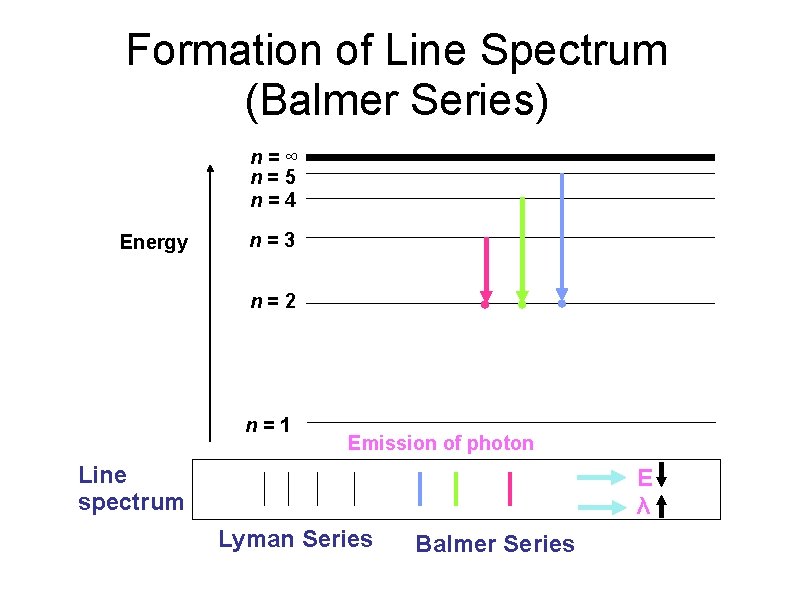
Formation of Line Spectrum (Balmer Series) n=∞ n=5 n=4 Energy n=3 n=2 n=1 Emission of photon Line spectrum E λ Lyman Series Balmer Series
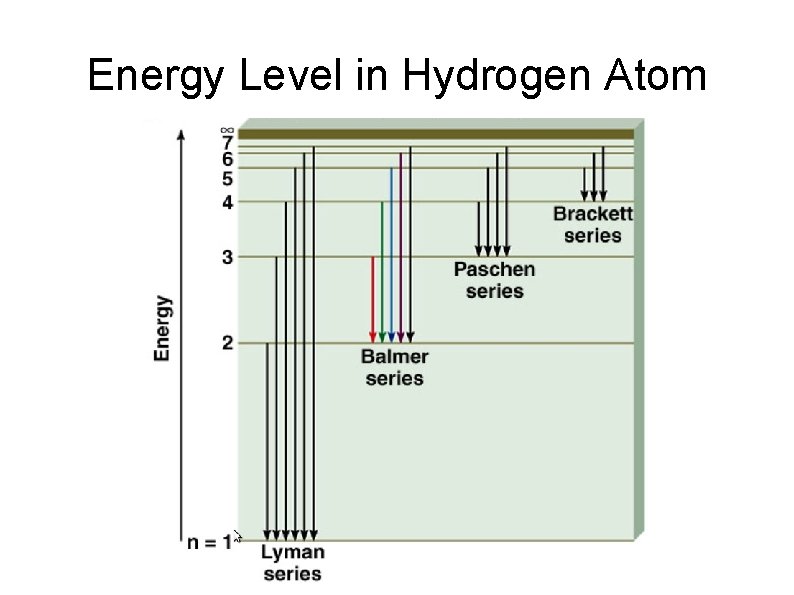
Energy Level in Hydrogen Atom
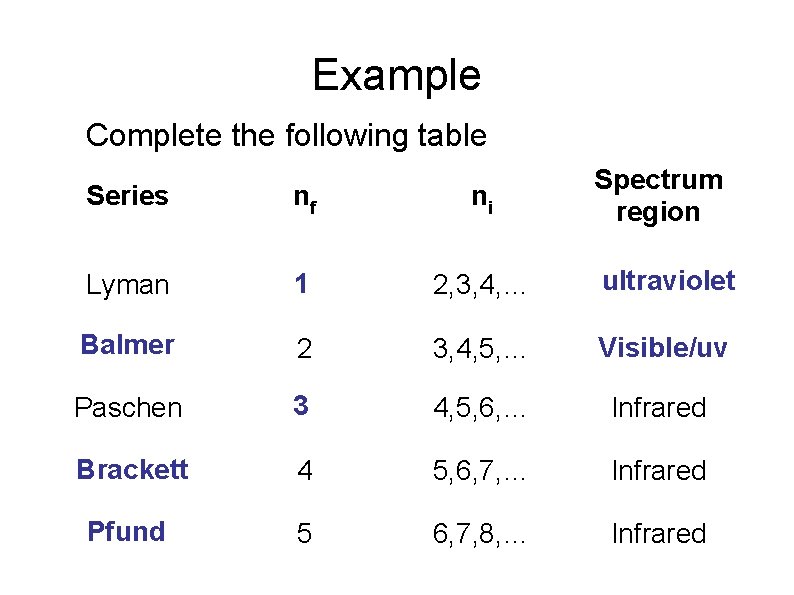
Example Complete the following table Spectrum region Series nf ni Lyman 1 2, 3, 4, … ultraviolet Balmer 2 3, 4, 5, … Visible/uv Paschen 3 4, 5, 6, … Infrared Brackett 4 5, 6, 7, … Infrared Pfund 5 6, 7, 8, … Infrared
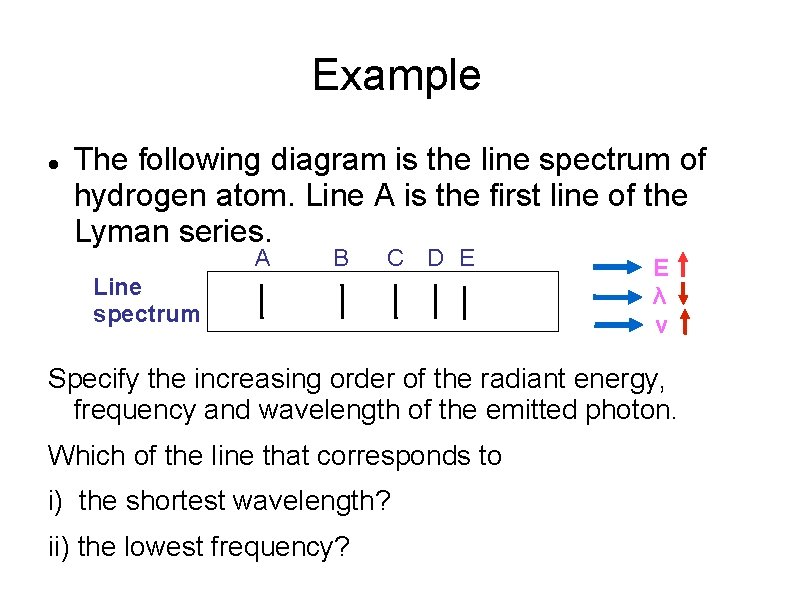
Example The following diagram is the line spectrum of hydrogen atom. Line A is the first line of the Lyman series. A B C D E Line spectrum E λ v Specify the increasing order of the radiant energy, frequency and wavelength of the emitted photon. Which of the line that corresponds to i) the shortest wavelength? ii) the lowest frequency?
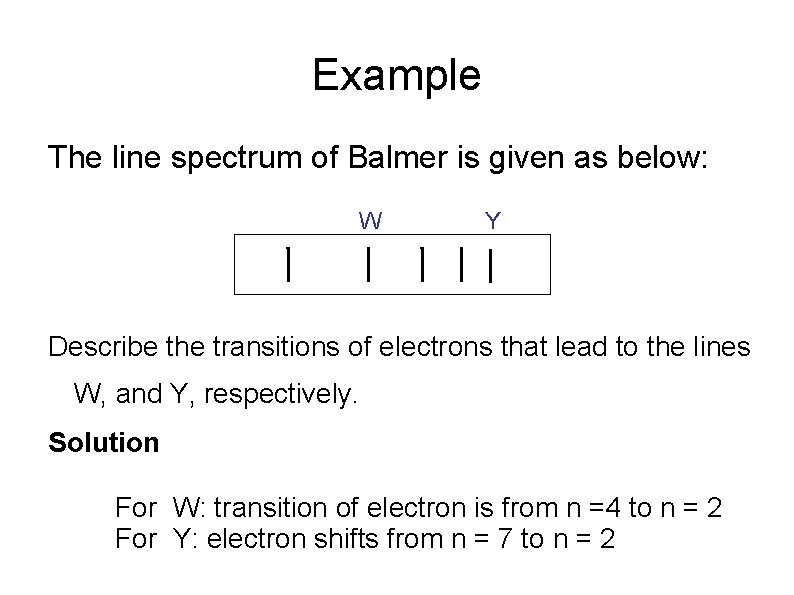
Example The line spectrum of Balmer is given as below: W Y Describe the transitions of electrons that lead to the lines W, and Y, respectively. Solution For W: transition of electron is from n =4 to n = 2 For Y: electron shifts from n = 7 to n = 2

Example E Line spectrum (a) D C B A Paschen series Which of the line in the Paschen series corresponds to the longest wavelength of photon? (b) Describe the transition that gives rise to the line. Solution Line A. The electron moves from n=4 to n=3.

Example With refer to the second line in the Balmer series of the hydrogen spectrum, Calculate; a)the wavelength in nm b)the frequency c) the energy

Example Refer to last line of hydrogen spectrum in Lyman series, Calculate: a) Wavelength b) Frequency c) Wave number; where wave number = For Lyman series; n 1 = 1 & n 2 = ∞ Ans: i. 9. 116 x 10 -8 m ii. 3. 29 x 1015 s-1 iii. 1. 0970 X 107 m-1

Ionization Energy Defination : Ionization energy is the minimum energy required to remove an electron in its ground state from an atom (or an ion) in gaseous state. M (g) → M+ (g) + e ∆H = +ve

Ionization Energy The hydrogen atom is ionised when electron is removed from its ground state (n = 1) to n = ∞. At n = ∞, the potential energy of electron is zero, here the nucleus attractive force has no effect on the electron (electron is free from nucleus)

Example n 1 = 1, n 2 = ∞ ∆E = = RH (1/n 12 – 1/n 22) = 2. 18 x 10 -18 (1/12 – 1/∞ 2) = 2. 18 x 10 -18 (1 – 0) 2. 18 x 10 -18 J Ionisation energy = = 2. 18 x 10 -18 x 6. 02 x 1023 J mol-1 1. 312 x 106 J mol-1 = 1312 k. J mol-1

Example Calculate the energy to ionized : (a) a hydrogen atom. (b) 1 mol of hydrogen atom.
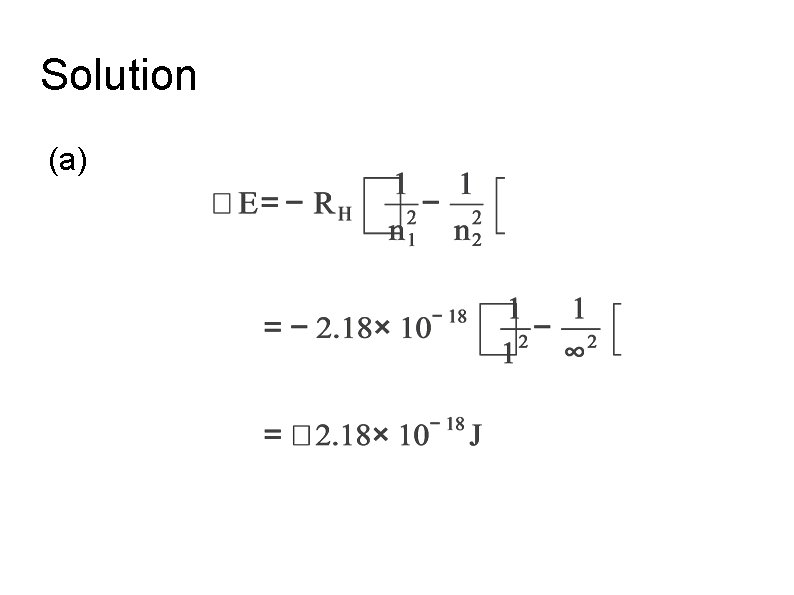
Solution (a)

Solution (b) 1 H atoms need 2. 18 x 1018 J 1 mol H atom = 2. 18 x 1018 x 6. 02 x 1023 = 1. 31 x 106 J The energy to ionized 1 mol of hydrogen atom is 1. 31 X 106 J

Example 10. 97 10. 66 10. 52 10. 27 9. 74 8. 22 The Lyman series of the spectrum of hydrogen is shown above. Calculate the ionisation energy of hydrogen from the spectrum.

Solution ΔE = h X c/λ = h x c x wave no. = (6. 626 x 10 -34 Js)(3 x 108 ms-1)(10. 97 x 106 m-1) = 218. 06 x 10 -20 J = 2. 18 x 10 -18 J Ionisation energy = (2. 18 x 10 -18) (6. 02 x 1023 J mol-1) = 1. 312 x 106 J mol-1 = 1312 k. J mol-1

The weaknesses of Bohr’s Theory It can only explain the hydrogen spectrum or any spectrum of ions contain one electron. example: He+, Li 2+. Therefore, it did not account for the emission spectrum of atom containing more than 1 electron. Electron are wavelike, we can’t define the precise location of a wave because a wave extends in space.

de Broglie’s Postulate In 1924 Louis de Broglie proposed that not only light but all matter has a dual nature and possesses both wave and particle properties. Electron is both particle and wave. Tiny particle such as electron does have wave properties. De Broglie deduced that the particle and wave properties are related by the expression:

Example Electron has dual nature properties. Why don't we see the wave properties of a Baseball?

de Broglie’s Postulate h = Planck constant (J s) m = particle mass (kg) μ = velocity (m/s) λ = wavelength of a matter wave

Heisenberg’s Uncertainty Principle It is impossible to know simultaneously both the momentum p (defined as mass times velocity) and the position of a particle with certain. Stated mathematically, where Δx = uncertainty in measuring the position Δp = uncertainty in measuring the momentum = Δmv h = Planck constant

2. 2 Quantum Mechanical Model

Learning Outcomes At the end of this topic students should be able to: Define the term orbital. State the four quantum numbers in an orbitals. sketch the 3 -D shape of s, p and d orbitals.
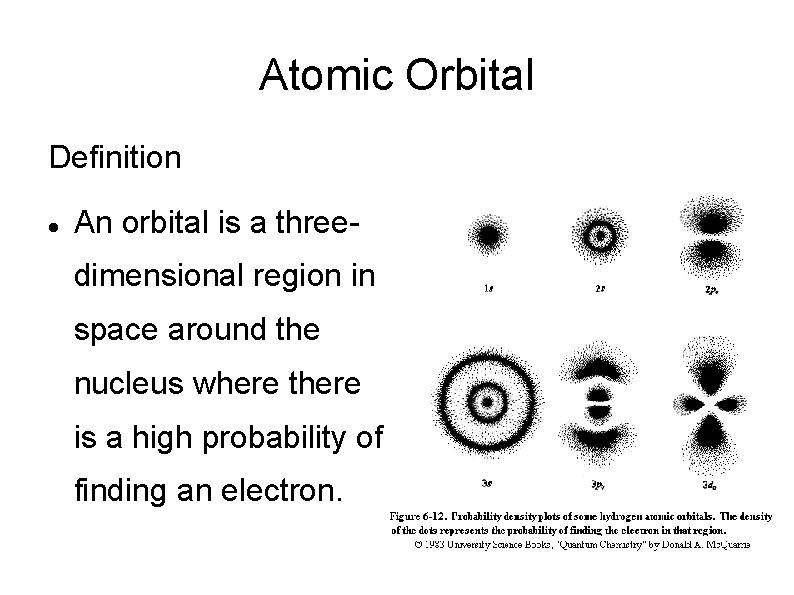
Atomic Orbital Definition An orbital is a threedimensional region in space around the nucleus where there is a high probability of finding an electron.

Quantum Numbers Each of the electrons in an atom is described and characterised by a set of four quantum numbers, namely principal quantum number, n angular momentum quantum number, l magnetic quantum number, m electron spin quantum number, s.

Principal Quantum Number, n n determines the energy level (electron shell) and size of an orbital. The principal quantum number n, may have +ve value starting from n =1, 2, 3, …, ∞. As n increase : i) the orbital become larger ii) electron has higher energy
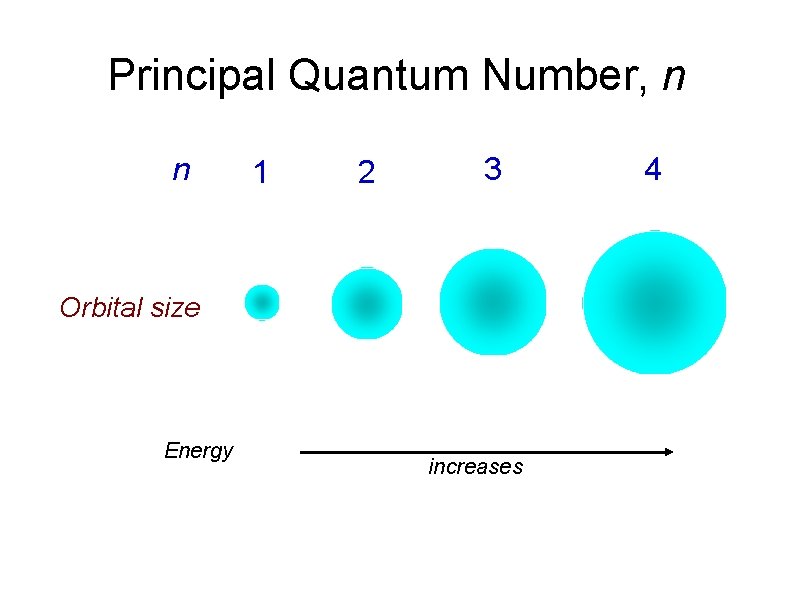
Principal Quantum Number, n n 1 2 3 Orbital size Energy increases 4

Angular Momentum Quantum Number, l Alternative name: - Subsidiary Quantum Number - Azimuthal Quantum Number - Orbital Quantum Number The value of l indicates the shape of the atomic orbital. The allowed values of l are 0, 1, 2, …, ( n - 1)

Angular Momentum Quantum Number, l Letters are assigned to different numerical values of Value of l 0 1 2 3 Symbol Orbital shape s spherical p dumbbell d cloverleaf f

Angular Momentum Quantum Number, l value is depend on n. (i. e. , 0 ≤ l < n). One subshell If n = 1, l = 0 (s-orbital) (s orbital) If n = 2, l = 0 (s-orbital) two subshells (s and p orbitals) = 1 (p-orbital) If n = 3, l = 0 (s-orbital) = 1 (p-orbital) = 2 (d-orbital) three subshells (s, p, and dorbitals)

Magnetic Quantum Number, m Describe the orientation of orbitals in space. Possible values of m depend on the value of l. For a given l, m can be : -l, …, 0, …, +l Example: If l = 0, m = 0 » 1 orientation of s orbital If l = 1, m = -1, 0, +1 » 3 orientation of p orbital (px, py, pz) If l = 2, m = -2, -1, 0, +1, +2 » 5 orientation of d orbital ( dxy, dxz, dyz, dx 2 -y 2, dz 2)

Electron Spin Quantum Number, s The value of s represent the direction of an electron rotation on its own axis. either clockwise or anticlockwise It has 2 value : +½ and -½

Shape of Atomic Orbital s orbitals Spherical shape with the nucleus at the centre. When l = 0 , m = 0 , only 1 orientation of s orbital. The larger value of n, the size of s orbital gets larger.
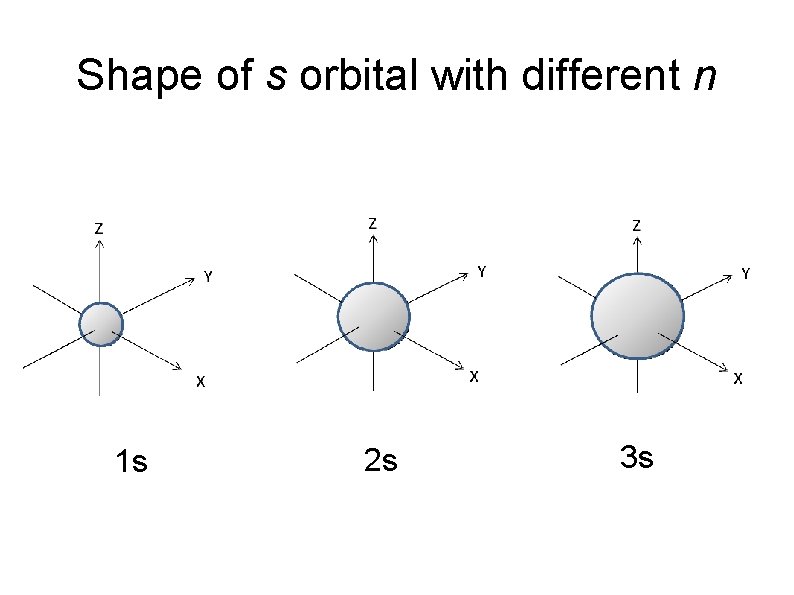
Shape of s orbital with different n 1 s 2 s 3 s

Shape of Atomic Orbitals p orbitals Can be represent as a pair of dumb-bell shaped When l = 1, m = -1, 0, +1 3 orientation of p-orbitals px, py, and pz. As n increases, the p orbitals get larger.
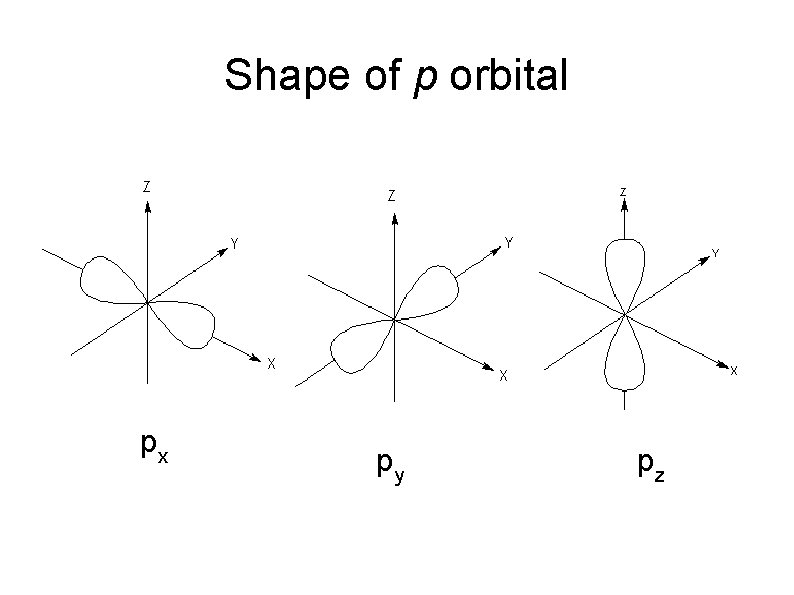
Shape of p orbital px py pz

Shape of Atomic Orbitals d orbitals All the d orbitals do not look alike. When l = 2 , m = -2, -1, 0, +1, +2. There are five orientation of d orbitals.
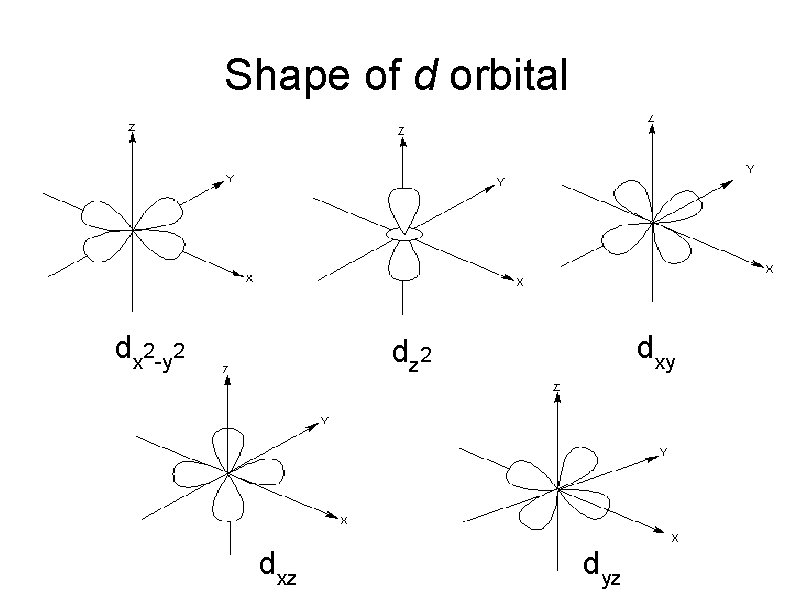
Shape of d orbital dx 2 -y 2 dxy dz 2 dxz dyz

Set of Four Quantum Numbers 4 quantum number n, l, m and s enable us to label completely an electron in any orbital of an atom. Example: 4 quantum numbers of 2 s orbital electron are n = 2 , l = 0 , m = 0 and s = +½ and -½ Can be simplified as (2, 0, 0, +½) or (2, 0, 0, -½) n, l , m, s

Exercise Shell n 1 2 l Orbital notation m No. of orbitals 0 1 0 2 s 0 1 1 2 p -1, 0, +1 3

Exercise Predict the following quantum numbers whether they are allowed or not (a) (1, 0, 0, -½) (b) (2, 0, 1, 1) (c) (0, 1, 1, +½) (d) (4, 1, 0, -½)

2. 3 Electronic Configuration

Learning Outcomes At the end of this topic students should be able to: State and apply Aufbau principle, Hund's rule and Pauli exclusion principle in filling of electrons in orbitals of an atom. Write the electronic configuration of atoms and monoatomic ions. (a) Orbital diagram (b) spdf notation

Learning Outcomes Explain the anomalous electronic configurations of chromium and copper.

Introduction The electronic configuration of an atom show electron are filled in the orbital. Electronic configuration describes the arrangement of electron in an atom.
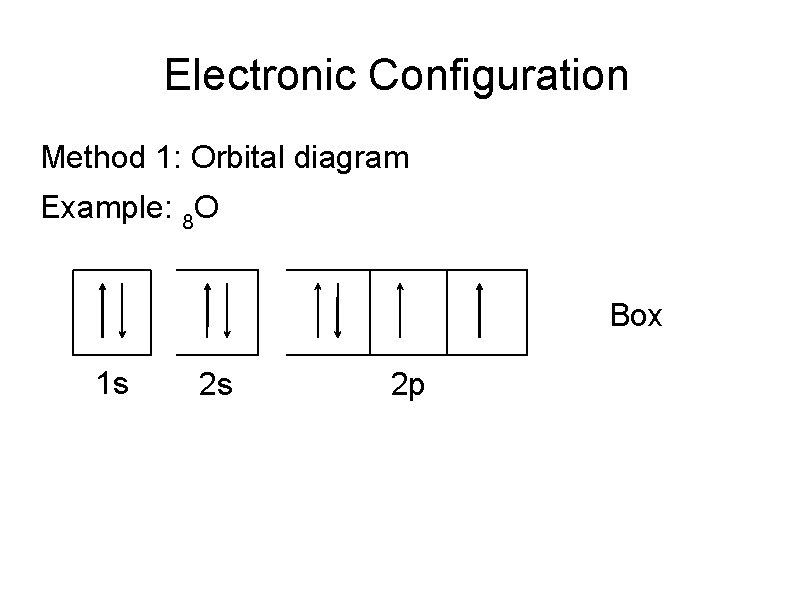
Electronic Configuration Method 1: Orbital diagram Example: 8 O Box 1 s 2 s 2 p
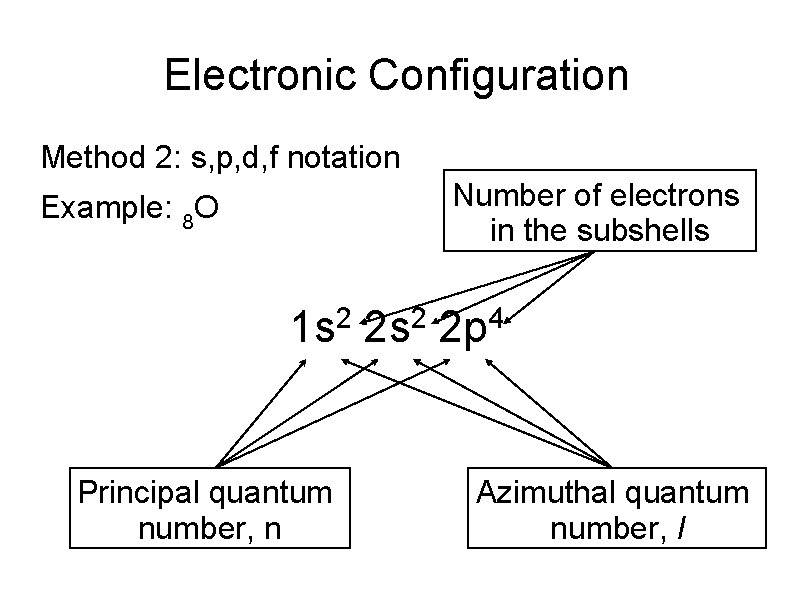
Electronic Configuration Method 2: s, p, d, f notation Number of electrons in the subshells Example: 8 O 2 2 1 s 2 s 2 p Principal quantum number, n 4 Azimuthal quantum number, l

Electronic Configuration To enable us to do electronic configuration, we have to obey the following rules: a) The Aufbau Principle b) The Pauli Exclusion Principle c) The Hund rule

Aufbau Principle State that electrons are filled in the orbitals in order of increasing energy. Electrons should occupy the orbital with the lowest energy first before enters the one with higher energy.
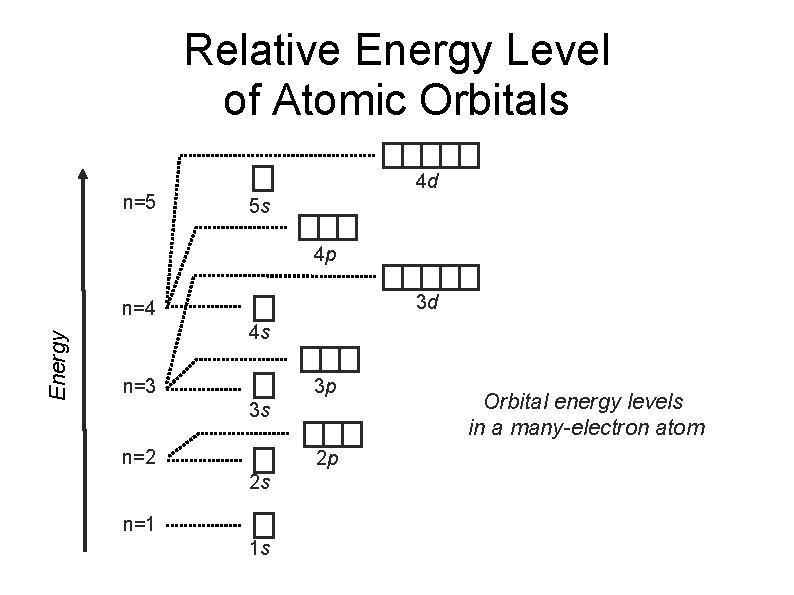
Relative Energy Level of Atomic Orbitals n=5 4 d 5 s 4 p 3 d e n e rg y Energy n=4 4 s n=3 3 p 3 s n=2 2 p 2 s n=1 1 s Orbital energy levels in a many-electron atom
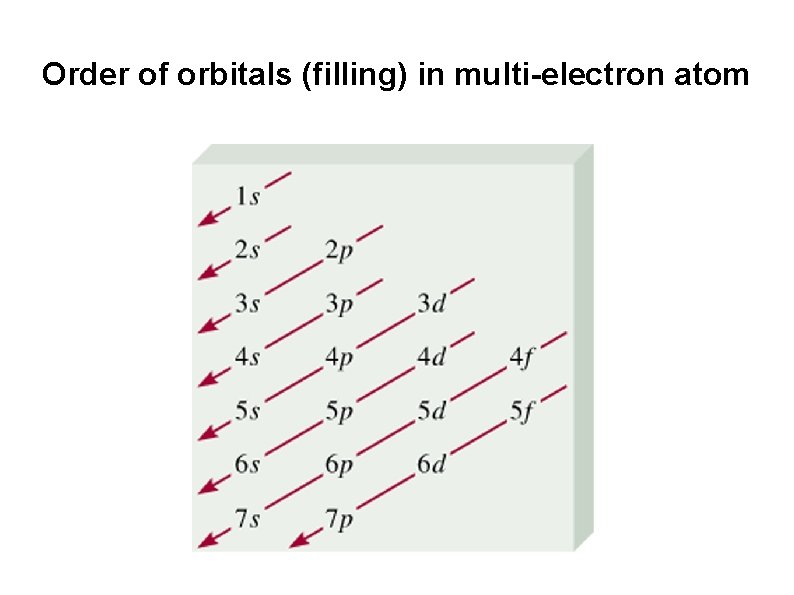
Order of orbitals (filling) in multi-electron atom

Order of orbitals (filling) in multi-electron atom The order of filling orbitals is: 1 s < 2 p < 3 s < 3 p < 4 s < 3 d < 4 p < 5 s Start with the 1 s orbital and move downward, following the arrows. Example: (a) 4 Be (b) 10 Ne Electronic configuration 4 Be : 1 s 2 2 s 2 Electronic configuration 10 Ne : 1 s 2 2 p 6

Pauli Exclusion Principle No two electrons in an atom can have the same four quantum numbers (n, l, m, s). Eg : Li (3 electrons)

Hund’s Rule States that when electrons are added to the orbital of equivalent energy (degenerate orbitals), each orbital are filled singly with electron of the same spin first before it is paired. The electron in half-filled orbitals have the same spins, that is, parallel spins.
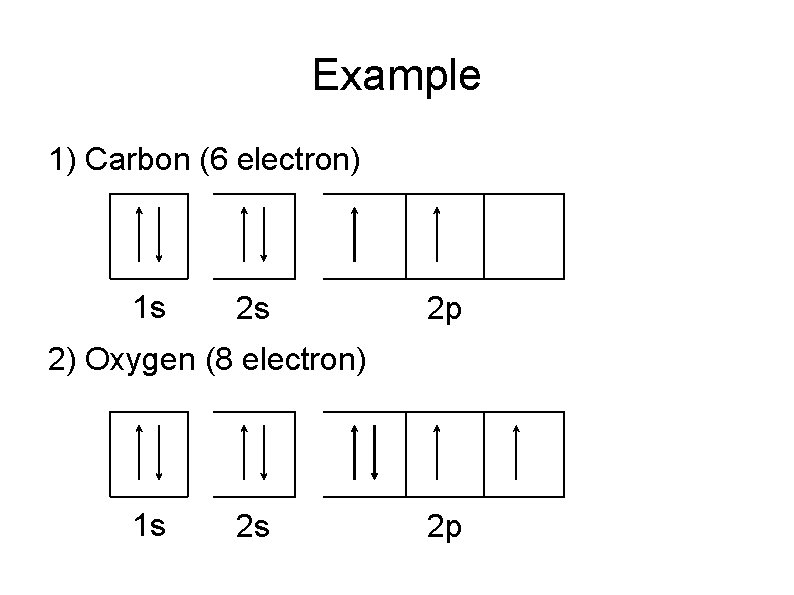
Example 1) Carbon (6 electron) 1 s 2 s 2 p 2) Oxygen (8 electron) 1 s 2 s 2 p

Exercise Write the electronic configuration of the following atom or ion: (a)C (b)Ne (c)Al (d)Al 3+ (e)Cl (f) Cl-

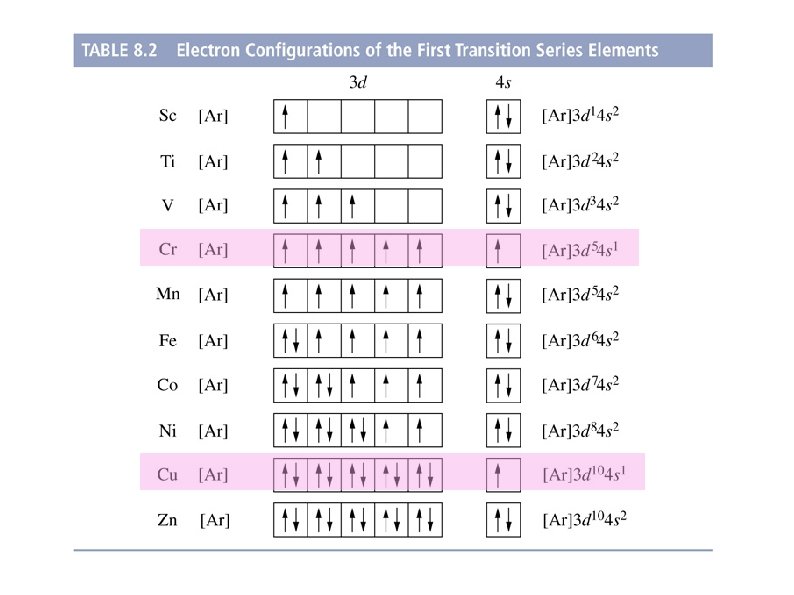
The Anomalous Electronic Configurations of Cr and Cu have electron configurations which are inconsistent with the Aufbau principle. The anomalous are explained on the basis that a filled or half-filled orbital is more stable. Element Expected (Aufbau Principle) Observed/actual Cr (Z=24) 1 s 22 p 63 s 23 p 6 4 s 2 3 d 4 1 s 22 p 63 s 23 p 6 4 s 1 3 d 5 Cu (Z=29) 1 s 22 p 63 s 23 p 6 3 d 9 4 s 2 1 s 22 p 63 s 23 p 6 3 d 10 4 s 1
![Orbital diagram 24 Cr : 18[Ar] 3 d orbital with a half filled orbital Orbital diagram 24 Cr : 18[Ar] 3 d orbital with a half filled orbital](http://slidetodoc.com/presentation_image_h/23c158df63f091c38282ebf8e03b6b37/image-90.jpg)
Orbital diagram 24 Cr : 18[Ar] 3 d orbital with a half filled orbital arrangement are more stable. 24 Cr : 18[Ar] 2 2 s 2 2 p 6 3 s 2 3 p 6 Ar : 1 s 18 *Half filled orbital arrangement increase stability of Cr atom Actual
![Copper expected orbital notation (Aufbau Principle) Cu : 18[Ar] 3 d orbital with fully Copper expected orbital notation (Aufbau Principle) Cu : 18[Ar] 3 d orbital with fully](http://slidetodoc.com/presentation_image_h/23c158df63f091c38282ebf8e03b6b37/image-91.jpg)
Copper expected orbital notation (Aufbau Principle) Cu : 18[Ar] 3 d orbital with fully filled orbital arrangement is more stable. Copper actual orbital notation Cu : 18 [Ar] 2 2 s 2 2 p 6 3 s 2 3 p 6 Ar : 1 s 18

- Slides: 93