CHAPTER 2 ATOMIC STRUCTURE 2 1 Bohrs Atomic

CHAPTER 2 ATOMIC STRUCTURE 2. 1 Bohr’s Atomic Model 2. 2 Quantum Mechanical Model 2. 3 Electronic Configuration 1

LECTURE 1 2. 1 Bohr’s Atomic Model 2

Bohr’s Atomic Model At the end of this topic students should be able to: a) Describe the Bohr’s atomic models. b) Explain the existence of electron energy levels in an atom. c) Calculate the energy of electron using : En = - RH (1/n 2) , RH = 2. 18 x 10 -18 J 3

BOHR’S ATOMIC MODELS In 1913, a young Dutch physicist, Niels Bohr proposed a theory of atom that shook the scientific world. The atomic model he described had electrons circling a central nucleus that contains positively charged protons. Bohr also proposed that these orbits can only occur at specifically “permitted” levels only according to the energy levels of the electron and explain successfully the lines in the hydrogen spectrum. 4

BOHR’S ATOMIC POSTULATES 1. Electron moves in circular orbits about the nucleus. In moving in the orbit, the electron does not radiate any energy and does not absorb any energy. H Nucleus (proton) 1 1 H 5

BOHR’S ATOMIC POSTULATES 2. The energy of an electron in a hydrogen atom is quantised, that is, the electron has only a fixed set of allowed orbits, called stationary states. [ orbit = stationary state = energy level = shell ] H Nucleus (proton) n=1 n=3 n=2 6

BOHR’S ATOMIC POSTULATES 3. At ordinary conditions the electron is at the ground state (lowest level). If energy is supplied, electron absorbed the energy and is promoted from a lower energy level to a higher ones. (Electron is excited) 4. Electron at its excited states is unstable. It will fall back to lower energy level and released a specific amount of energy in the form of light. The energy of the photon equals the energy difference between levels. 7

BOHR’S ATOMIC MODELS 1. Electron moves in circular orbits about the nucleus. In moving in the orbit, the electron does not radiate any energy and does not absorb any energy. 2. The energy of an electron in a hydrogen atom is quantised, that is, the electron has only a fixed set of allowed orbits, called stationary states. [ orbit = stationary state = energy level = shell ] 8

Energy levels in an atom Ground state the state in which the electrons have their lowest energy Excited state the state in which the electrons have shifted from a lower energy level to a higher energy level Energy level energy associated with a specific orbit or state 9

THE ENERGY LEVEL The energy of an electron in its level is given by: RH (Rydberg constant) or A = 2. 18 10 -18 J. n (principal quantum number) = 1, 2, 3 …. (integer) Note: n identifies the orbit of electron Energy is zero if electron is located infinitely far from nucleus Energy associated with forces of attraction are taken to be negative (thus, negative sign) 10

LECTURE 2 At the end of this topic students should be able to: d) Describe the formation of line spectrum of hydrogen atom e) Calculate the energy change of an electron during transition. E = RH (1/n 12 - 1/n 22) , where RH = 2. 18 x 10 -18 J f) Calculate the photon of energy emitted by an electron that produces a particular wavelength during transition E = h where = c/λ 11

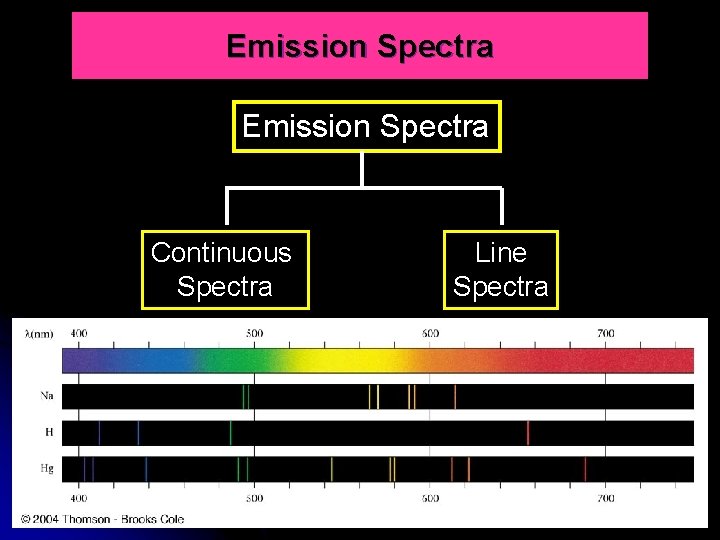
Emission Spectra Continuous Spectra Line Spectra 12

Continuous Spectrum A spectrum consists all wavelength components (containing an unbroken sequence of frequencies) of the visible portion of the electromagnetic spectrum are present. It is produced by incandescent solids, liquids, and compressed gases. 13

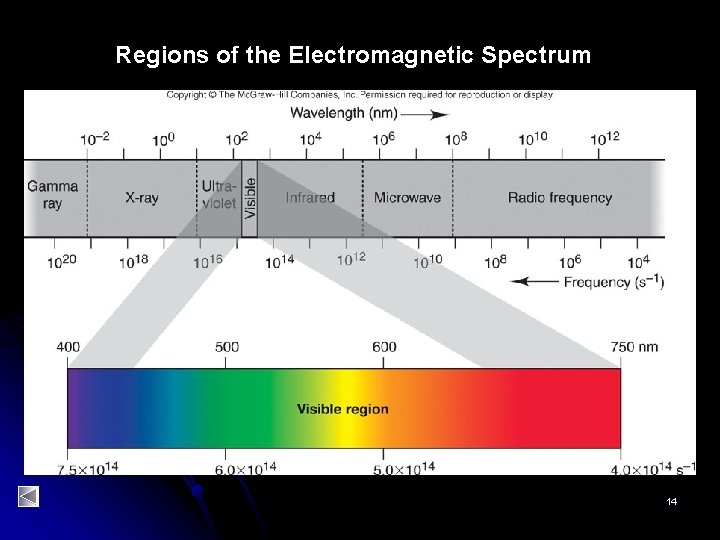
Regions of the Electromagnetic Spectrum 14

FORMATION OF CONTINUOUS SPECTRUM When white light from incandescent lamp is passed through a slit then a prism, it separates into a spectrum. The white light spread out into a rainbow of colours produces a continuous spectrum. The spectrum is continuous in that all wavelengths are presents and each colour merges into the next without a break. 15

Line Spectrum (atomic spectrum) A spectrum consists of discontinuous & discrete lines produced by excited atoms and ions as the electrons fall back to a lower energy level. The radiation emitted is only at a specific wavelength or frequency. It means each line corresponds to a specific wavelength or frequency. Line spectrum are composed of only a few wavelengths giving a series of discrete line separated by blank areas 16

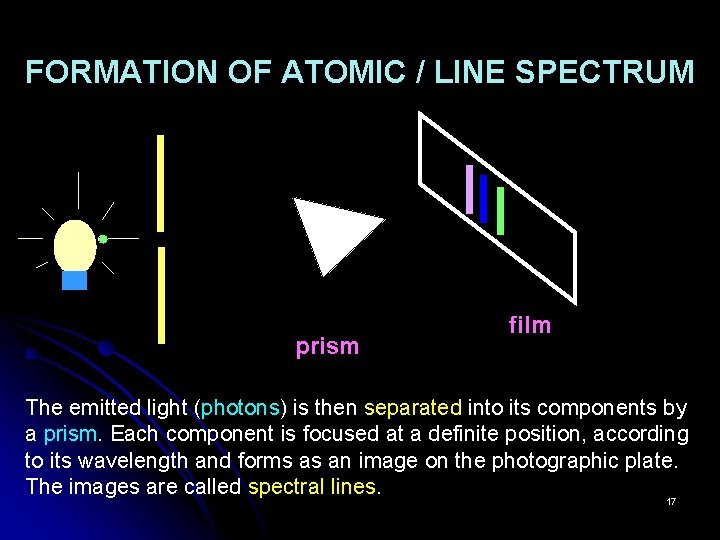
FORMATION OF ATOMIC / LINE SPECTRUM prism film The emitted light (photons) is then separated into its components by a prism. Each component is focused at a definite position, according to its wavelength and forms as an image on the photographic plate. The images are called spectral lines. 17

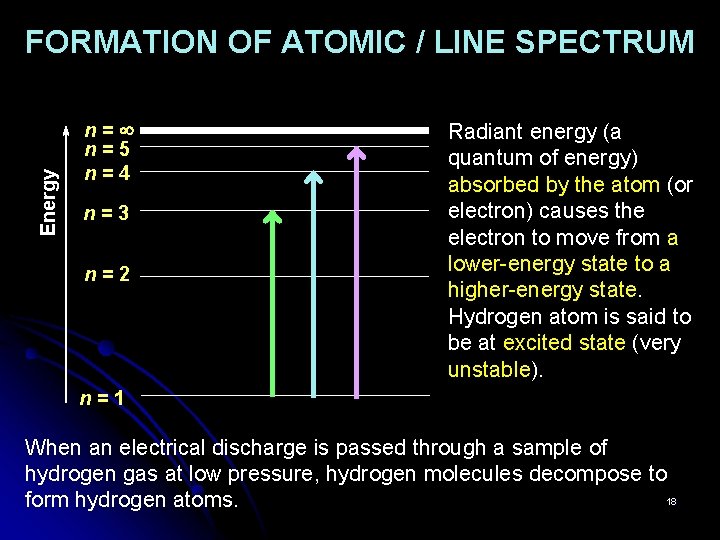
Energy FORMATION OF ATOMIC / LINE SPECTRUM n= n=5 n=4 n=3 n=2 Radiant energy (a quantum of energy) absorbed by the atom (or electron) causes the electron to move from a lower-energy state to a higher-energy state. Hydrogen atom is said to be at excited state (very unstable). n=1 When an electrical discharge is passed through a sample of hydrogen gas at low pressure, hydrogen molecules decompose to 18 form hydrogen atoms.

Energy FORMATION OF ATOMIC / LINE SPECTRUM n= n=6 n=5 n=4 n=3 When the electrons fall back to lower energy levels, radiant energies (photons) are emitted in the form of light (electromagnetic radiation of a particular frequency or wavelength) n=2 Emission of photon 19

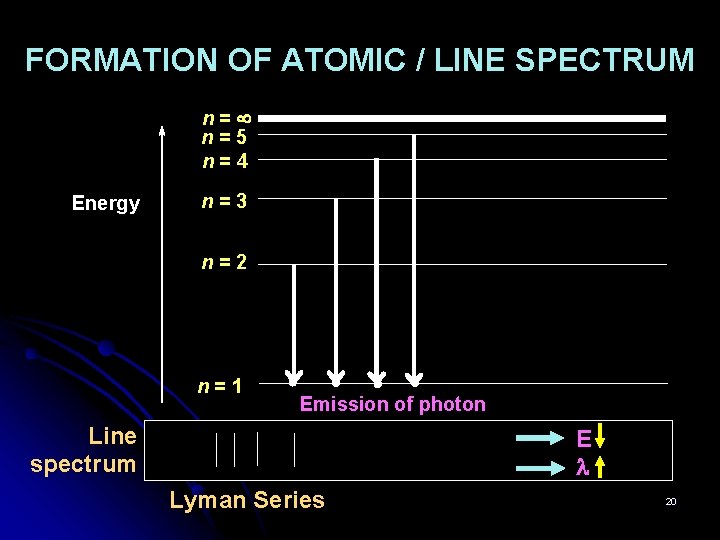
FORMATION OF ATOMIC / LINE SPECTRUM n= n=5 n=4 Energy n=3 n=2 n=1 Emission of photon Line spectrum E Lyman Series 20

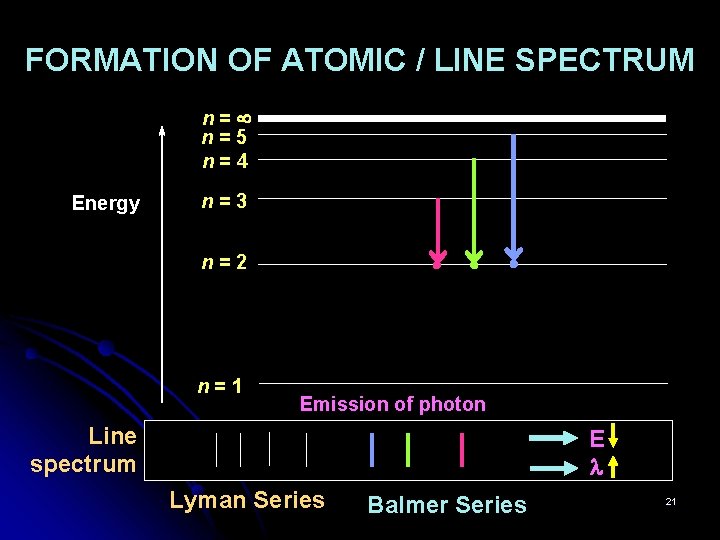
FORMATION OF ATOMIC / LINE SPECTRUM n= n=5 n=4 Energy n=3 n=2 n=1 Emission of photon Line spectrum E Lyman Series Balmer Series 21

Emission series of hydrogen atom n= Pfund series n=4 Brackett series n=3 n=2 Paschen series Balmer series n=1 Lyman series 22

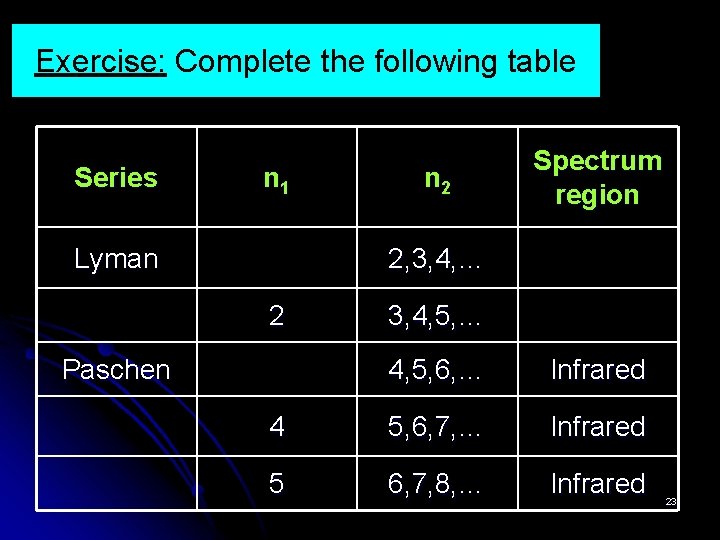
Exercise: Complete the following table Series n 1 Lyman n 2 Spectrum region 2, 3, 4, … 2 Paschen 3, 4, 5, … 4, 5, 6, … Infrared 4 5, 6, 7, … Infrared 5 6, 7, 8, … Infrared 23

Exercise The following diagram depicts the line spectrum of hydrogen atom. Line A is the first line of the Lyman series. A B C D E Line spectrum E Specify the increasing order of the radiant energy, frequency and wavelength of the emitted photon. Which of the line that corresponds to i) the shortest wavelength? ii) the lowest frequency? 24

Exercise W Line spectrum Y Balmer series Describe the transitions of electrons that lead to the lines W, and Y, respectively. Solution 25

Homework Calculate En for n = 1, 2, 3, and 4. Make a onedimensional graph showing energy, at different values of n, increasing vertically. On this graph, indicate by vertical arrows transitions that lead to lines in a) Lyman series b) Paschen series 26

Significance of Atomic Spectra In Lyman series, the frequency of the convergence of spectral lines can be used to find the ionisation energy of hydrogen atom: IE = h The frequency of the first line of the Lyman series > the frequency of the first line of the Balmer series. Line spectrum Balmer Series E Lyman Series 27

Exercise E D Line spectrum C B A Paschen series Which of the line in the Paschen series corresponds to the longest wavelength of photon? Describe the transition that gives rise to the line. Solution 28

Energy calculation Radiant energy emitted when the electron moves from higher-energy state to lower-energy state is given by the difference in energy between energy levels: E = Ef - Ei where Thus, 29

Energy calculation The amount of energy released by the electron is called a photon of energy. A photon of energy is emitted in the form of radiation with appropriate frequency and wavelength. E = h Where; where; h (Planck’s constant) =6. 63 10 -34 J s = frequency c (speed of light) = 3. 00 108 ms-1 Thus, 30

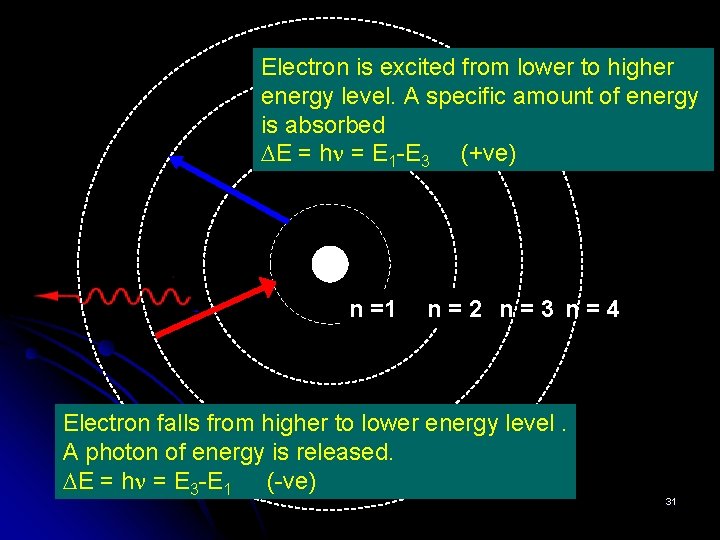
Electron is excited from lower to higher energy level. A specific amount of energy is absorbed E = h = E 1 -E 3 (+ve) n =1 n=2 n=3 n=4 Electron falls from higher to lower energy level. A photon of energy is released. E = h = E 3 -E 1 (-ve) 31

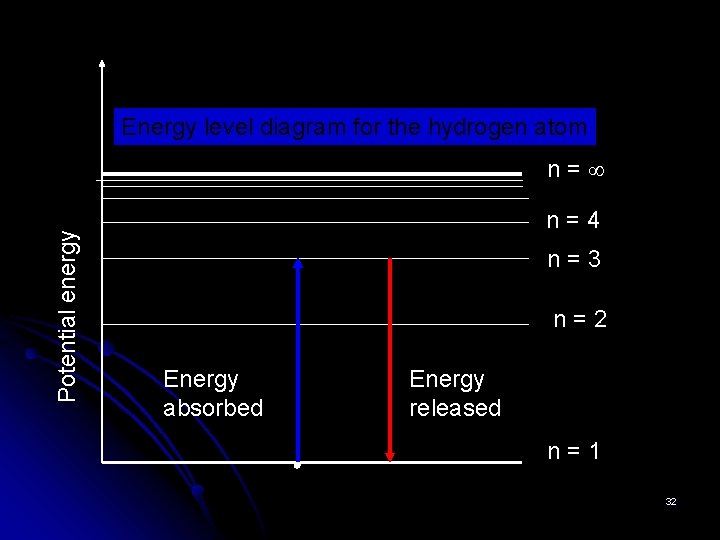
Energy level diagram for the hydrogen atom Potential energy n= n=4 n=3 n=2 Energy absorbed Energy released n=1 32

Exercises: 1) Calculate the energy of an electron in the second energy level of a hydrogen atom. (-5. 448 x 10 -19 J) 2) Calculate the energy of an electron in the energy level n = 6 of an hydrogen atom. 3) Calculate the energy change (J), that occurs when an electron falls from n = 5 to n = 3 energy level in a hydrogen atom. (answer: 1. 55 x 10 -19 J) 4) Calculate the frequency and wavelength (nm) of the radiation emitted in question 3. 33

LECTURE 3 At the end of this topic students should be able to: g) Perform calculations involving the Rydberg equation for Lyman, Balmer, Paschen, Brackett and Pfund series. 1/ λ = RH (1/n 12 - 1/n 22) , where RH = 1. 097 x 107 m-1 and n 1<n 2 h) Calculate the ionisation energy of hydrogen atom from Lyman series. i) State the weaknesses of Bohr’s atomic model. j) State the dual nature of electron using the Broglie’s postulate and Hesseinberg’s uncertainty principle. 34

Rydberg Equation Wavelength emitted by the transition of electron between two energy levels is calculated using Rydberg equation: æ 1 ö 1 1 = R H çç 2 2 λ è n 1 n 2 ø where RH = 1. 097 107 m-1 = wavelength Since should have a positive value thus n 1 < n 2 35

Example Calculate the wavelength, in nanometers of the spectrum of hydrogen corresponding to ni = 2 and nf = 4 in the Rydberg equation. Solution: Rydberg equation: 1/λ = RH (1/ni 2 – 1/nf 2) ni = 2 nf = 4 RH = 1. 097 x 10 m 7 1/λ = RH (1/22 – 1/42) = RH(1/4 -1/16) λ = 4. 86 m x 102 m = 486 nm 36

Example Use the Rydberg equation to calculate the wavelength of the spectral line of hydrogen atom that would result when an electron drops from the fourth orbit to the second orbit, then identified the series the line would be found. Solution: 1/λ = RH (1/n 1 2 – 1/n 2 2) n 1 = 2 n 2 = 4 1/λ = 1. 097 x 107 (1/22 – 1/42) λ = 4. 86 x 10 -7 m = 486 nm *e dropped to the second orbit (n=2), >>> Balmer series 37

EXAMPLE 3 Calculate the wavelengths of the fourth line in the Balmer series of hydrogen. n 1 = 2 n 2 = 6 RH = 1. 097 x 107 m-1 1 λ λ = RH 1 1 22 62 = 4. 10 x 10 -7 m 38

Different values of RH and its usage 1. RH = 1. 097 107 m-1 1 λ = RH 1 1 n 12 n 22 n 1 < n 2 RH = 2. 18 x 10 -18 J 39

EXAMPLE 4 Calculate the energy liberated when an electron from the fifth energy level falls to the second energy level in the hydrogen atom. 1 λ = RH 1 =1. 097 x 107 λ 1 1 n 12 n 22 1 1 22 52 ΔE = (6. 63 10 -34 Js)X(3. 00 108 ms-1) X (0. 2303 X 107 m-1) m-1 ΔE = 4. 58 x 10 -19 J = 0. 2303 X 107 40

EXERCISE Calculate what is; i ) Wavelength ii ) Frequency iii ) Wave number of the last line of hydrogen spectrum in Lyman series Wave number = 1/wavelength For Lyman series; n 1 = 1 & n 2 = ∞ Ans: i. 9. 116 x 10 -8 m ii. 3. 29 x 1015 s-1 iii. 1. 0970 X 107 m-1 41

Ionization Energy Definition : Ionization energy is the minimum energy required to remove one mole of electron from one mole of gaseous atom/ion. M (g) M+ (g) + e H = +ve The hydrogen atom is said to be ionised when electron is removed from its ground state (n = 1) to n = . At n = , the potential energy of electron is zero, here the nucleus attractive force has no effect on the electron (electron is free from nucleus). 42

Example n 1 = 1, n 2 = ∞ ∆E = RH (1/n 12 – 1/n 22) = 2. 18 X 10 -18 (1/12 – 1/ ∞ 2) = 2. 18 X 10 -18 (1 – 0) = 2. 18 X 10 -18 J Ionisation energy = 2. 18 X 10 -18 x 6. 02 X 1023 J mol-1 =1. 312 x 106 J mol-1 = 1312 k. J mol-1 43

Finding ionisation energy experimentally: Convergent limit 1 st line 1 Ionisation energy is determined by detecting the wavelength of the convergence point 44

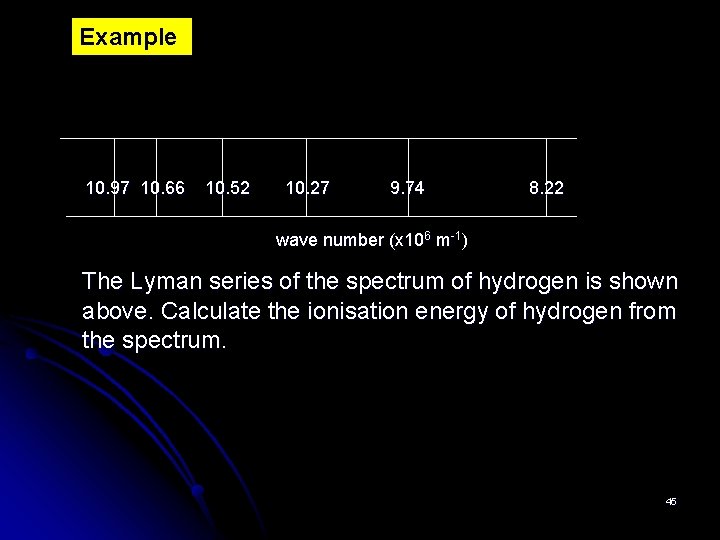
Example 10. 97 10. 66 10. 52 10. 27 9. 74 8. 22 wave number (x 106 m-1) The Lyman series of the spectrum of hydrogen is shown above. Calculate the ionisation energy of hydrogen from the spectrum. 45

Solution ΔE = hc/λ =h x c / λ = h x c x wave no. = 6. 626 x 10 -34 J s x 3 x 108 m s-1 x 10. 97 x 106 m-1 = 218. 06 x 10 -20 J = 2. 18 x 10 -18 J Ionisation energy = 2. 18 X 10 -18 x 6. 02 X 1023 J mol-1 =1. 312 x 106 J mol-1 = 1312 k. J mol-1 46

Exercise Compute the ionisation energy of hydrogen atom in k. J mol 1. Solution J 47

The weakness of Bohr’s Theory 1. His theory could not be extended to predict the energy levels and spectra of atoms and ions with more than one electron. It only can explain the hydrogen spectrum or ions contain one electron eg He+, Li 2+. 2. Electrons are restricted to orbit the nucleus at certain fixed distances 3. It cannot explain for the dual nature of electron 4. It cannot explain for the extra lines formed in the hydrogen spectrum. 48

Point to Ponder Davisson & Germer observed the diffraction of electrons when a beam of electrons was directed at a nickel crystal. Diffraction patterns produced by scattering electrons from crystals are very similar to those produced by scattering X-rays from crystals. This experiment demonstrated that electrons do indeed possess wavelike properties. Thus, can the ‘position’ of a wave be specified? ? ? specified 49

de Broglie’s Postulate In 1924 Louis de Broglie proposed that not only light but all matter has a dual nature and possesses both wave and corpuscular properties. De Broglie deduced that the particle and wave properties are related by the expression: h = m h = Planck constant (J s) m = particle mass (kg) = velocity (m/s) = wavelength of a matter wave 50

Heisenberg’s Uncertainty Principle It is impossible to know simultaneously both the momentum p (defined as mass times velocity) and the position of a particle with certain. Stated mathematically, h x p 4 where x = uncertainty in measuring the position p = uncertainty in measuring the momentum = mv h = Planck constant 51

LECTURE 4 2. 2 QUANTUM MECHANICAL MODEL 52

At the end of this topic students should be able to: a) Define the term orbital. b) State the four quantum numbers of an electron in an orbital (n, , m, s). i) principal quantum number, n ii) angular momentum quantum number, iii) magnetic quantum number, m iv) electron spin quantum number, s. 53

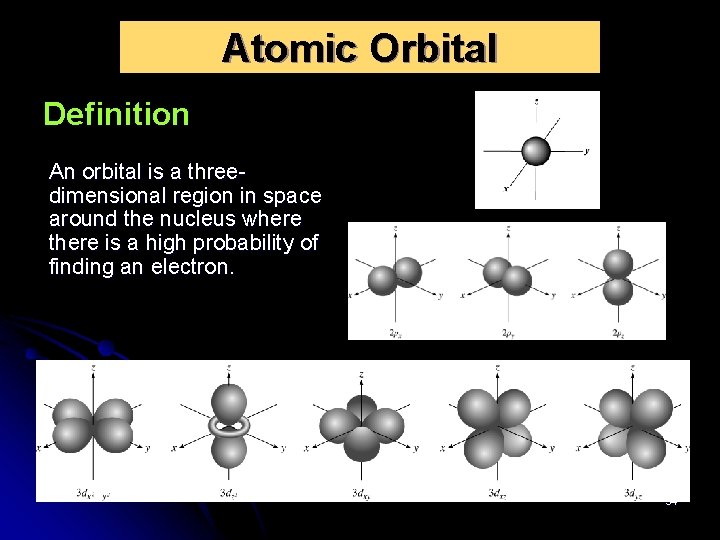
Atomic Orbital Definition An orbital is a threedimensional region in space around the nucleus where there is a high probability of finding an electron. 54

Quantum Numbers Each of the electrons in an atom is described and characterised by a set of four quantum numbers, namely a) principal quantum number, n b) angular momentum quantum number, c) magnetic quantum number, m d) electron spin quantum number, s. 55

Principal Quantum Number, n The value of n determines the energy of an orbital and thereby the energy of the electron in that particular orbital. The principal quantum number may have only integral values: n =1, 2, 3, …, . n 1 2 3 4 shell K L M N Orbital size Energy increases 56

Angular Momentum Quantum Number, - Alternative name: Subsidiary / Azimuthal / Orbital Quantum Number - The value of indicates the shape of the atomic orbital (AO), the types of orbitals, and the angular momentum of the electron. - The allowed values of are 0, 1, 2, …, (n 1) Letters are assigned to different numerical values of . Numerical value of Symbol Orbital shape 0 1 s p spherical dumbbell 2 3 d f cloverleaf 57

Angular Momentum Quantum Number, - is dependant on n. (i. e. , 0 < n). If n = 1, can only be 0 (s-orbital) If n = 2, can be 0 or 1 giving rise to two subshells (s and p-orbitals) of slightly different energy. If n = 3, can be 0, 1, or 2 (there are three subshells: (s, p, and d-orbitals) 58

Magnetic Quantum Number, m The direction or orientation of the magnetic field is determined by the value of m. Possible values of m depend on the value of . For a given , m can be : , …, 0, …, + ( m + ) If = 0, m can only be 0 one orbital in s-subshell If = 1, m can be 1, 0, +1 three orbitals in p-subshell If = 2, m can be 2, 1, 0, +1, +2 five orbitals in d-subshell 59

Magnetic Quantum Number, m The number of m values indicates the number of orbitals in a subshell with a particular value. The values of n = 2 and = 1 indicate that we have a 2 psubshell, and in this subshell we have three 2 p-orbitals (because there are three values of m, given by -1, 0 and +1) 60

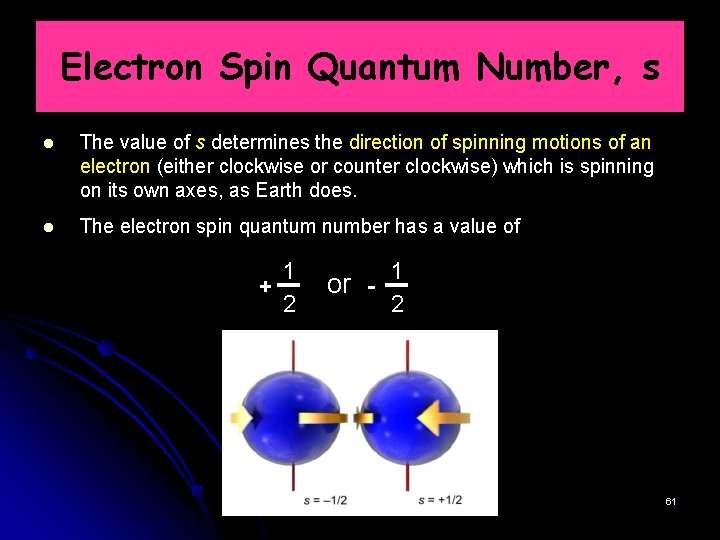
Electron Spin Quantum Number, s The value of s determines the direction of spinning motions of an electron (either clockwise or counter clockwise) which is spinning on its own axes, as Earth does. The electron spin quantum number has a value of 1 + 2 1 or 2 61

Points to Remember Atomic orbitals with the same energy (i. e. , the same value of n and ) are said to be degenerated. Therefore, there are (2 +1) degenerate orbitals for each value of . The maximum number of electrons in a particular energy level, n is given by the expression as follows: max no. of e = 2 n 2 62

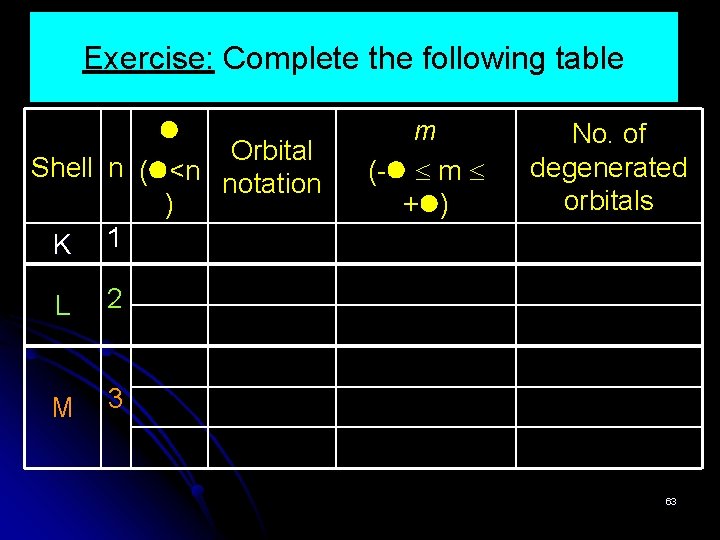
Exercise: Complete the following table Orbital Shell n ( <n notation ) K 1 L 2 M 3 m (- m + ) No. of degenerated orbitals 63

Exercise State whether or not each of the following symbols is an acceptable designation for an atomic orbital. Explain what is wrong with the unacceptable symbols. a) 2 d b) 6 g c) 7 s d) 5 i 64

LECTURE 5 At the end of this topic students should be able to: - c) Sketch the shapes of s, p and d orbitals with the correct orientations. 65

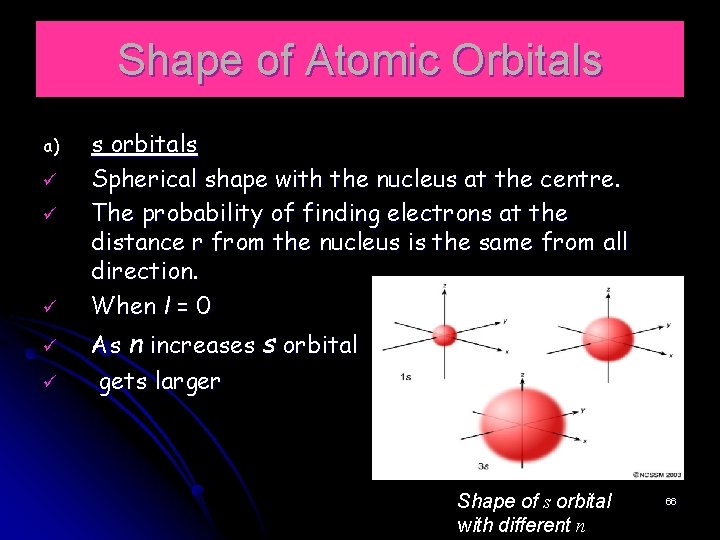
Shape of Atomic Orbitals a) ü ü ü s orbitals Spherical shape with the nucleus at the centre. The probability of finding electrons at the distance r from the nucleus is the same from all direction. When l = 0 As n increases s orbital gets larger Shape of s orbital with different n 66

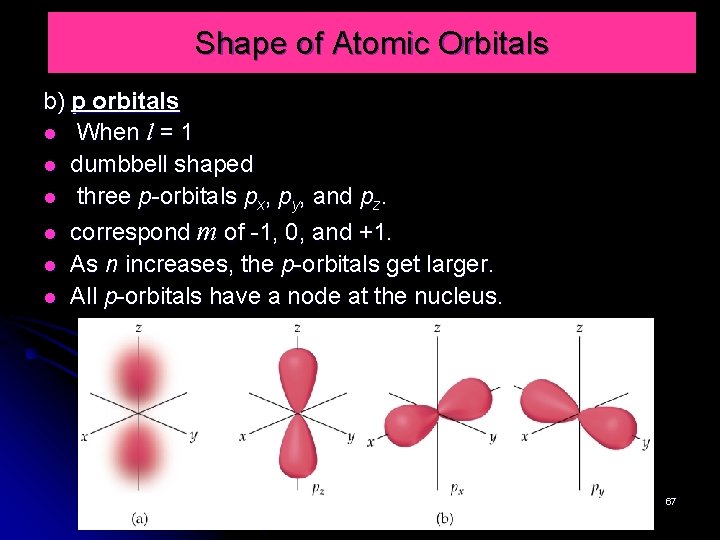
Shape of Atomic Orbitals b) p orbitals When l = 1 dumbbell shaped three p-orbitals px, py, and pz. correspond m of -1, 0, and +1. As n increases, the p-orbitals get larger. All p-orbitals have a node at the nucleus. 67

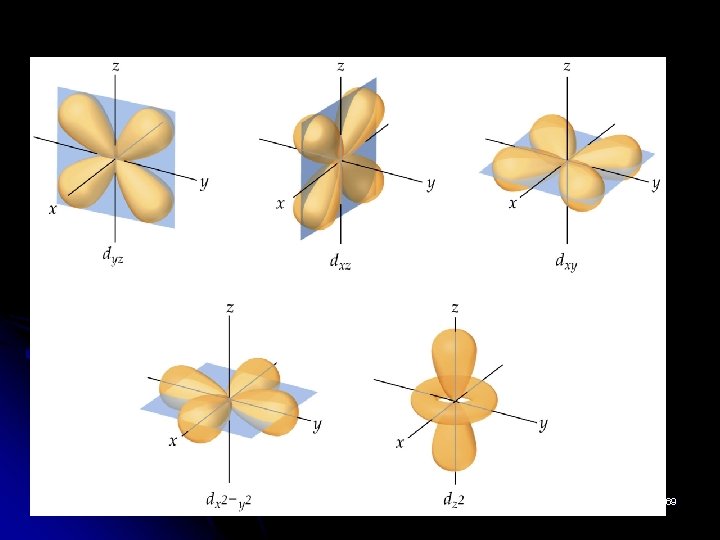
Shape of Atomic Orbitals § shape; four d orbitals have four lobes (perpendicular), one d orbital has two major lobes along z axis and a donut-shaped girdles the centre. § When l = 2 m = -2, -1, 0, 1, 2 § the orbitals are: dyz, dxy, dx 2 -y 2, dz 2 68

69

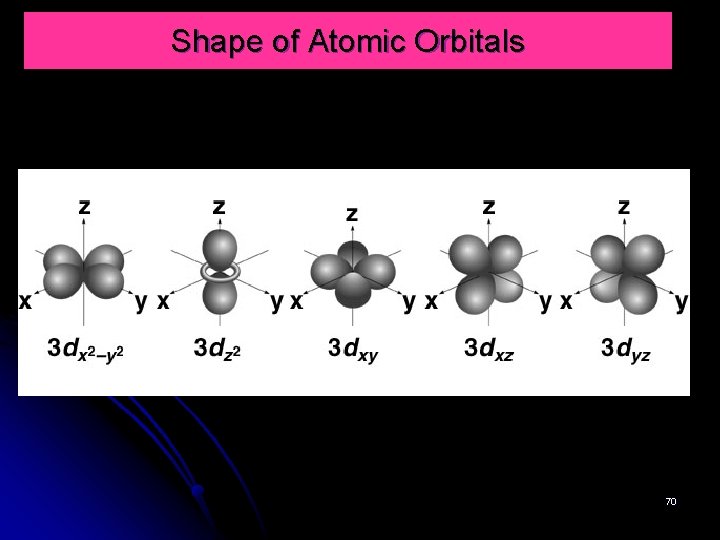
Shape of Atomic Orbitals 70

LECTURE 6 & 7 2. 3 ELECTRONIC CONFIGURATION 71

Electronic Configuration At the end of this topic students should be able to: a) State and use Aufbau principle, Hund’s rule and Pauli exclusion principle b) Apply rules in (a) to fill electrons into atomic orbitals. c) Write the electronic configuration of an atom and monostomic ions by using spdf notation. d) Explain the anomalous electronic configurations of chromium and copper. 72

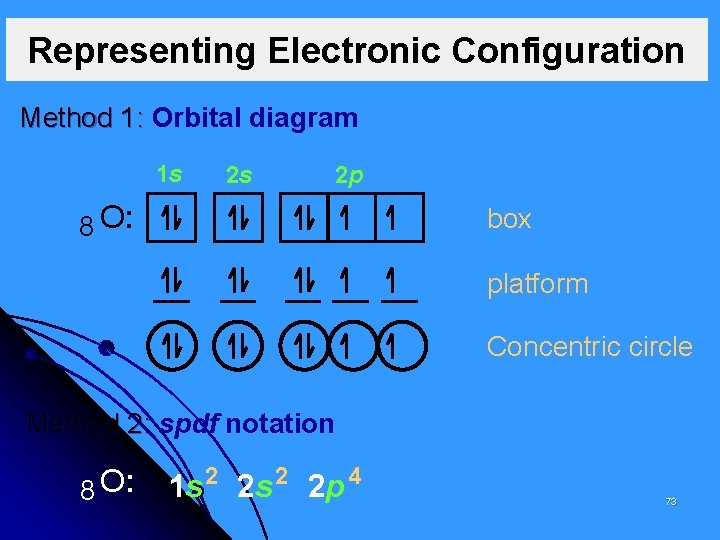
Representing Electronic Configuration Method 1: Orbital diagram 1 s 2 s 2 p 8 O: box platform Concentric circle Method 2: spdf notation 8 O: 1 s 2 2 p 4 73

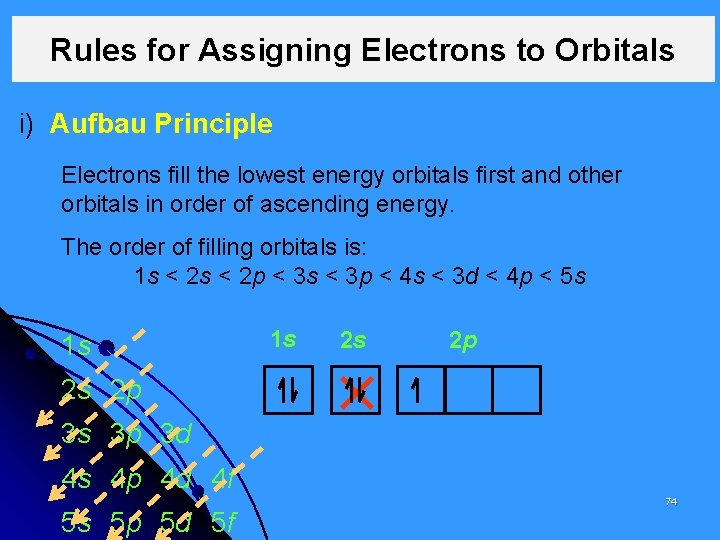
Rules for Assigning Electrons to Orbitals i) Aufbau Principle Electrons fill the lowest energy orbitals first and other orbitals in order of ascending energy. The order of filling orbitals is: 1 s < 2 p < 3 s < 3 p < 4 s < 3 d < 4 p < 5 s 1 s 1 s 2 s 2 p 3 s 3 p 3 d 4 s 4 p 4 d 4 f 5 s 5 p 5 d 5 f 74

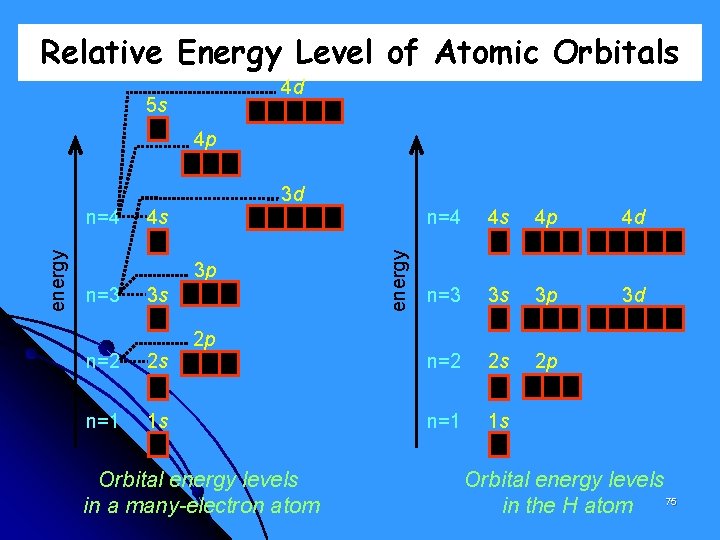
Relative Energy Level of Atomic Orbitals 4 d 5 s 4 p 3 d 4 s 3 p n=3 3 s n=2 2 s n=1 1 s 2 p Orbital energy levels in a many-electron atom energy n=4 4 s 4 p 4 d n=3 3 s 3 p 3 d n=2 2 s 2 p n=1 1 s Orbital energy levels 75 in the H atom

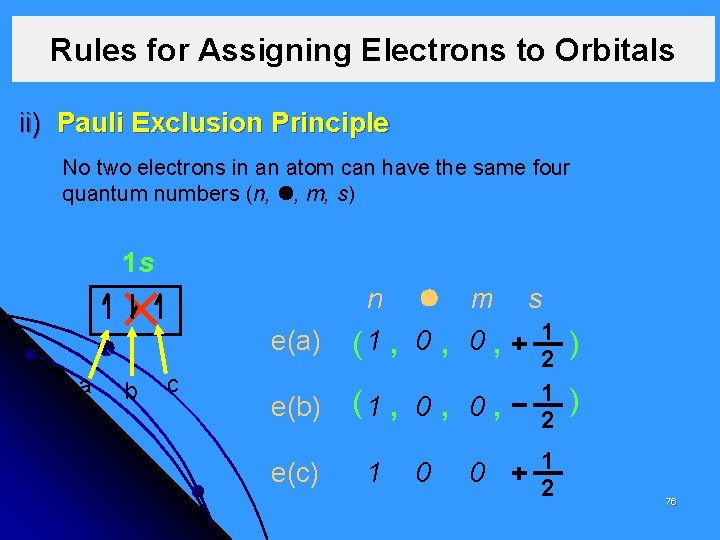
Rules for Assigning Electrons to Orbitals ii) Pauli Exclusion Principle No two electrons in an atom can have the same four quantum numbers (n, , m, s) 1 s a b c e(a) n m s 1 1 0 0 ( , , , 2 ) e(b) (1 , 0 , e(c) 1 0 0 1 2 ) 76

Rules for Assigning Electrons to Orbitals iii) Hund’s Rule Only when all the degenerate orbitals (a group of orbitals of identical energy e. g. three p-orbitals and five dorbitals) contain an electron do the electrons begin to occupy these orbitals in pairs. The electrons in half-filled orbitals have the same spins, that is, parallel spins. 2 p 77

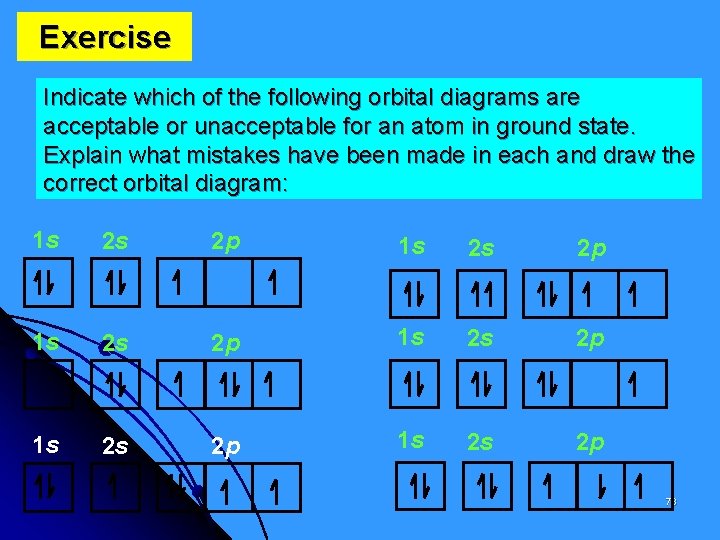
Exercise Indicate which of the following orbital diagrams are acceptable or unacceptable for an atom in ground state. Explain what mistakes have been made in each and draw the correct orbital diagram: 1 s 2 s 2 p 1 s 2 s 2 p 78

Exercise Draw ‘electrons-in-boxes’ diagram of the electronic configuration of titanium, Ti (Z = 22). Also, write the groundstate electronic configurations for Ti and Ti 2+ ion. 79

IMPORTANT! In an empty atom, the 4 s orbital has a lower energy compared to that of the 3 d orbital. That is why electrons fill the 4 s orbital first before filling the 3 d orbital. However, once electron/s is/are added to the 3 d orbital, the 4 s electrons are repelled to a higher energy level. The 3 d orbitals now have lower energy than 4 s. 80

Points to remember The electronic configuration of atom or monatomic ion at ground state Distribution of electrons obeys Aufbau principle, Pauli exclusion principle and Hund’s rule Each atomic orbital can only accommodate a maximum of 2 electrons Atomic orbital is a 3 -D region in space around the nucleus where there is a high probability of finding an electron. Assigning electrons to subshells s-orbital a max of 2 electrons (ns 2) p-orbitals a max of 6 electrons (np 6) d-orbitals a max of 10 electrons (nd 10) 81

The Anomalous Electronic Configurations of Cr and Cu have electron configurations which are inconsistent with the Aufbau principle. The anomalous are explained on the basis that a filled or half-filled orbital is more stable. Element Expected Observed/actual Cr (Z=24) [Ar] 3 d 4 4 s 2 [Ar] 3 d 5 4 s 1 Cu (Z=29) [Ar] 3 d 9 4 s 2 [Ar] 3 d 10 4 s 1 82

Chromium predicted orbital notation 24 Cr : 18[Ar] 3 d 4 s The actual orbital notation 24 Cr : 18[Ar] 3 d 4 s Half filled orbital is more stable (possesses an extra, added stability) 83

Copper predicted orbital notation Ø Cu : [Ar] 3 d 4 s The actual orbital notation Ø Cu : [Ar] 3 d Full filled orbital is more stable (possesses an extra, added stability) 4 s 84

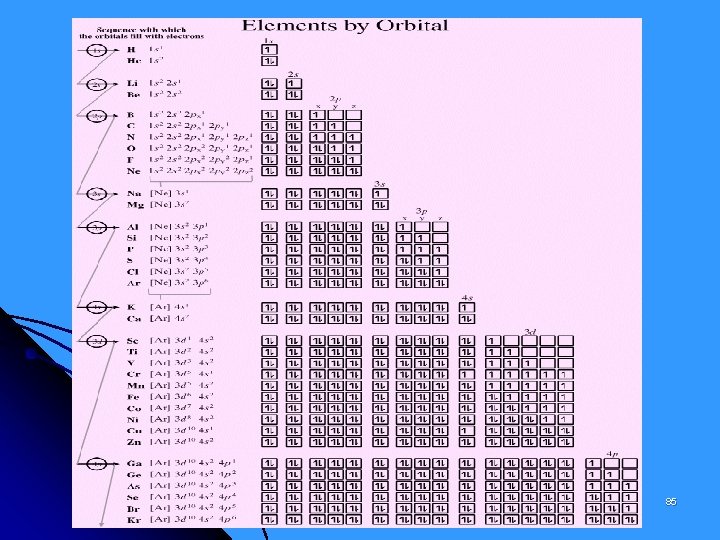
z = 21 z = 30 85

Exercise Write the ground-state electronic configuration and explain the anomalous case for Cr (Z=24) and Cu ( Z=29) 86

Writing Electronic Configuration for Negative Ion Add electron according to Aufbau Principle. Example: i. Cl- ii. O 2 -

Writing Electronic Configuration for Positive Ions Remove electron from the outermost orbital (largest value of n) Example: i. Mg 2+ ii. K+ iii. Fe 2+