Chapter 2 Algorithm Analysis All sections 1 Complexity

Chapter 2 Algorithm Analysis All sections 1

Complexity Analysis • Measures efficiency (time and memory) of algorithms and programs – Can be used for the following • Compare different algorithms • See how time varies with size of the input • Operation count – Count the number of operations that we expect to take the most time • Asymptotic analysis – See how fast time increases as the input size approaches infinity 2

Operation Count Examples Example 1 for(i=0; i<n; i++) cout << A[i] << endl; Number of output = n Example 3: Triangular matrixvector multiplication pseudocode ci 0, i = 1 to n for j = 1 to i ci += aij bj; Number of multiplications = i=1 n i = n(n+1)/2 �� Example 2 template <class T> bool Is. Sorted(T *A, int n) { bool sorted = true; for(int i=0; i<n-1; i++) if(A[i] > A[i+1]) sorted = false; return sorted; } Number of comparisons = n - 1 3

Scaling Analysis • How much will time increase in example 1, if n is doubled? – t(2 n)/t(n) = 2 n/n = 2 • Time will double • If time t(n) = 2 n 2 for some algorithm, then how much will time increase if the input size is doubled? – t(2 n)/t(n) = 2 (2 n)2 / (2 n 2) = 4 n 2 / n 2 = 4 4

Comparing Algorithms • Assume that algorithm 1 takes time t 1(n) = 100 n+n 2 and algorithm 2 takes time t 2(n) = 10 n 2 – If an application typically has n < 10, then which algorithms is faster? – If an application typically has n > 100, then which algorithms is faster? • Assume algorithms with the following times – Algorithm 1: insert - n, delete - log n, lookup - 1 – Algorithm 2: insert - log n, delete - n, lookup - log n • Which algorithm is faster if an application has many inserts but few deletes and lookups? 5

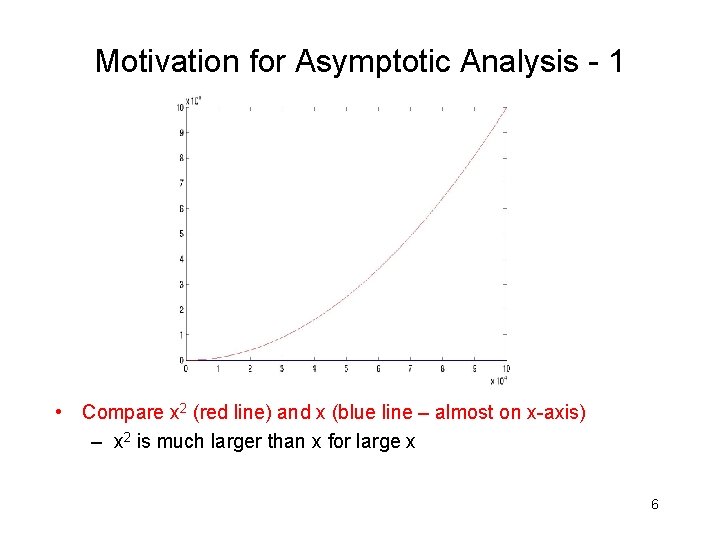
Motivation for Asymptotic Analysis - 1 • Compare x 2 (red line) and x (blue line – almost on x-axis) – x 2 is much larger than x for large x 6

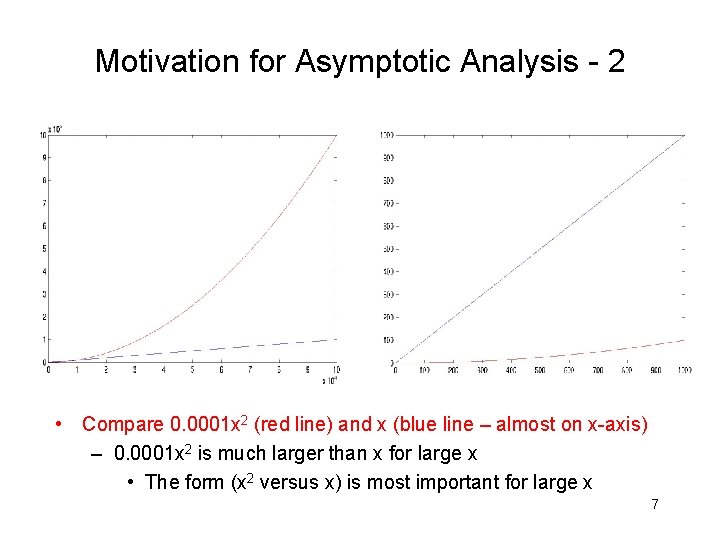
Motivation for Asymptotic Analysis - 2 • Compare 0. 0001 x 2 (red line) and x (blue line – almost on x-axis) – 0. 0001 x 2 is much larger than x for large x • The form (x 2 versus x) is most important for large x 7

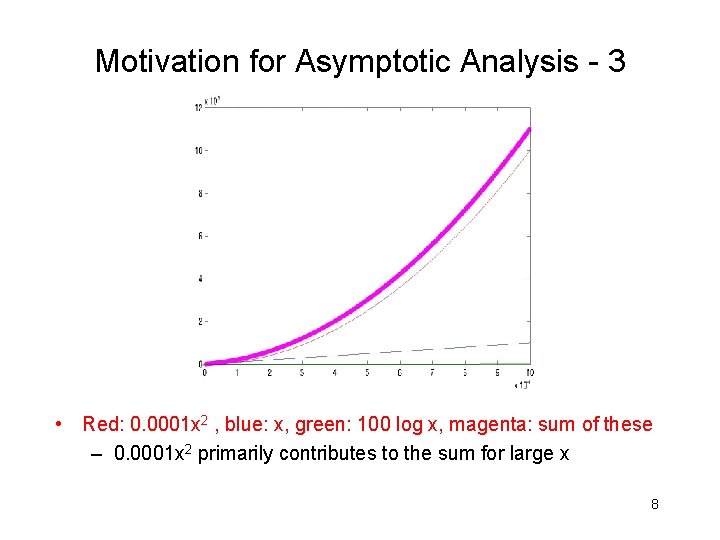
Motivation for Asymptotic Analysis - 3 • Red: 0. 0001 x 2 , blue: x, green: 100 log x, magenta: sum of these – 0. 0001 x 2 primarily contributes to the sum for large x 8

Asymptotic Complexity Analysis • Compares growth of two functions – T = f(n) – Variables: nonnegative integers • For example, size of input data – Values: non-negative real numbers • For example, running time of an algorithm • Independent of – constant multipliers – and lower-order effects • Metrics – “Big O” Notation: O() – “Big Omega” Notation: () – “Big Theta” Notation: Θ() • Dependent on – Eventual (asymptotic) behavior 9

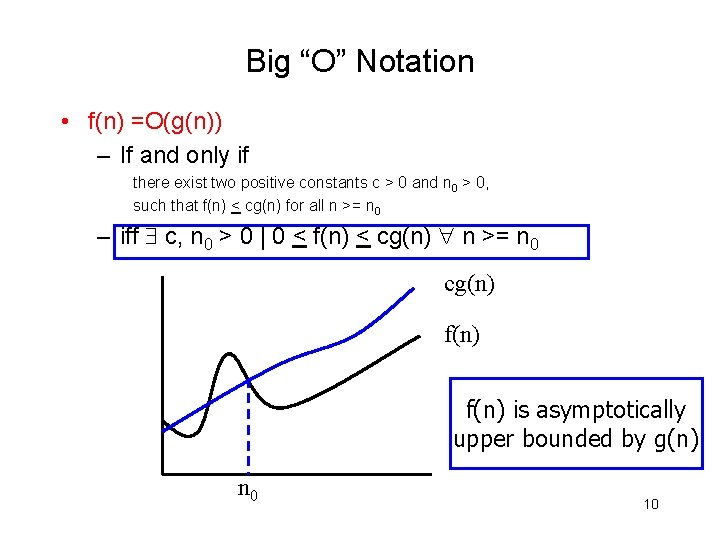
Big “O” Notation • f(n) =O(g(n)) – If and only if there exist two positive constants c > 0 and n 0 > 0, such that f(n) < cg(n) for all n >= n 0 – iff c, n 0 > 0 | 0 < f(n) < cg(n) n >= n 0 cg(n) f(n) is asymptotically upper bounded by g(n) n 0 10

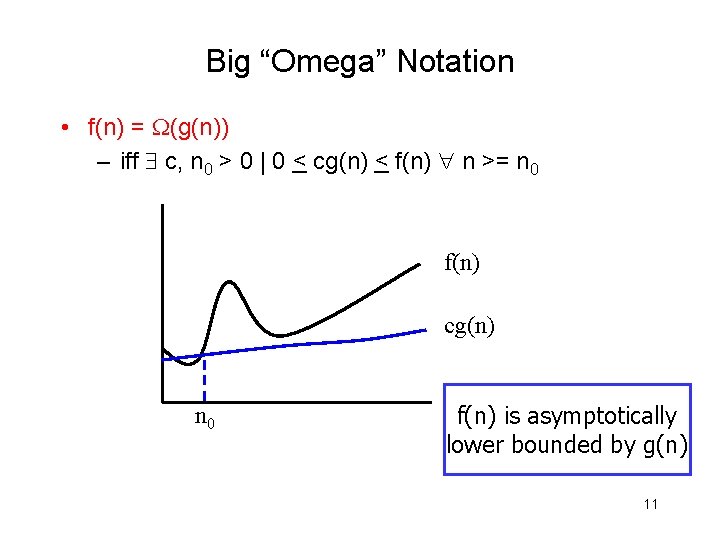
Big “Omega” Notation • f(n) = (g(n)) – iff c, n 0 > 0 | 0 < cg(n) < f(n) n >= n 0 f(n) cg(n) n 0 f(n) is asymptotically lower bounded by g(n) 11

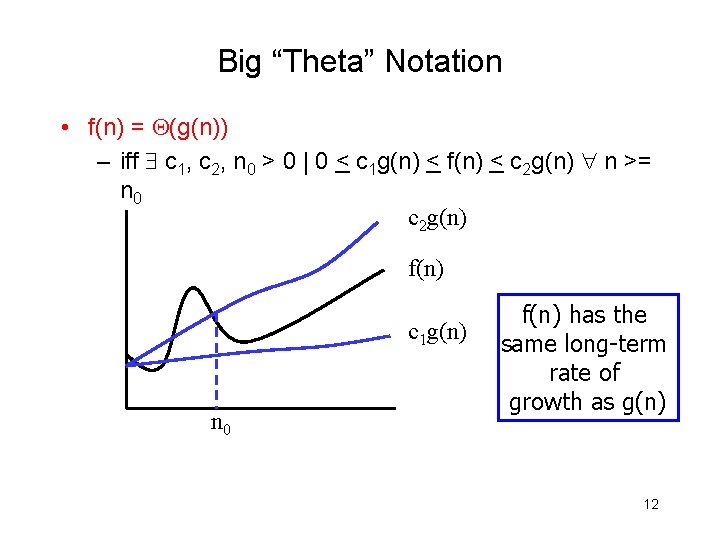
Big “Theta” Notation • f(n) = (g(n)) – iff c 1, c 2, n 0 > 0 | 0 < c 1 g(n) < f(n) < c 2 g(n) n >= n 0 c 2 g(n) f(n) c 1 g(n) n 0 f(n) has the same long-term rate of growth as g(n) 12

Examples f(n) = 3 n 2 + 17 • (1), (n 2) lower bounds • O(n 2), O(n 3), … upper bounds • (n 2) exact bound f(n) = 1000 n 2 + 17 + 0. 001 n 3 • (? ) lower bounds • O(? ) upper bounds • (? ) exact bound 13

Analogous to Real Numbers • f(n) = O(g(n)) • f(n) = (g(n)) (a < b) (a > b) (a = b) • The above analogy is not quite accurate, but its convenient to think of function complexity in these terms. 14

Transitivity • • f(n) = O(g(n)) (a < b) f(n) = (g(n)) (a > b) f(n) = (g(n)) (a = b) If f(n) = O(g(n)) and g(n) = O(h(n)) – Then f(n) = O(h(n)) • If f(n) = (g(n)) and g(n) = (h(n)) – Then f(n) = (h(n)) • And many other properties 15

Some Rules of Thumb • If f(x) is a polynomial of degree k – Then f(x) = (xk) • logk. N = O(N) for any constant k – Logarithms grow very slowly compared to even linear growth 16

Typical Growth Rates 17

Exercise • f(N) = N log. N and g(N) = N 1. 5 – Which one grows faster? ? • Note that g(N) = N 1. 5 = N*N 0. 5 – Hence, between f(N) and g(N), we only need to compare growth rate of log N and N 0. 5 – Equivalently, we can compare growth rate of log 2 N with N – Now, refer to the result on the last slide to figure out whether f(N) or g(N) grows faster! 18

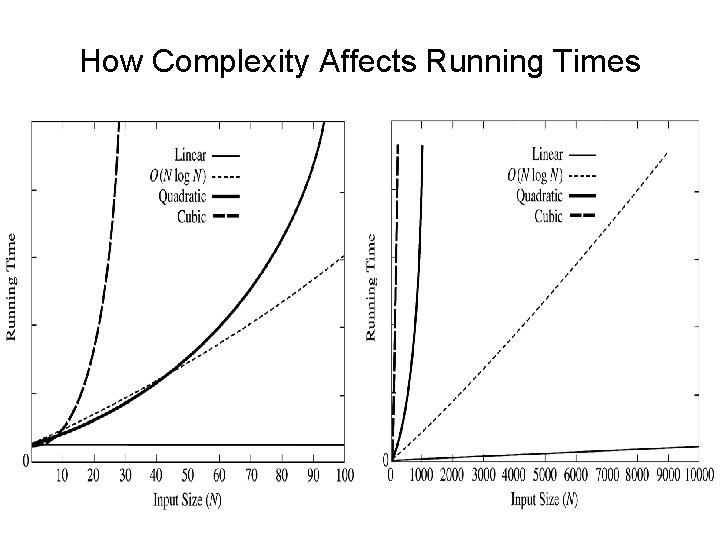
How Complexity Affects Running Times 19

Running Time Calculations - Loops for (j = 0; j < n; ++j) { // 3 atomics } • Number of atomic operations – Each iteration has 3 atomic operations, so 3 n – Cost of the iteration itself • One initialization assignment • n increment (of j) • n comparisons (between j and n) • Complexity = (3 n) = (n) 20

Loops with Break for (j = 0; j < n; ++j) { // 3 atomics if (condition) break; } • • Upper bound = O(4 n) = O(n) Lower bound = Ω(4) = Ω(1) Complexity = O(n) Why don’t we have a (…) notation here? 21

Sequential Search • Given an unsorted vector a[ ], find the location of element X. for (i = 0; i < n; i++) { if (a[i] == X) return true; } return false; • Input size: n = a. size() • Complexity = O(n) 22

If-then-else Statement if(condition) i = 0; else for ( j = 0; j < n; j++) a[j] = j; • Complexity = ? ? = O(1) + max ( O(1), O(N)) = O(1) + O(N) = O(N) 23

Consecutive Statements • Add the complexity of consecutive statements for (j = 0; j < n; ++j) { // 3 atomics } for (j = 0; j < n; ++j) { // 5 atomics } • Complexity = (3 n + 5 n) = (n) 24

Nested Loop Statements • Analyze such statements inside out for (j = 0; j < n; ++j) { // 2 atomics for (k = 0; k < n; ++k) { // 3 atomics } } • Complexity = ((2 + 3 n)n) = (n 2) 25

Recursion long factorial( int n ) { if( n <= 1 ) return 1; else return n*factorial(n- 1); } In terms of big-Oh: t(1) = 1 t(n) = 1 + t(n-1) = 1 + t(n-2) =. . . k + t(n-k) Choose k = n-1 t(n) = n-1 + t(1) = n-1 + 1 = O(n) Consider the following time complexity: t(0) = 1 t(n) = 1 + 2 t(n-1) = 1 + 2(1 + 2 t(n-2)) = 1 + 2 + 4 t(n-2) = 1 + 2 + 4(1 + 2 t(n-3)) = 1 + 2 + 4 + 8 t(n-3) = 1 + 2 +. . . + 2 k-1 + 2 kt(n-k) Choose k = n t(n) = 1 + 2 +. . . 2 n-1 + 2 n = 2 n+1 - 1 26

Binary Search • Given a sorted vector a[ ], find the location of element X unsigned int binary_search(vector<int> a, int X) { unsigned int low = 0, high = a. size()-1; while (low <= high) { int mid = (low + high) / 2; if (a[mid] < X) low = mid + 1; else if( a[mid] > X ) high = mid - 1; else return mid; } return NOT_FOUND; } • • Input size: n = a. size() Complexity = O( k iterations x (1 comparison+1 assignment) per loop) = O(log(n)) 27