Chapter 2 Access Control Matrix Overview Access Control

Chapter 2: Access Control Matrix • Overview • Access Control Matrix Model • Protection State Transitions – Commands – Conditional Commands Slide #2 -1

Overview • Protection state of system – The state of a system is the collection of the current values of all memory locations, secondary storage, registers, and other components of the system • Access control matrix – Describes protection state precisely – Matrix describing rights of subjects – State transitions change elements of matrix Slide #2 -2

Description objects (entities) subjects o 1 … om s 1 … sn s 1 s 2 … sn • Subjects S = { s 1, …, sn } • Objects O = { o 1, …, om } • Rights R = { r 1, …, rk } • Entries A[si, oj] R • A[si, oj] = { rx, …, ry } means subject si has rights rx, …, ry over object oj Slide #2 -3

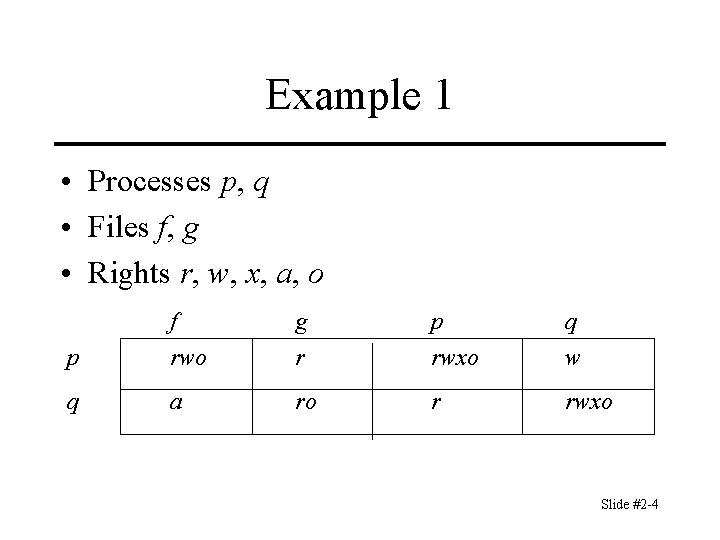
Example 1 • Processes p, q • Files f, g • Rights r, w, x, a, o f g p q p rwo r rwxo w q a ro r rwxo Slide #2 -4

Example 2 • Procedures inc_ctr, dec_ctr, manage • Variable counter • Rights +, –, call inc_ctr dec_ctr manage counter + inc_ctr dec_ctr manage – call Slide #2 -5

State Transitions • Change the protection state of system • |– represents transition – Xi |– Xi+1: command moves system from state Xi to Xi+1 – Xi |– * Xi+1: a sequence of commands moves system from state Xi to Xi+1 • Commands often called transformation procedures Slide #2 -6

Primitive Operations (HRU model) • create subject s; create object o – Creates new row, column in ACM; creates new column in ACM • destroy subject s; destroy object o – Deletes row, column from ACM; deletes column from ACM • enter r into A[s, o] – Adds r rights for subject s over object o • delete r from A[s, o] – Removes r rights from subject s over object o Slide #2 -7

Creating File • Process p creates file f with r and w permission command create • file(p, f) create object f; enter own into A[p, f]; enter r into A[p, f]; enter w into A[p, f]; end Slide #2 -8

Mono-Operational Commands • Make process p the owner of file g command make • owner(p, g) enter own into A[p, g]; end • Mono-operational command – Single primitive operation in this command Slide #2 -9

Conditional Commands • Let p give q r rights over f, if p owns f command grant • read • file • 1(p, f, q) if own in A[p, f] then enter r into A[q, f]; end • Mono-conditional command – Single condition in this command Slide #2 -10

Multiple Conditions • Let p give q w rights over f, if p owns f and p has c rights over q command grant • write • file • 2(p, f, q) if own in A[p, f] and c in A[p, q] then enter w into A[q, f]; end Slide #2 -11

Key Points • Access control matrix simplest abstraction mechanism for representing protection state • Transitions alter protection state • 6 primitive operations alter matrix – Transitions can be expressed as commands composed of these operations and, possibly, conditions Slide #2 -12

Postcript In our model a computer system is represented by a family of states: the set of all reachable states must be a subset of the set of secure states, if the system is to be secure. Slide # 2 -13

Security – Leaking rights Let R be the set of generic (primitive) rights of the system, r e R and let A be the ACM. Definitions 1. If r e R is added to an element of A not already containing r, then r is said to be leaked. 2. Let s 0 be the initial protection state. a. If a system can never leak the right r e R then the system is safe with respect to r. b. If a system can leak r e R then the system is called unsafe with respect to r. Slide # 2 -14

Safe vs secure We use the term safe to refer to the (abstract) model. Secure is used when referring to implementations. So a secure implementations must be modeled on a safe system. Slide # 2 -15

Foundation theorems The model we have discussed is called the Harrison-Ruzzo (HRU) model. Safety question Does there exist an algorithm for determining whether a given protection system (with initial state s 0) is safe with respect to a generic right r ? Slide # 2 -16

Theorem 1 There exists an algorithm that will determine whether a given mono-operational protection system with initial protection state s 0 is safe with respect to a generic right. Proof: A mono-operational command invokes a single primitive operation. Slide # 2 -17

Theorem 2 It is undecidable whether a given state of a given protection system is safe wrt a generic right. Proof –next Chapter. Slide # 2 -18