Chapter 2 8 Search Algorithms Search Algorithms Array




![Array Search TYPE Array. Of. Items = ARRAY[0. . n] OF Item; (* By Array Search TYPE Array. Of. Items = ARRAY[0. . n] OF Item; (* By](https://slidetodoc.com/presentation_image/fdb233e7bd282895000c107b7894711a/image-5.jpg)





















![Computation of the Next table i : = 1; k : = 0; Next[1] Computation of the Next table i : = 1; k : = 0; Next[1]](https://slidetodoc.com/presentation_image/fdb233e7bd282895000c107b7894711a/image-37.jpg)















- Slides: 58

Chapter 2. 8 Search Algorithms

Search Algorithms • Array Search – An array contains a certain number of records – Each record is identified by a certain key – One searches the record with a given key • String Search – A text is represented by an array of characters – One searches one or all occurrences of a certain string

Search Algorithms • Array Search – An array contains a certain number of records – Each record is identified by a certain key – One searches the record with a given key • String Search – A text is represented by an array of characters – One searches one or all occurrences of a certain string

Array Search PROCEDURE Search – Two parameters: • The Array to be searched – Contains n Items – Index in the range 0. . n – Item with index 0 is not used • The Key of the Item to be found – Search returns a Cardinal value • the index of the Item where the key has been found • if the key has not been found , 0.
![Array Search TYPE Array Of Items ARRAY0 n OF Item By Array Search TYPE Array. Of. Items = ARRAY[0. . n] OF Item; (* By](https://slidetodoc.com/presentation_image/fdb233e7bd282895000c107b7894711a/image-5.jpg)
Array Search TYPE Array. Of. Items = ARRAY[0. . n] OF Item; (* By convention, the element with index 0 is not used *) Item = RECORD Key : Key. Type (* any ordinal type *); Other record fields ; END;

Straight Search PROCEDURE Search ( VAR A: ARRAY OF Item, Key: Key. Type) : CARDINAL; VAR i : CARDINAL; BEGIN i : = HIGH(A); WHILE A[i]. Key # Key AND i # 0 DO DEC(i) END; RETURN i END Search;

Straight Search PROCEDURE Search ( VAR A: ARRAY OF Item, Key: Key. Type) : CARDINAL; VAR i : CARDINAL; BEGIN i : = HIGH(A); WHILE A[i]. Key # Key AND i # 0 DO DEC(i) END; RETURN i END Search;

Sentinel Search PROCEDURE Search ( VAR A: ARRAY OF Item, Key: Key. Type) : CARDINAL; VAR i : CARDINAL; BEGIN i : = HIGH(A); A[0]. Key : = Key; WHILE A[i]. Key # Key DO DEC(i) END; RETURN i END Search;

Binary Search # elements > 1 Yes No Key = Keyelement No Not Found Yes No Found Key < Keymiddle Binary Search right half Yes Binary Search left half # elements > 1

Binary Search (1) PROCEDURE Search(VAR a: ARRAY OF Item, Key: Key. Type): CARDINAL; VAR Min, Max, m: CARDINAL; PROCEDURE src(Min, Max: CARDINAL); … END src; BEGIN Min : = 1; Max : = HIGH(a); src(Min, Max); IF a[m]. Key = Key THEN RETURN m ELSE RETURN 0 END Search;

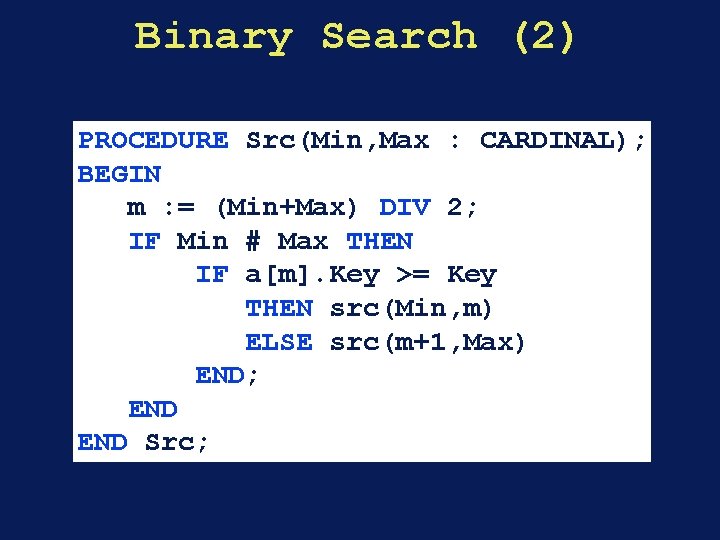
Binary Search (2) PROCEDURE Src(Min, Max : CARDINAL); BEGIN m : = (Min+Max) DIV 2; IF Min # Max THEN IF a[m]. Key >= Key THEN src(Min, m) ELSE src(m+1, Max) END; END Src;

Iterative Binary Search PROCEDURE Search(VAR a: ARRAY OF Item, Key: Key. Type): CARDINAL; VAR Min, Max, m: CARDINAL; BEGIN Min : = 1; Max : = HIGH(a); WHILE Min < Max DO m : = (Min+Max) DIV 2; IF a[m]. Key >= Key THEN Max : = m ELSE Min : = m+1 END; (* IF *) END; (* WHILE *) IF a[m]. Key = Key THEN RETURN m ELSE RETURN 0 END Search;

Array Search Performance (Number of comparisons) • Unordered Array – Straight search : 2 n – Sentinel search : n • Ordered Array – Binary search : log 2 n

Search Algorithms • Array Search – An array contains a certain number of records – Each record is identified by a certain key – One searches the record with a given key • String Search – A text is represented by an array of characters – One searches one or all occurrences of a certain string

String Search • The problem: Find a given string in a text. • Data structures: Text : ARRAY[1. . Text. Size] OF CHAR; String : ARRAY[1. . String. Size] OF CHAR; • The Algorithms: – Brute Force – Knuth, Morris & Pratt (KPM - 1974) – Boyer & Moore (BM - 1977)

String Search by Brute Force this algorithm tries to find a string WHILE current char. in Text # String[1] Move to next character in Text End of Text reached ? No WHILE char. in Text = char. in String Move to next character pair String matched OR Text exhausted

Brute Force String Search (Straightforward coding) PROCEDURE Search (VAR Text: Text. Type; TLength: CARDINAL; VAR String: String. Type; SLength: CARDINAL): CARDINAL; VAR j, jmax : CARDINAL; BEGIN j : = 0; jmax : = TLength - SLength; REPEAT WHILE (Text[j] # String[1]) AND (j <= jmax) DO j : = j+1 END; IF j <= jmax THEN i : = 2; WHILE (Text[j+i] = String[i]) AND (i < SLength) DO i : = i+1 END; (* IF *) j : = j + 1; UNTIL (i = SLength) OR (j > jmax); RETURN j - 1 END Search;

String Search (1) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in first position of string, Move string 1 position in text

String Search(2) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in fourth position of string, Move string 4 positions in text

String Search(3) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in fifth position of string, Move string 4 positions in text

String Search(4) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in first position of string, Move string 1 position in text

String Search(5) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in first position of string, Move string 1 position in text

String Search(6) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in second position of string, Move string 1 position in text

String Search(7) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT Mismatch in eight position of string, Move string 3 positions in text

String Search(8) by the KMP algorithm GATCAGCAATCATCATCACATC ATCATCACAT String found !

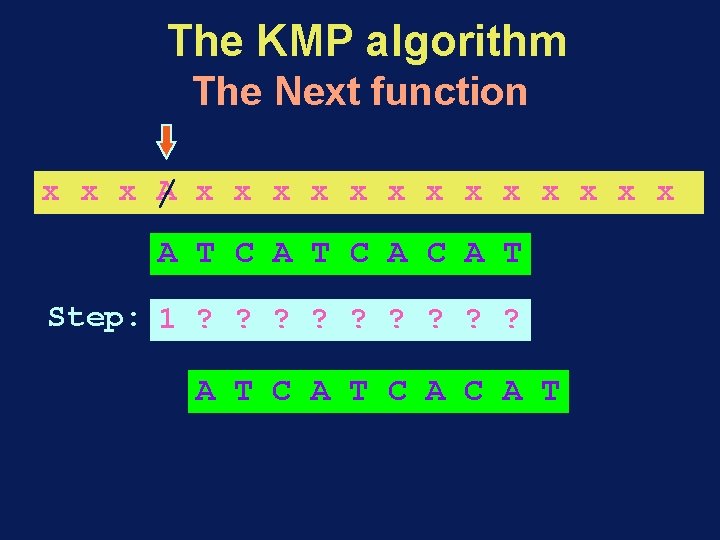
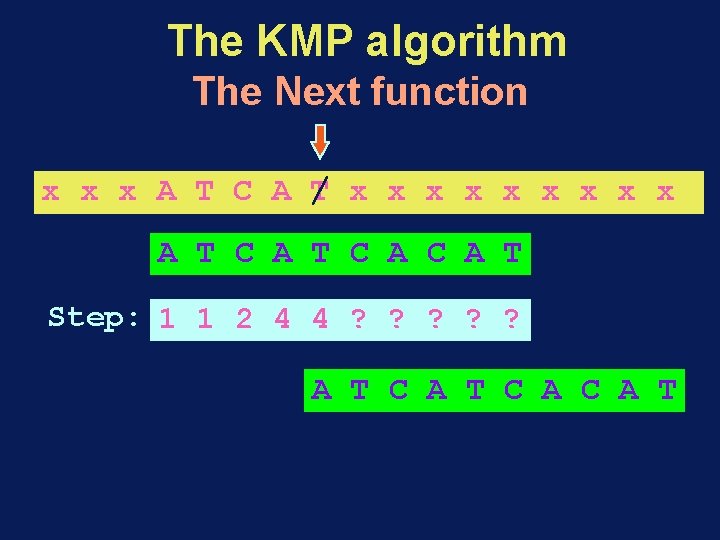
The KMP algorithm The Next function x x x / A x x x x A T C A C A T Step: 1 ? ? ? ? ? A T C A C A T

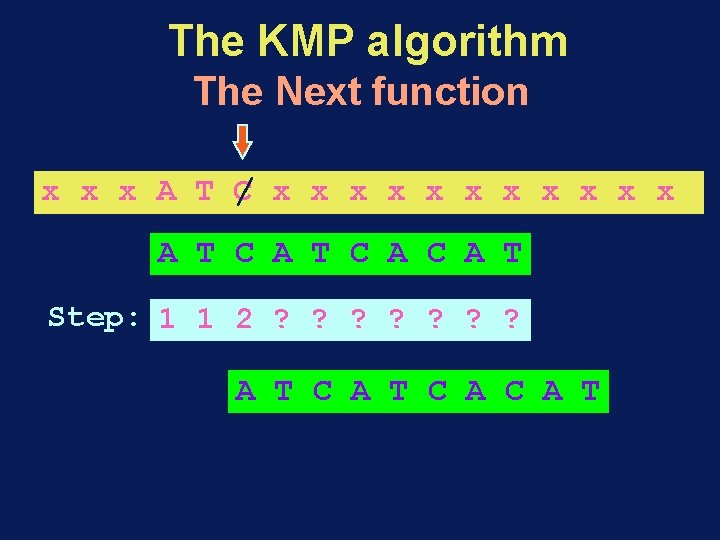
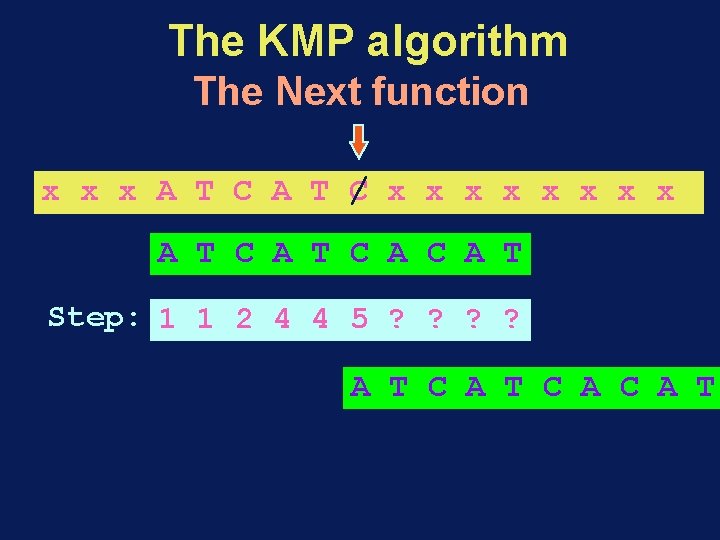
The KMP algorithm The Next function x x x A / T x x x A T C A C A T Step: 1 1 ? ? ? ? A T C A C A T

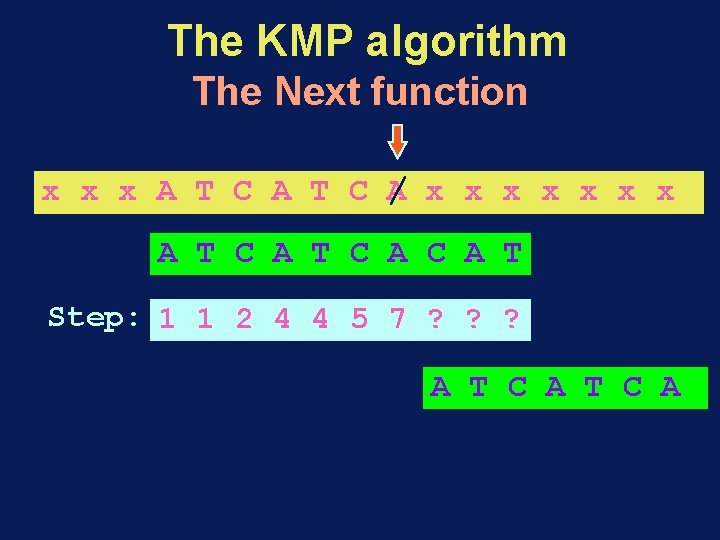
The KMP algorithm The Next function x x x A T C / x x x A T C A C A T Step: 1 1 2 ? ? ? ? A T C A C A T

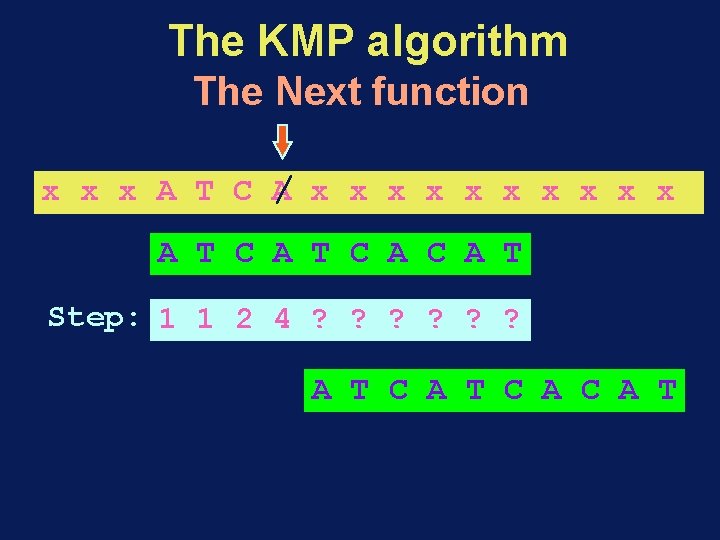
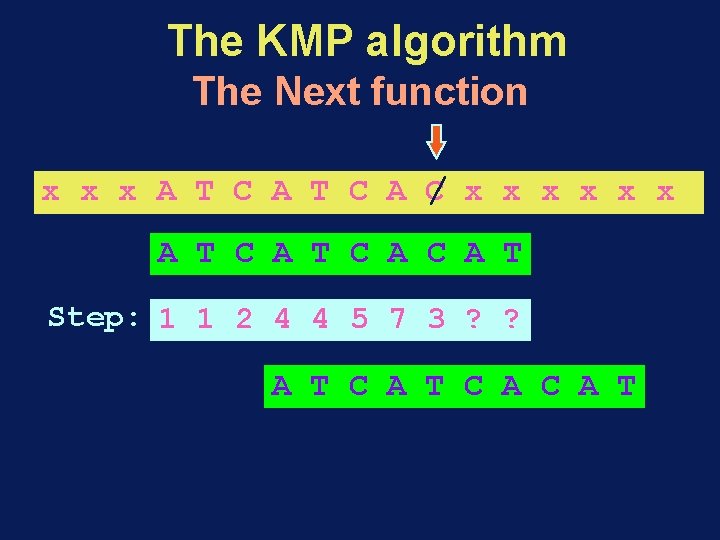
The KMP algorithm The Next function / x x x x A T C A T Step: 1 1 2 4 ? ? ? A T C A C A T

The KMP algorithm The Next function x x x A T C A / T x x x x x A T C A C A T Step: 1 1 2 4 4 ? ? ? A T C A C A T

The KMP algorithm The Next function x x x A T C A T / C x x x x A T C A C A T Step: 1 1 2 4 4 5 ? ? A T C A C A T

The KMP algorithm The Next function x x x A T C / A x x x x A T C A C A T Step: 1 1 2 4 4 5 7 ? ? ? A T C A

The KMP algorithm The Next function x x x A T C A C / x x x A T C A C A T Step: 1 1 2 4 4 5 7 3 ? ? A T C A C A T

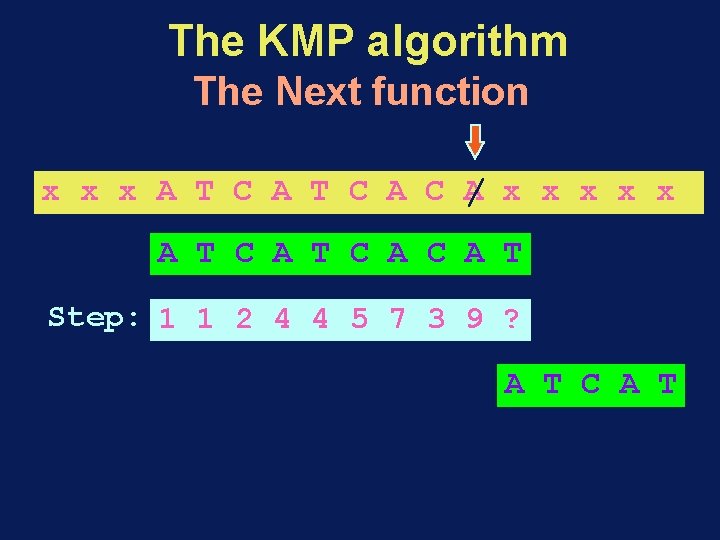
The KMP algorithm The Next function x x x A T C A C A / x x x A T C A C A T Step: 1 1 2 4 4 5 7 3 9 ? A T C A T

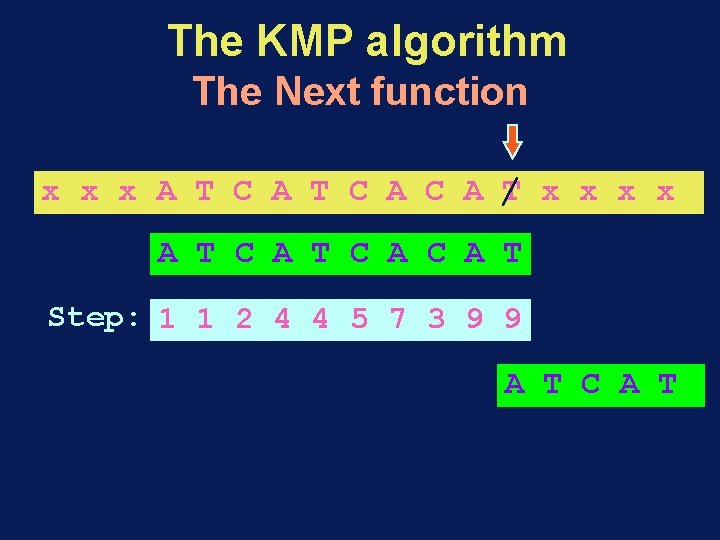
The KMP algorithm The Next function x x x A T C A C A / T x x A T C A C A T Step: 1 1 2 4 4 5 7 3 9 9 A T C A T

The KMP algorithm The Next function String: A T C A C A T 1 1 2 4 4 5 7 3 9 9 0 1 1 0 5 0 1 i = 1 2 3 4 5 6 7 8 9 10 Step: Next: Next[i] = i – Step[i]
![Computation of the Next table i 1 k 0 Next1 Computation of the Next table i : = 1; k : = 0; Next[1]](https://slidetodoc.com/presentation_image/fdb233e7bd282895000c107b7894711a/image-37.jpg)
Computation of the Next table i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *)

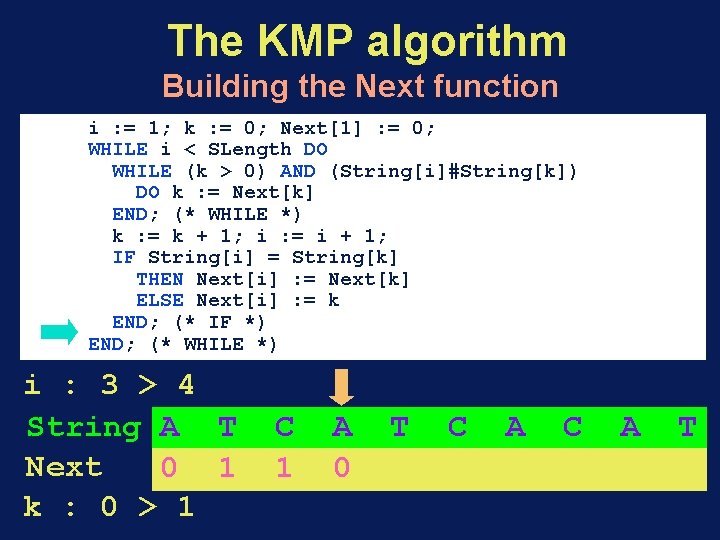
The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 1 String A Next 0 k : 0 T C A C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 1 String A Next 0 k : 0 T C A C A T

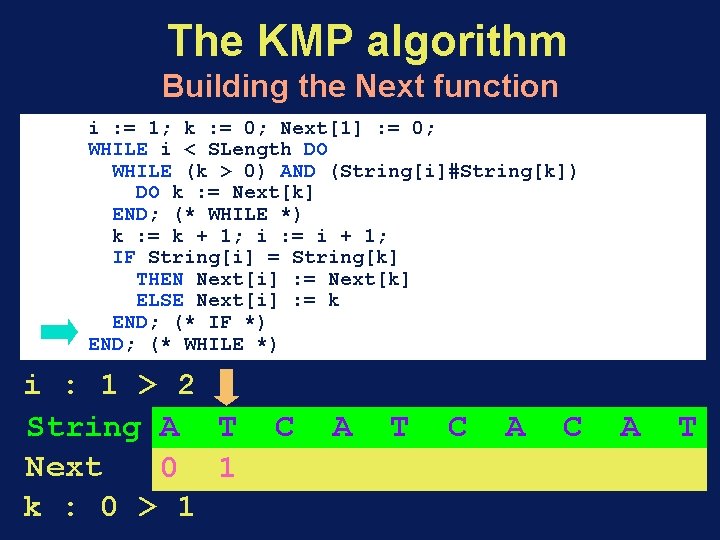
The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 1 > 2 String A T Next 0 1 k : 0 > 1 C A T

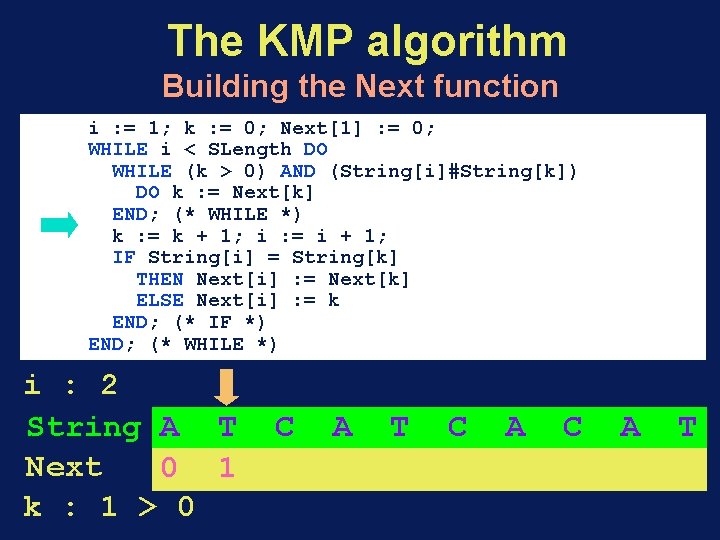
The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 2 String A T Next 0 1 k : 1 > 0 C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 2 > 3 String A T Next 0 1 k : 0 > 1 C 1 A T C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 3 String A T Next 0 1 k : 1 > 0 C 1 A T C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 3 > 4 String A T Next 0 1 k : 0 > 1 C 1 A 0 T C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 4 String A Next 0 k : 1 T 1 C 1 A 0 T C A T

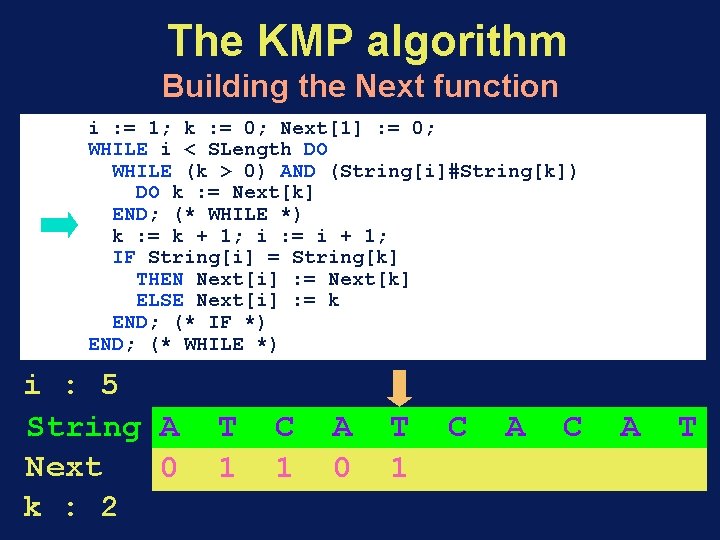
The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 4 > 5 String A T Next 0 1 k : 1 > 2 C 1 A 0 T C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 5 String A Next 0 k : 2 T 1 C 1 A 0 T 1 C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 5 > 6 String A T Next 0 1 k : 2 > 3 C 1 A 0 T 1 C 1 A C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 6 String A Next 0 k : 3 T 1 C 1 A 0 T 1 C 1 A C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 6 > 7 String A T Next 0 1 k : 3 > 4 C 1 A 0 T 1 C 1 A 0 C A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 7 String A Next 0 k : 4 T 1 C 1 A 0 C A T

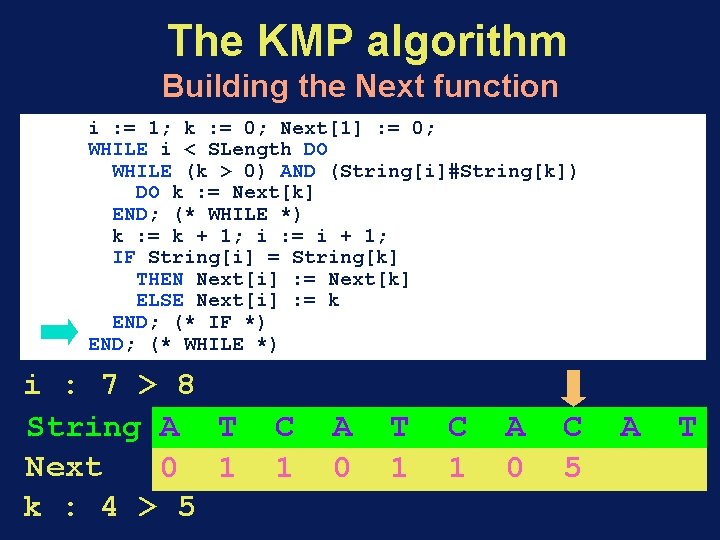
The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 7 > 8 String A T Next 0 1 k : 4 > 5 C 1 A 0 T 1 C 1 A 0 C 5 A T

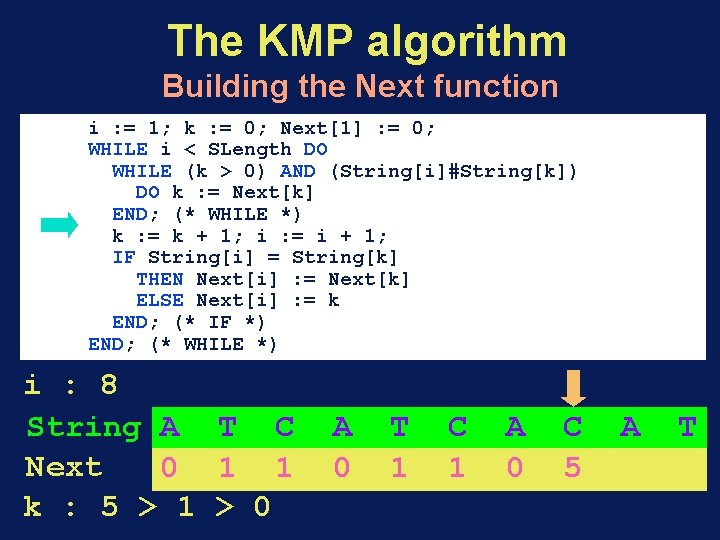
The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 8 String A T C Next 0 1 1 k : 5 > 1 > 0 A 0 T 1 C 1 A 0 C 5 A T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 8 > 9 String A T Next 0 1 k : 0 > 1 C 1 A 0 T 1 C 1 A 0 C 5 A 0 T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 9 String A Next 0 k : 1 T 1 C 1 A 0 C 5 A 0 T

The KMP algorithm Building the Next function i : = 1; k : = 0; Next[1] : = 0; WHILE i < SLength DO WHILE (k > 0) AND (String[i]#String[k]) DO k : = Next[k] END; (* WHILE *) k : = k + 1; i : = i + 1; IF String[i] = String[k] THEN Next[i] : = Next[k] ELSE Next[i] : = k END; (* IF *) END; (* WHILE *) i : 9 > 10 String A T Next 0 1 k : 1 > 2 C 1 A 0 T 1 C 1 A 0 C 5 A 0 T 1

Actual KMP search j : = 1; i : = 1; WHILE (i <= SLength) AND (j <= TLength) DO WHILE (i > 0) AND (Text[j] # String[i]) DO i : = Next[i] END; (* WHILE *) i : = i + 1; j : = j + 1; END; (* WHILE *) IF i > SLength THEN RETURN j - SLength ELSE RETURN TLength END; (* IF *)

String Search Performance • Text length = n characters • String length = m characters • The Algorithms: – Brute Force • Worst case search time : O(n*m) – Knuth, Morris & Pratt (KMP - 1974) • Worst case search time : O(n+m) – Boyer & Moore (BM - 1977) • Similar to but slightly better than KMP.