Chapter 2 4 Modula 2 Simple Types Constants

Chapter 2. 4 Modula 2 Simple Types

Constants and Variables • Constants – Name – Value The value of a constant belongs to a type. • Variables – Name – Type = set of all values the variable can have The type determines the internal representation of data as well as the operations that can be performed on the data

Types in Modula 2 • Simple Types: values can’t be decomposed – Ordinal Types: bijection with natural numbers – Reals: approx. representation for real values – Pointers: addresses in data memory • Structured Types: Values have # components – Arrays: all components have same type – Records: components can have # types – Sets: small sets of ordinal values – Procedures: entire subprograms

Simple Types • Ordinal Types – Enumerated types – BOOLEAN type – CHAR type – CARDINAL type – INTEGER type – Subrange types • REAL Type • POINTER Type

Enumerated Types • Possible values: User defined TYPE Day = (Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday) • Operators : Only relational (= , # , > , < , >= , <=) – Ordering by enumeration Day = (Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday); Monday < Sunday Day = (Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday); Monday > Sunday

Enumerated Types • Main benefit : Clarity TYPE Sex = (Male, Female); VAR Sex. A, Sex. B : Sex; . . . IF Sex. A = Male THEN Sex. B : = Female ELSE Sex. B : = Male END (* IF *) • Replaces manual encoding (* Male encoded by 0, Female by 1 *) VAR Sex. A, Sex. B : CARDINAL; . . . Sex. B : = 1 - Sex. A;

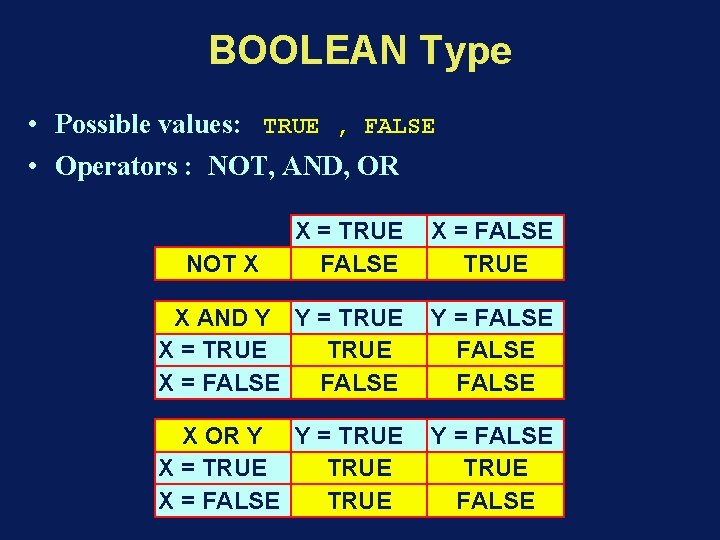
BOOLEAN Type • Possible values: TRUE , FALSE • Operators : NOT, AND, OR X = TRUE FALSE X = FALSE TRUE X AND Y Y = TRUE X = FALSE Y = FALSE X OR Y Y = TRUE X = FALSE TRUE Y = FALSE TRUE FALSE NOT X

Relational Expressions have a BOOLEAN value • • a=b a#b a>b a<b a >= b a <= b a IN b TRUE when a equals b TRUE when a different from b TRUE when a greater than b TRUE when a less than b TRUE when a greater or equal b TRUE when a less or equal b TRUE when value of a belongs to the set b

CHAR Type • Possible values: all characters of a system specific alphabet. • In many systems : extended ASCII – 128 standardized characters + 128 additional characters – Various extensions for allowing non-anglosaxon characters • In new Microsoft & Java systems : UNICODE – 65536 different characters, adequate for all languages in the world. ASCII is a subset of UNICODE. • Operators : Only the relational operators – Order can be different in different alphabets. • Relative position of space, letters and digits VAN ZOERSEL Van Zoersel VANANTWERPEN van Gorp

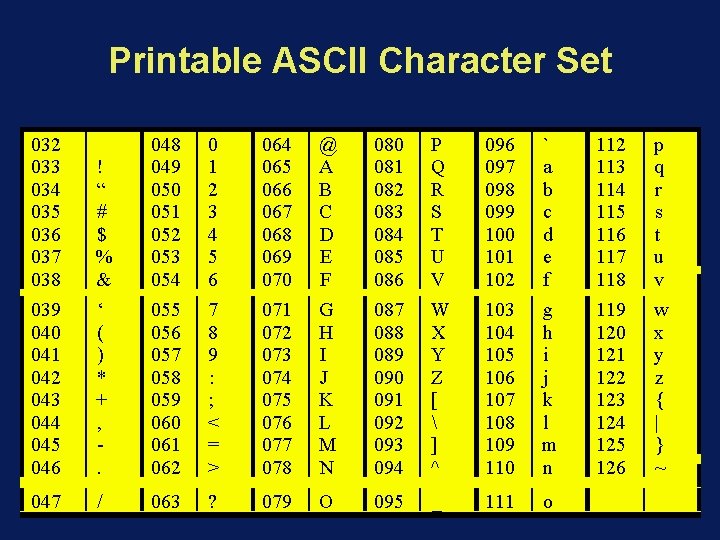
Printable ASCII Character Set 032 033 034 035 036 037 038 ! “ # $ % & 048 049 050 051 052 053 054 0 1 2 3 4 5 6 064 065 066 067 068 069 070 @ A B C D E F 080 081 082 083 084 085 086 P Q R S T U V 096 097 098 099 100 101 102 ` a b c d e f 112 113 114 115 116 117 118 p q r s t u v 039 040 041 042 043 044 045 046 ‘ ( ) * + , . 055 056 057 058 059 060 061 062 7 8 9 : ; < = > 071 072 073 074 075 076 077 078 G H I J K L M N 087 088 089 090 091 092 093 094 W X Y Z [ ] ^ 103 104 105 106 107 108 109 110 g h i j k l m n 119 120 121 122 123 124 125 126 w x y z { | } ~ 047 / 063 ? 079 O 095 _ 111 o

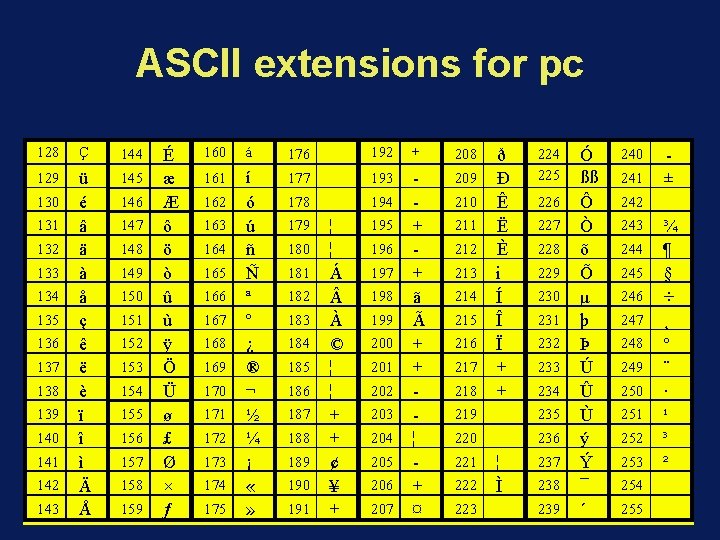
ASCII extensions for pc 128 Ç 144 129 ü é â ä à å ç ê ë è ï î ì Ä Å 145 130 131 132 133 134 135 136 137 138 139 140 141 142 143 146 147 148 149 150 151 152 153 154 155 156 157 158 159 É æ Æ ô ö ò û ù ÿ Ö Ü ø £ Ø × ƒ 160 á 176 161 í ó ú ñ Ñ ª º ¿ ® ¬ ½ ¼ ¡ « » 177 162 163 164 165 166 167 168 169 170 171 172 173 174 175 178 179 180 181 182 183 184 185 186 187 188 189 190 191 _ _ _ ¦ ¦ Á À © ¦ ¦ + + ¢ ¥ + 192 + 208 193 + + ã Ã + + ¦ + ¤ 209 194 195 196 197 198 199 200 201 202 203 204 205 206 207 210 211 212 213 214 215 216 217 218 219 220 221 222 223 ð Ð Ê Ë È i Í Î Ï + + _ _ ¦ Ì _ 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 Ó ßß Ô Ò õ Õ µ þ Þ Ú Û Ù ý Ý ¯ ´ 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 ± _ ¾ ¶ § ÷ ¸ ° ¨ · ¹ ³ ² _

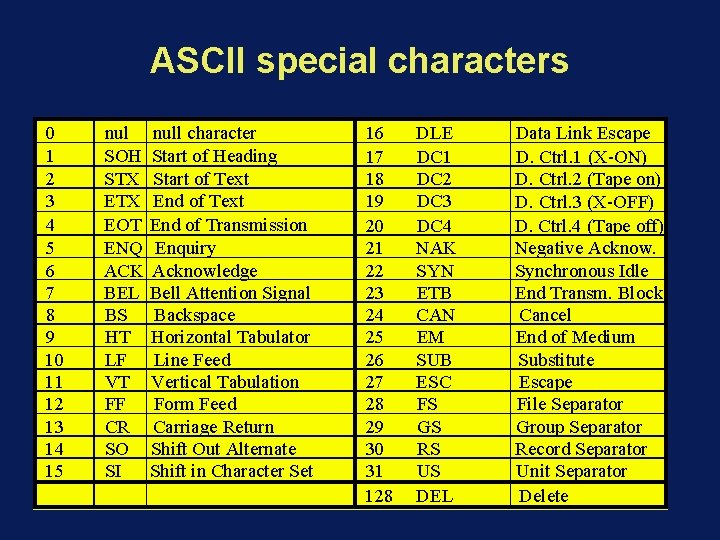
ASCII special characters 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 nul SOH STX EOT ENQ ACK BEL BS HT LF VT FF CR SO SI null character Start of Heading Start of Text End of Transmission Enquiry Acknowledge Bell Attention Signal Backspace Horizontal Tabulator Line Feed Vertical Tabulation Form Feed Carriage Return Shift Out Alternate Shift in Character Set 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 128 DLE DC 1 DC 2 DC 3 DC 4 NAK SYN ETB CAN EM SUB ESC FS GS RS US DEL Data Link Escape D. Ctrl. 1 (X ON) D. Ctrl. 2 (Tape on) D. Ctrl. 3 (X OFF) D. Ctrl. 4 (Tape off) Negative Acknow. Synchronous Idle End Transm. Block Cancel End of Medium Substitute Escape File Separator Group Separator Record Separator Unit Separator Delete

CARDINAL Type • Possible values: implementation dependant – With 16 bit representations : 0 <= C < 216 = 65536 – With 32 bit representations : 0 <= C < 232 ~ 4. 10 9 • Operators : relational + + * DIV MOD addition subtraction multiplication integer quotient integer remainder • Examples : 5 DIV 2 = 2 5 MOD 2 = 1 5 DIV 7 = 0 5 MOD 7 = 5 5 DIV 1 = 5 5 MOD 1 = 0

INTEGER Type • Possible values: implementation dependant – With 16 bit representations : -215 <= I < 215 = 32768 – With 32 bit representations : -231 <= I < 231 ~ 2. 10 9 • Operators : relational + + * DIV MOD addition subtraction multiplication integer quotient integer remainder • Examples : 5 DIV 2 = 2 5 MOD 2 = 1 -5 DIV 2 = -2 -5 MOD 2 = ? ? 5 DIV -2 = -2 5 MOD -2 = ? ?

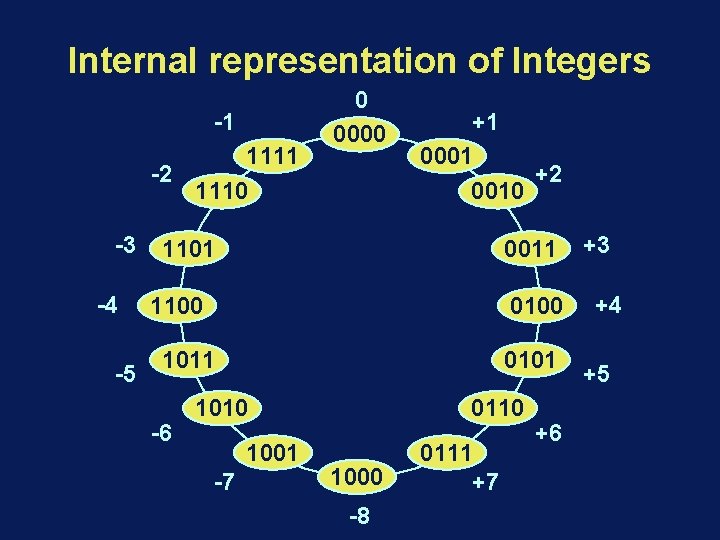
Internal representation of Integers • Conventions: n M M' = number of bits in representation = value to be represented = value of representation • Two's complement definition: M' = (M + 2 n) MOD 2 n • Range: 2 n 1 <= I < 2 n 1

Internal representation of Integers -1 1111 -2 1110 -3 -4 -5 0 0000 +1 0001 +2 0010 1101 0011 1100 0100 1011 -6 0101 1010 1001 -7 0110 1000 -8 0111 +7 +6 +3 +4 +5

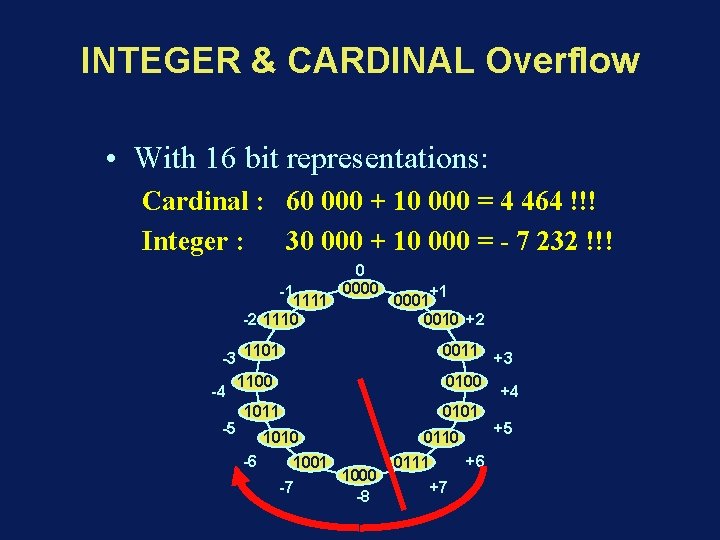
INTEGER & CARDINAL Overflow • With 16 bit representations: Cardinal : 60 000 + 10 000 = 4 464 !!! Integer : 30 000 + 10 000 = - 7 232 !!! -1 1111 -2 1110 -3 1101 1100 -4 1011 -5 1010 -6 1001 -7 0 0000 1000 -8 +1 0001 0010 +2 0011 +3 0100 +4 0101 +5 0110 +6 0111 +7

Score: -32276 With thanks to Ariane for the score

Subrange Types • For all ordinal types subrange types can be defined TYPE Day Week. Day. Of. Month = = (Mon, Tue, Wed, Thu, Fri, Sat, Sun); [Mon. . Fri]; [1. . 31]; [1. . 12]; • Why Subranges ? – Makes out-of-range detection possible – Allows optimized memory allocation by compiler

Functions and Operators for ordinal types • The ORD function returns the internal representation of any ordinal variable as a cardinal value. TYPE VAR Day = (Mon, Tue, Wed, Thu, Fri, Sat, Sun); X : Day; Ch : CHAR; . . . X : = Wed; Ch : = "A"; (* ORD(X) = 2 *) (* ORD(Ch) = 65 *)

Functions and Operators for ordinal types • The CHR function returns the character represented internally by a given cardinal value. VAR Ch n : CHAR; : [0. . 9]; . . . n : = 3; (* Conversion of a cardinal value between 0 and 9 into the corresponding character *) Ch : = CHR(ORD("0")+n);

Functions and Operators for ordinal types • The VAL function returns the value in a specified type represented internally by a given cardinal value. TYPE VAR Day = (Mon, Tue, Wed, Thu, Fri, Sat, Sun); Ch : CHAR; Today : Day; . . . Today : = VAL(Day, 2); (* Wednesday *) Ch : = VAL(CHAR, 65); (* "A" *) (* VAL(CHAR, n) = CHR(n) *)

Functions and Operators for ordinal types • The INC and DEC procedures can be used to increment or decrement ordinal variables. TYPE VAR Day = (Mon, Tue, Wed, Thu, Fri, Sat, Sun); Ch : CHAR; Today : Day; . . . Today: =Wed ; INC(Today); (* Today = Thu *) Ch : = "A"; INC(ch, 32); (* ch = "a" *)

REAL Type Approximate representation for real numbers • Possible values and accuracy: – implementation dependant – majority of computer systems : IEEE 754. • Single precision (32 bit) "REAL" – Smallest value – Largest value – Relative error : 1. 18 10 -38 : 3. 39 10+38 : < 3. 0 10 -8 • Double precision (64 bit) "LONGREAL" – Smallest value – Largest value – Relative error : 1. 18 10 -308 : 3. 39 10+308 : < 1. 1 10 -16

REAL Type Operators and type conversions • • Arithmetic operators : +, -, *, / Relational operators : =, #, >, >=, <, <= Expressions : No mixing of types Type conversions: – From REAL to INTEGER : Truncation ! Int. Var : = VAL(INTEGER, Real. Val); Int. Var : = TRUNC(Real. Val); – From INTEGER to REAL : Real. Val : = VAL(REAL, Int. Val); Real. Val : = FLOAT(Int. Val);

REAL Type Example CONST BEFper. EURO = 40. 3399; VAR EUROValue : REAL; BEFValue : CARDINAL; Real. Bef : REAL; . . . Real. BEF : = EUROValue * BEFper. EURO; BEFValue : = VAL(CARDINAL, Real. BEF+0. 5)

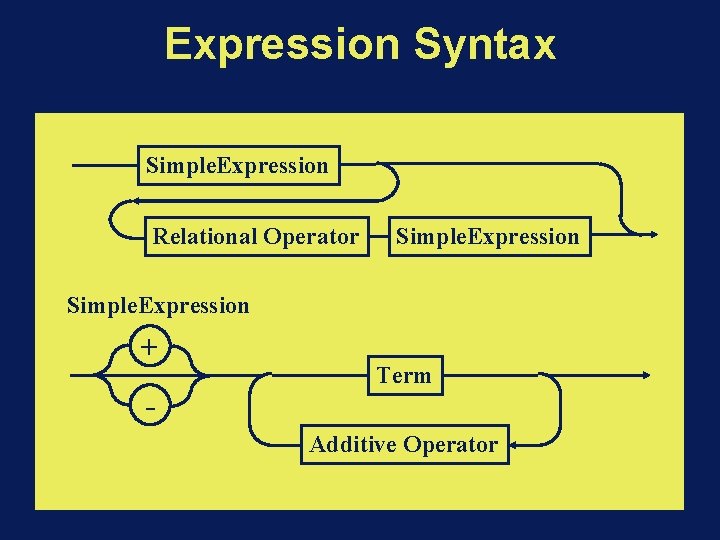
Expression Syntax Simple. Expression Relational Operator Simple. Expression + - Term Additive Operator

Term Syntax Factor Multiplicative Operator

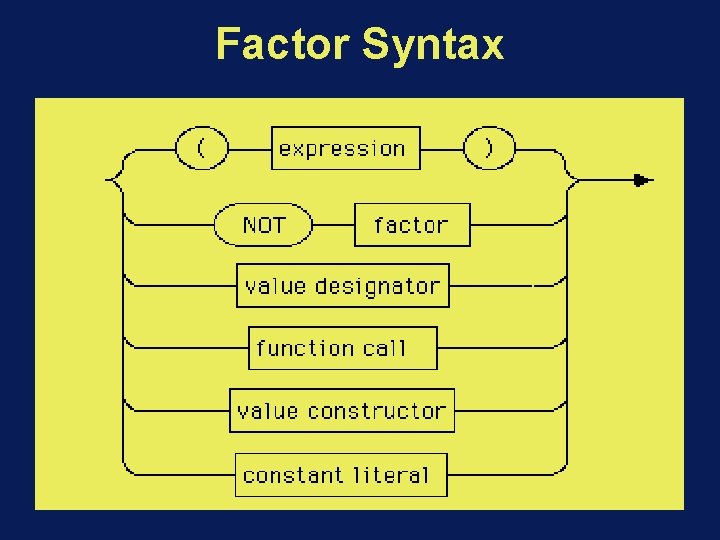
Factor Syntax

Expression Evaluation • Order of evaluation: 1 Factor 2 Term 3 Simple Expression 4 Expression • Parentheses can modify order • Evaluation is done from left to right, in a lazy fashion