Chapter 2 2 STANDARD NORMAL DISTRIBUTIONS Normal Distributions

Chapter 2. 2 STANDARD NORMAL DISTRIBUTIONS

Normal Distributions • Last class we looked at a particular type of density curve called a Normal distribution. • All Normal distributions are described by two μ σ parameters: ____ and _____ • Because of this, we can abbreviate a Normal distribution as ____(___, N μ ___) σ • Another important quality of Normal distributions is that the follow the _____ Empirical rule. This rule states 68 of the data falls within 1 standard deviation that ____% of the mean, ____% falls within 2 standard deviations 95 99. 7 falls within 3 standard deviations. and _____%

The Standard Normal Distribution • All normal distributions are the same if we measure in units of size σ about the mean μ as center. • Changing these units requires that we standardize (like we did in 2. 1) Z=x-μ σ • If the variable we standardize has a normal distribution, then so does the new variable, z • The new distribution is called the standard Normal Distribution

*The standard Normal distribution follows a normal distribution and has mean 0 and standard deviation 1 *Notice that the distribution is perfectly symmetric about 0.

Great…but why is that useful? • Remember, the area under a density curve is a proportion of the observations in a distribution. 1 – The area under the entire density curve is ____. – The proportion of observations to the left of the. 5 median is_____. • We can find the proportion of observation that lie within any range of values simply by finding the area under the curve.

The standard Normal Table • Because standardizing Normal distributions makes them all the same, we can use a single table to find the areas under a Normal distribution. • This table is called the standard Normal table. – It’s inside the front cover of you textbook! – You will be given this table on the AP exam

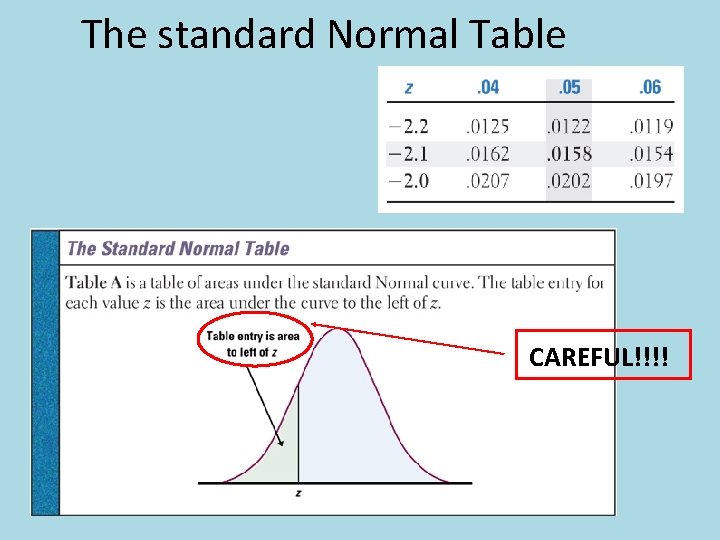
The standard Normal Table CAREFUL!!!!

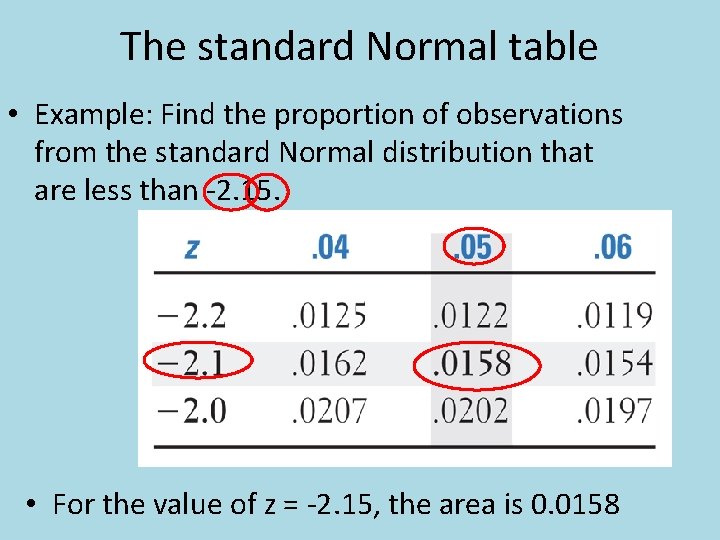
The standard Normal table • Example: Find the proportion of observations from the standard Normal distribution that are less than -2. 15. • For the value of z = -2. 15, the area is 0. 0158

Using the standard Normal table… • Caution: the area that we found was to the LEFT of z = 2. 15. In this case, that is what we were looking for. • HOWEVER if the problem had asked for the area lying to the right of -2. 15. What would that answer be?

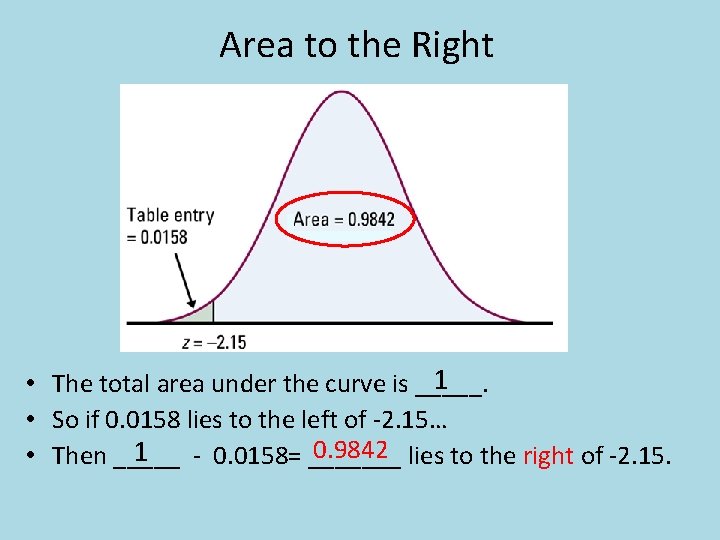
Area to the Right 1 • The total area under the curve is _____. • So if 0. 0158 lies to the left of -2. 15… 0. 9842 lies to the right of -2. 15. 1 - 0. 0158= _______ • Then _____

How do you avoid making a mistake when asked to find the area to the RIGHT? • Always sketch the Normal curve, mark the zvalue, and shade the area of interest (aka the area you are looking for in the problem) • THEN, when you get you answer, CHECK TO SEE IF IT IS REASONABLE!!!

Putting it all Together: Solving Problems Involving Normal Distributions • Step 1: State the problem in terms of the observed variable x. Draw a picture of the distribution and shade the area of interest. – Hint…use σ and μ • Step 2: Standardize and draw a picture. We need to standardize x to restate the problem in terms of a standard Normal variable z. Draw a new picture to show the area of interest under our now standard Normal curve.

Putting it all Together: Solving Problems Involving Normal Distributions • Step 3: Use the table. Find the are under the standard Normal curve using Table A. (careful if the problem asks for the area to the right) • Step 4: Conclusion. Write your conclusion in the context of the problem. – Just saying “the area under the curve that is less that 2. 1” means nothing! Your results should tell you something about the data.

Example: Cholesterol and Young Boys • For 14 -year-old boys, the mean is μ = 170 milligrams of cholesterol per deciliter of blood (mg/dl) and the standard deviation σ = 30 mg/dl. • Levels above 240 mg/dl may require medical attention. What percent of 14 -year-old boys have more than 240 mg/dl of cholesterol?

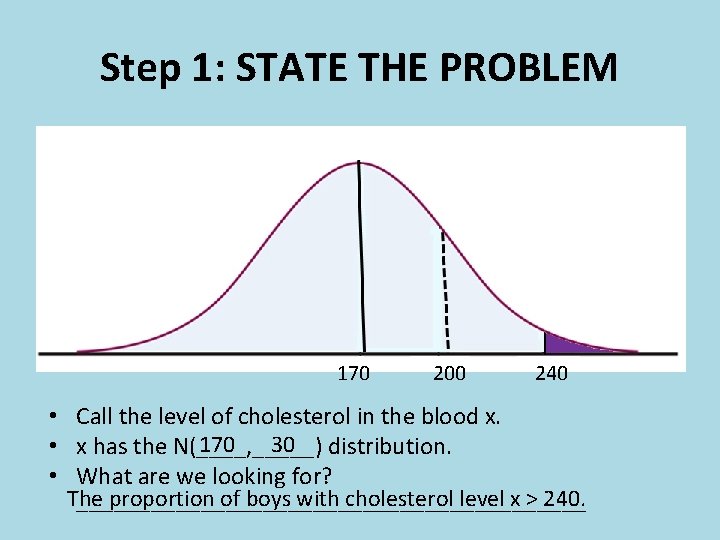
Step 1: STATE THE PROBLEM 170 200 240 • Call the level of cholesterol in the blood x. 170 30 distribution. • x has the N(____, _____) • What are we looking for? The proportion of boys with cholesterol level x > 240. _____________________

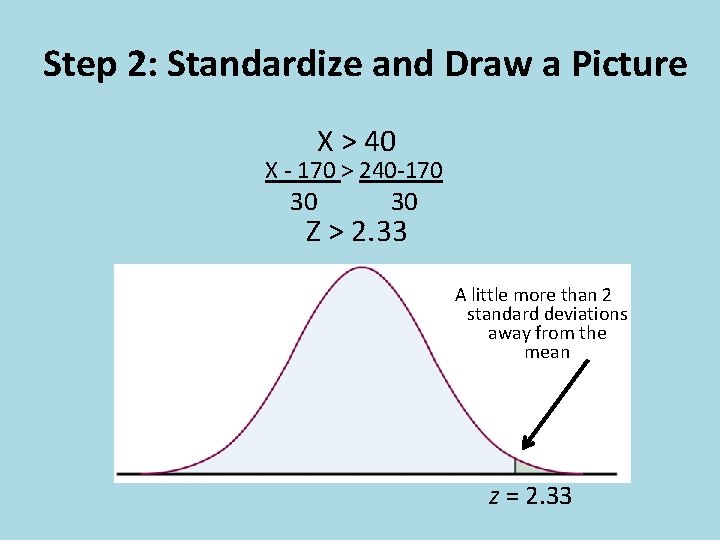
Step 2: Standardize and Draw a Picture X > 40 X - 170 > 240 -170 30 30 Z > 2. 33 A little more than 2 standard deviations away from the mean z = 2. 33

Step 3: Use the Table Use Table A to look up z = 2. 33 *look for 2. 3 on the left and then move over until you are under 0. 03*

Step 4: Conculsion • Don’t forget to state your conclusion in the context of the question! • Remember, we were trying to find out how many 14 -year-old boys have cholesterol levels over 240 mg/dl because boys over this level require medical attention. • So what does our conclusion mean? Only about 1% of 14 -year-old boys have cholesterol levels that require medical attention.

Finding a Value when Given a Proportion • What if you wanted to know what score you would have to get in order to place among the top 10% of your class on a test? • Sometimes, we may be asked to find the observed value with a given proportion of the observations above or below it. • To do this, we just read Table A going backwards. In other words, find the proportion you are looking for in the body of the table, figure out the corresponding zscore, and then “unstandardize” to get the observed value.

Inverse Normal Calculation Example • Scores on the SAT Verbal test in recent years follow approximately the N(505, 110) distribution. How high must a student score in order to place in the top 10% of all students taking the SAT. Step 1: State the problem and draw a picture • We are looking for the SAT score x with an. 10 to its _____ right under the Normal area of ____ 505 and standard curve with a mean μ =______ 110 deviation σ = _____.

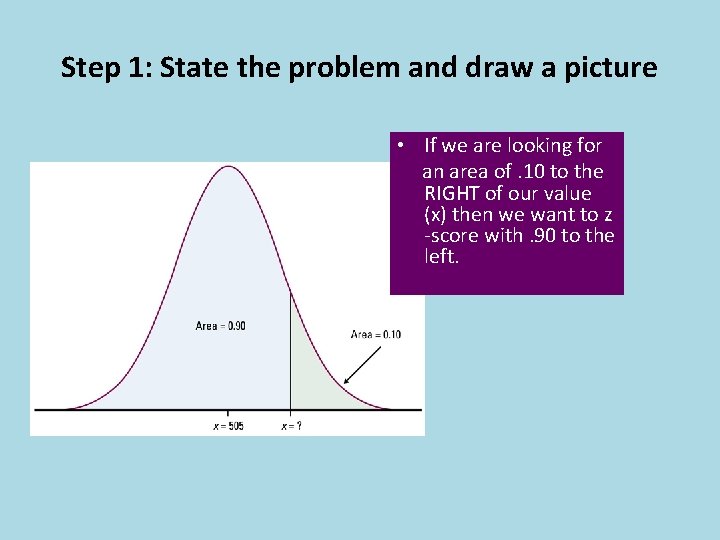
Step 1: State the problem and draw a picture • If we are looking for an area of. 10 to the RIGHT of our value (x) then we want to z -score with. 90 to the left.

Step 2: Use the Table • Look at the body of Table A (remember, we KNOW the proportion—. 90—we are LOOKING for the z-score. . 8997 • The entry closest to. 9 is _______. This entry 1. 28 corresponds with z=_____. • So our unknown x has a standardized value of 1. 28 _______.

Step 3: Unstandardize • We have the standardized value for x, but we need to unstandardized value in order to answer our question. X - 505 = 128 110 x = 645. 8

Step 4: Conclusion • Put the results into the context of the question…what would you say knowing that x = 645. 8? • Scores on the SAT Verbal test in recent years follow approximately the N(505, 110) distribution. How high must a student score in order to place in the top 10% of all students taking the SAT.

Next time on Statistics AP • The Chapter 2 Test will be on WEDNESDAY! – It will cover all of Chapter 2 • SO on Monday we will – Learn about Normal Probability Plots – Learn how to do standard Normal calculations using our calculators (yay!) and talk about avoiding “calculator speak” on the AP – Review Chapter 2 • YOUR HOMEWORK: – Exercises 2. 29, 2. 30 (ignore Normal Curve Applet part), 2. 31 - 2. 34

Assessing Normality • The normal distribution provides a good model for come distributions of real data. • However, not all distributions are Normal. • It is important to assess the Normality of distributions before we assume that they are normal. • This will be very important when we learn about statistical inference procedures (much later)

Assessing Normality Method 1 • One method for assessing normality is to construct a histogram or a stemplot and then see if the graph is approximately bell-shaped and symmetric about the mean. • Histograms and stemplots can reveal important “non-Normal” features of a distributions such as skewness, outliers, or gaps and clusters.

Method 1 Continued • For example, this distribution of vocabulary scores appears Normal. – The distribution is bell-shaped, it is roughly symmetric, there are no gaps or clusters, and there do not appear to be any outliers.

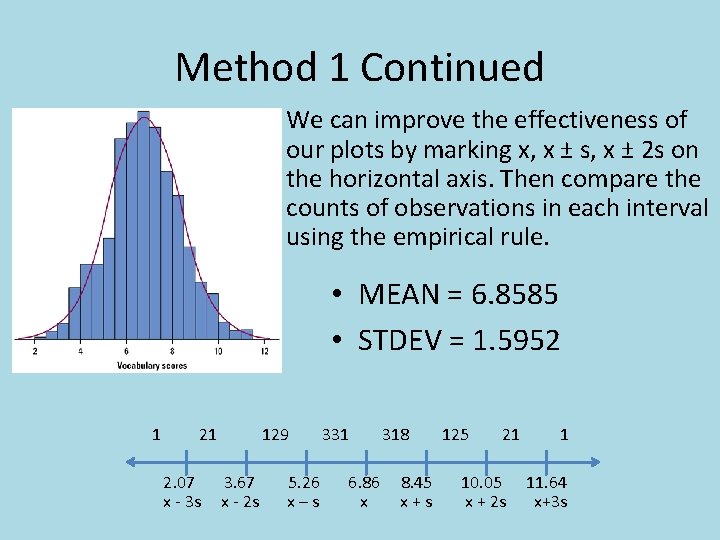
Method 1 Continued • the We can improve the effectiveness of our plots by marking x, x ± s, x ± 2 s on the horizontal axis. Then compare the counts of observations in each interval using the empirical rule. • MEAN = 6. 8585 • STDEV = 1. 5952 1 21 2. 07 x - 3 s 129 3. 67 x - 2 s 5. 26 x–s 331 6. 86 x 318 8. 45 x+s 125 21 10. 05 x + 2 s 1 11. 64 x+3 s

Method 1 Continued 1 21 2. 07 x - 3 s 129 3. 67 x - 2 s 5. 26 x–s 331 6. 86 x 318 8. 45 x+s 125 21 10. 05 x + 2 s 1 11. 64 x+3 s • Does the distribution follow the empirical rule? • There a total of 947 observations • What percent fall within 1 standard deviation of the 68. 5% mean? _____ • How does this compare with the empirical rule? 95. 4% • What percent fall within 2 standard deviations? _____ • How does this compare with the empirical rule? 99. 8% • Within 3 standard deviations? ______ • How does this compare with the empirical rule?

Method 1 Continued… • Because the actual counts of our distribution follow the empirical rule very closely, we can confirm that the Normal distribution with μ = 6. 86 and σ = 1. 595 fits the data well.

Method #2 for Assessing Normality • Construct a normal probability plot. This requires the use of your graphing calculator. • Basically…without a calculator. . – Arrange the observed data values from smallest to largest. Record what percentile of the data set each value occupies. (i. e. , the smallest observation in a set of 20 is the 5% point, the second smallest is the 10%, etc) – Use the standard Normal distribution table to find the z-scores for these percentiles. (i. e. , z = -1. 645 is the 5% point of the standard Normal distribution) – Plot each data point x against the corresponding z.

Method 2 Continued • Let’s interpret some Normal probability plots!

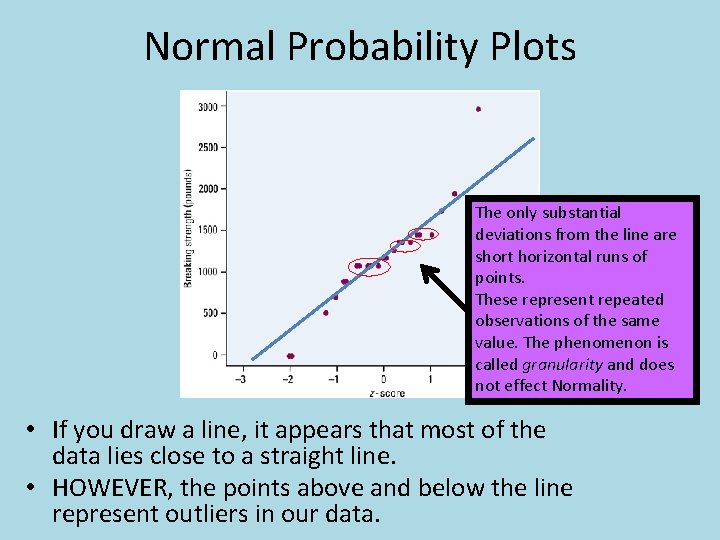
Normal Probability Plots The only substantial deviations from the line are short horizontal runs of points. These represent repeated observations of the same value. The phenomenon is called granularity and does not effect Normality. • If you draw a line, it appears that most of the data lies close to a straight line. • HOWEVER, the points above and below the line represent outliers in our data.

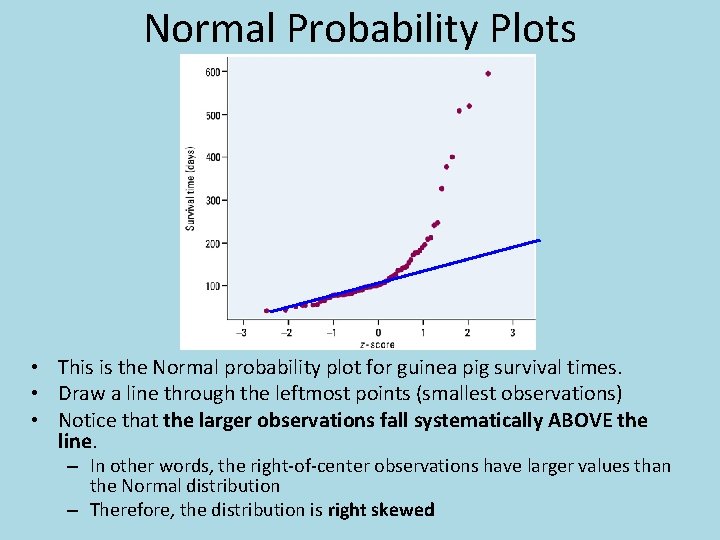
Normal Probability Plots • This is the Normal probability plot for guinea pig survival times. • Draw a line through the leftmost points (smallest observations) • Notice that the larger observations fall systematically ABOVE the line. – In other words, the right-of-center observations have larger values than the Normal distribution – Therefore, the distribution is right skewed

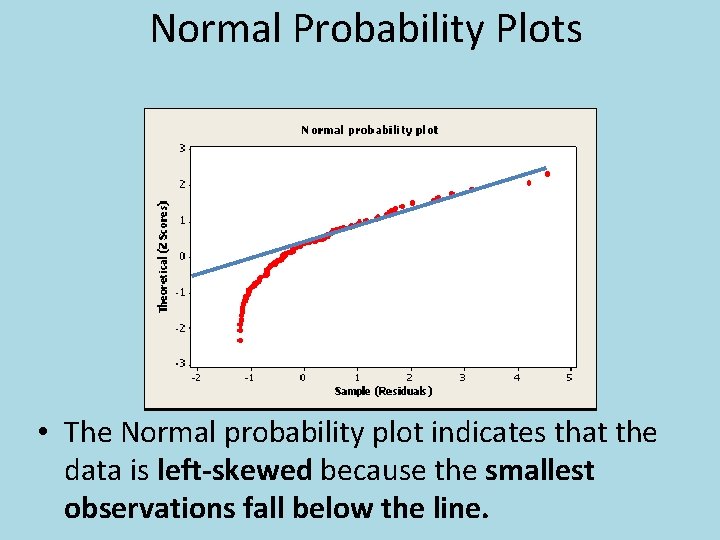
Normal Probability Plots • The Normal probability plot indicates that the data is left-skewed because the smallest observations fall below the line.

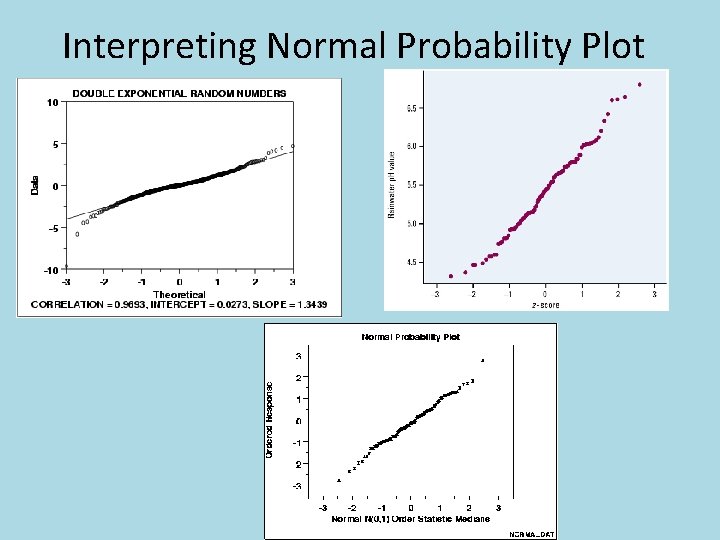
Interpreting Normal Probability Plot

Graphing Normal Probability Plots on your Calculator • Enter the test scores for Mr. Pryor’s statistics class on page 116 into L 1 on your calculator. • Press 2 nd , Y= (STAT PLOT) • Turn Plot 1 ON • Select the type on the lower right • Data List: L 1 • Data Axis: x • Mark (doesn’t matter) • Press Zoom, 9: Zoom. Stat • You should have a probability plot!

Using Your Calculator for Ch. 2 • Finding areas with Shade. Norm – Follow the instructions in the Technology Toolbox on page 165 – Notice that the interval in order to find the proportion greater than 125 is (125, 1 E 99, 100, 15). That is because there is no “infinity” option on your calculator. – How would you find the area to the left of 125?

Using your calculator: Finding Areas with normalcdf • You can also find the areas under the Normal curve using normalcdf. This method is quicker than shadenorm, but it does not give us a visual. • Complete the technology toolbox on page 166 • What if we wanted the area between 125 and 140? • Be sure to note that if you are given the standardized scores, you only need to specify the left and right endpoints of the interval you are looking for – i. e. , normalcdf(-2, 1) gives us. 818. This means that the area from z=-2 to z=1 is approximately. 818.

Using Your Calculator: inv. Norm • Finally, we can use our calculators to calculate raw or standardized values given the area under the Normal curve or a relative frequency. • Complete the technology toolbox on page 167 to find the WISC score that has 90% of the scores below it. • Notice that we enter (. 9, 100, 15) to get the raw data score and we enter just (. 9) to get the standardized score.

Next time in Statistics AP • The Chapter 2 Test is on WEDENSDAY • You will need your graphing calculator • Homework: Read the Chapter Summary on p. 161 – 162. • Exercises: 2. 37, 2. 40, 2. 45, 2. 50, 2. 51, 2. 54, 2. 55, 2. 58 2. 61, 2. 63