Chapter 2 2 Programming Language Definition Summary Syntax

Chapter 2. 2 Programming Language Definition

Summary • Syntax and Semantics • Semantics definition – Denotational Semantics – Elementary actions • Syntax definitions – Backus-Naur Formalism – Syntax diagrams

Syntax and Semantics • Syntax = form • Semantics = meaning • Example – My beer is on the table • Syntax : OK • Semantics : OK – My table is on the beer • Syntax : OK • Semantics : You had too many beers !!!

Summary • Syntax and Semantics • Semantics definition – Denotational Semantics – Elementary actions • Syntax definitions – Backus-Naur Formalism – Syntax diagrams

Summary • Syntax and Semantics • Semantics definition – Denotational Semantics – Elementary actions • Syntax definitions – Backus-Naur Formalism – Syntax diagrams

Backus Naur Formalism (BNF) • Terminal Symbols – Appear literally in program text – Examples : “a”, “ 3”, “END”, “>”, “: =” • Non-terminal Symbols – Name given to set of terminal symbols – Written between < and > – Defined by a metalinguistic expression – Examples : <Letter> , <Digit>, <Expression>, <Module> • Metalinguistic expression – Formal definition (: : =) of a non-terminal symbol – Contains terminal and non-terminal symbols – Expresses juxtaposition or choice (the | operator) – Example : <Digit> : : = 0|1|2|3|4|5|6|7|8|9

Backus Naur Formalism (BNF) Examples <Upper. Case. Letter> : : = A|B|C|D|E| |X|Y|Z <Lower. Case. Letter> : : = a|b|c|d|e| |x|y|z <Letter> : : = <Upper. Case. Letter> | <Lower. Case. Letter> <Digit> : : = 1|2|3|4|5|6|7|8|9|0 <Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> <Integer. Number> : : = <Cardinal. Number> | + <Cardinal. Number> | - <Cardinal. Number> <Identifier> : : = <Letter> | <Identifier> <Digit>

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it a digit ? Certainly not

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ?

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ? Is it a digit ? Certainly not

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ? Is it Digit followed by a Cardinal. Number ? Is 3 a Cardinal Number ?

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ? Is it Digit followed by a Cardinal. Number ? Is 3 a Cardinal Number ? Is it a digit ? YES

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ? Is it Digit followed by a Cardinal. Number ? Is 3 a Cardinal. Number ? Is it a digit ? YES As a consequence, 3 is a Cardinal. Number

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ? Is it Digit followed by a Cardinal. Number ? Is 3 a Cardinal. Number ? Is it a digit ? YES As a consequence, 3 is a Cardinal. Number As a consequence, 23 is a Cardinal. Number

<Cardinal. Number> : : = <Digit> | <Digit><Cardinal. Number> Is 123 a Cardinal. Number ? Is it Digit followed by a Cardinal. Number ? Is 23 a Cardinal Number ? Is it Digit followed by a Cardinal. Number ? Is 3 a Cardinal. Number ? Is it a digit ? YES As a consequence, 3 is a Cardinal. Number As a consequence, 23 is a Cardinal. Number As a consequence, 123 is a Cardinal. Number

<Identifier> : : = <Letter> | <Identifier> <Digit> • Correct identifiers – Length, Width, Cost, . . . – My. Salary, Number. Of. Students, Year 1, … – X 1, Y 2, A 1, A 5, … • Incorrect identifiers – My Salary, Number-of-students, … – 1 st. Year, . . .

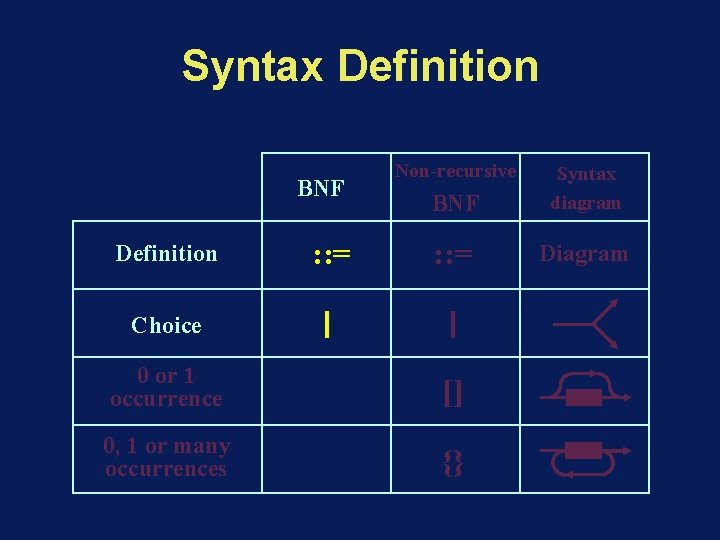
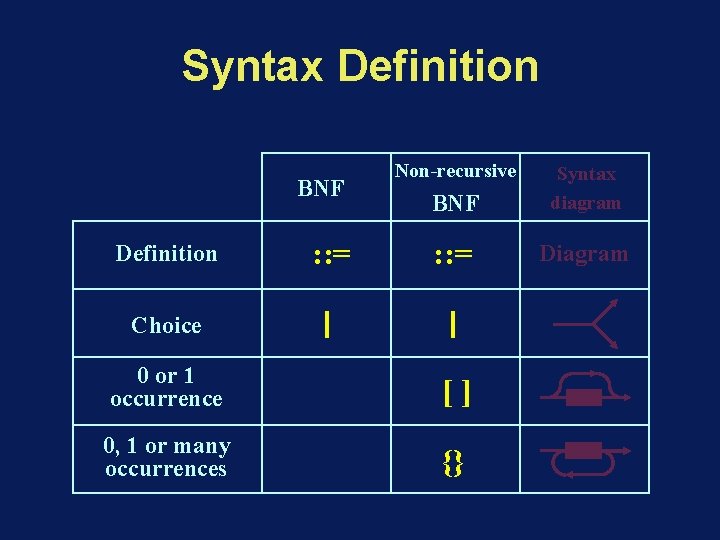
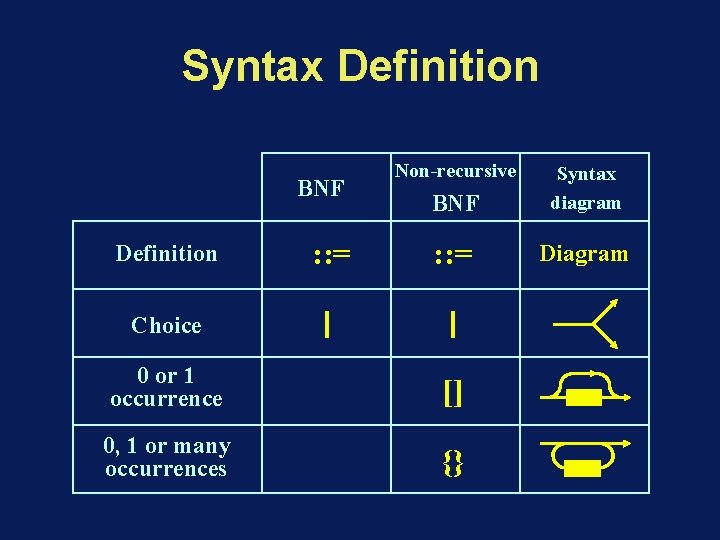
Syntax Definition BNF Definition : : = Non-recursive BNF Syntax diagram : : = Diagram Choice 0 or 1 occurrence [] 0, 1 or many occurrences {}

Syntax Definition BNF Definition : : = Non-recursive BNF Syntax diagram : : = Diagram Choice 0 or 1 occurrence [] 0, 1 or many occurrences {}

Backus Naur Formalism (BNF) Examples <Upper. Case. Letter> : : = A|B|C|D|E| |X|Y|Z <Lower. Case. Letter> : : = a|b|c|d|e| |x|y|z <Letter> : : = <Upper. Case. Letter> | <Lower. Case. Letter> <Digit> : : = 1|2|3|4|5|6|7|8|9|0 <Cardinal. Number> : : = <Digit> {<Digit>} <Integer. Number> : : = [+|-]<Cardinal. Number> <Identifier> : : = <Letter> {<Letter>|<Digit>}

Summary • Syntax and Semantics • Semantics definition – Denotational Semantics – Elementary actions • Syntax definitions – Backus-Naur Formalism – Syntax diagrams

Backus Naur Formalism (BNF) • Terminal Symbols Terminal symbol • Non-terminal Symbols Non-terminal symbol • Metalinguistic expression – Railroad diagrams with semaphores requiring specific symbols to grant passage. – The defined non-terminal symbol leaves all its symbols, in the order of occurrence, at appropriate semaphores and reaches the exit with none left.

Syntax Definition BNF Definition : : = Non-recursive BNF Syntax diagram : : = Diagram Choice 0 or 1 occurrence [] 0, 1 or many occurrences {}

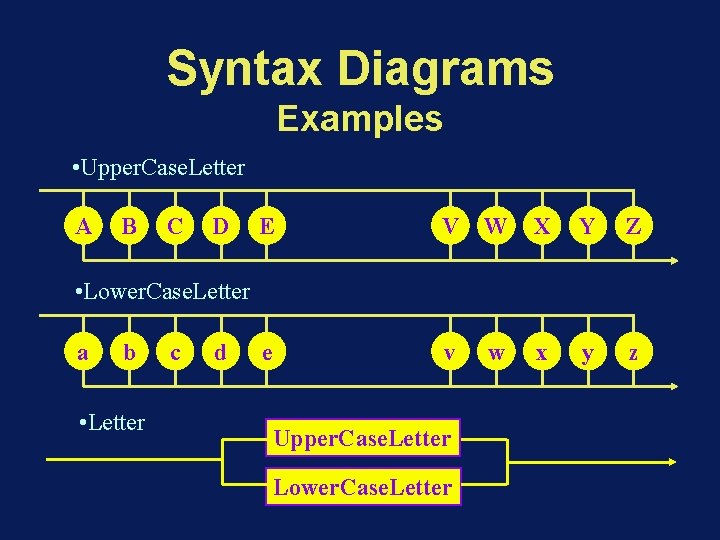
Syntax Diagrams Examples • Upper. Case. Letter A B C D E V W X Y Z e v w x y z • Lower. Case. Letter a b • Letter c d Upper. Case. Letter Lower. Case. Letter

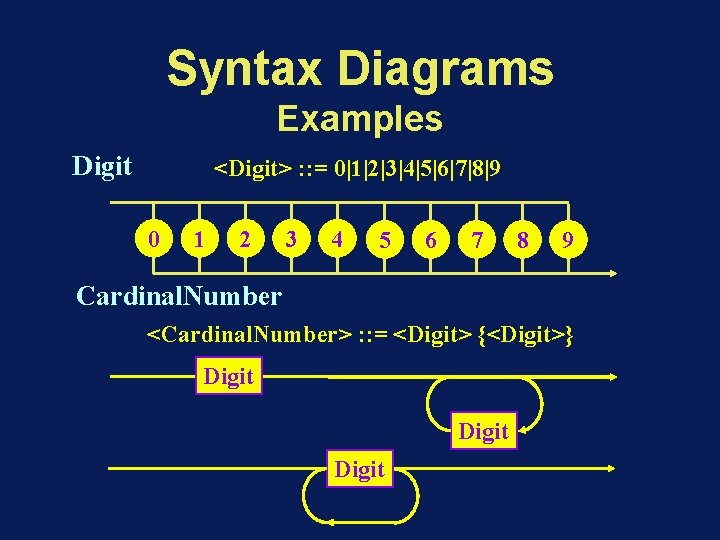
Syntax Diagrams Examples Digit <Digit> : : = 0|1|2|3|4|5|6|7|8|9 0 1 2 3 4 5 6 7 8 9 Cardinal. Number <Cardinal. Number> : : = <Digit> {<Digit>} Digit

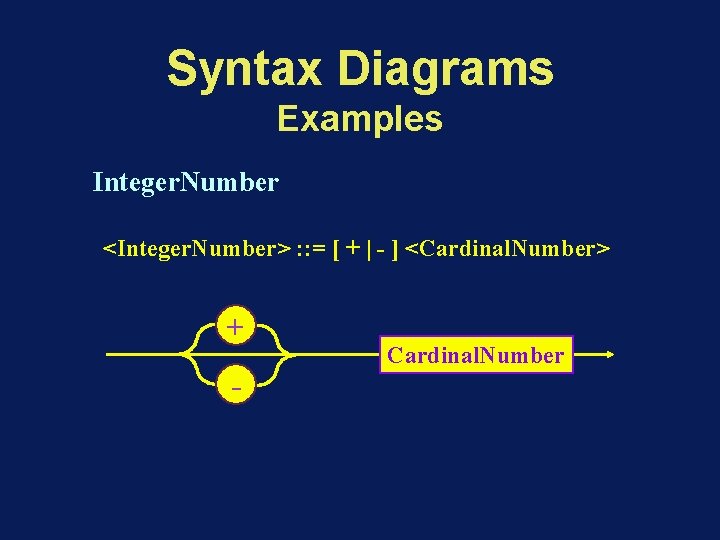
Syntax Diagrams Examples Integer. Number <Integer. Number> : : = [ + | - ] <Cardinal. Number> + - Cardinal. Number

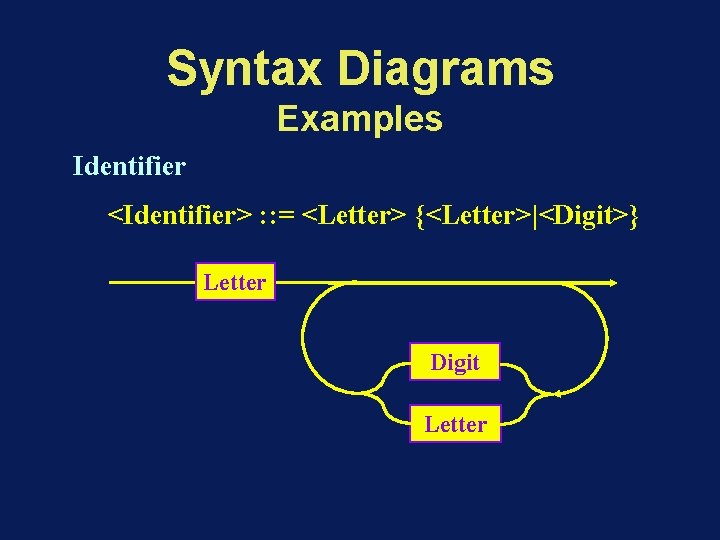
Syntax Diagrams Examples Identifier <Identifier> : : = <Letter> {<Letter>|<Digit>} Letter Digit Letter

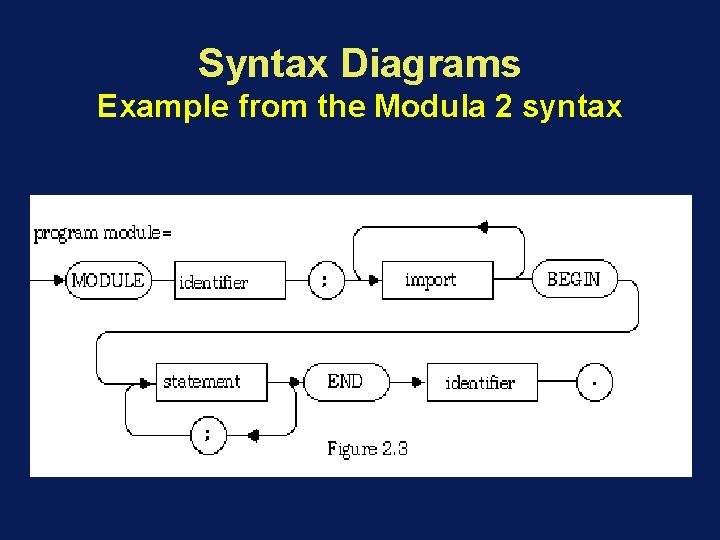
Syntax Diagrams Example from the Modula 2 syntax