Chapter 19 Ionic Equilibria in Aqueous Systems 19

Chapter 19 Ionic Equilibria in Aqueous Systems 19 -1

Ionic Equilibria in Aqueous Systems 19. 1 Equilibria of acid-base buffer systems 19. 2 Acid-base titration curves 19. 3 Equilibria of slightly soluble ionic compounds 19. 4 Equilibria involving complex ions 19. 5 Application of ionic equilibria to chemical analysis 19 -2

The effect of addition of acid or base to … acid added base added an unbuffered solution. acid added Figure 19. 1 19 -3 base added a buffered solution. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Acid-Base Buffer Systems Buffers function by reducing changes in [H 3 O+] that result from additions of acid or base to the solution. Buffers are composed of the conjugate acid-base pair of a weak acid. Buffers function via the common ion effect. CH 3 COOH(aq) + H 2 O(l) CH 3 COO-(aq) + H 3 O+(aq) The common ion effect occurs when a reactant containing a given ion is added to an equilibrium mixture that already contains that ion and the position of the equilibrium shifts away from forming more of it. 19 -4

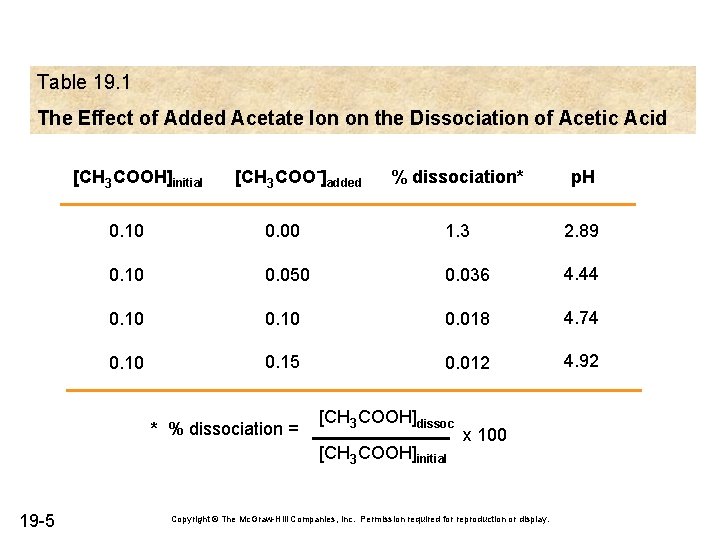
Table 19. 1 The Effect of Added Acetate Ion on the Dissociation of Acetic Acid [CH 3 COOH]initial [CH 3 COO-]added % dissociation* p. H 0. 10 0. 00 1. 3 2. 89 0. 10 0. 050 0. 036 4. 44 0. 10 0. 018 4. 74 0. 10 0. 15 0. 012 4. 92 * % dissociation = [CH 3 COOH]dissoc [CH 3 COOH]initial 19 -5 x 100 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

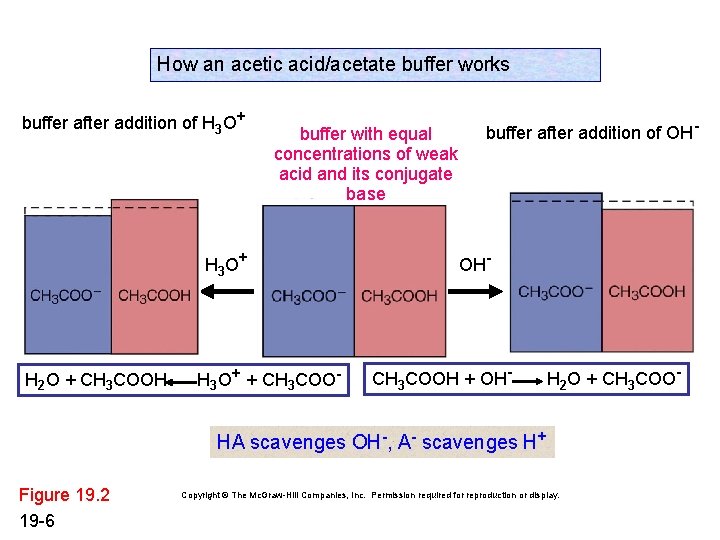
How an acetic acid/acetate buffer works buffer after addition of H 3 O+ buffer with equal concentrations of weak acid and its conjugate base H 3 O + H 2 O + CH 3 COOH H 3 O+ + CH 3 COO- buffer after addition of OH- CH 3 COOH + OH- H 2 O + CH 3 COO- HA scavenges OH-, A- scavenges H+ Figure 19. 2 19 -6 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Some Details Ka = [CH 3 COO-][H 3 O+]/[CH 3 COOH] [H 3 O+] = Ka x [CH 3 COOH]/[CH 3 COO-] Since Ka is constant, [H 3 O+] depends directly on the ratio of the concentrations of HA and its conjugate base, A-. 19 -7

Sample Problem 19. 1 PROBLEM: Calculating the effect of added H 3 O+ and OHon buffer p. H Calculate the p. H of the following solutions. (a) A buffer solution consisting of 0. 50 M CH 3 COOH and 0. 50 M CH 3 COONa (b) After adding 0. 020 mol of solid Na. OH to 1. 0 L of the buffer solution in part (a) (c) After adding 0. 020 mol of HCl to 1. 0 L of the buffer solution in part (a) Ka of CH 3 COOH = 1. 8 x 10 -5 (assume the additions cause negligible volume changes) PLAN: We know Ka and can find initial concentrations of conjugate acid and base. Make assumptions about the amount of acid dissociating relative to its initial concentration. Proceed stepwise through changes in the system. SOLUTION: concentration (M) initial (a) CH 3 COOH(aq) + H 2 O(l) 0. 50 -x - CH 3 COO-(aq) + H 3 O+(aq) 0. 50 +x change equilibrium 0. 50 - x 0. 50 + x x ______________________________ 19 -8

Sample Problem 19. 1 (continued) [H 3 O+] = x Ka = [CH 3 COO-]eq ≈ 0. 50 M [CH 3 COOH]eq ≈ 0. 50 M [H 3 O+][CH 3 COO-] [H 3 O+] = x = Ka [CH 3 COOH] [CH 3 COO-] Check the assumption: 1. 8 x 10 -5/0. 50 (b) [OH-]added = concentration (M) before addition after addition 0. 020 mol 1. 0 L soln p. H = 4. 74 100 = 3. 6 x 10 -3 % = 0. 020 M Na. OH CH 3 COOH(aq) + OH-(aq) 0. 50 0. 48 X = 1. 8 x 10 -5 M 0. 020 0 CH 3 COO-(aq) + H 2 O (l) 0. 50 0. 52 - ______________________________ 19 -9

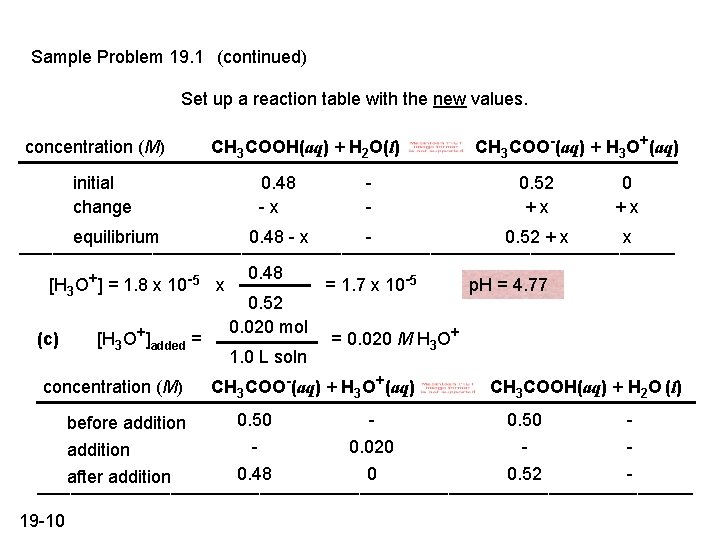
Sample Problem 19. 1 (continued) Set up a reaction table with the new values. concentration (M) CH 3 COOH(aq) + H 2 O(l) initial change 0. 48 -x - CH 3 COO-(aq) + H 3 O+(aq) 0. 52 +x 0 +x equilibrium 0. 48 - x 0. 52 + x x ______________________________ [H 3 O+] = 1. 8 x 10 -5 x (c) [H 3 O+]added = concentration (M) 0. 48 0. 52 0. 020 mol 1. 0 L soln = 1. 7 x 10 -5 p. H = 4. 77 = 0. 020 M H 3 O+ CH 3 COO-(aq) + H 3 O+(aq) CH 3 COOH(aq) + H 2 O (l) 0. 50 before addition 0. 020 addition 0. 48 0 0. 52 after addition ______________________________ 19 -10

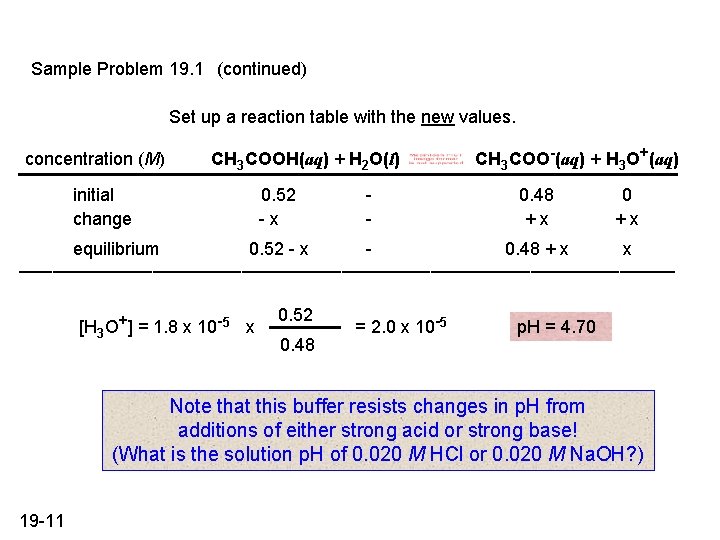
Sample Problem 19. 1 (continued) Set up a reaction table with the new values. concentration (M) CH 3 COOH(aq) + H 2 O(l) initial change equilibrium CH 3 COO-(aq) + H 3 O+(aq) 0. 52 -x - 0. 48 +x 0. 52 - x - 0. 48 + x x ______________________________ [H 3 O+] = 1. 8 x 10 -5 x 0. 52 0. 48 = 2. 0 x 10 -5 p. H = 4. 70 Note that this buffer resists changes in p. H from additions of either strong acid or strong base! (What is the solution p. H of 0. 020 M HCl or 0. 020 M Na. OH? ) 19 -11

The Henderson-Hasselbalch Equation An equation that relates p. H, p. Ka and the ratio of weak acid to its conjugate base for a buffer solution. H 3 O+ + A - HA + H 2 O Ka = [H 3 O+][A-]/[HA] [H 3 O+] = Ka x [HA]/[A-] -log [H 3 O+] = -log Ka - log ([HA]/[A-]) p. H = p. Ka + log ([A-]/[HA]) or p. H = p. Ka + log ([base]/[acid]) Special case: when [base] = [acid], the p. H of the buffer solution equals the p. Ka of the weak acid. 19 -12

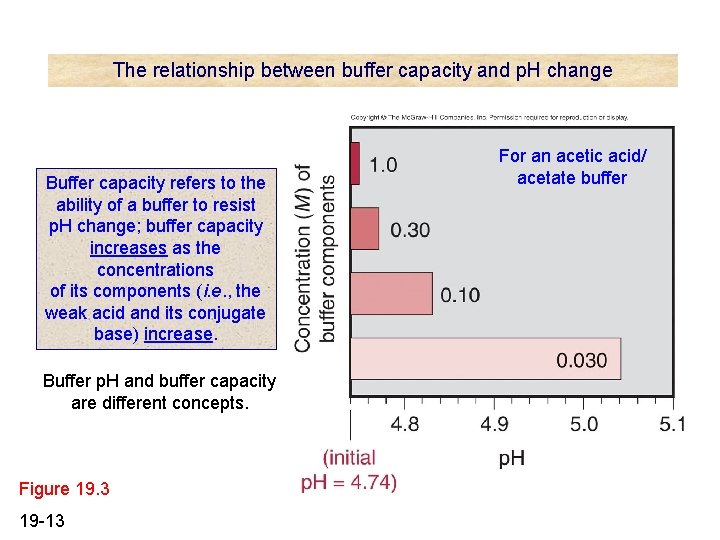
The relationship between buffer capacity and p. H change Buffer capacity refers to the ability of a buffer to resist p. H change; buffer capacity increases as the concentrations of its components (i. e. , the weak acid and its conjugate base) increase. Buffer p. H and buffer capacity are different concepts. Figure 19. 3 19 -13 For an acetic acid/ acetate buffer

Key Concepts For a given addition of acid or base, the concentration ratio ([A]/[HA]) changes less for similar buffer component concentrations than it does for different concentrations. A buffer has the highest capacity when the concentrations of HA and A- are equal. A buffer whose p. H is equal to or near the p. Ka of its acid component has the highest buffer capacity. Buffer range: the p. H range over which the buffer acts effectively; defined as p. Ka +/- 1 p. H unit 19 -14

Sample Problem 19. 2 PROBLEM: PLAN: Preparing a buffer An environmental chemist needs a carbonate buffer of p. H 10. 00 to study the effects of acid rain on limestone-rich soils. How many grams of Na 2 CO 3 must she add to 1. 5 L of freshly prepared 0. 20 M Na. HCO 3 to prepare the buffer? Ka of HCO 3 - is 4. 7 x 10 -11. We know the Ka and the conjugate acid-base pair. Convert p. H to [H 3 O+], find the number of moles of carbonate and convert to mass. SOLUTION: [CO 32 -][H 3 O+] HCO 3 -(aq) + H 2 O(l) CO 32 -(aq) + H 3 O+(aq) p. H = 10. 00; [H 3 O+] = 1. 0 x 10 -10 4. 7 x 10 -11 = [CO 32 -][10 -10] [0. 20] moles of Na 2 CO 3 = (1. 5 L)(0. 094 mol/L) = 0. 14 moles x 19 -15 105. 99 g mol Ka = = 15 g Na 2 CO 3 [HCO 3 -] [CO 32 -] = 0. 094 M

Acid-Base Titration Curves Acid-Base Indicator: a weak organic acid (HIn) that has a different color than its conjugate base (In-); small amounts are used in acid-base titrations; change color over different p. H ranges 19 -16

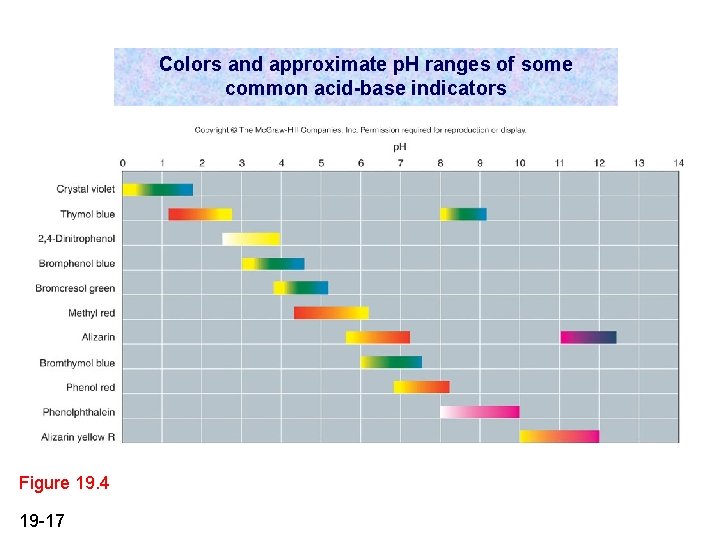
Colors and approximate p. H ranges of some common acid-base indicators Figure 19. 4 19 -17

The color change of the indicator bromthymol blue p. H 7. 5 p. H 6 Figure 19. 5 acidic 19 -18 basic change occurs over ~2 p. H units Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

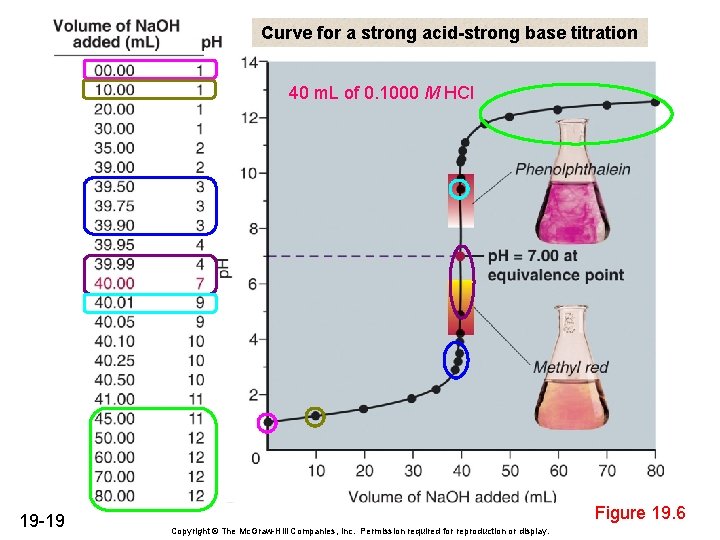
Curve for a strong acid-strong base titration 40 m. L of 0. 1000 M HCl 19 -19 Figure 19. 6 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

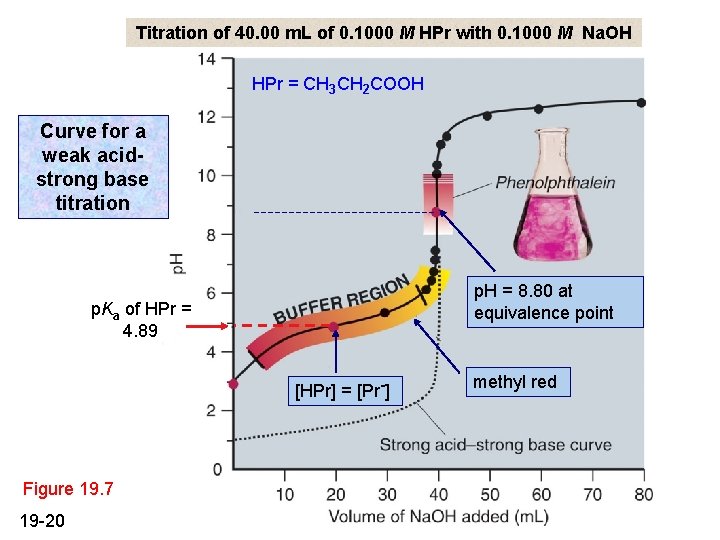
Titration of 40. 00 m. L of 0. 1000 M HPr with 0. 1000 M Na. OH HPr = CH 3 CH 2 COOH Curve for a weak acidstrong base titration p. H = 8. 80 at equivalence point p. Ka of HPr = 4. 89 [HPr] = [Pr-] Figure 19. 7 19 -20 methyl red

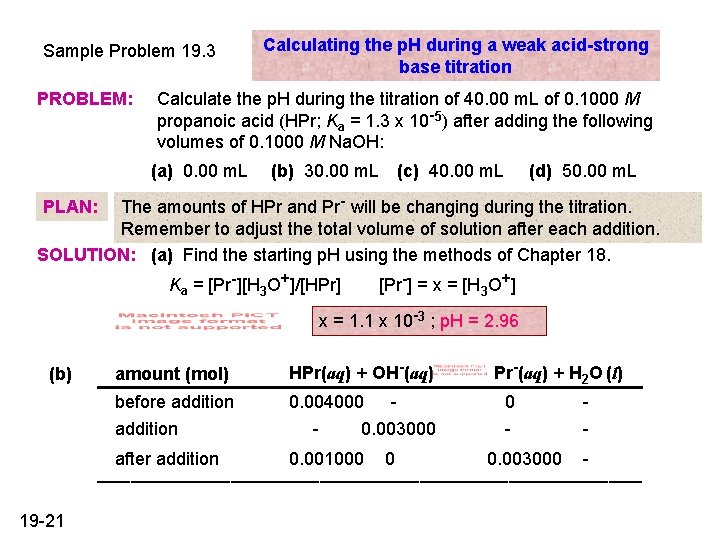
Sample Problem 19. 3 PROBLEM: Calculating the p. H during a weak acid-strong base titration Calculate the p. H during the titration of 40. 00 m. L of 0. 1000 M propanoic acid (HPr; Ka = 1. 3 x 10 -5) after adding the following volumes of 0. 1000 M Na. OH: (a) 0. 00 m. L (b) 30. 00 m. L (c) 40. 00 m. L (d) 50. 00 m. L The amounts of HPr and Pr- will be changing during the titration. Remember to adjust the total volume of solution after each addition. SOLUTION: (a) Find the starting p. H using the methods of Chapter 18. PLAN: Ka = [Pr-][H 3 O+]/[HPr] [Pr-] = x = [H 3 O+] x = 1. 1 x 10 -3 ; p. H = 2. 96 (b) amount (mol) HPr(aq) + OH-(aq) before addition 0. 004000 0. 003000 after addition 0. 001000 0 Pr-(aq) + H 2 O (l) 0 0. 003000 - _________________________ 19 -21

Sample Problem 19. 3 (continued) [H 3 O+] = 1. 3 x 10 -5 x 0. 001000 mol 0. 003000 mol = 4. 3 x 10 -6 M p. H = 5. 37 (c) When 40. 00 m. L of Na. OH are added, all of the HPr will be reacted and the [Pr-] will be: 0. 004000 mol = 0. 05000 M 0. 04000 L + 0. 04000 L Ka x Kb = Kw/Ka = 1. 0 x 10 -14/1. 3 x 10 -5 = 7. 7 x 10 -10 [H 3 O+] = Kw / = 1. 6 x 10 -9 M p. H = 8. 80 (d) 50. 00 m. L of Na. OH will produce an excess of OH-. mol excess OH- = (0. 1000 M)(0. 05000 L - 0. 04000 L) = 0. 00100 mol [H 3 O+] = 1. 0 x 10 -14/0. 01111 = 9. 0 x 10 -13 M p. H = 12. 05 19 -22 M = 0. 00100 mol 0. 0900 L M = 0. 01111

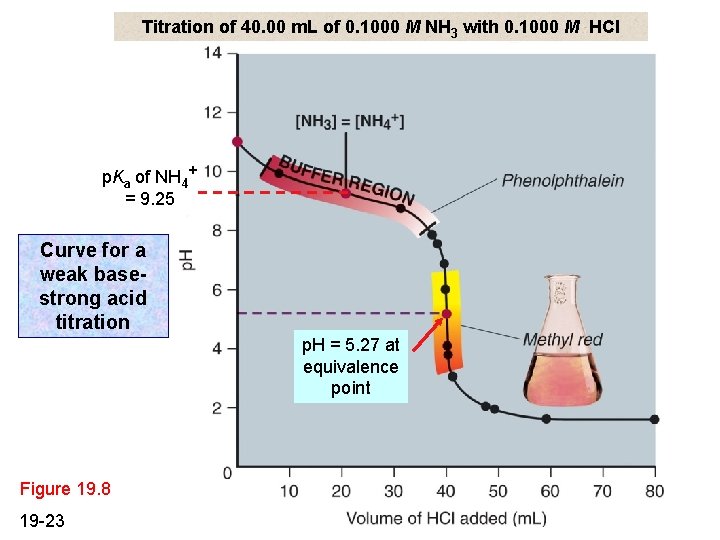
Titration of 40. 00 m. L of 0. 1000 M NH 3 with 0. 1000 M HCl p. Ka of NH 4+ = 9. 25 Curve for a weak basestrong acid titration p. H = 5. 27 at equivalence point Figure 19. 8 19 -23

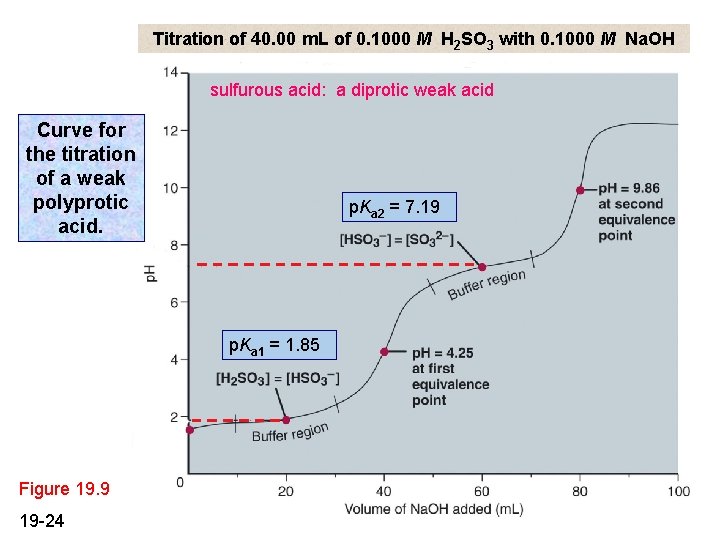
Titration of 40. 00 m. L of 0. 1000 M H 2 SO 3 with 0. 1000 M Na. OH sulfurous acid: a diprotic weak acid Curve for the titration of a weak polyprotic acid. p. Ka 2 = 7. 19 p. Ka 1 = 1. 85 Figure 19. 9 19 -24

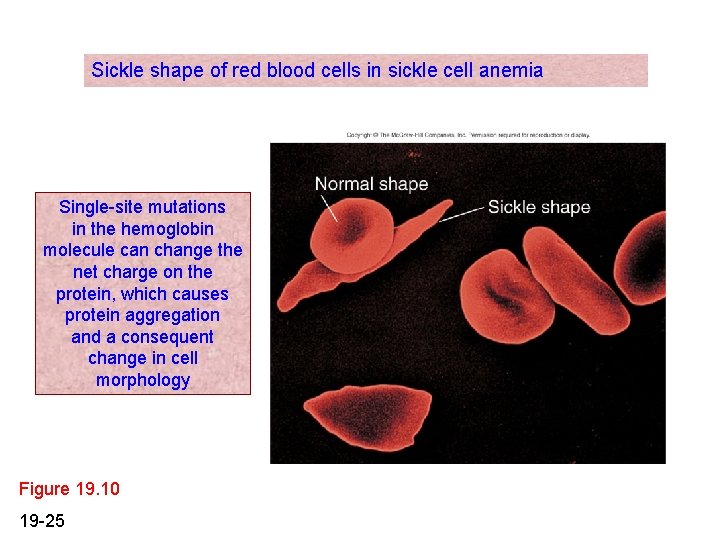
Sickle shape of red blood cells in sickle cell anemia Single-site mutations in the hemoglobin molecule can change the net charge on the protein, which causes protein aggregation and a consequent change in cell morphology Figure 19. 10 19 -25

Dealing with Solubility Equilibria Slightly soluble ionic compounds Ion-Product Expressions (Qsp); Solubility-Product Constants (Ksp) Pb. SO 4(s) Pb 2+(aq) + SO 42 -(aq) Qc = [Pb 2+][SO 4 2 -]/[Pb. SO 4] Qsp = [Pb 2+][SO 42 -] At saturation, Qsp attains a constant value (equilibrium has been established); thus, Qsp = Ksp Generally, for a saturated solution of a slightly soluble ionic compound with formula Mp. Xq: Qsp = [Mn+]p[Xz-]q = Ksp 19 -26

A slightly soluble ionic compound Pb. Cl 2 19 -27

Writing ion-product expressions for slightly soluble ionic compounds Sample Problem 19. 4 PROBLEM: Write the ion-product expression for each of the following: (a) magnesium carbonate (c) calcium phosphate PLAN: (b) iron(II) hydroxide (d) silver sulfide Write an equation which describes a saturated solution. Take note of the unusual behavior of the sulfide ion produced in (d). SOLUTION: (a) Mg. CO 3(s) (b) Fe(OH)2(s) 2 -(aq) Mg 2+(aq) + CO 3� Fe 2+(aq) + 2 OH- (aq) 19 -28 Ksp = [Ca 2+]3[PO 43 -]2 2 -(aq) 2 Ag+(aq) + S� S 2 -(aq) + H 2 O(l) Ag 2 S(s) + H 2 O(l) Ksp = [Fe 2+][OH-]2 3 Ca 2+(aq) + 2 PO 43 -(aq) (c) Ca 3(PO 4)2(s) (d) Ag 2 S(s) Ksp = [Mg 2+][CO 32 -] HS-(aq) + OH-(aq) 2 Ag+(aq) + HS-(aq) + OH-(aq) Ksp = [Ag+]2[HS-][OH-]

Table 19. 2 Solubility-Product Constants (Ksp) of Selected Ionic Compounds at 25 o. C Name and Formula Ksp aluminum hydroxide, Al(OH)3 3 x 10 -34 cobalt(II) carbonate, Co. CO 3 1. 0 x 10 -10 iron(II) hydroxide, Fe(OH)2 4. 1 x 10 -15 lead(II) fluoride, Pb. F 2 3. 6 x 10 -8 lead(II) sulfate, Pb. SO 4 1. 6 x 10 -8 mercury(I) iodide, Hg 2 I 2 4. 7 x 10 -29 silver sulfide, Ag 2 S 8 x 10 -48 zinc iodate, Zn(IO 3)2 3. 9 x 10 -6 The magnitude of Ksp is a measure of how far to the right the dissolution proceeds at equilibrium (i. e. , at saturation). 19 -29 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Sample Problem 19. 5 Determining Ksp from solubility data PROBLEM: (a) Lead(II) sulfate is a key component in car batteries. Its solubility in water at 25 o. C is 4. 25 x 10 -3 g/100 m. L solution. What is the Ksp of Pb. SO 4? (b) When lead(II) fluoride (Pb. F 2) is shaken with pure water at 25 o. C, the solubility is found to be 0. 64 g/L. Calculate the Ksp of Pb. F 2. PLAN: Write the dissolution equation; find moles of dissociated ions; convert solubility to M and substitute values into the solubility product constant expression. SOLUTION: (a) Pb. SO 4(s) 4. 25 x 10 -3 g 100 m. L soln x 1000 m. L L Pb 2+(aq) + SO 42 -(aq) x mol Pb. SO 4 303. 3 g Pb. SO 4 Ksp = [Pb 2+][SO 42 -] = 1. 40 x 10 -4 M Pb. SO 4 Ksp = [Pb 2+][SO 42 -] = (1. 40 x 10 -4)2 = 1. 96 x 10 -8 19 -30

Sample Problem 19. 5 (continued) Pb 2+(aq) + 2 F-(aq) (b) Pb. F 2(s) 0. 64 g L soln x Ksp = [Pb 2+][F-]2 mol Pb. F 2 245. 2 g Pb. F 2 = 2. 6 x 10 -3 M Pb. F 2 Ksp = (2. 6 x 10 -3)(5. 2 x 10 -3)2 = 7. 0 x 10 -8 [Pb 2+] 19 -31 [F-]

Sample Problem 19. 6 Determining solubility from Ksp PROBLEM: Calcium hydroxide is a major component of mortar, plaster and cement, and solutions of Ca(OH)2 are used in industry as a cheap, strong base. Calculate the solubility of Ca(OH)2 in water at 25 o. C if its Ksp is 6. 5 x 10 -6. PLAN: Write a dissociation equation and Ksp expression; find the molar solubility (S) using a table. SOLUTION: Ca 2+(aq) + 2 OH-(aq) Ca(OH)2(s) concentration (M) Ca(OH)2(s) Ksp = [Ca 2+][OH-]2 Ca 2+(aq) + 2 OH-(aq) initial - 0 0 change - +S + 2 S equilibrium - S 2 S __________________________ Ksp = (S)(2 S)2 = 4 S 3 19 -32 S= = 1. 2 x 10 -2 M

Ksp and Solubilities Ksp values are used to determine relative solubilities provided that comparisons are made between compounds whose formulas contain the same total number of ions. The compound having the higher Ksp is more soluble. 19 -33

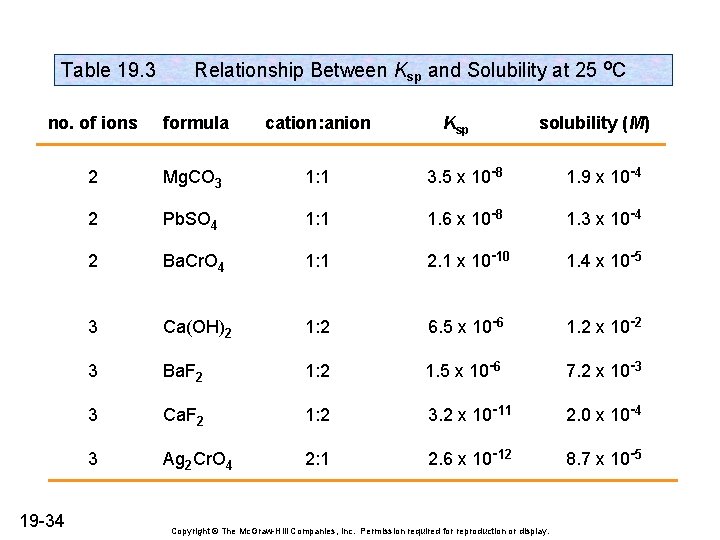
Table 19. 3 Relationship Between Ksp and Solubility at 25 o. C no. of ions formula cation: anion 2 Mg. CO 3 1: 1 3. 5 x 10 -8 1. 9 x 10 -4 2 Pb. SO 4 1: 1 1. 6 x 10 -8 1. 3 x 10 -4 2 Ba. Cr. O 4 1: 1 2. 1 x 10 -10 1. 4 x 10 -5 3 Ca(OH)2 1: 2 6. 5 x 10 -6 1. 2 x 10 -2 3 Ba. F 2 1: 2 1. 5 x 10 -6 7. 2 x 10 -3 3 Ca. F 2 1: 2 3. 2 x 10 -11 2. 0 x 10 -4 3 Ag 2 Cr. O 4 2: 1 2. 6 x 10 -12 8. 7 x 10 -5 19 -34 Ksp solubility (M) Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Common Ion Effects on Solubility The presence of a common ion decreases the solubility of a slightly soluble ionic compound. Pb. Cr. O 4(s) Pb 2+(aq) + Cr. O 42 -(aq) Add Na 2 Cr. O 4 (a very soluble salt; a strong electrolyte) Result: equilibrium shifts to the left (Le. Châtelier’s principle) 19 -35

The effect of a common ion on solubility Cr. O 42 - added Pb. Cr. O 4(s) Pb 2+(aq) + Cr. O 42 -(aq) Figure 19. 11 19 -36 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Calculating the effect of a common ion on solubility Sample Problem 19. 7 PROBLEM: In Sample Problem 19. 6, we calculated the solubility of Ca(OH)2 in water. What is its solubility in 0. 10 M Ca(NO 3)2? Ksp of Ca(OH)2 is 6. 5 x 10 -6. PLAN: Set up a reaction equation and table for the dissolution of Ca(OH)2. The Ca(NO 3)2 will supply extra [Ca 2+], which will influence the solubility of the Ca(OH)2 through the common ion effect. SOLUTION: concentration (M) Ca(OH)2(s) Ca 2+(aq) + 2 OH-(aq) initial - 0. 10 0 change - +S +2 S equilibrium - 0. 10 + S 2 S _______________________ Ksp = 6. 5 x 10 -6 = (0. 10 + S)(2 S)2 = (0. 10)(2 S)2 S ≈ (6. 5 x 10 -5/4)0. 5 19 -37 -3 M = 4. 0 x 10� = 1. 2 x 10 -2 M (S << 0. 10) Check the assumption: -3 M 4. 0 x 10� x 100 = 4. 0 % 0. 10 M

The Effect of p. H on Solubility If the compound contains the anion of a weak acid, addition of H 3 O+ (from a strong acid) increases its solubility (Le. Châtelier’s principle) Ca. CO 3(s) Ca 2+(aq) + CO 32 -(aq) + H 3 O+(aq) HCO 3 -(aq) + H 3 O+(aq) H 2 CO 3(aq) HCO 3 - (aq) + H 2 O(l) H 2 CO 3(aq) + H 2 O(l) 2 H 2 O(l) + CO 2(g) Adding H 3 O+ shifts the equilibrium to the right. 19 -38

Test for the presence of a carbonate Effect of the addition of a strong acid (release of carbon dioxide) Figure 19. 12 19 -39

Predicting the effect of adding a strong acid on solubility Sample Problem 19. 8 PROBLEM: Write balanced equations to explain whether addition of H 3 O+ from a strong acid will affect the solubility of the following ionic compounds: (a) lead(II) bromide (b) copper(II) hydroxide (c) iron(II) sulfide PLAN: Write dissolution equations and consider how strong acid would affect the anion component. SOLUTION: (a) Pb. Br 2(s) Pb 2+(aq) + 2 Br-(aq) Br- is the anion of a strong acid. (b) Cu(OH)2(s) No effect. Cu 2+(aq) + 2 OH-(aq) The OH- reacts with the added hydronium ion to form water. The equilibrium will shift to the right and thus solubility will increase. 2 will Fe 2+(aq) + S 2 -(aq) S is the anion of a weak acid and react with water to produce OH. Fe. S(s) + H 2 O(l) Fe 2+(aq) + HS-(aq) + OH-(aq) (c) Fe. S(s) 19 -40 Both weak acids serve to increase the solubility of Fe. S.

Predicting Whether a Precipitate Will Form Compare Qsp with Ksp. When Qsp = Ksp, the solution is saturated and no change occurs. When Qsp > Ksp, a precipitate forms until the solution is saturated. When Qsp < Ksp, the solution is unsaturated and no precipitate forms. 19 -41

Sample Problem 19. 9 PROBLEM: PLAN: Predicting whether a precipitate will form A common laboratory method for preparing a precipitate is to mix solutions of the component ions. Does a precipitate form when 0. 100 L of 0. 30 M Ca(NO 3)2 is mixed with 0. 200 L of 0. 060 M Na. F? Write out a reaction equation to see which salt could form. Look up the Ksp values in a table. Treat this as a reaction quotient, Q, problem and calculate whether the concentrations of ions are > or < Ksp. Remember to consider the final diluted solution when calculating concentrations. SOLUTION: Ca. F 2(s) Ca 2+(aq) + 2 F-(aq) Ksp = 3. 2 x 10 -11 mol Ca 2+ = 0. 100 L(0. 30 mol/L) = 0. 030 mol [Ca 2+] = 0. 030 mol/0. 300 L = 0. 10 M mol F- = 0. 200 L(0. 060 mol/L) = 0. 012 mol [F-] = 0. 012 mol/0. 300 L = 0. 040 M Q = [Ca 2+][F-]2 = (0. 10)(0. 040)2 = 1. 6 x 10 -4 Q is >> Ksp, thus Ca. F 2 will precipitate. 19 -42

Equilibria Involving Complex Ions A complex ion consists of a central metal ion covalently bonded to two or more anions (or molecules) called ligands. Ionic ligands include hydroxide (OH-), chloride (Cl-) and cyanide (CN-) anions. Water, CO and NH 3 are examples of molecular ligands. All complex ions are Lewis adducts. The metal acts as a Lewis acid and the ligand acts as a Lewis base. We will consider equilibria of hydrated ions with ligands other than water. 19 -43

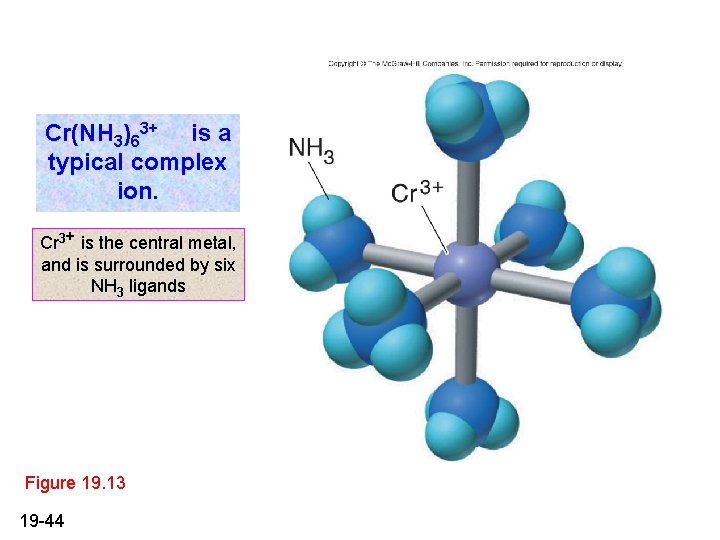
Cr(NH 3)63+ is a typical complex ion. Cr 3+ is the central metal, and is surrounded by six NH 3 ligands Figure 19. 13 19 -44

Formation Constants, Kf, of Complex Ions M(H 2 O)42+(aq) + 4 NH 3(aq) M(NH 3)42+(aq) + 4 H 2 O(l) Kc = [M(NH 3)42+][H 2 O]4/[M(H 2 O)42+][NH 3]4 Kf = Kc/[H 2 O]4 = [M(NH 3)42+]/[M(H 2 O)42+][NH 3]4 In fact, four sequential reactions occur, defined by four Kf values, for the systematic substitution of H 2 O ligands by NH 3 ligands. Thus, Kf = Kf 1 x Kf 2 x Kf 3 x Kf 4 19 -45

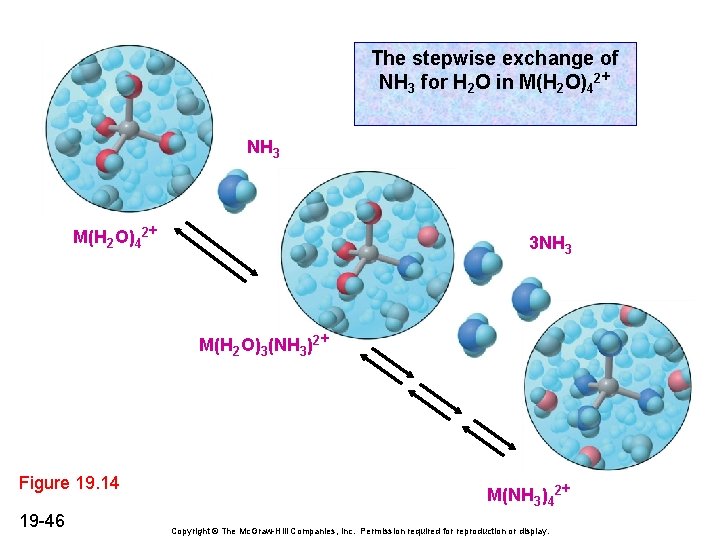
The stepwise exchange of NH 3 for H 2 O in M(H 2 O)42+ NH 3 M(H 2 O)42+ 3 NH 3 M(H 2 O)3(NH 3)2+ Figure 19. 14 19 -46 M(NH 3)42+ Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

19 -47

Sample Problem 19. 10 Calculating the concentration of a complex ion PROBLEM: An industrial chemist converts Zn(H 2 O)42+ to the more stable Zn(NH 3)42+ by mixing 50. 0 L of 0. 0020 M Zn(H 2 O)42+ and 25. 0 L of 0. 15 M NH 3. What is the final [Zn(H 2 O)42+]? Kf of Zn(NH 3)42+ is 7. 8 x 108. PLAN: Write the reaction equation and Kf expression. Use a reaction table to list various concentrations. Remember that components will be diluted when mixed as you calculate final concentrations. The large excess of NH 3 will drive the reaction to completion. SOLUTION: Zn(H 2 O)42+(aq) + 4 NH 3(aq) Kf = [Zn(NH 3)42+] Zn(NH 3)42+(aq) + 4 H 2 O(l) [Zn(H 2 O)42+]initial = (50. 0 L)(0. 0020 M) [Zn(H 2 O)42+][NH 3]4 [NH 3]initial = 75. 0 L (25. 0 L)(0. 15 M) 75. 0 L 19 -48 = 1. 3 x 10 -3 M = 5. 0 x 10 -2 M

Sample Problem 19. 10 (continued) Since we assume that all of the Zn(H 2 O)42+ has reacted, it would consume four times its amount in NH 3. . [NH 3]used = 4 (1. 3 x 10 -3 M) = 5. 2 x 10 -3 M [Zn(H 2 O)42+]remaining = x (a very small amount) concentration (M) Zn(H 2 O)42+(aq) + 4 NH 3(aq) 1. 3 x 10 -3 initial change ~(-1. 3 x 10 -3) equilibrium Zn(NH 3)42+(aq) + 4 H 2 O(l) 5. 0 x 10 -2 ~(-5. 2 x 10 -3) 4. 5 x 10 -2 x 0 - ~(+1. 3 x 10 -3) 1. 3 x 10 -3 - _______________________________ Kf = [Zn(NH 3)42+] [Zn(H 2 O)42+][NH 3]4 7. 8 x 108 = (1. 3 x 10 -3) x (4. 5 x 10 -2)4 x = 4. 1 x 10 -7 M A result of the very large Kf! 19 -49

Solubility Issues A ligand increases the solubility of a slightly soluble ionic compound if it forms a complex ion with the cation. Zn. S(s) + H 2 O(l) Zn 2+(aq) + HS-(aq) + OH-(aq) Ksp = 2. 0 x 10 -22 Upon addition of some 1. 0 M Na. CN: Zn 2+(aq) + 4 CN-(aq) Zn(CN)42+(aq) Kf = 4. 2 x 1019 The overall equation is: Zn. S(s) + 4 CN-(aq) + H 2 O(l) Zn(CN)42+(aq) + HS-(aq) + OH-(aq) Koverall = Ksp x Kf = 8. 4 x 10 -3 19 -50

Sample Problem 19. 11 Calculating the effect of complex ion formation on solubility PROBLEM: In black-and-white film developing, excess Ag. Br is removed from the film negative by “hypo”, an aqueous solution of sodium thiosulfate (Na 2 S 2 O 3), through formation of the complex ion Ag(S 2 O 3)23 -. Calculate the solubility of Ag. Br in (a) H 2 O; (b) 1. 0 M hypo. Kf of Ag(S 2 O 3)23 - is 4. 7 x 1013 and Ksp Ag. Br is 5. 0 x 10 -13. PLAN: Write equations for the reactions involved. Use Ksp to find S, the molar solubility. Consider the shift in the equilibrium upon the addition of the complexing agent. SOLUTION: (a) (b) 19 -51 Ag. Br(s) Ag+(aq) + Br-(aq) Ksp = [Ag+][Br-] = 5. 0 x 10 -13 S = [Ag. Br]dissolved = [Ag+] = [Br-] Ksp = S 2 = 5. 0 x 10 -13; S = 7. 1 x 10 -7 M Ag. Br(s) Ag+(aq) + Br-(aq) Ag+(aq) + 2 S 2 O 32 -(aq) Ag(S 2 O 3)23 -(aq) Ag. Br(s) + 2 S 2 O 32 -(aq) Br-(aq) + Ag(S 2 O 3)23 -(aq)

Sample Problem 19. 11 (continued) [Br-][Ag(S 2 O 3)23 - ] Koverall = Ksp x Kf = = (5. 0 x 10 -13)(4. 7 x 1013)= 24 [S 2 O 32 -]2 concentration (M) Ag. Br(s) + 2 S 2 O 32 -(aq) Br-(aq) + Ag(S 2 O 3)23 -(aq) initial - 1. 0 0 0 change - -2 S +S +S equilibrium - S S 1. 0 - 2 S _____________________________ Koverall = S 2 = 24 (1. 0 - 2 S)2 S 1. 0 - 2 S S = [Ag(S 2 O 3)23 -] = 0. 45 M 19 -52 = (24)1/2

Complex Ions of Amphoteric Hydroxides Amphoteric hydroxides: compounds that dissolve very little in water but to a much greater extent in acidic and basic solutions Al(OH)3(s) Al 3+(aq) + 3 OH-(aq) Ksp = 3 x 10 -34 Al(OH)3 dissolves in acid: 3 H 3 O+(aq) + 3 OH- (aq) Al(OH)3(s) + 3 H 3 O+(aq) 6 H 2 O(l) Al 3+(aq) + 6 H 2 O(l) Al(OH)3 dissolves in base through the formation of a complex ion: Al(OH)3(s) + OH-(aq) 19 -53 Al(OH)4 -(aq)

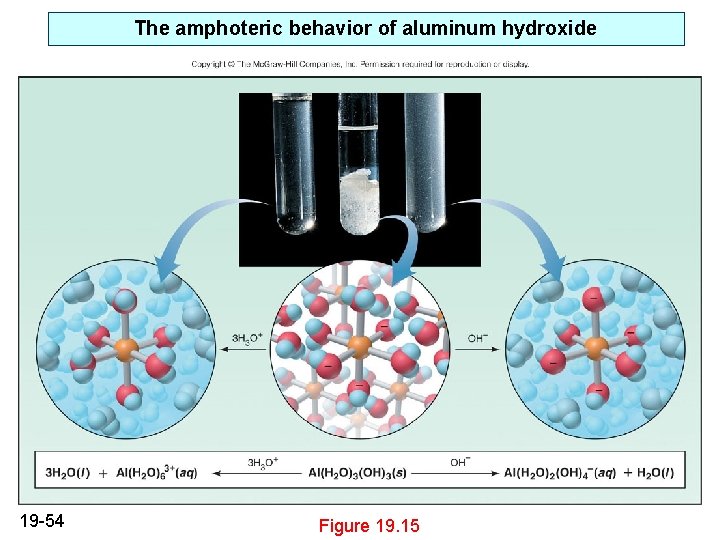
The amphoteric behavior of aluminum hydroxide 19 -54 Figure 19. 15

Selective Precipitation Selection of an ion in solution by precipitation; achieved by adding a precipitating agent (ion) to the solution until the Qsp of the more soluble compound is almost equal to its Ksp (but Qsp < Ksp). This ion remains in solution, whereas the other ion(s) having Qsp > Ksp precipitate. 19 -55

Sample Problem 19. 12 Separating ions by selective precipitation PROBLEM: A solution consists of 0. 20 M Mg. Cl 2 and 0. 10 M Cu. Cl 2. Calculate the [OH-] that would separate the metal ions as their hydroxides. Ksp of Mg(OH)2 = is 6. 3 x 10 -10; Ksp of Cu(OH)2 = 2. 2 x 10 -20. PLAN: Both precipitates have the same ion ratio, 1: 2, so we can compare their Ksp values to determine which has the greater solubility. Cu(OH)2 will precipitate first (it has the smaller Ksp) so we calculate the [OH-] needed for a saturated solution of Mg(OH)2. This will ensure that we do not precipitate Mg(OH)2. We can then check how much Cu 2+ remains in solution. SOLUTION: Mg(OH)2(s) Mg 2+(aq) + 2 OH-(aq) Ksp = 6. 3 x 10 -10 Cu(OH)2(s) Cu 2+(aq) + 2 OH-(aq) Ksp = 2. 2 x 10 -20 [OH-] needed for a saturated Mg(OH)2 solution = = 5. 6 x 10 -5 M 19 -56

Sample Problem 19. 12 (continued) Use the Ksp for Cu(OH)2 to find the amount of Cu 2+ remaining in solution. [Cu 2+] = Ksp/[OH-]2 = 2. 2 x 10 -20/(5. 6 x 10 -5)2 =7. 0 x 10 -12 M Since the solution was 0. 10 M Cu. Cl 2, virtually none of the Cu 2+ remains in solution. 19 -57

Qualitative Analysis Self-Study: pp. 841 -845 in textbook Only an overview of this material will be provided in class. You will be responsible, however, for this material for the Final Exam. 19 -58

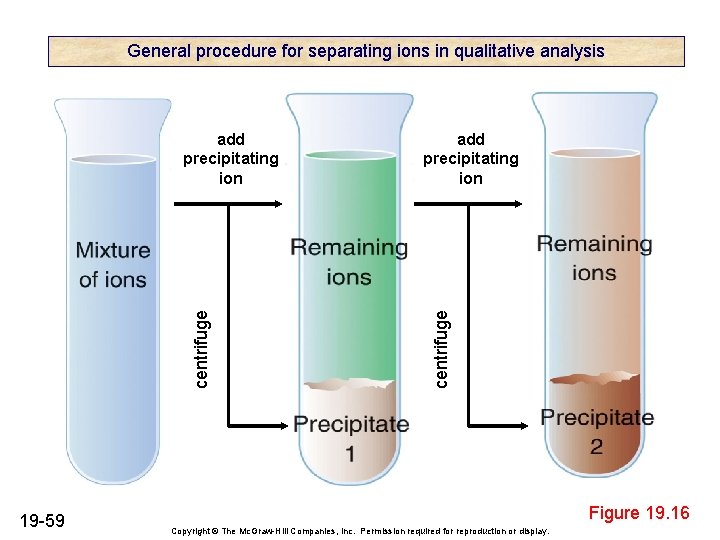
General procedure for separating ions in qualitative analysis 19 -59 add precipitating ion centrifuge add precipitating ion Figure 19. 16 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

A qualitative analysis scheme for separating cations into five ion groups Figure 19. 17 19 -60 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. add (NH 4)2 HPO 4 centrifuge add NH 3/NH 4+ buffer(p. H 8) centrifuge add 6 M HCl acidify to p. H 0. 5; add H 2 S

19 -61

Tests to determine the presence of cations in ion group 5 (a) flame test for Na+: yellow-orange (b) flame test for K+: violet (c) NH 4+ + OH- : p. H test for NH 3 gas Figure 19. 18 19 -62

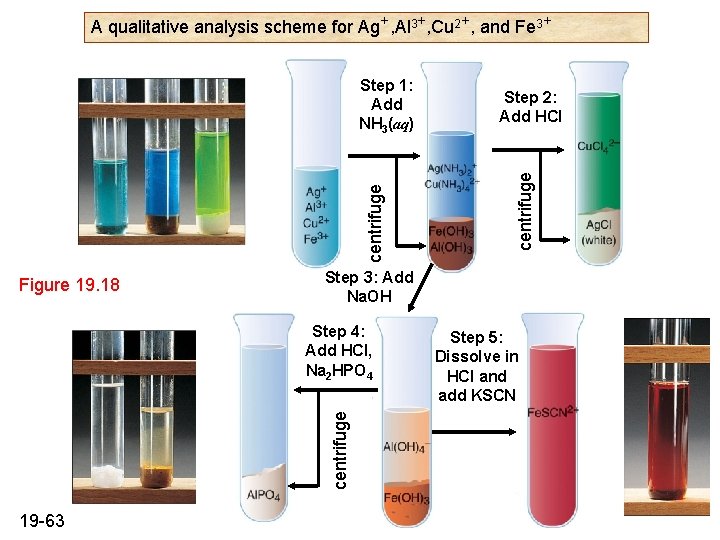
A qualitative analysis scheme for Ag+, Al 3+, Cu 2+, and Fe 3+ Figure 19. 18 Step 3: Add Na. OH centrifuge Step 4: Add HCl, Na 2 HPO 4 19 -63 Step 2: Add HCl centrifuge Step 1: Add NH 3(aq) Step 5: Dissolve in HCl and add KSCN

End of Assigned Material 19 -64

A view inside Carlsbad Caverns, New Mexico Figure B 19. 1 19 -65

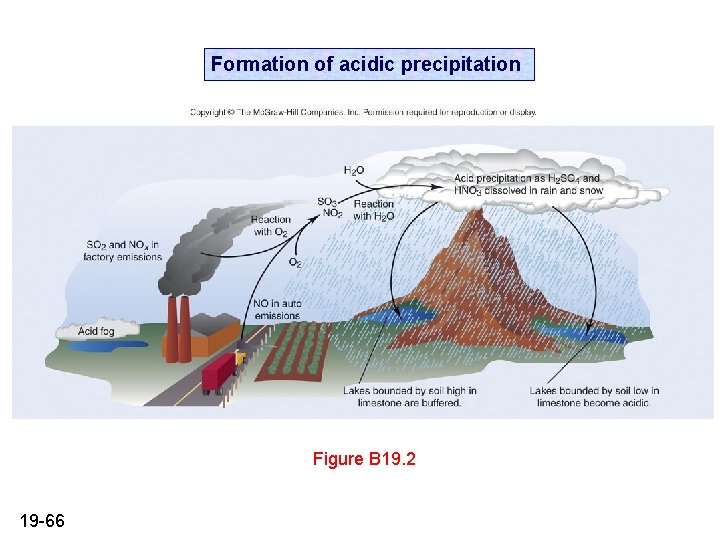
Formation of acidic precipitation Figure B 19. 2 19 -66

The effect of acid rain on statuary Location: New York City Figure B 19. 4 19 -67

A forest damaged by acid rain Figure B 19. 3 19 -68