Chapter 19 Fibonacci Heap Many of the slides

Chapter 19: Fibonacci Heap Many of the slides are from Prof. Leong Hon Wai’s resources at National University of Singapore

Priority Queue ADT q Priority Queue is an ADT for maintaining a set S of elements, each with a key value and supports the following operations: v INSERT(S, x) inserts element x into S (also write as S S {x} v MINIMUM(S) returns element in S with min key v EXTRACT-MIN(S) removes and returns element in S with min key v DECREASE-KEY(S, x, k) decreases the value of element x’s key to a new (smaller) value k.

PQ implementations… q Many data structures proposed for PQ 1964 Binary Heap J. Williams 1972 Leftist Heap C. A. Crane 1978 Binomial Heap J. Vuillemin 1984 Fibonacci Heap M. L. Fredman, R. E. Tarjan 1985 Skew Heap 1988 Relaxed Heap D. D. Sleator R. E. Tarjan Driscoll, Gabow Shrairman, Tarjan

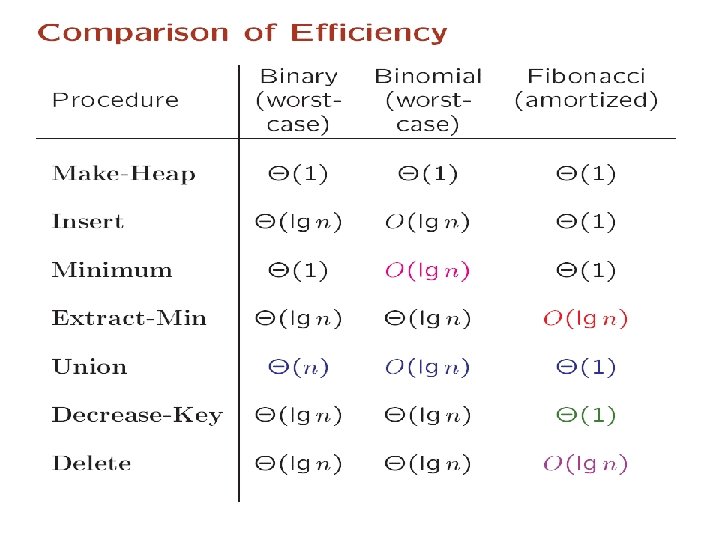
Different Priority Queues q Time Bounds for different PQ implementations v n is the number of items in the PQ Data Str INSERT MIN Extract -MIN D-KEY DELETE Union Binary H O(lg n) O(1) O(lg n) O(n) Binomial H O(lg n) O(lg n) O(1) Fibonacci

Binary Min-Heap (as in Heapsort) q Binary min-heap is an array A[1. . n] that can be viewed as a nearly complete binary tree q Number the nodes using level order traversal v LEFT(i) = 2 i and RIGHT(i) = 2 i+1 and v PARENT(i) = i/2 v Height of tree lg n q Heap Property: (Each node ≥ its parent node) v A[PARENT(i)] A[i]

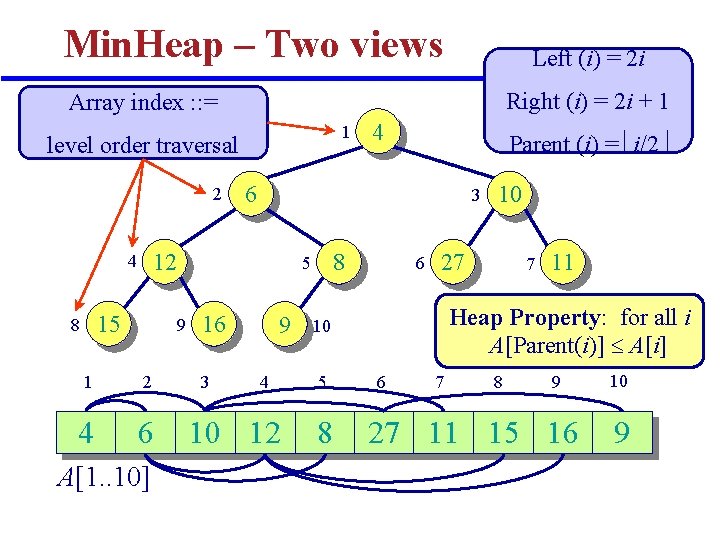
Min. Heap – Two views Left (i) = 2 i Right (i) = 2 i + 1 Array index : : = 1 level order traversal 2 15 8 3 1 2 4 6 A[1. . 10] 8 5 9 16 3 Parent (i) = i/2 6 12 4 4 9 4 10 12 6 27 8 7 11 Heap Property: for all i A[Parent(i)] A[i] 10 5 10 6 7 8 9 27 11 15 16 10 9

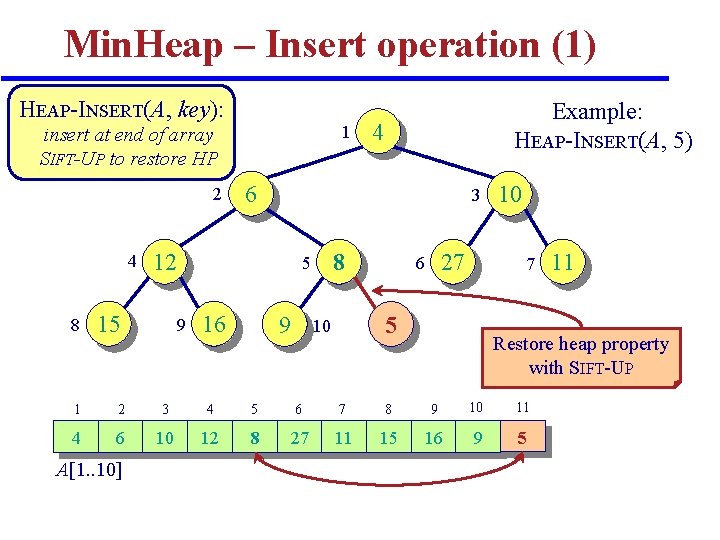
Min. Heap – Insert operation (1) HEAP-INSERT(A, key): 1 insert at end of array SIFT-UP to restore HP 2 4 8 3 8 5 9 4 6 12 15 Example: HEAP-INSERT(A, 5) 16 9 27 6 7 5 10 10 Restore heap property with SIFT-UP 1 2 3 4 5 6 7 8 9 10 11 4 6 10 12 8 27 11 15 16 9 5 A[1. . 10] 11

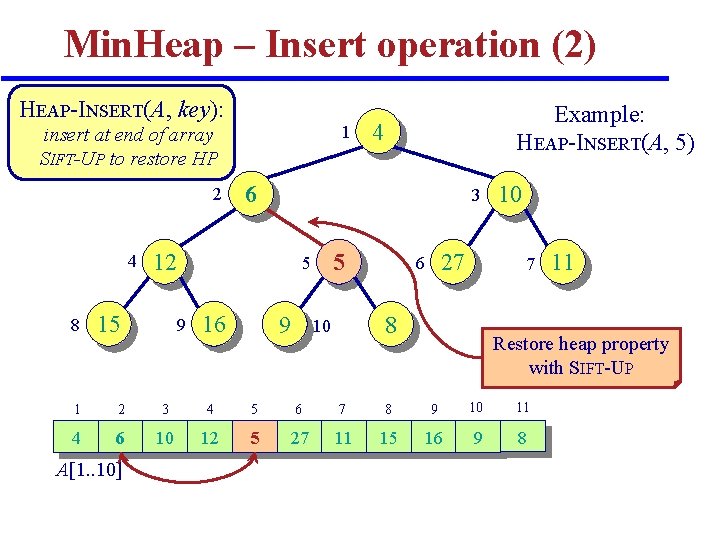
Min. Heap – Insert operation (2) HEAP-INSERT(A, key): 1 insert at end of array SIFT-UP to restore HP 2 4 8 3 5 5 9 4 6 12 15 Example: HEAP-INSERT(A, 5) 16 9 27 6 7 8 10 10 Restore heap property with SIFT-UP 1 2 3 4 5 6 7 8 9 10 11 4 6 10 12 5 27 11 15 16 9 8 A[1. . 10] 11

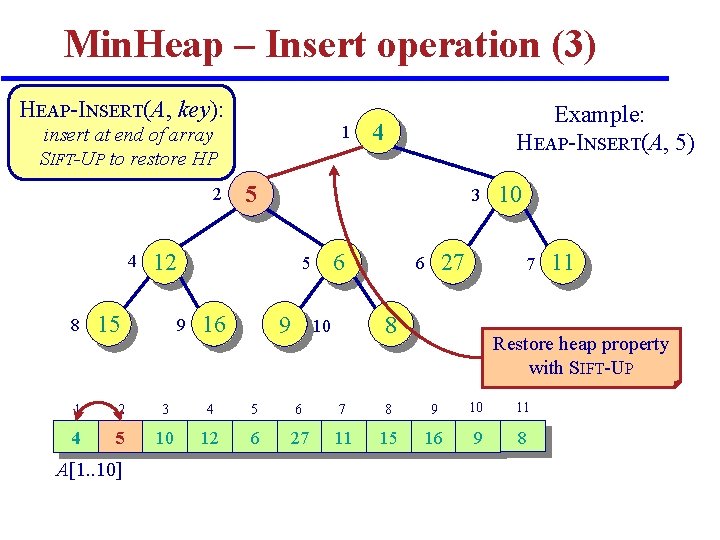
Min. Heap – Insert operation (3) HEAP-INSERT(A, key): 1 insert at end of array SIFT-UP to restore HP 2 4 8 3 6 5 9 4 5 12 15 Example: HEAP-INSERT(A, 5) 16 9 27 6 7 8 10 10 Restore heap property with SIFT-UP 1 2 3 4 5 6 7 8 9 10 11 4 5 10 12 6 27 11 15 16 9 8 A[1. . 10] 11

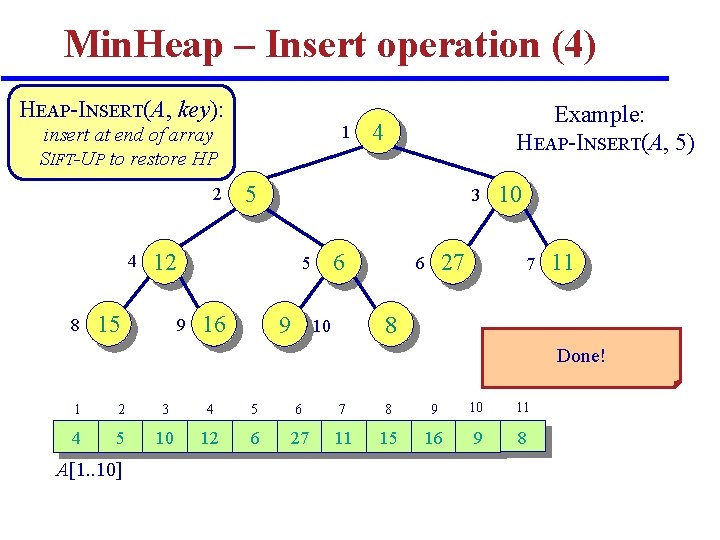
Min. Heap – Insert operation (4) HEAP-INSERT(A, key): 1 insert at end of array SIFT-UP to restore HP 2 4 8 3 6 5 9 4 5 12 15 Example: HEAP-INSERT(A, 5) 16 9 27 6 10 7 11 8 10 Done! 1 2 3 4 5 6 7 8 9 10 11 4 5 10 12 6 27 11 15 16 9 8 A[1. . 10]

Min. Heap – Insert operation (5) HEAP-INSERT(A, key) ⊳ A is a heap (array) heap-size(A) + 1 A[heap-size(A)] key SIFT-UP(A, heap-size(A)) THEAP-INSERT(n) = TSIFT-UP(n) + (1) SIFT-UP(A, n) = O(lg n) key A[n] i n while i > 1 and A[PARENT(i)] > key do A[i] A[PARENT(i)] i PARENT(i) A[i] key TSIFT-UP(n) = O(h) = O(lg n) (h comparisons, h data-moves)

Min. Heap – Extract-Min operation (1) HEAP-EXTRACT-MIN(A): 1 Exchange A[1] and A[n] SIFT-DOWN to restore HP 2 4 8 6 3 12 15 8 5 9 4 16 9 27 6 10 10 7 11 A[1] is is the minimum Exchange A[1] with A[n] 1 2 3 4 5 6 7 8 9 10 4 6 10 12 8 27 11 15 16 9 A[1. . 10]

Min. Heap – Extract-Min operation (2) HEAP-EXTRACT-MIN(A): 1 Exchange A[1] and A[n] SIFT-DOWN to restore HP 2 4 8 15 3 8 5 9 9 6 12 16 4 27 6 10 7 11 SIFT-DOWN to restore heap property 10 1 2 3 4 5 6 7 8 9 10 9 6 10 12 8 27 11 15 16 4 A[1. . 10] return min 4

Min. Heap – Extract-Min operation (3) HEAP-EXTRACT-MIN(A): 1 Exchange A[1] and A[n] SIFT-DOWN to restore HP 2 4 6 9 3 12 5 8 27 6 8 15 1 2 3 4 5 6 7 8 9 6 9 10 12 8 27 11 15 16 A[1. . 10] 9 16 10 7 11 SIFT-DOWN to restore heap property 10

Min. Heap – Extract-Min operation (4) HEAP-EXTRACT-MIN(A): 1 Exchange A[1] and A[n] SIFT-DOWN to restore HP 2 4 6 8 3 12 5 9 27 6 8 15 1 2 3 4 5 6 7 8 9 6 8 10 12 9 27 11 15 16 A[1. . 10] 9 10 7 16 11 Done! 10

Min. Heap – Extract-Min operation (5) HEAP-EXTRACT-MIN(A, key) ⊳ A is a heap (array) min A[1] A[heap-size(A)] heap-size(A) 1 SIFT-DOWN(A, 1) TSIFT-DOWN (n) = O(h) = O(lg n) (2 h comparisons, h data-moves) THEAP-EXTRACT-MIN (n) = O(lg n) SIFT-DOWN(A, i) while i is not a leaf do let j be the index of min child of i if A[i] > A[j] then exchange A[i] A[j] i j else i heap-size(A)+1 ⊳ make i a leaf

Min. Heap – Decrease-Key (1) HEAP-DECREASE-KEY(A, i, key): update the key of A[i] SIFT-UP to restore HP 2 4 8 3 8 5 9 4 6 12 15 1 HEAP-DECREASE-KEY(A, 9, 3) 16 9 27 6 7 10 1 2 3 4 5 6 7 8 9 10 4 6 10 12 8 27 11 15 16 9 A[1. . 10] 10 11

Min. Heap – Decrease-Key (2) HEAP-DECREASE-KEY(A, i, key): update the key of A[i] SIFT-UP to restore HP 2 4 8 3 8 5 9 4 6 12 15 1 HEAP-DECREASE-KEY(A, 9, 3) 3 9 27 6 7 10 11 Restore heap property with SIFT-UP 1 2 3 4 5 6 7 8 9 10 4 6 10 12 8 27 11 15 3 9 A[1. . 10] 10

Min. Heap – Decrease-Key (3) HEAP-DECREASE-KEY(A, i, key): update the key of A[i] SIFT-UP to restore HP 2 4 8 3 8 5 9 4 6 3 15 1 HEAP-DECREASE-KEY(A, 9, 3) 12 9 27 6 7 10 1 2 3 4 5 6 7 8 9 10 4 6 10 3 8 27 11 15 12 9 A[1. . 10] 10 11

Min. Heap – Decrease-Key (4) HEAP-DECREASE-KEY(A, i, key): update the key of A[i] SIFT-UP to restore HP 2 4 8 3 8 5 9 4 3 6 15 1 HEAP-DECREASE-KEY(A, 9, 3) 12 9 27 6 7 10 1 2 3 4 5 6 7 8 9 10 4 3 10 6 8 27 11 15 12 9 A[1. . 10] 10 11

Min. Heap – Decrease-Key (5) HEAP-DECREASE-KEY(A, i, key): update the key of A[i] SIFT-UP to restore HP 2 4 8 3 8 5 9 3 4 6 15 1 HEAP-DECREASE-KEY(A, 9, 3) 12 9 27 6 10 7 11 10 DONE ! 1 2 3 4 5 6 7 8 9 10 3 4 10 6 8 27 11 15 12 9 A[1. . 10]

Min. Heap – Insert operation (6) HEAP-DECREASE-KEY (A, i, key) ⊳ Update A[i] to key A[i] key SIFT-UP(A, i) TDECREASE-KEY(n) = TSIFT-UP(n) + (1) = O(lg n) (h comparisons, h data-moves)

Binary Heap (Summary) q HEAP-MINIMUM(A) O(1) q HEAP-INSERT(A, x) O(lg n) q HEAP-EXTRACT-MIN(A) O(lg n) q HEAP-DECREASE-KEY(A, i, k) O(lg n) v return root v append to end, sift-up v Replace root, sift-down v update key, sift-up q What about v HEAP-DELETE(A, i) v HEAP-MELD(A, B)

How about Union? q A mergeable heap is any data structure that supports the basic heap operation plus union q Union (H 1, H 2) creates and returns a new heap

Other Heaps

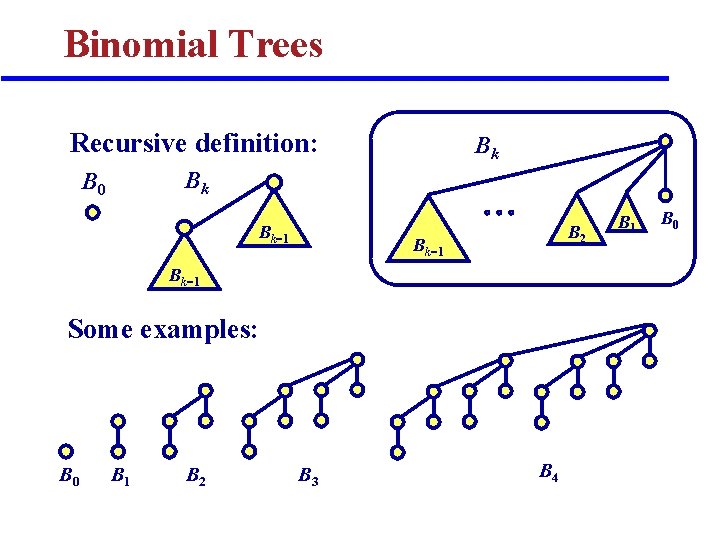
Binomial Trees Recursive definition: Bk Bk B 0 Bk 1 B 2 Bk 1 Some examples: B 0 B 1 B 2 B 3 B 4 B 1 B 0

Properties of Binomial Trees q For a Binomial Tree Bk (of order k) 1. 2. 3. 4. there are 2 k nodes, the height of the tree is k, root has degree k and deleting the root gives binomial trees B 0, B 1, …, Bk 1 depth Proof: (DIY, by induction) 0 1 2 3 B 0 B 1 B 2 B 3 B 4 4

Defining Property of Binomial Trees There are exactly nodes at depth i, (0 i k) depth B 4 Nodes 0 1 1 4 2 6 3 4 4 1

Binomial Heap (Vuillemin, 1978) q A sequence of binomial trees that satisfy v binomial heap property (each tree Bk is a min-heap) v 0 or 1 binomial tree Bk of order k, q There at most lg n + 1 binomial trees. q Eg: A binomial heap H with n = 11 nodes. head[H] 18 3 6 37 48 11 = (1011)2 29 10 31 17 50 B 1 B 3 44

Representing Binomial Heaps (1) q Each node x stores v v v key[x] degree[x] p[x] child[x] sibling[x] parent key 10 1 degree sibling q (3 pointers per node) child

Representing Binomial Heap (2) head[H] 6 3 18 37 48 29 10 31 17 44 50 head[H] 18 0 Each node x has p[x] child[x] sibling[x] degree[x], key[x] 3 1 37 0 48 1 50 2 29 2 10 1 31 0 17 0 6 3 44 0

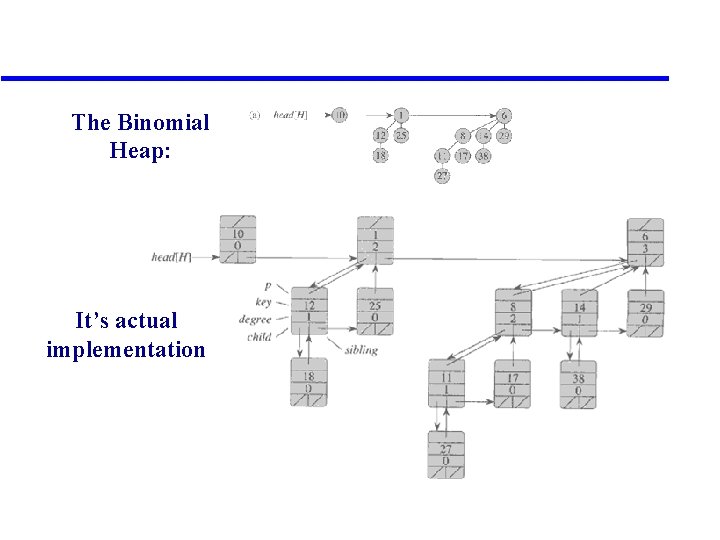
The Binomial Heap: It’s actual implementation

Operations on a Binomial Heap q MAKE-BINOMIAL-HEAP(H) v Allocate object H, make head[H] = NIL. (1). q BINOMIAL-HEAP-MINIMUM(H) v Search the root list for minimum. O(lg n). head[H] 18 3 6 37 48 29 10 31 17 50 B 1 B 3 44

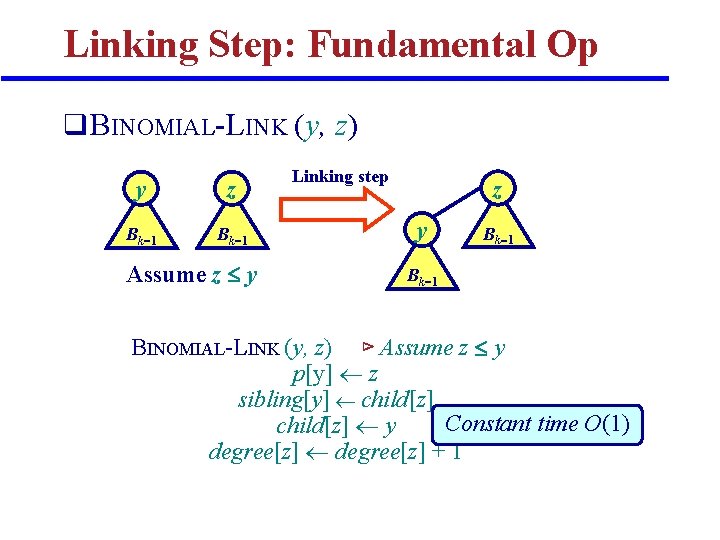
Linking Step: Fundamental Op q BINOMIAL-LINK (y, z) y z Bk 1 Assume z y Linking step z y Bk 1 BINOMIAL-LINK (y, z) ⊳ Assume z y p[y] z sibling[y] child[z] Constant time O(1) child[z] y degree[z] + 1

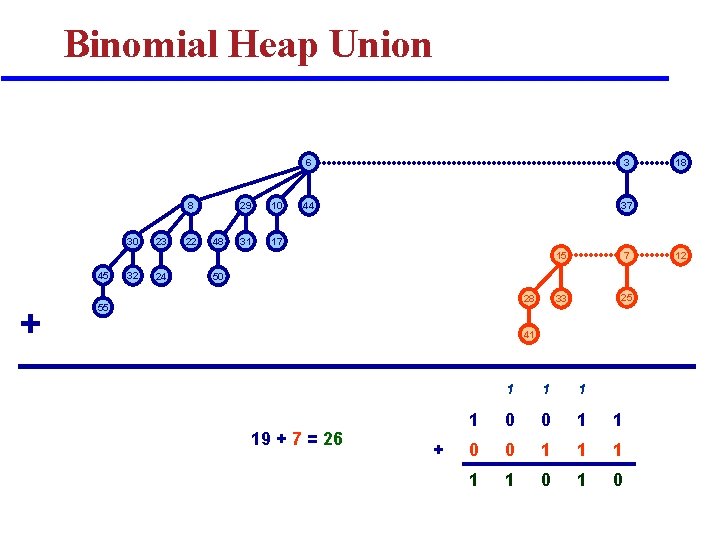
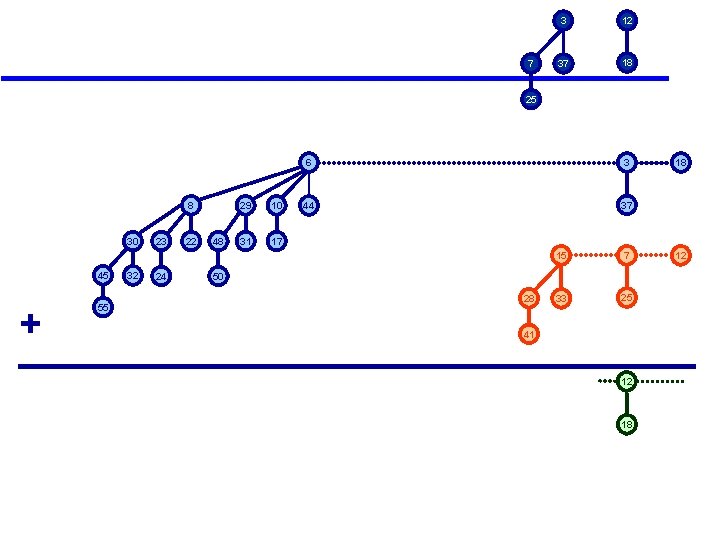
Binomial Heap Union 8 30 45 + 32 23 24 22 48 29 10 31 17 6 3 44 37 15 7 33 25 50 28 55 41 19 + 7 = 26 + 1 1 0 0 1 1 1 1 1 0 18 12

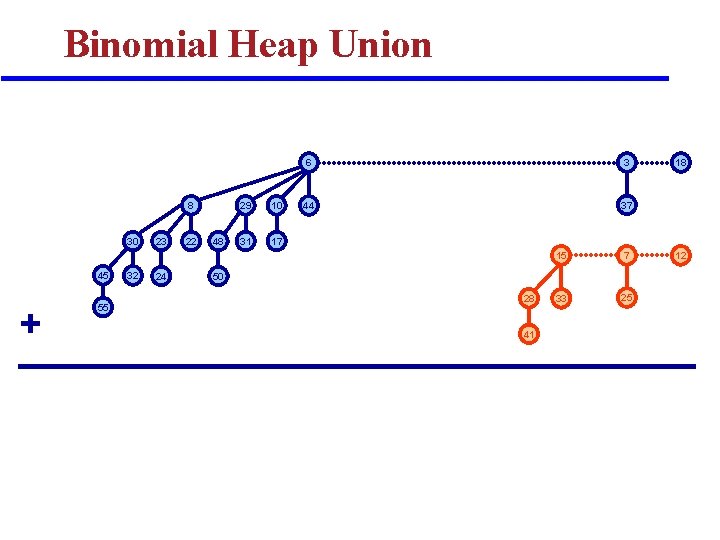
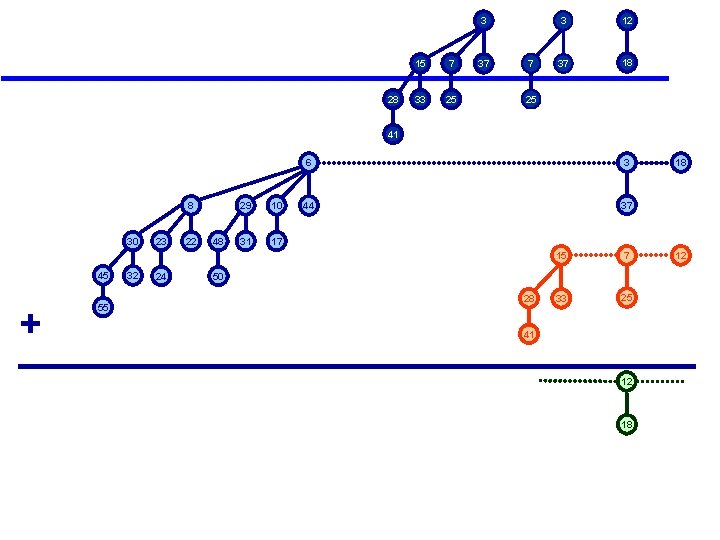
Binomial Heap Union 8 30 45 + 55 32 23 24 22 48 29 10 31 17 6 3 44 37 15 7 33 25 50 28 41 18 12

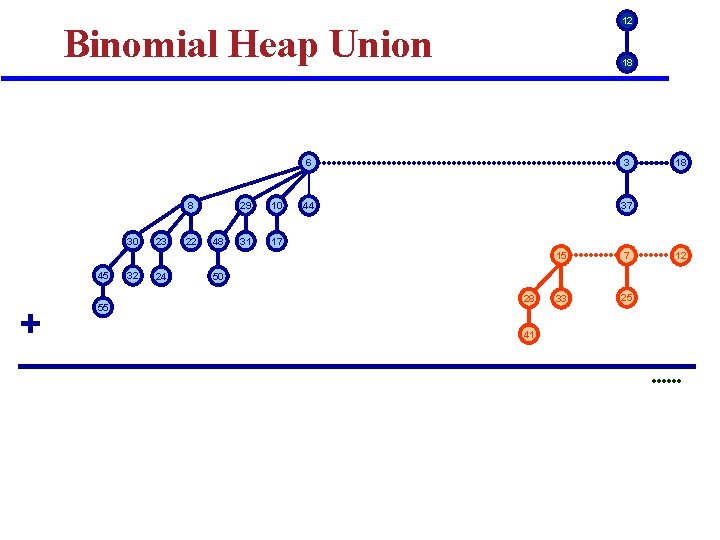
12 Binomial Heap Union 8 30 45 + 55 32 23 24 22 48 29 10 31 17 18 6 3 44 37 15 7 33 25 50 28 41 18 12

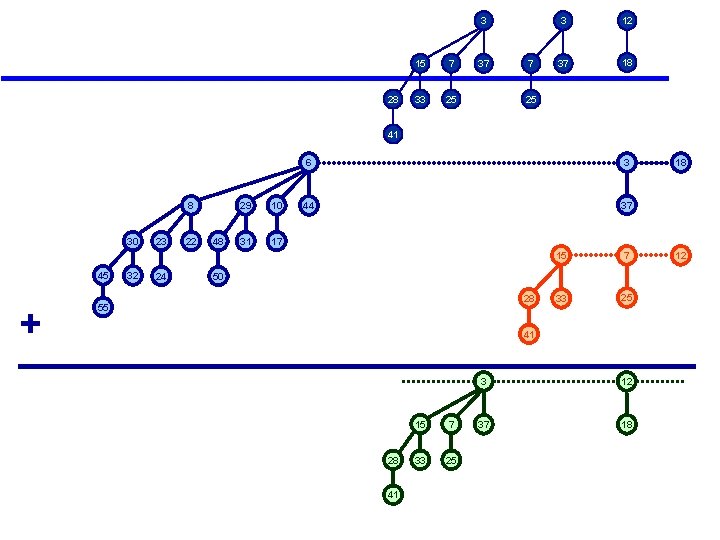
7 3 12 37 18 25 8 30 45 + 55 32 23 24 22 48 29 10 31 17 6 3 44 37 15 7 33 25 50 28 41 12 18 18 12

3 28 15 7 33 25 37 7 3 12 37 18 25 41 8 30 45 + 55 32 23 24 22 48 29 10 31 17 6 3 44 37 15 7 33 25 50 28 41 12 18 18 12

3 28 15 7 33 25 37 7 3 12 37 18 25 41 8 30 45 + 32 23 24 22 48 29 10 31 17 6 3 44 37 15 7 33 25 50 28 55 41 28 41 15 7 33 25 3 12 37 18 18 12

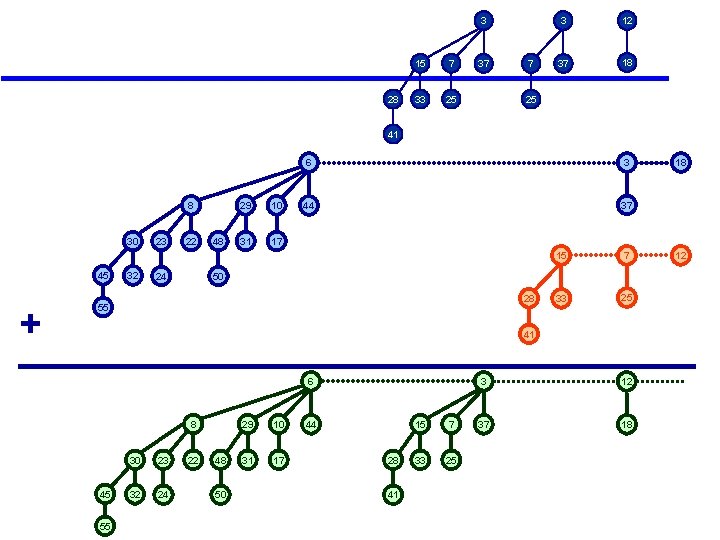
3 28 15 7 33 25 37 7 3 12 37 18 25 41 8 30 45 + 32 23 22 24 48 29 10 31 17 6 3 44 37 15 7 33 25 50 28 55 41 6 8 45 55 30 23 32 24 22 48 50 29 10 31 17 44 28 41 15 7 33 25 3 12 37 18 18 12

Binomial Heap Union q MAKE-BINOMIAL-HEAP-UNION (H 1, H 2) : v Create a heap H that is the union of two heaps H 1 and H 2 v Analogous to binary addition of n 1 and n 2 q Running time. : O(log n) [n = n 1 + n 2] v Prop to # of trees in root lists 2( log 2 n + 1). 19 + 7 = 26 + 1 1 0 0 1 1 1 1 1 0

More Operations (1) q BINOMIAL-HEAP-INSERT(H, x) v Create a one-item (x) binomial heap H 1 and then union H and H 1. O(lg n). q BINOMIAL-HEAP-EXTRACT-MIN(H) v Find minimum, remove root, then union. O(lg n). head[H] 18 3 6 37 48 29 10 31 17 50 B 1 B 3 44

More Operations (2) q BINOMIAL-HEAP-DECREASE (H, x, k) q BINOMIAL-HEAP-DELETE (H, x) head[H] 18 3 6 37 48 29 10 31 17 50 B 1 B 3 44

Binomial Heaps (Summary) q MINIMUM(H) O(lg n) q UNION(H 1, H 2) O(lg n) q INSERT(H, x) O(lg n) q EXTRACT-MIN(H) O(lg n) q DECREASE-KEY (H, x, k) O(lg n) q DELETE (H, x) O(lg n)

Binomial Fibonacci Heaps q Key advantages of Binomial Heap v Elegant and fast – O(lg n) v But, it takes O(lg n) to “maintain” the elegant structure all the time. q Fibonacci Heaps v Want fast INSERT, DECREASE-KEY v Be lazy… u Do as little as possible, until there is no choice. v Relax the structure slightly

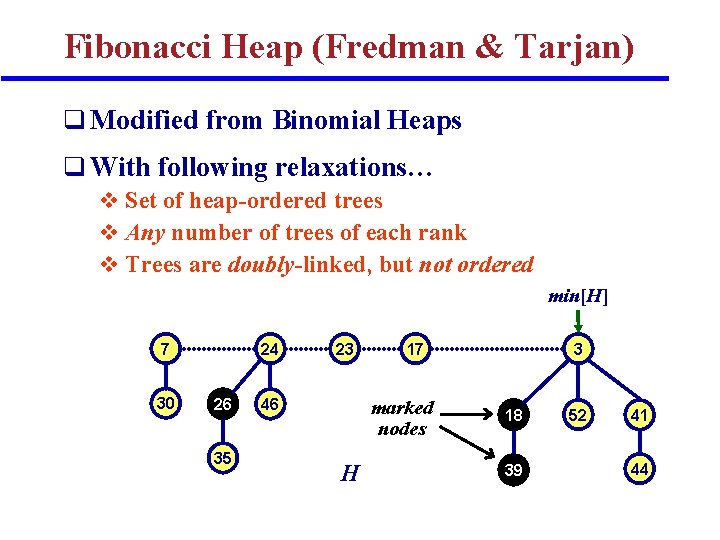
Fibonacci Heap (Fredman & Tarjan) q Modified from Binomial Heaps q With following relaxations… v Set of heap-ordered trees v Any number of trees of each rank v Trees are doubly-linked, but not ordered min[H] 7 30 24 26 35 23 46 17 marked nodes H 3 18 39 52 41 44

Representing Fibonacci Heaps (1) q Each node x stores v v v v key[x] degree[x] (also rank(x)) mark[x] p[x] child[x] key, degree left[x] left right [x] (4 pointers per node) parent 10 1 FALSE mark right child

Representing Fibonacci Heaps (2) min[H] 7 30 24 26 23 17 46 3 18 35 52 41 44 39 min[H] 7 30 24 26 35 23 46 17 3 18 H 39 52 41 44

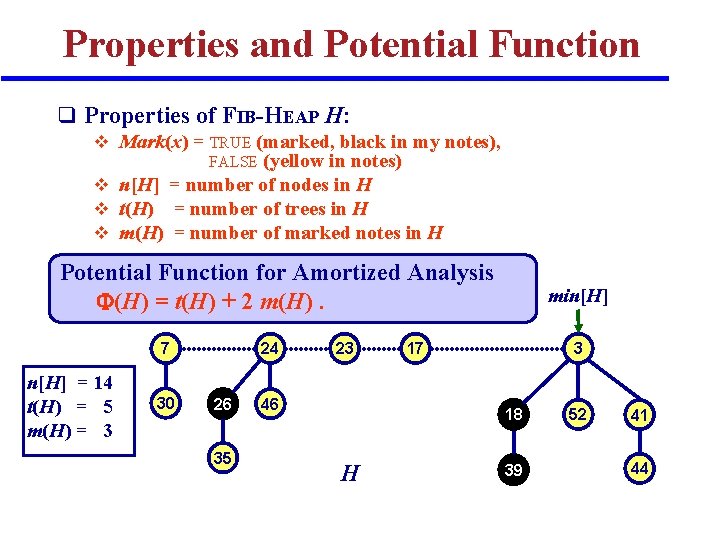
Properties and Potential Function q Properties of FIB-HEAP H: v Mark(x) = TRUE (marked, black in my notes), (yellow in notes) v n[H] = number of nodes in H v t(H) = number of trees in H v m(H) = number of marked notes in H FALSE Potential Function for Amortized Analysis (H) = t(H) + 2 m(H). 7 n[H] = 14 t(H) = 5 m(H) = 3 30 24 26 35 23 46 min[H] 17 3 18 H 39 52 41 44

Operations on a Fibonacci Heap q MAKE-FIB-HEAP(H) v Allocate object H, make min[H] = NIL. (1). q FIB-HEAP-MINIMUM(H) v min[H] points to minimum element. O(1). min[H] 7 n[H] = 14 t(H) = 5 m(H) = 3 30 24 26 35 23 46 17 3 18 H 39 52 41 44

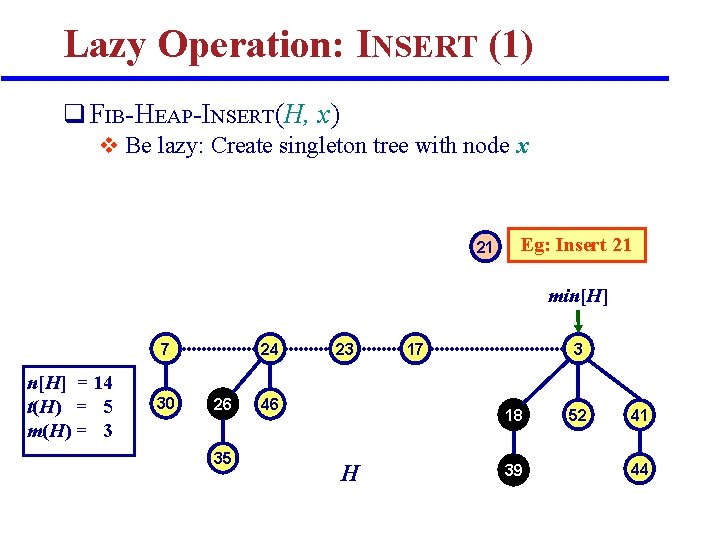
Lazy Operation: INSERT (1) q FIB-HEAP-INSERT(H, x) v Be lazy: Create singleton tree with node x 21 Eg: Insert 21 min[H] 7 n[H] = 14 t(H) = 5 m(H) = 3 30 24 26 35 23 46 17 3 18 H 39 52 41 44

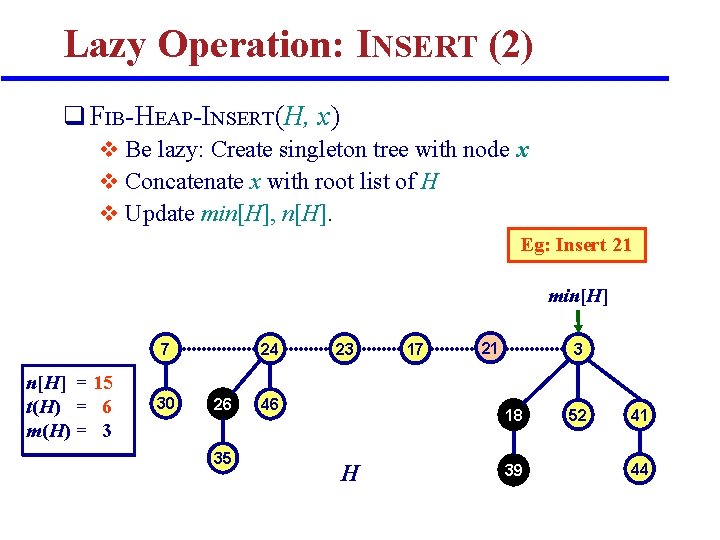
Lazy Operation: INSERT (2) q FIB-HEAP-INSERT(H, x) v Be lazy: Create singleton tree with node x v Concatenate x with root list of H v Update min[H], n[H]. Eg: Insert 21 min[H] 7 n[H] = 15 14 t(H) = 65 m(H) = 3 30 24 26 35 23 46 17 21 3 18 H 39 52 41 44

Pseudocode for INSERT FIB-HEAP-INSERT (H, x) O(1) Worst case time = O(1) Amortized time = O(1) degree[x] 0 p[x] NIL child[x] NIL left[x] x right[x] x mark[x] FALSE concatenate the root list containing x with root list H if min[H] = NIL or key[x] < key[min[H]] then min[H] x n[H] + 1 Amortized Time of INSERT: c’(H) = c(H) + (H’) (H) = O(1) + 1 = O(1)

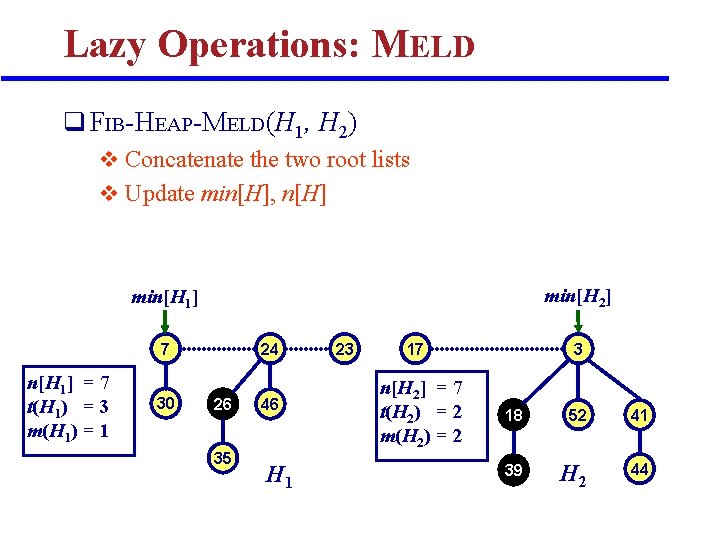
Lazy Operations: MELD q FIB-HEAP-MELD(H 1, H 2) v Concatenate the two root lists v Update min[H], n[H] min[H 2] min[H 1] 7 n[H 1] = 7 t(H 1) = 3 m(H 1) = 1 30 24 26 35 46 H 1 23 17 n[H 2] = 7 t(H 2) = 2 m(H 2) = 2 3 18 52 41 39 H 2 44

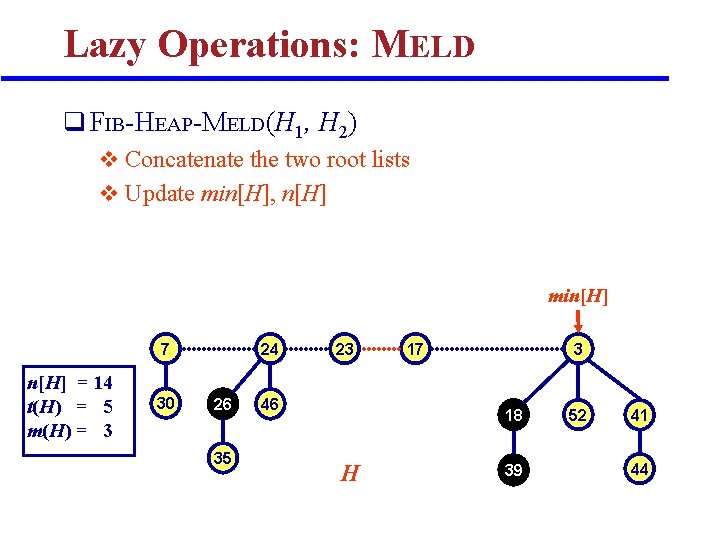
Lazy Operations: MELD q FIB-HEAP-MELD(H 1, H 2) v Concatenate the two root lists v Update min[H], n[H] min[H] 7 n[H] = 14 t(H) = 5 m(H) = 3 30 24 26 35 23 46 17 3 18 H 39 52 41 44

What have we got now? With lazy INSERT and MELD, We have a doubly-linked list, with pointer to minimum… ( So, when do we need to do real work? )

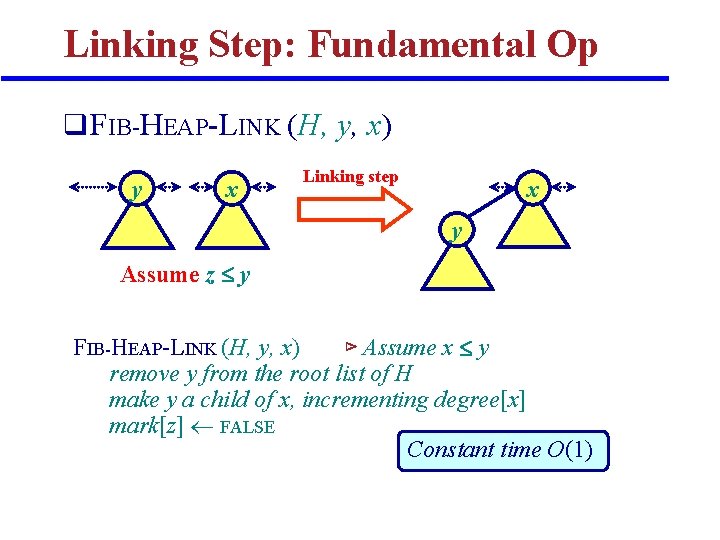
Linking Step: Fundamental Op q FIB-HEAP-LINK (H, y, x) y x Linking step x y Assume z y FIB-HEAP-LINK (H, y, x) ⊳ Assume x y remove y from the root list of H make y a child of x, incrementing degree[x] mark[z] FALSE Constant time O(1)

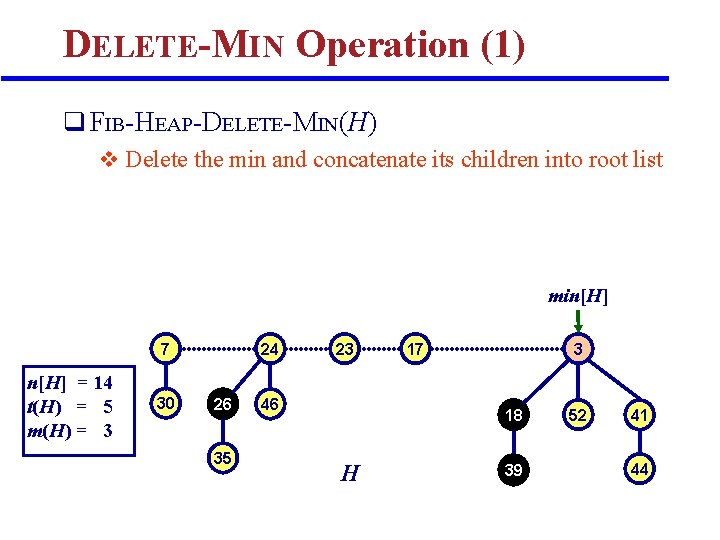
DELETE-MIN Operation (1) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list min[H] 7 n[H] = 14 t(H) = 5 m(H) = 3 30 24 26 35 23 46 17 3 18 H 39 52 41 44

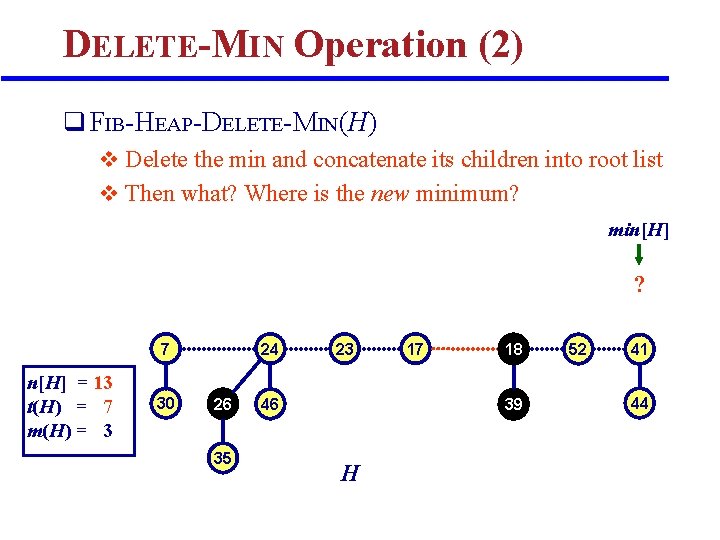
DELETE-MIN Operation (2) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Then what? Where is the new minimum? min[H] ? 7 n[H] = 13 t(H) = 7 m(H) = 3 30 24 26 35 23 46 17 18 39 H 52 41 44

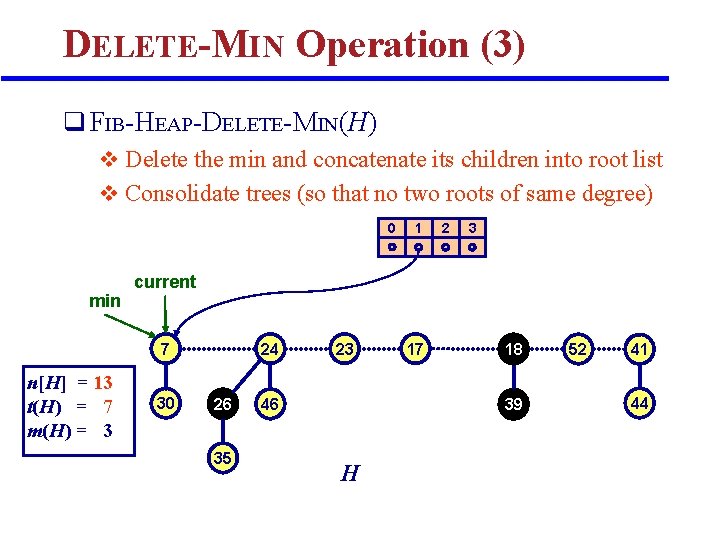
DELETE-MIN Operation (3) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 min 2 3 current 7 n[H] = 13 t(H) = 7 m(H) = 3 1 30 24 26 35 23 46 17 18 39 H 52 41 44

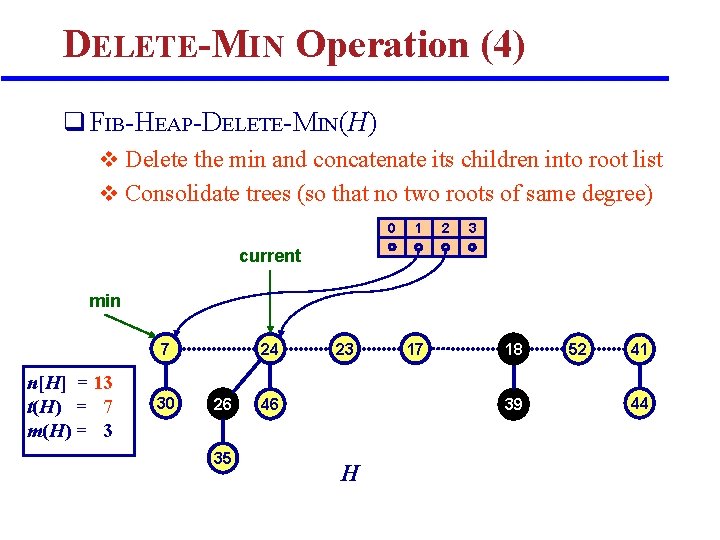
DELETE-MIN Operation (4) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 2 3 current min 7 n[H] = 13 t(H) = 7 m(H) = 3 30 24 26 35 23 46 17 18 39 H 52 41 44

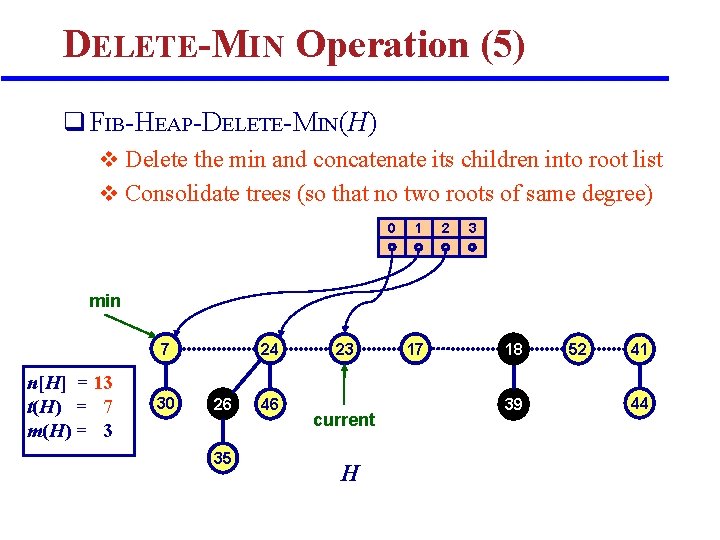
DELETE-MIN Operation (5) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 2 3 min 7 n[H] = 13 t(H) = 7 m(H) = 3 30 24 26 35 46 23 current H 17 18 39 52 41 44

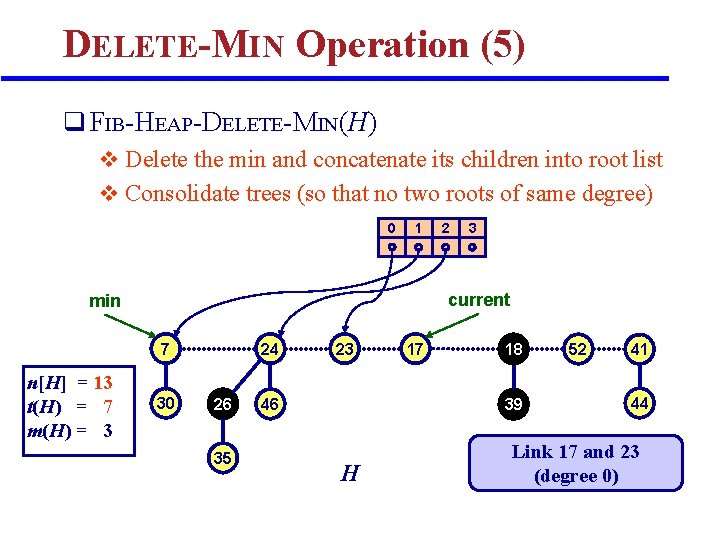
DELETE-MIN Operation (5) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 3 current min 7 n[H] = 13 t(H) = 7 m(H) = 3 2 30 24 26 35 23 46 17 18 39 H 52 41 44 Link 17 and 23 (degree 0)

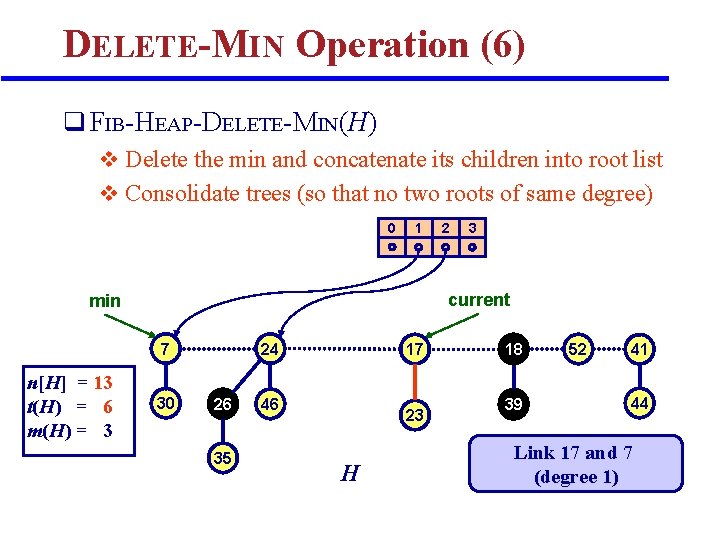
DELETE-MIN Operation (6) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 3 current min 7 n[H] = 13 t(H) = 6 m(H) = 3 2 30 24 26 35 17 46 23 H 18 39 52 41 44 Link 17 and 7 (degree 1)

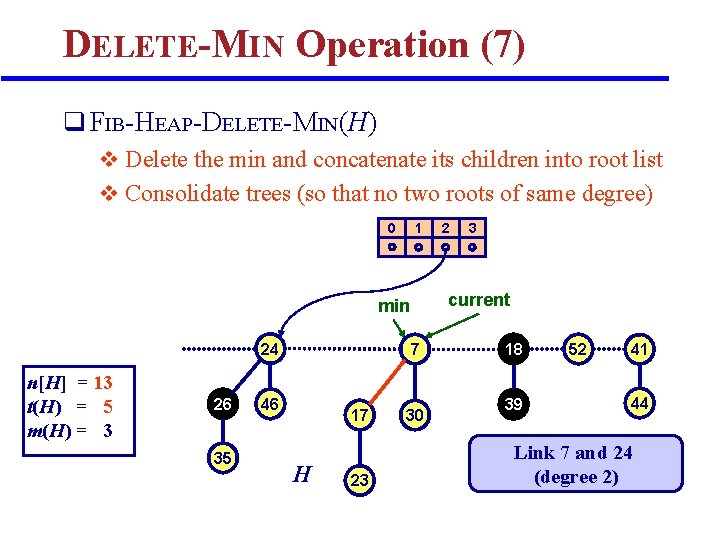
DELETE-MIN Operation (7) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 n[H] = 13 t(H) = 5 m(H) = 3 26 35 7 46 17 H 23 3 current min 24 2 30 18 39 52 41 44 Link 7 and 24 (degree 2)

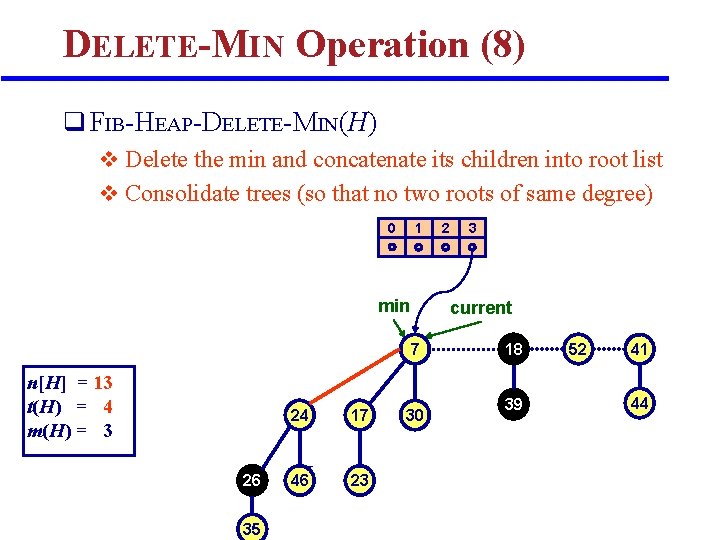
DELETE-MIN Operation (8) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 min 26 35 24 17 H 46 23 3 current 7 n[H] = 13 t(H) = 4 m(H) = 3 2 30 18 39 52 41 44

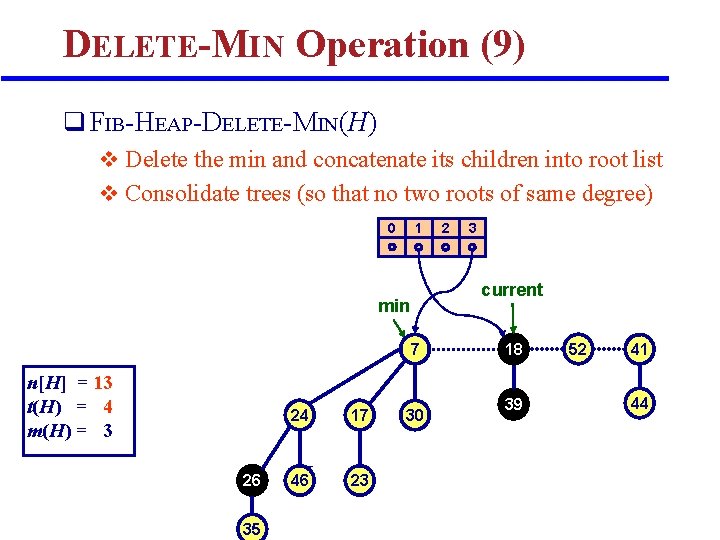
DELETE-MIN Operation (9) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 7 26 35 24 17 H 46 23 3 current min n[H] = 13 t(H) = 4 m(H) = 3 2 30 18 39 52 41 44

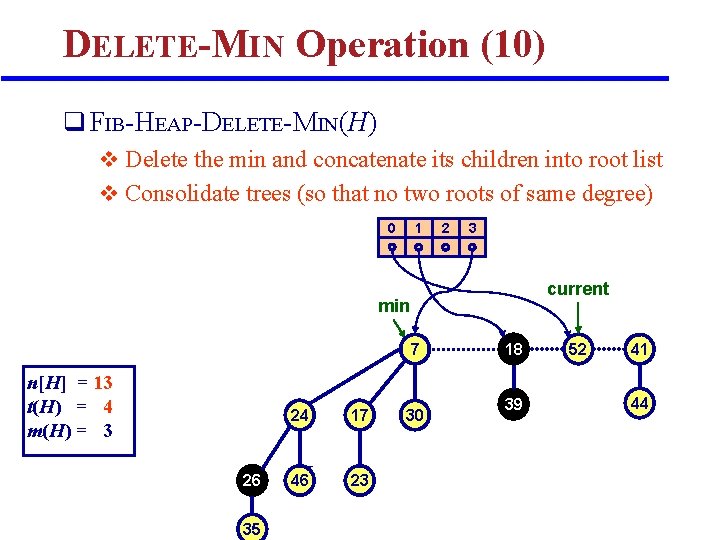
DELETE-MIN Operation (10) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 2 3 current min 7 n[H] = 13 t(H) = 4 m(H) = 3 26 35 24 17 H 46 23 30 18 39 52 41 44

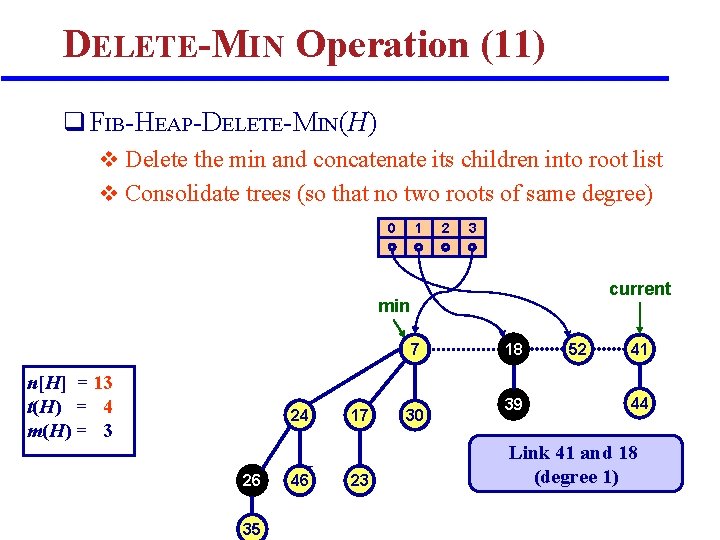
DELETE-MIN Operation (11) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 2 3 current min 7 n[H] = 13 t(H) = 4 m(H) = 3 24 26 35 H 46 17 23 30 18 39 52 41 44 Link 41 and 18 (degree 1)

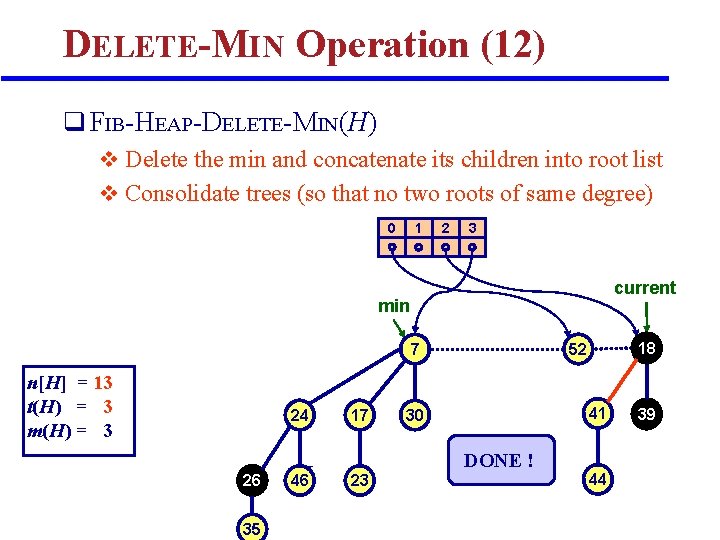
DELETE-MIN Operation (12) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) 0 1 2 3 current min n[H] = 13 t(H) = 3 m(H) = 3 24 26 35 H 46 17 41 30 DONE ! 23 18 52 7 44 39

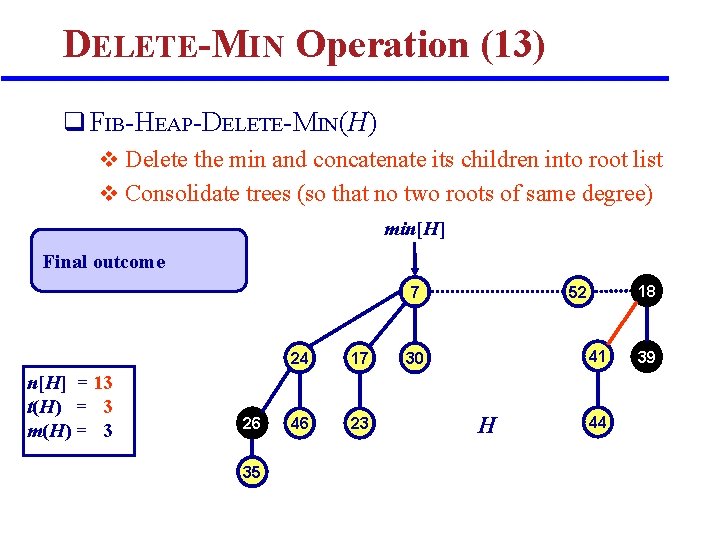
DELETE-MIN Operation (13) q FIB-HEAP-DELETE-MIN(H) v Delete the min and concatenate its children into root list v Consolidate trees (so that no two roots of same degree) min[H] Final outcome n[H] = 13 t(H) = 3 m(H) = 3 26 35 24 17 46 23 18 52 7 41 30 H 44 39

Analysis of DELETE-MIN q Notations: v Let H be the heap before DELETE-MIN op; v t(H) is number of trees in H; D(n) is max degree in any n-node FH v k linking steps are done during consolidation q Steps in DELETE-MIN v v v Remove min node x Concat children of x to root list Initialize ptr data structure A Consolidation step… TOTAL: # trees Cost O(1) O(D(n)) O(D(n)+k) Amortized Time: c’(H) = c(H) + = O(D(n)) t(H)+D(n) 1 k = D(n) 1 k Show later that D(n) = O(lg n)

What have we got now? (2) With Mergeable Heap Operations, i. e. , INSERT and MELD, DELETE-MIN can show that all the tree in H are actually Binomial Trees ! ( Now, how about DECREASE-KEY? )

DECREASE-KEY Operation (1 -1) q FIB-HEAP-DECREASE-KEY(H, x, k) [1 st example: case 1] v Decrease key of x to k v Cut off x from its parent, min[H] 7 n[H] = 16 t(H) = 3 m(H) = 3 35 24 17 26 46 45 30 88 72 23 21 18 38 39 41 52 Decrease 45 to 16

DECREASE-KEY Operation (1 -2) q FIB-HEAP-DECREASE-KEY(H, x, k) [1 st example: case 1] v Decrease key of x to k v Cut off x from its parent, insert x into root list, update min[H] 7 n[H] = 16 t(H) = 3 m(H) = 3 35 24 17 26 46 16 30 88 72 23 21 18 38 39 41 52 Decrease 45 to 16

DECREASE-KEY Operation (1 -3) q FIB-HEAP-DECREASE-KEY(H, x, k) [1 st example: case 1] v Decrease key of x to k v Cut off x from its parent, insert x into root list, update min[H] v If p[x] is not marked, mark p[x] min[H] 7 46 16 72 Mark p[x] n[H] = 16 t(H) = 4 m(H) = 43 24 26 30 Done ! 35 88 17 23 21 18 38 39 41 52 Decrease 45 to 16

DECREASE-KEY Operation (2 -1) q FIB-HEAP-DECREASE-KEY(H, x, k) [2 nd example: case 2] v Decrease key of x to k v Cut off x from its parent, insert x into root list, update min[H] 7 46 16 24 72 n[H] = 16 t(H) = 4 m(H) = 4 26 35 88 17 30 23 21 18 38 39 41 52 Decrease 35 to 4

DECREASE-KEY Operation (2 -2) q FIB-HEAP-DECREASE-KEY(H, x, k) [2 nd example: case 2] v Decrease key of x to k v Cut off x from its parent, insert x into root list, update min[H] v If p[x] is marked, then cut off p[x], unmark, insert… min[H] 46 16 72 n[H] = 16 t(H) = 5 m(H) = 4 4 7 p[x] is marked 26 88 24 17 30 23 21 18 38 39 41 52 Decrease 35 to 4

DECREASE-KEY Operation (2 -3) q FIB-HEAP-DECREASE-KEY(H, x, k) [2 nd example: case 2] v Decrease key of x to k v Cut off x from its parent, insert x into root list, update min[H] v If p[x] is marked, then cut off p[x], unmark, insert… REPEAT min[H] 46 16 72 n[H] = 16 t(H) = 6 m(H) = 3 4 26 88 7 24 p[p[x]] is marked 17 30 23 21 18 38 39 41 52 Decrease 35 to 4

DECREASE-KEY Operation (2 -4) q FIB-HEAP-DECREASE-KEY(H, x, k) [2 nd example: case 2] v Decrease key of x to k v Cut off x from its parent, insert x into root list, update min[H] v If p[x] is marked, then cut off p[x], unmark, insert… REPEAT min[H] 46 16 72 n[H] = 16 t(H) = 7 m(H) = 2 4 26 24 88 7 17 30 23 21 18 38 39 41 52 Done ! Decrease 35 to 4

Analysis of DECREASE-KEY q Notations: v Let H be the heap before DECREASE-KEY op; v t(H) is number of trees in H; m(H) is # marked nodes in H v c cascading cuts are done in total q Steps in DECREASE-KEY v v Decrease key of x Cascading cuts (unmark) Mark final parent node TOTAL: Amortized Time: c’(H) = c(H) + = O(1) Cost # trees O(1) O(c) t(H)+c # mark m(H) c+1 m(H) c+2 = c + 2(2 c) = (4 c ) Viola !!

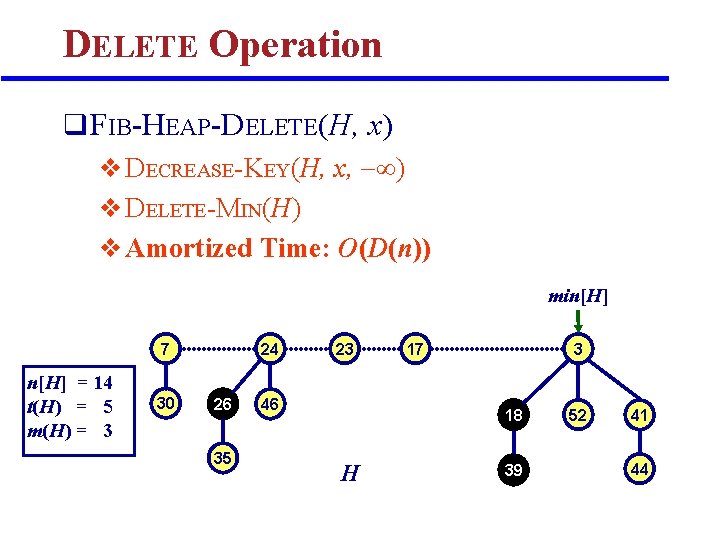
DELETE Operation q FIB-HEAP-DELETE(H, x) v DECREASE-KEY(H, x, ) v DELETE-MIN(H) v Amortized Time: O(D(n)) min[H] 7 n[H] = 14 t(H) = 5 m(H) = 3 30 24 26 35 23 46 17 3 18 H 39 52 41 44

Bounding the Maximum Degree D(n) : : = maximum degree in any FIB-HEAP with n nodes Shall prove that D(n) lg n = O(lg n) where = (1+ 5)/2 = 1. 61803 [golden ratio] and lg n = 1. 44 lg n

Bounding D(n) (1) Lemma 1: Let x be any node in FIB-HEAP with degree[x] = k. Let y 1, y 2, …, yn be children of x in the order in which they are linked to x (from earliest to latest). Then x degree[y 1] 0 and degree[yi] i 2 for i=2, … , k. … yk … yi y 2 y 1 Proof: When yi was linked to x, degree[x] = i 1 since all of y 1, y 2, …, yi 1 were already children of x. Thus, degree[yi] = degree[x] = i 1 at the time of linking. In addition, yi could lose at most 1 child, so degree[yi] i 2

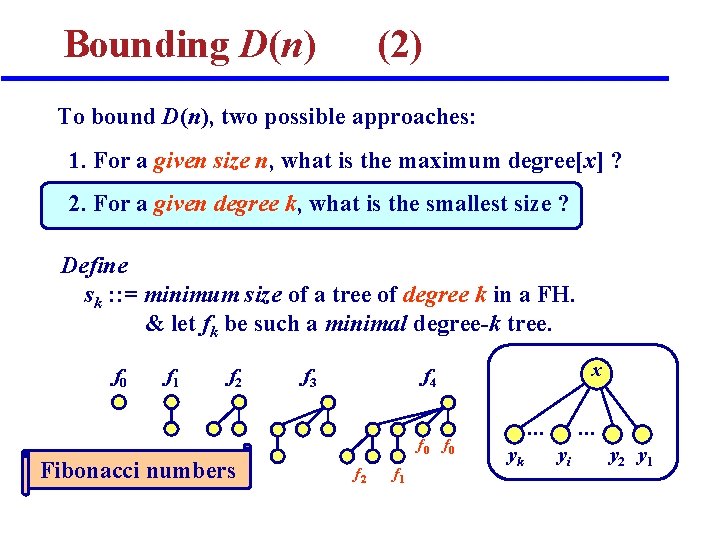
Bounding D(n) (2) To bound D(n), two possible approaches: 1. For a given size n, what is the maximum degree[x] ? 2. For a given degree k, what is the smallest size ? Define sk : : = minimum size of a tree of degree k in a FH. & let fk be such a minimal degree-k tree. f 0 f 1 f 2 f 3 f 0 Fibonacci numbers x f 4 f 2 f 1 … yk … yi y 2 y 1

Bounding D(n) (3) Lemma: Let x be node in FH, and degree[x]=k. Then, size(x) sk Fk+2 k. Proof: First some small values: s 0 = 1, s 1 = 2, s 2 = 3 General Case: x … yk … yi y 2 y 1 f 0 f 1 f 2 Then show: Fk+2 = 1 + (F 0+F 1+…+Fk) Fk+2 k sk Fk+2 Corollary: D(n) lg n = 1. 44 lg n = O(lg n)

Fibonacci Heaps (Summary) q MINIMUM(H) O(1) q UNION(H 1, H 2) O(1) q INSERT(H, x) O(1) q EXTRACT-MIN(H) O(lg n)* q DECREASE-KEY (H, x, k) O(1)* q DELETE (H, x) O(lg n)*