Chapter 19 Binary Trees Java Programming Program Design

Chapter 19: Binary Trees Java Programming: Program Design Including Data Structures

Chapter Objectives s s Learn about binary trees Explore various binary tree traversal algorithms Learn how to organize data in a binary search tree Discover how to insert and delete items in a binary search tree Java Programming: Program Design Including Data Structures 2

Binary Trees s A binary tree, T, is either empty or s T has a special node called the root node s T has two sets of nodes, LT and RT, called the left subtree and right subtree s LT and RT are binary trees s A binary tree can be shown pictorially Java Programming: Program Design Including Data Structures 3

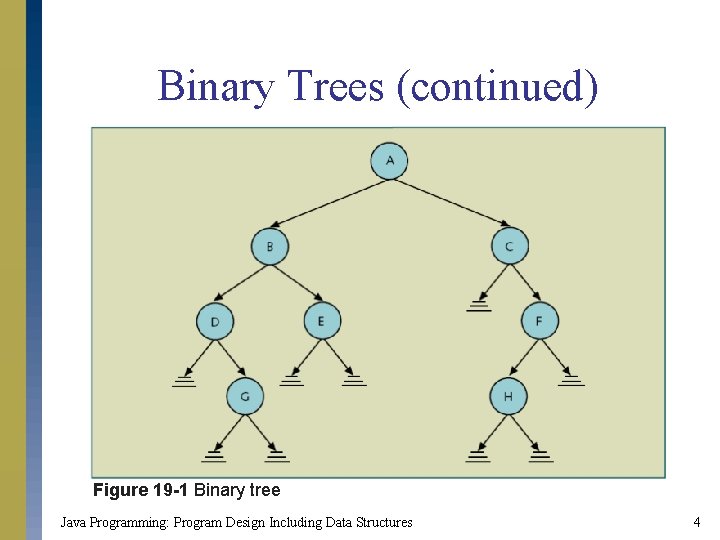
Binary Trees (continued) Figure 19 -1 Binary tree Java Programming: Program Design Including Data Structures 4

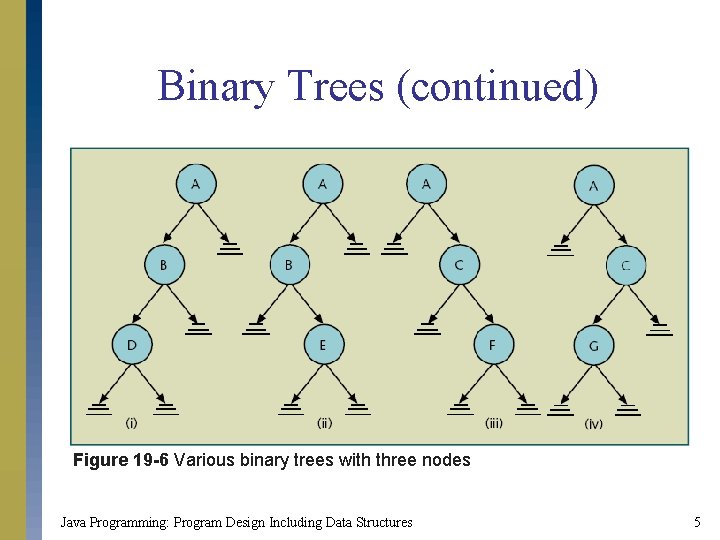
Binary Trees (continued) Figure 19 -6 Various binary trees with three nodes Java Programming: Program Design Including Data Structures 5

Binary Trees (continued) s You can write a class that represents each node in a binary tree s Called Binary. Tree. Node s Instance variables of the class Binary. Tree. Node s info: stores the information part of the node s l. Link: points to the root node of the left subtree s r. Link: points to the root node of the right subtree Java Programming: Program Design Including Data Structures 6

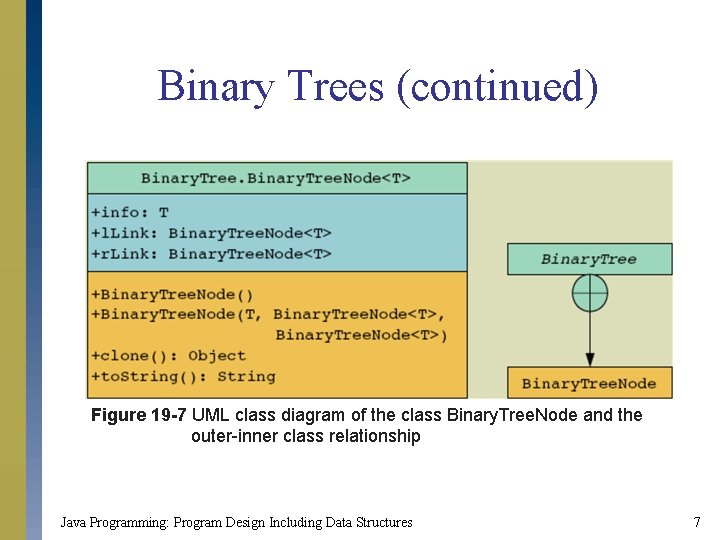
Binary Trees (continued) Figure 19 -7 UML class diagram of the class Binary. Tree. Node and the outer-inner class relationship Java Programming: Program Design Including Data Structures 7

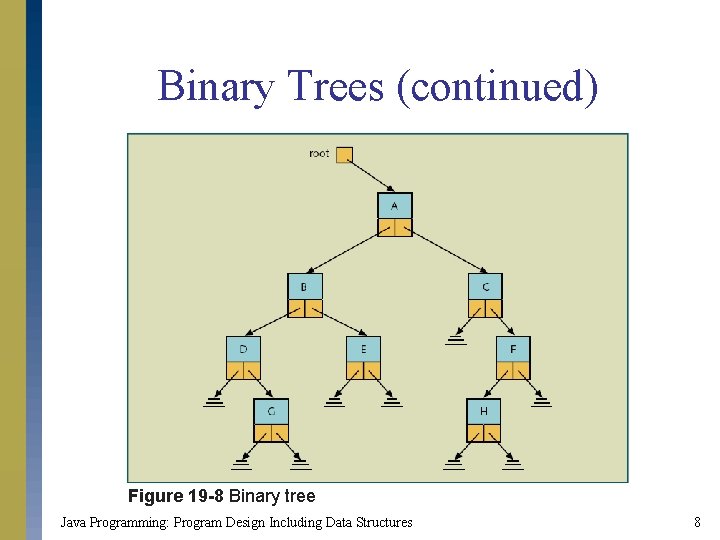
Binary Trees (continued) Figure 19 -8 Binary tree Java Programming: Program Design Including Data Structures 8

Binary Trees (continued) s A leaf is a node in a tree with no children s Let U and V be two nodes in a binary tree s U is called the parent of V if there is a branch from U to V s A path from a node X to a node Y is a sequence of nodes X 0, X 1, . . . , Xn such that: s X = X 0, Xn = Y s Xi-1 is the parent of Xi for all i = 1, 2, . . . , n Java Programming: Program Design Including Data Structures 9

Binary Trees (continued) s Length of a path s The number of branches on that path s Level of a node s The number of branches on the path from the root to the node s Height of a binary tree s The number of nodes on the longest path from the root to a leaf Java Programming: Program Design Including Data Structures 10

Binary Trees (continued) s Method height private int height(Binary. Tree. Node<T> p) { if (p == null) return 0; else return 1 + Math. max(height(p. l. Link), height(p. r. Link)); } Java Programming: Program Design Including Data Structures 11

Copy Tree s Method copy. Tree private Binary. Tree. Node<T> copy. Tree (Binary. Tree. Node<T> other. Tree. Root) { Binary. Tree. Node<T> temp; if (other. Tree. Root == null) temp = null; else { temp = (Binary. Tree. Node<T>) other. Tree. Root. clone(); temp. l. Link = copy. Tree(other. Tree. Root. l. Link); temp. r. Link = copy. Tree(other. Tree. Root. r. Link); } return temp; }//end copy. Tree Java Programming: Program Design Including Data Structures 12

Binary Tree Traversal s Item insertion, deletion, and lookup operations require that the binary tree be traversed s Commonly used traversals s Inorder traversal s Preorder traversal s Postorder traversal Java Programming: Program Design Including Data Structures 13

Inorder Traversal s Binary tree is traversed as follows: s Traverse left subtree s Visit node s Traverse right subtree Java Programming: Program Design Including Data Structures 14

Inorder Traversal (continued) s Method in. Order private void inorder(Binary. Tree. Node<T> p) { if (p != null) { inorder(p. l. Link); System. out. print(p + “ “); inorder(p. r. Link); } } Java Programming: Program Design Including Data Structures 15

Preorder Traversal s Binary tree is traversed as follows: s Visit node s Traverse left subtree s Traverse right subtree Java Programming: Program Design Including Data Structures 16

Preorder Traversal (continued) s Method pre. Order private void preorder(Binary. Tree. Node<T> p) { if (p != null) { System. out. print(p + “ “); preorder(p. l. Link); preorder(p. r. Link); } } Java Programming: Program Design Including Data Structures 17

Postorder Traversal s Binary tree is traversed as follows: s Traverse left subtree s Traverse right subtree s Visit node Java Programming: Program Design Including Data Structures 18

Postorder Traversal (continued) s Method post. Order private void postorder(Binary. Tree. Node<T> p) { if (p != null) { postorder(p. l. Link); postorder(p. r. Link); System. out. print(p + “ “); } } Java Programming: Program Design Including Data Structures 19

Implementing Binary Trees Figure 19 -11 UML class diagram of the interface Binary. Tree. ADT Java Programming: Program Design Including Data Structures 20

Implementing Binary Trees (continued) Figure 19 -12 UML class diagram of the class Binary. Tree Java Programming: Program Design Including Data Structures 21

Implementing Binary Trees (continued) s Method clone public Object clone() { Binary. Tree<T> copy = null; try { copy = (Binary. Tree<T>) super. clone(); } catch (Clone. Not. Supported. Exception e) { return null; } if (root != null) copy. root = copy. Tree(root); return copy; } Java Programming: Program Design Including Data Structures 22

Binary Search Trees s To search for an item in a normal binary tree, you must traverse entire tree until item is found s Search process will be very slow s Similar to searching in an arbitrary linked list s Binary search tree s Data in each node is s Larger than the data in its left child s Smaller than the data in its right child Java Programming: Program Design Including Data Structures 23

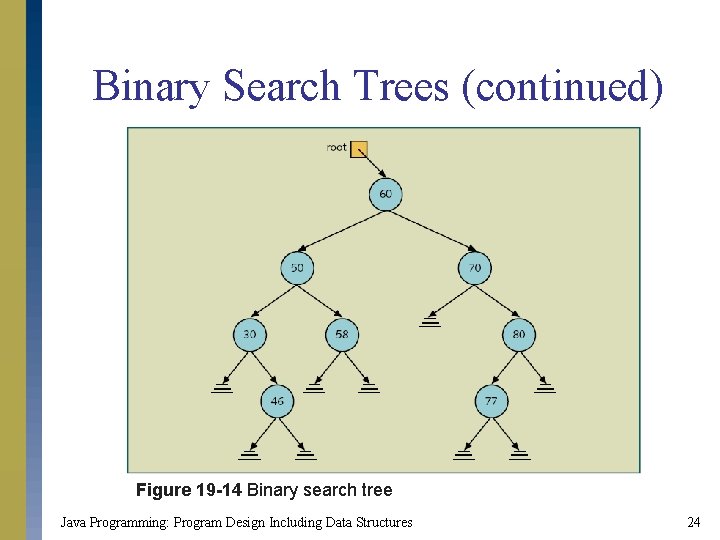
Binary Search Trees (continued) Figure 19 -14 Binary search tree Java Programming: Program Design Including Data Structures 24

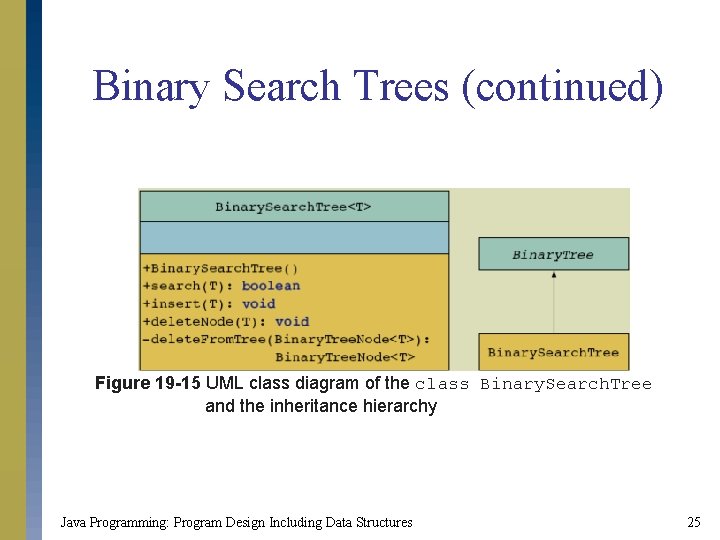
Binary Search Trees (continued) Figure 19 -15 UML class diagram of the class Binary. Search. Tree and the inheritance hierarchy Java Programming: Program Design Including Data Structures 25

Search s Searches tree for a given item s General steps s Compare item with info in root node s If they are the same, stop the search s If item is smaller than info in root node s Follow link to left subtree s Otherwise s Follow link to right subtree Java Programming: Program Design Including Data Structures 26

Insert s Inserts a new item into a binary search tree s General steps s Search tree and find the place where new item is to be inserted s Search algorithm is similar to method search s Insert new item s Duplicate items are not allowed Java Programming: Program Design Including Data Structures 27

Delete s Deletes item from a binary search tree s After deleting items, resulting tree must be a binary search tree s General steps s Search the tree for the item to be deleted s Searching algorithm is similar to method search s Delete item Java Programming: Program Design Including Data Structures 28

Delete (continued) s Delete operation has four cases s s Case 1: Node to be deleted is a leaf Case 2: Node to be deleted has no left subtree Case 3: Node to be deleted has no right subtree Case 4: Node to be deleted has nonempty left and right subtrees search left subtree of the node to be deleted to find its immediate predecessor Java Programming: Program Design Including Data Structures 29

Client Program (1) public class Binary. Trees { public static void main(String[] args) { // TODO code application logic here Binary. Search. Tree<Integer> A = new Binary. Search. Tree<>(); Binary. Search. Tree<Integer> B = new Binary. Search. Tree<>(); Binary. Search. Tree<Integer> C = new Binary. Search. Tree<>(); A. insert(10); A. insert(8); A. insert(1); A. insert(2); A. insert(3); A. insert(4); A. insert(5); B. insert(10); B. insert(8); B. insert(1); B. insert(2); B. insert(3); B. insert(4); B. insert(5); C. insert(23); C. insert(11); System. out. print("A & B are "); if(!A. similar. Trees(B. root)) System. out. print("NOT "); System. out. println("similar trees"); Java Programming: Program Design Including Data Structures 30

Client Program (2) B. insert(15); B. insert(25); System. out. print("After inserting 15 & 25 into B, A & B are "); if(!A. similar. Trees(B. root)) System. out. print("NOT "); System. out. println("similar trees"); System. out. print("A & C are "); if(!A. similar. Trees(C. root)) System. out. print("NOT "); System. out. println("similar trees"); System. out. print("A: "); A. inorder. Traversal(); int leaf. Count = A. tree. Leaf. Count(); int node. Count = A. tree. Node. Count(); System. out. println("Number of leaves of A = " + leaf. Count + ", Number of nodes of A = " + node. Count); System. out. print("n. B: "); B. inorder. Traversal(); leaf. Count = B. tree. Leaf. Count(); node. Count = B. tree. Node. Count(); System. out. println("Number of leaves of B = " + leaf. Count + ", Number of nodes of B = " + node. Count); System. out. print("n. C: "); C. inorder. Traversal(); leaf. Count = C. tree. Leaf. Count(); node. Count = C. tree. Node. Count(); System. out. println("Number of leaves of C = " + leaf. Count + ", Number of nodes of C = " + node. Count); } Java Programming: Program Design Including Data Structures 31

Binary Search Tree: Analysis s Performance depends on shape of the tree s If tree shape is linear, performance is the same as for a linked list s Average number of nodes visited 1. 39 log 2 n = O(log 2 n) s Average number of key comparisons 2. 77 log 2 n = O(log 2 n) Java Programming: Program Design Including Data Structures 32

Nonrecursive Binary Tree Traversal Algorithms s Traversal algorithms s Inorder s Preorder s Postorder Java Programming: Program Design Including Data Structures 33

Nonrecursive Inorder Traversal s Method non. Recursive. In. Traversal public void non. Recursive. In. Traversal() { Linked. Stack. Class<Binary. Tree. Node<T> > stack = new Linked. Stack. Class<Binary. Tree. Node<T> >(); Binary. Tree. Node<T> current; current = root; while ((current != null) || (!stack. is. Empty. Stack())) if (current != null) { stack. push(current); current = current. l. Link; } Java Programming: Program Design Including Data Structures 34

Nonrecursive Inorder Traversal (continued) else { current = (Binary. Tree. Node<T>) stack. peek(); stack. pop(); System. out. print(current. info + “ “); current = current. r. Link; } System. out. println(); } Java Programming: Program Design Including Data Structures 35

Nonrecursive Preorder Traversal s General algorithm create stack current = root; while (current is not null or stack is nonempty) if (current is not null) { visit current; push current onto stack; current = current. l. Link; } else { pop stack into current; current = current. r. Link; //prepare to visit right subtree } Java Programming: Program Design Including Data Structures 36

Nonrecursive Postorder Traversal s General algorithm s s s Mark left subtree of node as visited Visit left subtree and return to node Mark right subtree of node as visited Visit right subtree and return to node Visit node Java Programming: Program Design Including Data Structures 37

An Iterator to a Binary Tree s You can create an iterator for a binary tree (Textbook pp. 1380) s Iterator can traverse tree using s Inorder traversal s Preorder traversal s Postorder traversal Java Programming: Program Design Including Data Structures 38

AVL (Height-Balanced) Trees s Search performance depends on shape of the tree s You want the tree to be balanced s AVL (height-balanced) tree s Resulting binary search tree is nearly balanced s Perfectly balanced binary search tree s Heights of the left and right subtrees are equal s Left and right subtrees are perfectly balanced binary trees Java Programming: Program Design Including Data Structures 39

AVL (Height-Balanced) Trees(continued) Figure 19 -24 Perfectly balanced binary tree Java Programming: Program Design Including Data Structures 40

AVL (Height-Balanced) Trees (continued) s AVL tree: A binary search tree where s Heights of left and right subtrees differs by at most 1 s Left and right subtrees are AVL trees s Balance factor s Difference between height of right subtree and height of left subtree s Balance factor: the height of the right subtree – the height of the left subtree Java Programming: Program Design Including Data Structures 41

AVL (Height-Balanced) Trees (continued) Figure 19 -25 Perfectly balanced binary tree Java Programming: Program Design Including Data Structures 42

Insertion into AVL Trees s General steps s Search AVL tree to find insertion point s Insert new item s Duplicate items are not allowed s Rebalance tree (if needed) Java Programming: Program Design Including Data Structures 43

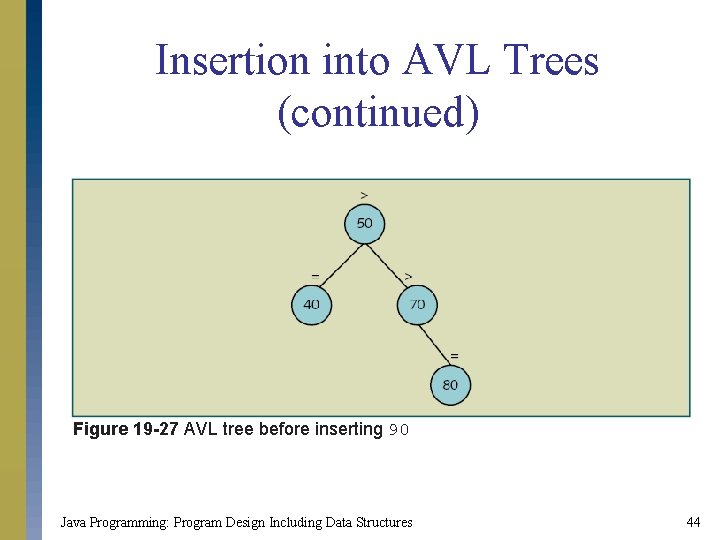
Insertion into AVL Trees (continued) Figure 19 -27 AVL tree before inserting 90 Java Programming: Program Design Including Data Structures 44

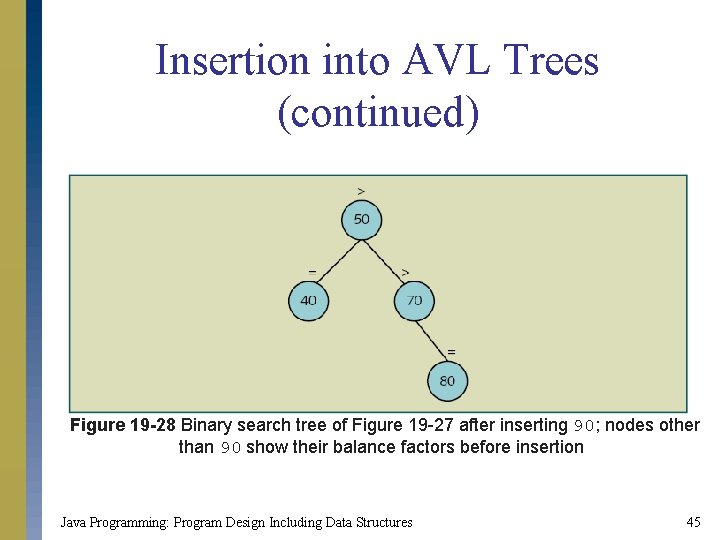
Insertion into AVL Trees (continued) Figure 19 -28 Binary search tree of Figure 19 -27 after inserting 90; nodes other than 90 show their balance factors before insertion Java Programming: Program Design Including Data Structures 45

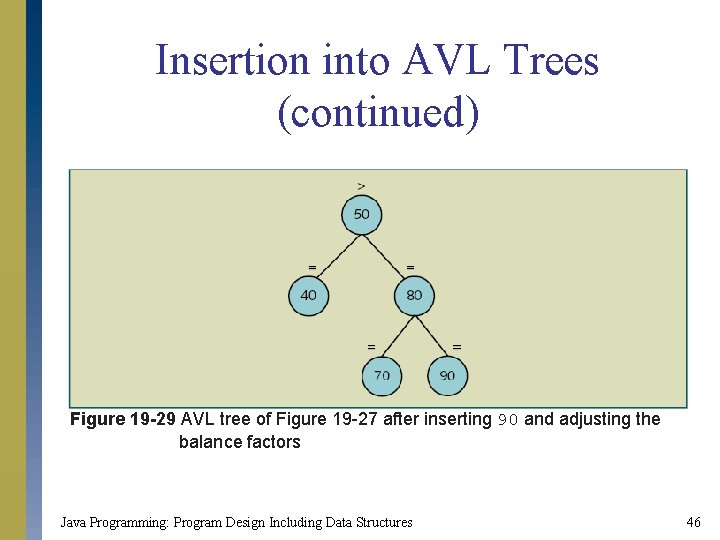
Insertion into AVL Trees (continued) Figure 19 -29 AVL tree of Figure 19 -27 after inserting 90 and adjusting the balance factors Java Programming: Program Design Including Data Structures 46

AVL Tree Rotations s Reconstruction procedure s Types of rotations s Left rotation s Nodes from right subtree move to left subtree s Root of right subtree becomes root of reconstructed subtree s Right rotation s Nodes from left subtree move to right subtree s Root of left subtree becomes root of reconstructed subtree Java Programming: Program Design Including Data Structures 47

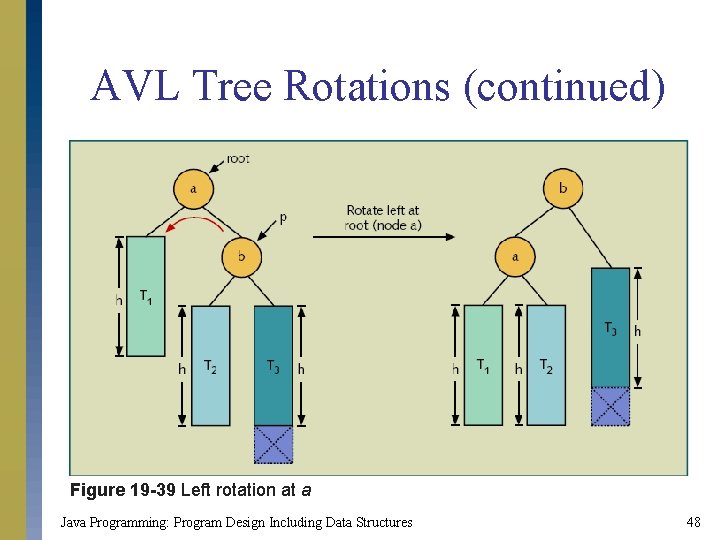
AVL Tree Rotations (continued) Figure 19 -39 Left rotation at a Java Programming: Program Design Including Data Structures 48

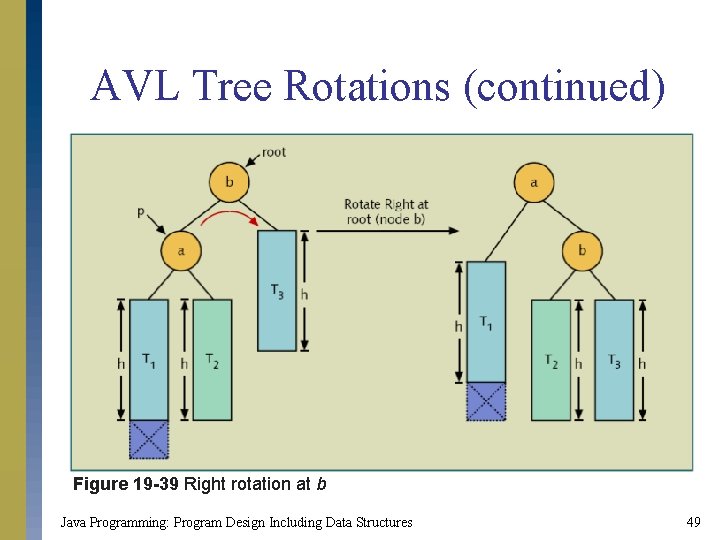
AVL Tree Rotations (continued) Figure 19 -39 Right rotation at b Java Programming: Program Design Including Data Structures 49

AVL Tree Rotations (continued) s Method rotate. To. Left private AVLNode<T> rotate. To. Left(AVLNode<T> root) { AVLNode<T> p; //reference variable to the root of the right subtree of root if (root == null) System. err. println(“Error in the tree. ”); else if (root. r. Link == null) System. err. println(“Error in the tree: “ + “No right subtree to rotate. ”); else { p = root. r. Link; root. r. Link = p. l. Link; //the left subtree of p becomes the right //subtree of root p. l. Link = root; root = p; //make p the new root node } return root; }//end rotate. To. Left Java Programming: Program Design Including Data Structures 50

AVL Tree Rotations (continued) s Method rotate. To. Right private AVLNode<T> rotate. To. Right(AVLNode<T> root) { AVLNode<T> p; //reference variable to the root of the //left subtree of root if (root == null) System. err. println(“Error in the tree. ”); else if (root. l. Link == null) System. err. println(“Error in the tree: “ + “No left subtree to rotate. ”); else { p = root. l. Link; root. l. Link = p. r. Link; //the right subtree of p //becomes the left subtree of root p. r. Link = root; root = p; //make p the new root node } return root; }//end rotate. To. Right Java Programming: Program Design Including Data Structures 51

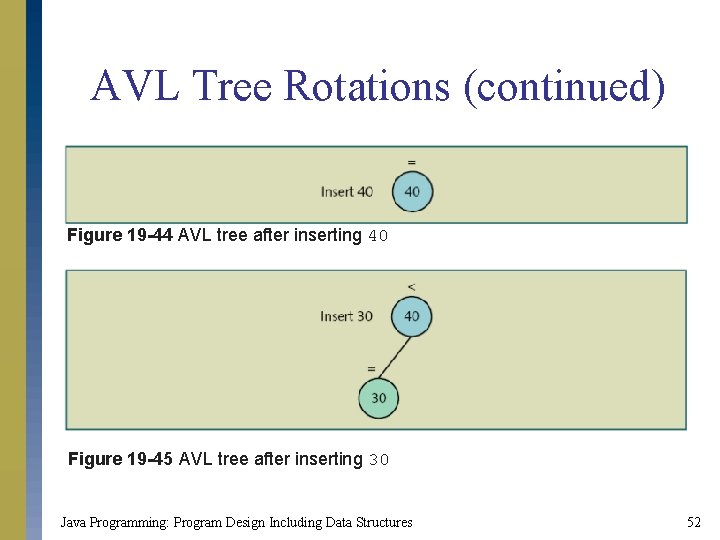
AVL Tree Rotations (continued) Figure 19 -44 AVL tree after inserting 40 Figure 19 -45 AVL tree after inserting 30 Java Programming: Program Design Including Data Structures 52

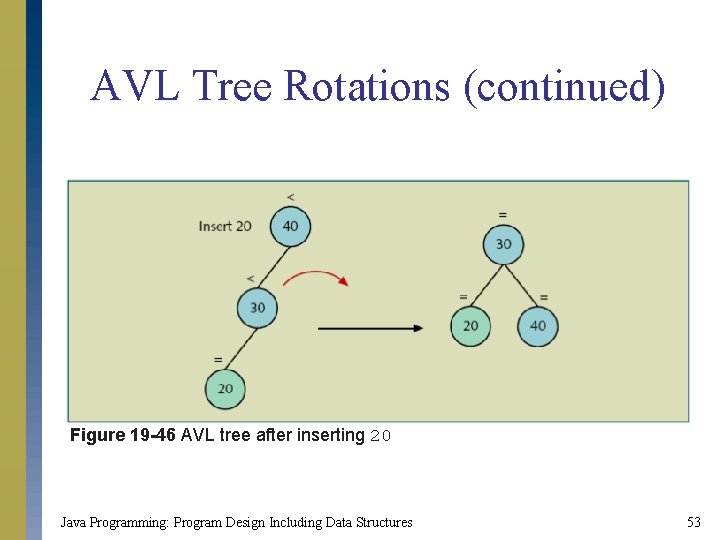
AVL Tree Rotations (continued) Figure 19 -46 AVL tree after inserting 20 Java Programming: Program Design Including Data Structures 53

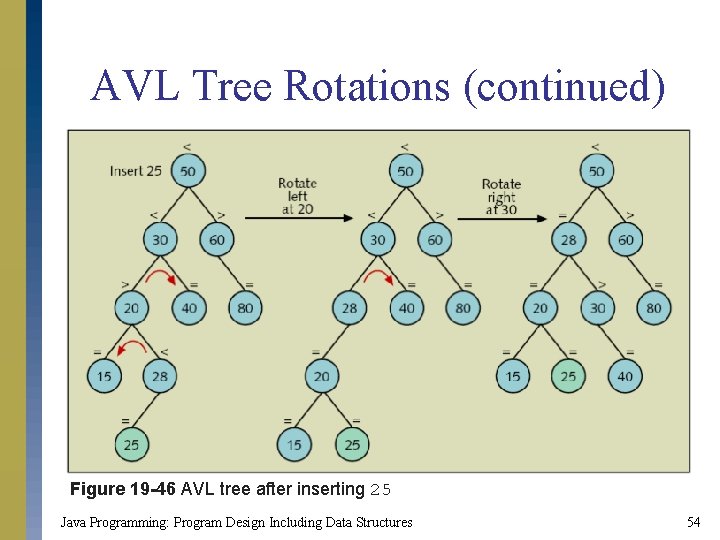
AVL Tree Rotations (continued) Figure 19 -46 AVL tree after inserting 25 Java Programming: Program Design Including Data Structures 54

Deletion from AVL Trees s General steps s Find node to be deleted s Delete node s Four cases arise: s s Node to be deleted is a leaf Node to be deleted has no right child Node to be deleted has no left child Node to be deleted has both children Java Programming: Program Design Including Data Structures 55

Analysis: AVL Trees s Height of AVL tree with n nodes (worst case) 1. 44 log 2 n = O(log 2 n) s Time to manipulate an AVL tree in the worst case is no more than 44% of optimum time s Average search time of an AVL tree is about 4% more than the optimum Java Programming: Program Design Including Data Structures 56

Programming Example: Video Store (Revisited) s Program in Chapter 16 used a linked list to keep track of video inventory s Search could be time consuming s Modify program to use a binary tree instead s Insertion and deletion in a binary search tree is faster than in a linked list Java Programming: Program Design Including Data Structures 57

Chapter Summary s Binary trees s Every node has only two children s Left subtree s Right subtree s Binary tree traversal s Inorder s Preorder s Postorder Java Programming: Program Design Including Data Structures 58

Chapter Summary (continued) s Binary search trees s Each node is greater than elements in its left subtree and less than elements in its right subtree s AVL (height-balanced) trees s Binary search tree s Heights of left and right subtrees differs by at most 1 s Left and right subtrees of the root node are AVL trees Java Programming: Program Design Including Data Structures 59