Chapter 19 Analysis of Variance ANOVA ANOVA How

Chapter 19 Analysis of Variance (ANOVA)

ANOVA • How to test a null hypothesis that the means of more than two populations are equal. H 0: 1 = 2 = 3 H 1: Not all three populations are equal • Test hypothesis with ANOVA procedure (Analysis of variance) • ANOVA tests use the F distribution

F Distribution • F distribution has 2 numbers of degree of freedom (DF) -- numerator and denominator. – EXAMPLE: df = (8, 14) • Change in numerator df has a greater effect on the shape of the distribution. • Properties: – Continuous and skewed to the right – Has 2 df numbers – Nonnegative unites.

Finding the F value Example 19. 1 SITUATION: Find the F value for 8 degrees of freedom for the numerator, 14 degrees of freedom for the denominator and. 05 area in the right tail of the F curve. • Consult Table V of Appendix A – corresponding to. 05 area. – Locate the numerator on the top row, and the denominator along the left. – Find where they intersect. • This will give the critical value of F. • Excel: FDIST (x, df 1, df 2), FINV(prob. , df 1, df 2)

Assumptions in ANOVA To test H 0: 1= 2= 3 H 1: Not all three populations are equal – The following must be true: • Population from which samples are drawn are normally distributed • Population from which the samples are drawn have the same variance (or standard deviation) • The samples are drawn from different populations that are random and independent.

How does ANOVA work? • The purpose of ANOVA is to test differences in means (for groups or variables) for statistical significance. • By partitioning the total variance into the component that is due to true random error (i. e. , within-group SSE) and the components that are due to differences between groups (SSG). • SSG is then tested for statistical significance, and, if significant, the null hypothesis of no differences between means is rejected. • Always right-tailed with the rejection region in the right tail

Types of ANOVA • One-way ANOVA: Only one factor is considered • Two-way ANOVA – Answer the question if the tow categorical variables act together to impact the averages for the various groups? – If the two factors do not act together to impact the averages, does at least one of the factors have an impact on the averages for the various groups? • N-way ANOVA – Looking for interaction of multiple factors. – Requires more data – Always right-tailed with the rejection region in the right tail

ANOVA Notation and Formulas • • xi = sample mean for group (or treatment) i k = the number of groups (or treatments) ni = sample size of group i x = the average (the grand mean) of all of the observations in all groups • n = sum of the k sample sizes = n 1 + n 2 + n 3 …. + nk • si 2 = the sample variance for group (or treatment) i

MSG and MSE • Sum of squares for groups (SSG) • Mean squares for groups (MSG) • Sum of squared error (SSE) • Mean squared error (MSE)

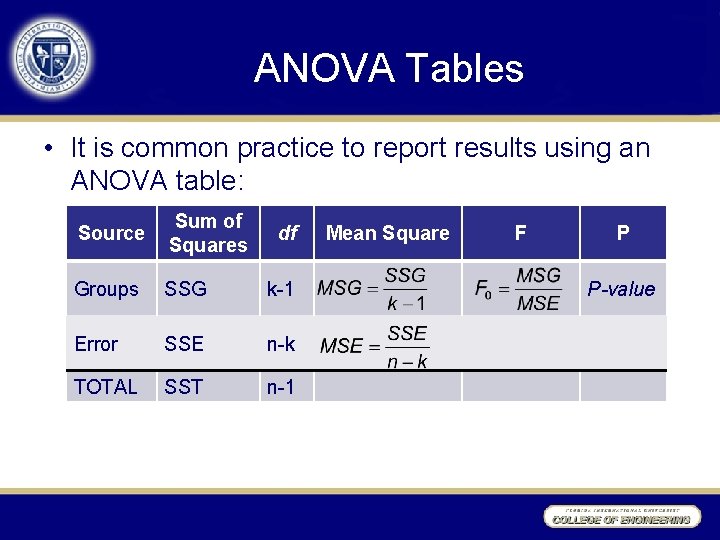
SST and relationship among the SSs • Total sum of squares (SST) – SST is the numerator when calculating sample variance – Does not include a group distinction – Dividing SST by its df sample variance • Relationships df Groups Error Total k-1 n-k n-1 SSG + SSE = SST

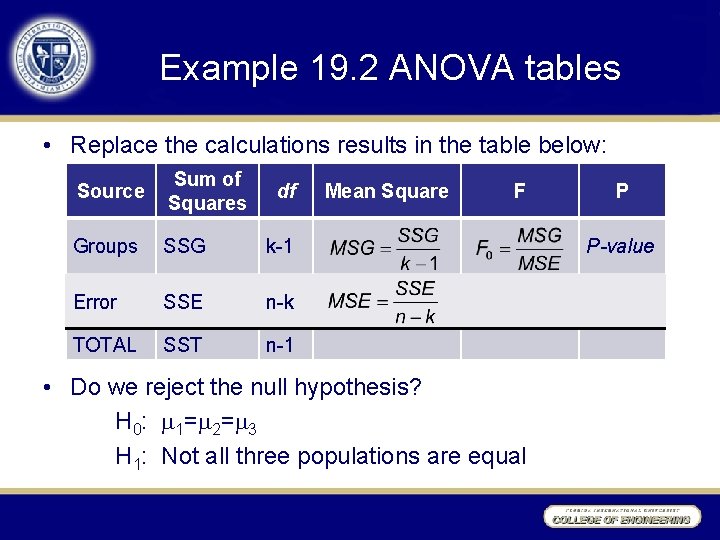
ANOVA Tables • It is common practice to report results using an ANOVA table: Source Sum of Squares Groups SSG k-1 Error SSE n-k TOTAL SST n-1 df Mean Square F P P-value

ANOVA process by hand Example 19. 2 SITUATION: Soap manufacturer wants to test 3 new machines that should fill a jug. They tested for 5 hours and recorded the number of jugs filled by each per hour: – At the 10% significance level can we reject the null hypothesis that the mean number of jugs filled per hour by each machine is the same? • k = 3 • n 1= n 2 =n 3 = 5 continued…. Machine 1 Machine 2 Machine 3 54 53 49 49 56 53 52 57 47 55 51 50 48 59 54

ANOVA process by hand Example 19. 2 continued • We now need to calculate the ANOVA table • For machine 1: • Now do the same for machine 2 & 3 • Then for 1 -3 combined

ANOVA process by hand Example 19. 2 continued • Then we can calculate SSG/E/T: SST =SSG + SSE = 58. 5335 + 111. 2 = 169. 7335 • Degrees of freedom – Group df = k-1 = 3 -1 = 2 – Error df = n-k = 15 -3 = 12 – Total df = n-1 = 15 -1 = 14

ANOVA process by hand Example 19. 2 continued • Now calculate MSG, MSE, and F • Determine if the assumption that the three populations have the same population variance are valid. The assumption is reasonable if: • Now, look in Table V of Appendix A. Use numerator df=2, denominator df=12 ….

Example 19. 2 ANOVA tables • Replace the calculations results in the table below: Source Sum of Squares Groups SSG k-1 Error SSE n-k TOTAL SST n-1 df Mean Square F • Do we reject the null hypothesis? H 0: 1= 2= 3 H 1: Not all three populations are equal P P-value

Example 19. 2 by Excel Anova: Single Factor M 1 54 49 52 55 48 M 2 53 56 57 51 59 M 3 49 53 47 50 54 SUMMARY Groups M 1 M 2 M 3 Count 5 5 5 Sum Average Variance 258 51. 6 9. 3 276 55. 2 10. 2 253 50. 6 8. 3 ANOVA Source of Variation SS Between Groups 58. 53333 Within Groups 111. 2 2 12 29. 26667 3. 158273 0. 079073 2. 806796 9. 266667 Total 14 169. 7333 df MS F P-value F crit

Example 19. 2 by Minitab One-way ANOVA: P versus M Source DF SS MS F P M 2 58. 53 29. 27 3. 16 0. 079 Error 12 111. 20 9. 27 Total 14 169. 73 S = 3. 044 R-Sq = 34. 49% R-Sq(adj) = 23. 57% Individual 95% CIs For Mean Based on Pooled St. Dev Level N Mean St. Dev -+---------+-----+-------M 1 5 51. 600 3. 050 (-----*-----) M 2 5 55. 200 3. 194 (-----*-----) M 3 5 50. 600 2. 881 (-----*-----) -+---------+-----+------- 48. 0 51. 0 54. 0 57. 0 Pooled St. Dev = 3. 044

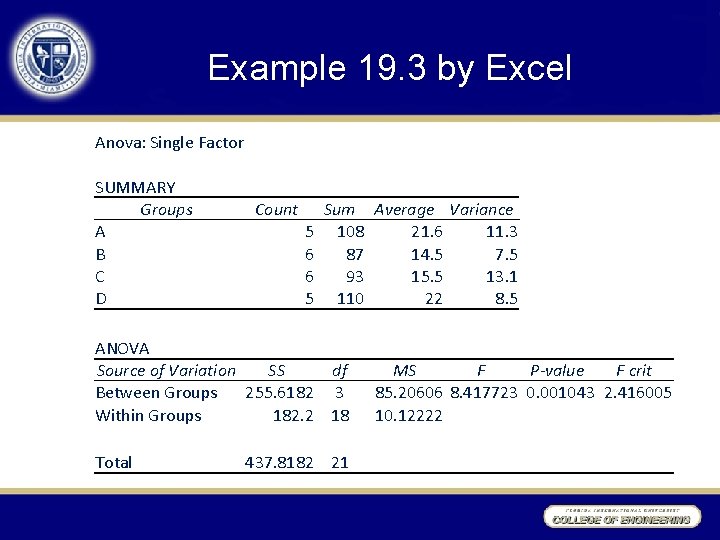
Example 19. 3 by Excel Anova: Single Factor SUMMARY Groups A B C D Count 5 6 6 5 Sum Average Variance 108 21. 6 11. 3 87 14. 5 7. 5 93 15. 5 13. 1 110 22 8. 5 ANOVA Source of Variation SS df Between Groups 255. 6182 3 Within Groups 182. 2 18 Total 437. 8182 21 MS F P-value F crit 85. 20606 8. 417723 0. 001043 2. 416005 10. 12222

Example 19. 3 by Minitab One-way ANOVA: Cus. versus Teller Source DF SS MS F P Teller 3 255. 6 85. 2 8. 42 0. 001 Error 18 182. 2 10. 1 Total 21 437. 8 S = 3. 182 R-Sq = 58. 38% R-Sq(adj) = 51. 45% Individual 95% CIs For Mean Based on Pooled St. Dev Level N Mean St. Dev ------+---------+-----+--A 5 21. 600 3. 362 (----*-------) B 6 14. 500 2. 739 (------*-------) C 6 15. 500 3. 619 (-------*-------) D 5 22. 000 2. 915 (----*-------) ------+---------+-----+-- 14. 0 17. 5 21. 0 24. 5 Pooled St. Dev = 3. 182

Pairwise Comparisons • If the result of ANOVA is to reject the null hypothesis, it does not identify which group means are significantly different. • Most software packages include this comparison. – Calculate a confidence interval for the differences of each unique pair of means. – Check to see if ZERO falls in the interval, if not then they are significantly different.

Example 19. 3 by Minitab Fisher 95% Individual Confidence Intervals All Pairwise Comparisons Simultaneous confidence level = 80. 96% A subtracted from: Lower Center B -11. 147 -7. 100 C -10. 147 -6. 100 D -3. 827 0. 400 Upper ---------+---------+ -3. 053 (------*------) -2. 053 (------*------) 4. 627 (------*------) ---------+---------+ -6. 0 0. 0 6. 0 12. 0 B subtracted from: Lower Center Upper ---------+---------+ C -2. 859 1. 000 4. 859 (------*-----) D 3. 453 7. 500 11. 547 (------*-----) ---------+---------+ -6. 0 0. 0 6. 0 12. 0 C subtracted from: Lower Center Upper ---------+---------+ D 2. 453 6. 500 10. 547 (------*------) ---------+---------+ -6. 0 0. 0 6. 0 12. 0

Pairwise Comparisons Fisher’s Least Significant Difference (LSD) Method • Null Hypothesis: H 0: i = j • Least Significant Difference (LSD) : • The pair of means i and j is declared significantly different if

Example 19. 3 with LSD n Teller A 5 21. 6 Teller B 6 14. 5 Teller C 6 15. 5 Teller D 5 22. 0

Example 19. 3 with LSD ni nj LSD Teller A-B 5 6 Teller A-C 5 Teller A-D 21. 6 7. 1 4. 71 6 6. 1 4. 71 5 5 0. 4 4. 91 Teller B-C 6 6 14. 5 1. 0 4. 49 Teller B-D 6 5 14. 5 7. 5 4. 71 Teller C-D 6 5 15. 5 6. 5 4. 71

Welch’s Approach to Heterogeneity of Variance • If Max(sj 2)/Min(sj 2)>2, the assumption of equal variance can not be used. • Welch’s approach modifies the F-test with the following steps: – – For each sample j, calculate wj Calculate the summation of w from k samples Calculate the weighted avg. of sample means Calculate the test statistic F 0 and df