Chapter 18 Query Processing and Optimization Chapter Outline

Chapter 18 Query Processing and Optimization

Chapter Outline u Introduction . u Using Heuristics in Query Optimization – Query Trees and Query Graphs – Transformation Rules for RA expressions – Heuristic Optimization

Introduction u With declarative languages such as SQL, user specifies what data is required rather than how it is to be retrieved. u Relieves user of knowing what constitutes good execution strategy. Also gives DBMS more control over system performance. Two main techniques for query optimization: – heuristic rules that order operations in a query. – comparing different strategies based on relative costs, and selecting one that minimizes resource usage. u u

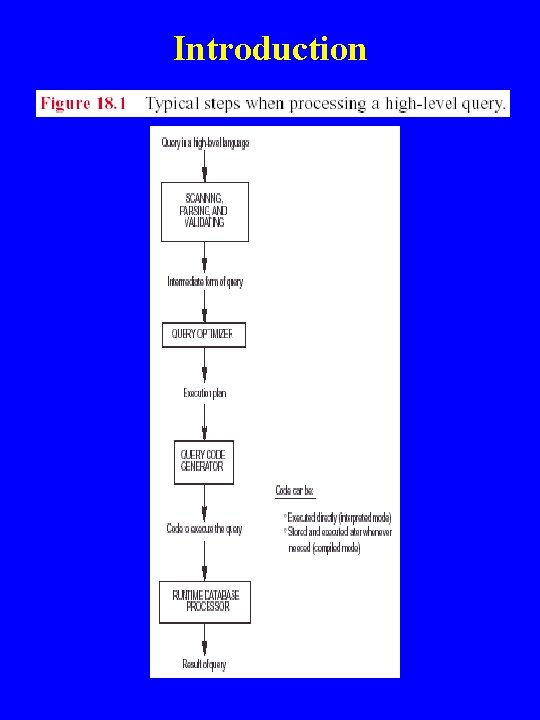
Introduction u Query Processing (QP) : Activities involved in retrieving data from the database. Aims of QP: – transform query written in high-level language (e. g. SQL), into correct and efficient execution strategy expressed in low-level language (implementing RA); – execute the strategy to retrieve required data. Query Optimization (QO): Activity of choosing an efficient execution strategy for processing query. u u As there are many equivalent transformations of same high-level query, aim of QO is to choose one that minimizes resource usage. Generally, reduce total execution time of query. May also reduce response time of query. Problem computationally intractable with large number of relations, so strategy adopted is reduced to finding near optimum solution.

Introduction

Query Trees and Query Graphs

Transformation Rules for RA Operations u Cascade of Selection: Conjunctive selection operations can cascade into individual selection operations sp q r(R) = sp (sq ( sr (R))) u Commutativity of selection. sp (sq (R)) = sq ( sp(R)) u In a sequence of projection operations, only the last in the sequence is required. Cascade of Projection: L M … N (R) = L (R) u Commutativity of s and : If the selection condition c involves only those attributes A 1, … An in the projection list, then the two operations can commute: Ai, …, Am (sc (R)) = sc ( Ai, …, Am(R))

Transformation Rules for RA Operations u Commutativity of (and ). R p S = S p R R S=S R u Associativity of (and ). and natural join (*)are always associative: (R * S) T = R * (S * T) (R S) T = R (S T) If join condition q involves attributes only from S and T, then is associative as follows: (R p S) q r T = R p r (S q T)

Transformation Rules for RA Operations u Commutativity of s and (or ). If all the attributes in the selection condition c involves only the attributes of one of the relations being joined – Say R – then the two operations can be commuted as follows: sc (R r S) = (sc (R)) r S sc (R S) = (sc (R)) S Alternatively if the condition c can be written as (c 1 and c 2), where condition c 1 involves only the attributes of the relations R and condition c 2 involves only the attributes of the relations S then the two operations can be commuted as follows: sc 1 (R r S) = (sc 1 (R)) r (sc 2 ( S)) sc 1 (R S) = (sc 1 (R)) (sc 2 ( S))

Transformation Rules for RA Operations u Commutativity of and (or ). projection If list of is form L= LL 1 where Lonly 2, 1 involves attributes of R, and L 2 only involves attributes of S, provided join condition only contains attributes of L, projection and theta-join operations commute as: L 1 L 2 (R r S) = ( L 1(R)) r ( L 2(S)) If join condition contains additional attributes not in L, say attributes M = M 1 M 2 where M 1 only involves attributes of R, and M 2 only involves attributes of S, a final projection operation is required: L 1 L 2(R r S) = L 1 L 2( ( L 1 M 1(R)) r ( L 2 M 2(S))) u Commutativity of and (but not - ). R S=S R u Associativity of and (but not - ). (R S) T = S (R T)

Transformation Rules for RA Operations Commutativity of s and set operations ( , , and -). sp(R S) = sp(S) sp(R) sp(R - S) = sp(S) - sp(R) u Commutativity of and . L (R S) = L(S) L(R)

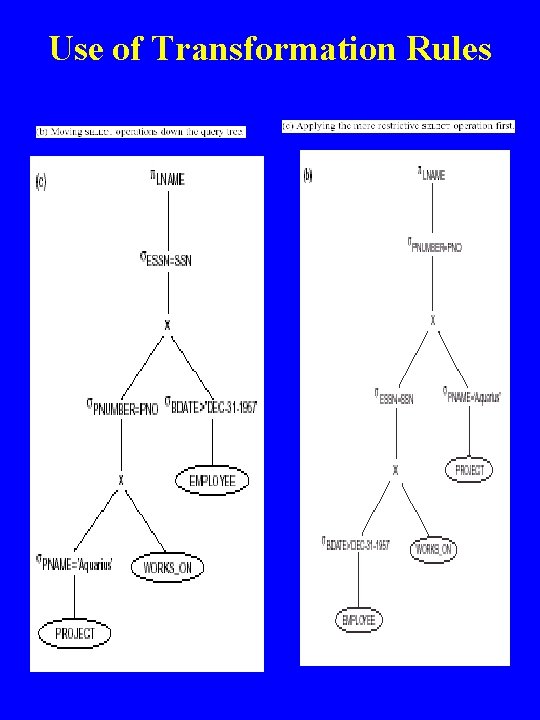
Heuristical Processing Strategies u Perform selection operations as early as possible. – Keep predicates on same relation together. u Combine Cartesian product with subsequent selection whose predicate represents join condition into a join operation. u Use associativity of binary operations to rearrange leaf nodes so leaf nodes with most restrictive selection operations executed first. u Perform projection as early as possible. – u Keep projection attributes on same relation together. Compute common expressions once. – If common expression appears more than once, and result not too large, store result and reuse it when required. – Useful when querying views, as same expression is used to construct view each time.

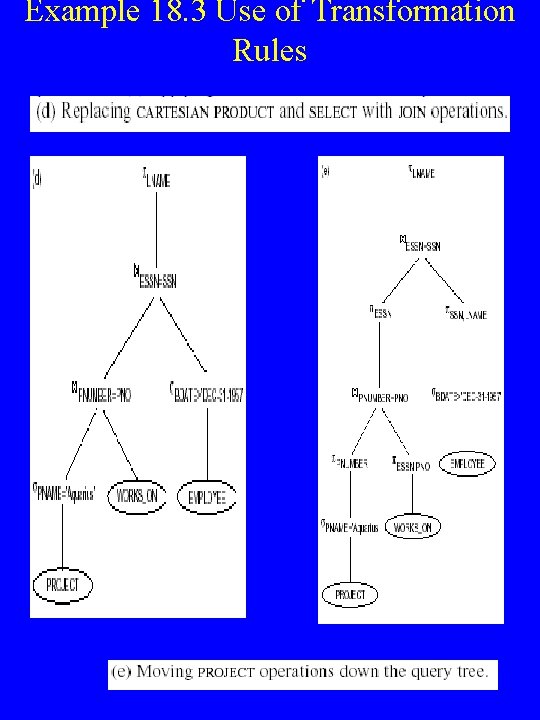
Use of Transformation Rules Q: Find the last name of employees born after 1975 who work on a project named ‘Aquarius’. SELECT FROM WHERE LNAME, EMPLOYEE, WORKS_ON, PROJECT, PNAME=‘Aquarius’ AND ESSN= SSN AND PNUMBER=PNO AND BDATE > ‘ 1957 -12 -31’

Use of Transformation Rules

Example 18. 3 Use of Transformation Rules