CHAPTER 18 Electrochemistry Oxidation Number An oxidation number

CHAPTER 18 Electrochemistry

Oxidation Number An oxidation number is a number assigned to an atom in a molecule or ion indicating whether that atom is electron rich (negative oxidation number), electron poor (positive oxidation number), or neutral (oxidation number of zero). Oxidation numbers do not indicate charges of atoms, but changes in oxidation number indicate whether atoms have gained or lost electron density. A reaction where some of the oxidation numbers change in going from reactants to products is called an oxidation-reduction (redox) reaction.

Rules For Assigning Oxidation Numbers 1) The sum of the oxidation numbers of a species is equal to the charge of the species. 2) Atoms in elemental forms have an oxidation number of 0. 3) Hydrogen has an oxidation number of +1 when bonded with nonmetals (molecular compounds) and -1 when combined with metals (ionic compounds). 4) Oxygen usually has an oxidation number of -2. Exceptions: Elemental forms, peroxides (H 2 O 2), OF 2. H 2 O 2 H +1, O -1 OF 2 F -1, O +2 5) Halogens. F in compounds is always -1. Other halogens are often -1, but in compounds with oxygen or other halogens the oxidation number may take on different values. 6) For assigning oxidation numbers in ionic compounds, it is useful to break the compounds up into ions.

Examples: Assign oxidation numbers for each atom in the following substances. H 2 O Fe(NO 3)2 SO 42 O 3 Mn. O 4 CO 2

H 2 O H = +1; O = -2 Fe(NO 3)2 = Fe 2+ and NO 3 so Fe = +2, O = -2, and so N = +5 SO 42 - O = -2, and so S = +6 O 3 elemental form, so O = 0 Mn. O 4 - O = -2, and so Mn = +7 CO 2 O = -2 and so C = +4

Oxidation-Reduction Reactions In an oxidation-reduction (redox) reaction the oxidation numbers of some of the atoms involved in the reaction change in going from reactants to products. 2 Fe 2 O 3(s) + 3 C(s) 4 Fe(s) + 3 CO 2(g) +3 -2 0 0 +4 -2 We use the following terms in reference to redox reactions. Oxidation - An increase in the value for the oxidation number. Reduction - A decrease in the value for the oxidation number. There will always be one oxidation and one reduction process per reaction. C 0 to +4, and so is oxidized. Fe +3 to 0, and so is reduced.

Oxidizing and Reducing Agents We call the species that is oxidized in a redox reaction the reducing agent, and the species that is reduced in a redox reaction an oxidizing agent. This seems confusing, but is based on the idea that there must be both an oxidation and a reduction taking place in a redox reaction. SO 2(g) + 2 Fe 3+(aq) + 2 H 2 O(l) 2 Fe 2+(aq) + SO 42 -(aq) + 4 H+(aq) +4 -2 +3 +1 -2 +2 +6 -2 +1 In the above reaction S is oxidized (from +4 to +6) and so SO 2 is a reducing agent, and Fe is reduced (from +3 to +2) and so Fe 3+ is an oxidizing agent.

Balancing Oxidation-Reduction Reactions (acid or base conditions) 1) Write the unbalanced net ionic equation. 2) Assign oxidation numbers; identify the substance being oxidized and the substance being reduced. 3) Write balanced half reactions for oxidation and reduction. Include electrons as products (oxidation) or reactants (reduction) to change oxidation numbers. You may use H 2 O and H+ in balancing the half reactions. 4) If necessary, multiply one or both of the half reactions by whole numbers to get the electrons to cancel. 5) Combine the half reactions to get the net ionic equation. 6) If the reaction is carried out in base conditions, add OH- to both sides of the equation to cancel any H+ ions present.

Example: Balance the following reaction for acid conditions. Ag+(aq) + Cu(s) Ag(s) + Cu 2+(aq)

Example: Balance the following reaction for acid conditions. Ag+(aq) + Cu(s) Ag(s) + Cu 2+(aq) +1 0 0 ox Cu(s) Cu 2+ + 2 e- red Ag+(aq) + e- Ag(s) +2 Need to multiply the reduction reaction by 2 to get electrons to cancel. ox Cu(s) Cu 2+ + 2 e- red 2 Ag+(aq) + 2 e- 2 Ag(s) net Cu(s) + 2 Ag+(aq) Cu 2+(aq) + 2 Ag(s)

Example: Balance the following reaction for acid conditions. Pb. O 2(s) + Mn 2+(aq) Pb 2+(aq) + Mn. O 4 -(aq)

Example: Balance the following reaction for acid conditions. Pb. O 2(s) + Mn 2+(aq) Pb 2+(aq) + Mn. O 4 -(aq) +4 -2 ox +2 +2 +7 -2 Mn 2+(aq) Mn. O 4 -(aq) + 5 e. Mn 2+(aq) + 4 H 2 O( ) Mn. O 4 -(aq) + 5 e- + 8 H+(aq) red Pb. O 2(s) + 2 e- Pb 2+(aq) Pb. O 2(s) + 2 e- + 4 H+(aq) Pb 2+(aq) + 2 H 2 O( ) Now, must multiply the oxidation reaction by 2 and the reduction reaction by 5 to get electrons to cancel, giving us ox 2 Mn 2+(aq) + 8 H 2 O( ) 2 Mn. O 4 -(aq) + 10 e- + 16 H+(aq) red 5 Pb. O 2(s) + 10 e- + 20 H+(aq) 5 Pb 2+(aq) + 10 H 2 O( ) net 2 Mn 2+(aq) + 5 Pb. O 2(s) + 4 H+(aq) 2 Mn. O 4 -(aq) + 5 Pb 2+(aq) + 2 H 2 O( )

Example: Balance the following reaction for base conditions. Se. O 32 -(aq) + Cl 2(g) Se. O 42 -(aq) + Cl-(aq)

Example: Balance the following reaction for base conditions. Se. O 32 -(aq) + Cl 2(g) Se. O 42 -(aq) + Cl-(aq) +4 -2 ox 0 +6 -2 -1 Se. O 32 -(aq) Se. O 42 -(aq) + 2 e. Se. O 32 -(aq) + H 2 O( ) Se. O 42 -(aq) + 2 e- + 2 H+(aq) red Cl 2(g) + 2 e- 2 Cl-(aq) ox Se. O 32 -(aq) + H 2 O( ) Se. O 42 -(aq) + 2 e- + 2 H+(aq) red Cl 2(g) + 2 e- 2 Cl-(aq) net Se. O 32 -(aq) + Cl 2(g) + H 2 O( ) Se. O 42 -(aq) + 2 Cl-(aq) + 2 H+(aq) 2 OH-(aq) base Se. O 32 -(aq) + Cl 2(g) + 2 OH-(aq) Se. O 42 -(aq) + 2 Cl-(aq) + H 2 O( ) Notice that to balance for base conditions we add OH-(aq) to convert all H+(aq) ions into H 2 O( ).

Oxidation-reduction (redox) titration Just as we can titrate an acid with a base (or a base with an acid) we can react an oxidizing agent and a reducing agent in an oxidationreduction (redox) titration. The calculations involved in redox titrations are essentially the same as in acid-base titrations. Example: A solution containing the oxalate ion (C 2 O 42 -) can be titrated with permanganate ion (Mn. O 4 -). The redox reaction that occurs is 2 Mn. O 4 -(aq) + 5 C 2 O 42 -(aq) + 16 H+(aq) 2 Mn 2+(aq) + 10 CO 2(aq) + 8 H 2 O(l) A 25. 00 m. L sample from a stock solution of potassium oxalate is titrated with a 0. 0827 M solution of potassium permanganate. After the addition of 17. 48 m. L of permanganate solution the equivalence point of the titration is reached. What is the original concentration of oxalate ion in the stock solution of potassium oxalate?

2 Mn. O 4 -(aq) + 5 C 2 O 42 -(aq) + 16 H+(aq) 2 Mn 2+(aq) + 10 CO 2(aq) + 8 H 2 O(l) A 25. 00 m. L sample from a stock solution of potassium oxalate is titrated with a 0. 0827 M solution of potassium permanganate. After the addition of 17. 48 m. L of permanganate solution the equivalence point of the titration is reached. What is the original concentration of oxalate ion in the stock solution of potassium oxalate? moles Mn. O 4 - = 0. 01748 m. L 0. 0827 mol = 1. 446 x 10 -3 mol L soln moles C 2 O 42 - = 1. 446 x 10 -3 mol Mn. O 4 - 5 mol C 2 O 422 mol Mn. O 4= 3. 614 x 10 -3 mol C 2 O 42[C 2 O 42 -] = 3. 614 x 10 -3 mol = 0. 1446 M 0. 02500 L

Electrochemical Cells An electrochemical cell is a device that can interconvert chemical and electrical energy. There are two general types of cells: Galvanic cell (battery) - In a galvanic cell a chemical reaction is used to generate a voltage. Electrolytic cell - In an electrolytic cell an external voltage is used to drive a chemical reaction in a particular direction.

Galvanic Cells In a galvanic cell a chemical reaction is used to generate a voltage. There will be a half-cell oxidation reaction and a half-cell reduction reaction, which combine to give the net cell reaction. The sites where the oxidation and reduction reactions take place are called electrodes. By convention anode - electrode where oxidation reaction occurs cathode - electrode where reduction reaction occurs In a galvanic cell the anode is negative and the cathode is positive. Current flow is from the anode to the cathode. Salt bridge - A gel containing ions that can transfer charge and therefore complete the electrical circuit.

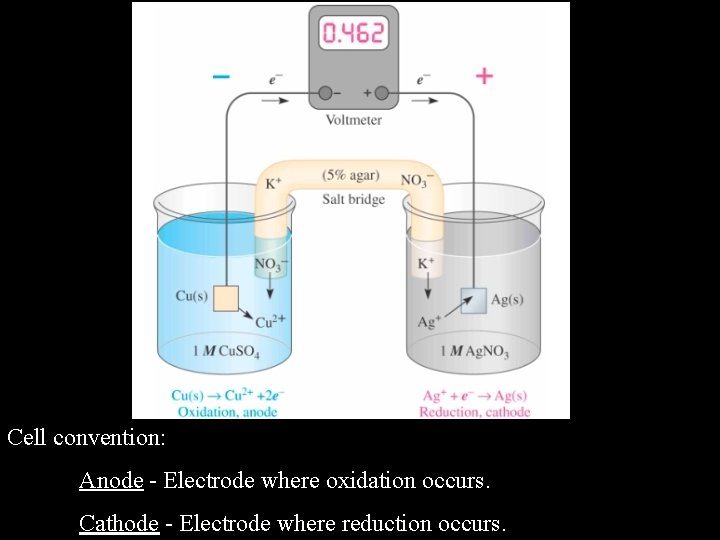
Cell convention: Anode - Electrode where oxidation occurs. Cathode - Electrode where reduction occurs.

Cell Notation It is convenient to have a method for indicating the elements of a galvanic cell. This is done as follows: 1) List the elements of the cell, in order, from the anode (left) to the cathode (right). 2) Use a single vertical line to indicate a change in phase. 3) Use a double vertical line to indicate a salt bridge. We can also indicate the concentration or partial pressure of substances in the galvanic cell for cases where that information is useful.

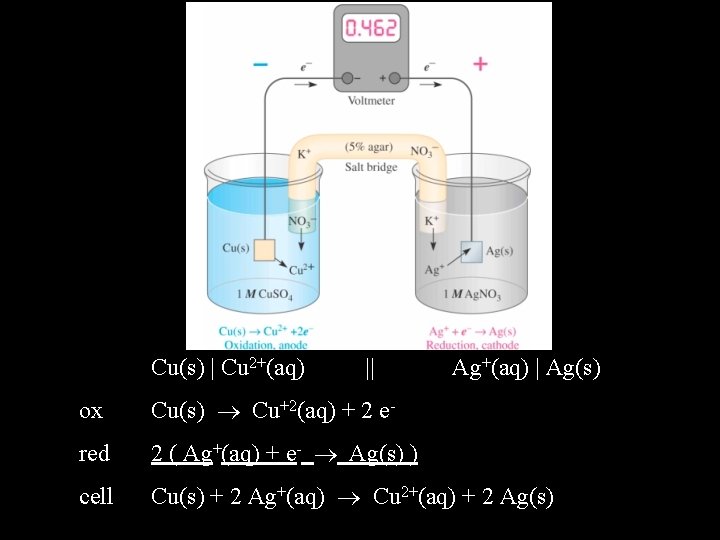
Cu(s) | Cu 2+(aq) || Ag+(aq) | Ag(s) ox Cu(s) Cu+2(aq) + 2 e- red 2 ( Ag+(aq) + e- Ag(s) ) cell Cu(s) + 2 Ag+(aq) Cu 2+(aq) + 2 Ag(s)

Example: Give the half-cell oxidation reaction, the half cell reduction reaction, and the net cell reaction for the galvanic cells with the following shorthand notation. Zn(s) | Zn 2+(aq) || Cu 2+(aq) | Cu Pt(s) | H 2(g) | H+(aq) || Cl-(aq) | Ag. Cl(s) | Ag(s)

Zn(s) | Zn 2+(aq) || Cu 2+(aq) | Cu anode cathode ox Zn(s) Zn 2+(aq) + 2 e- red Cu 2+(aq) + 2 e- Cu(s) cell Zn(s) + Cu 2+(aq) Zn 2+(aq) + Cu(s)

Pt(s) | H 2(g) | H+(aq) || Cl-(aq) | Ag. Cl(s) | Ag(s) anode cathode ox H 2(g) 2 H+(aq) + 2 e- red 2 ( Ag. Cl(s) + e- Ag(s) + Cl-(aq) ) cell H 2(g) + 2 Ag. Cl(s) 2 Ag(s) + 2 H+(aq) + 2 Cl-(aq) Standard hydrogen electrode (SHE) - Electrode where the following process takes place (either as an oxidation or as a reduction half reaction). ox H 2(g) 2 H+(aq) + 2 e- red 2 H+(aq) + 2 e- H 2(g) Platinum is used as the electrode since it is chemically inert.

Standard Cell Potential The standard half-cell potential (E ) is the voltage generated by a half-cell reaction. We can talk about either a standard half-cell reduction potential (E red) or a standard half-cell oxidation potential (E ox) which correspond to the potential generated by these processes when all reactants and products are present at standard concentration. Since galvanic cells must have both an oxidation and a reduction half-cell reaction, the standard half-cell reduction potential is defined relative to the potential generated by the standard hydrogen electrode (SHE). 2 H+(aq) + 2 e- H 2(g) E red = 0. 00 v (by definition) H 2(g) 2 H+(aq) + 2 e- E ox = 0. 00 v Based on this definition experimental values for other half-cell reduction potentials can be found.

Example: Consider the following galvanic cell. Pt(s) | H 2(g) | H+(aq) || Cu 2+(aq) | Cu(s) The experimental value for the cell potential is E cell = 0. 34 v.

Example: Consider the following galvanic cell. Pt(s) | H 2(g) | H+(aq) || Cu 2+(aq) | Cu(s) ox H 2(g) 2 H+(aq) + 2 e- E ox red Cu 2+(aq) + 2 e- Cu(s) E red cell H 2(g) + Cu 2+(aq) 2 H+(aq) + Cu(s) E cell The experimental value for the cell potential is E cell = 0. 34 v. Since E cell = E ox + E red = E cell - E ox = 0. 34 v - 0. 00 v = 0. 34 v All half-cell reduction potentials can be found by the use of this method. A table of half-cell reduction potentials is found in Table 18. 1

Half-Cell Reduction Potentials (Table)

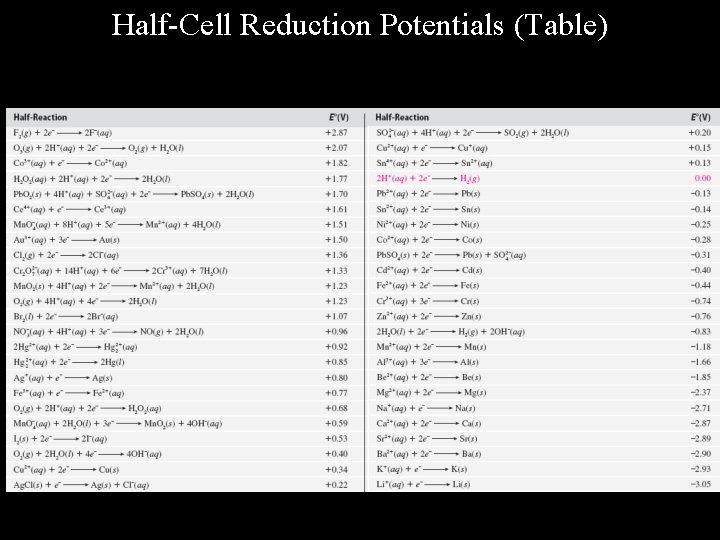
Half-Cell Reduction Potentials (Table)

Properties of Half-Cell Potentials 1) Reversing the direction of the reaction (changing the reaction from a reduction to an oxidation) changes the sign of the potential. Cu 2+(aq) + 2 e- Cu(s) E red = 0. 34 v Cu(s) Cu 2+(aq) + 2 e- E ox = - 0. 34 v 2) Multiplying a reaction by a positive constant has no effect on the value of the half-cell potential. This is because the potential is defined as that found for standard conditions. Cu 2+(aq) + 2 e- Cu(s) E red = 0. 34 v 2 Cu 2+(aq) + 4 e- 2 Cu(s) E red = 0. 34 v

Finding Cell Potentials For Standard Conditions The standard cell potential for a galvanic cell can be found by adding together the half-cell oxidation potential and the half-cell reduction potential. Example: Zn(s) | Zn 2+(aq) || Cu 2+(aq) | Cu

Finding Cell Potentials For Standard Conditions Example: Zn(s) | Zn 2+(aq) || Cu 2+(aq) | Cu ox Zn(s) Zn 2+(aq) + 2 e- E ox = 0. 76 v red Cu 2+(aq) + 2 e- Cu(s) E red = 0. 34 v cell Zn(s) + Cu 2+(aq) Zn 2+(aq) + Cu(s) E cell = 1. 10 v Because half-cell oxidation potentials can be found from half-cell reduction potentials (by reversing the direction of the reaction and the sign of the potential) we typically only keep tables of the half-cell reduction potentials.

Free Energy and Cell Potential The connection between galvanic cells and thermodynamics is through the following relationship (which can be derived). Grxn = - n F Ecell G rxn = - n F E cell In the above expressions n is the number of electrons transferred per mole of reaction (which can be found from either the oxidation or the reduction half-cell reaction) and F is the Faraday constant, a conversion factor between Coulombs (MKS unit of charge) and moles of charge. F = 96485 C/mol Note (1 volt) (1 Coulomb) = 1 Joule In the previous galvanic cell n = 2 and E cell = 1. 10 v, so G rxn = - (2) (96485 C/mol) (1. 10 v) = - 212. 3 k. J/mol (spontaneous)

Spontaneous Cell Reactions Based on the above results we can determine when a cell reaction will occur spontaneously. Since Grxn = - n F Ecell we have the following possibilities Ecell > 0 means Grxn < 0 and the reaction is spontaneous Ecell = 0 means Grxn = 0 and the system is at equilibrium Ecell < 0 means Grxn > 0 and the reaction is not spontaneous Note that in the last case the reverse reaction will be spontaneous (a consequence of free energy being a state function). Since the above is true in general it is also true for cells where standard conditions (so true if we add “ ” to Grxn and Ecell in the above expressions.

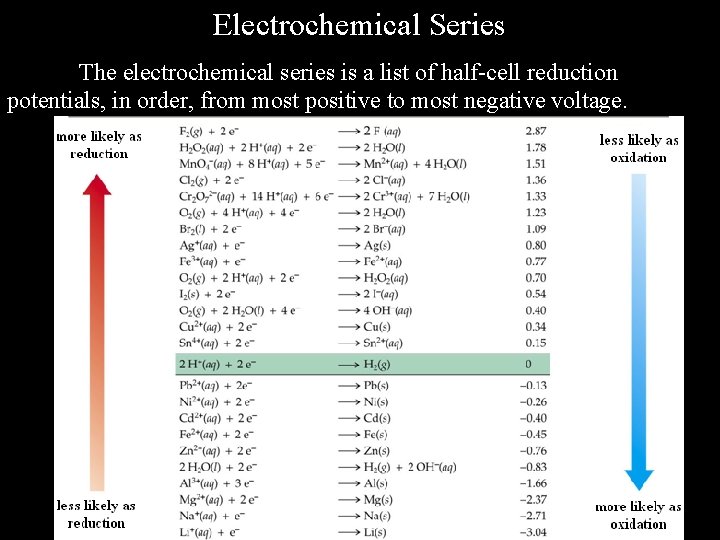
Electrochemical Series The electrochemical series is a list of half-cell reduction potentials, in order, from most positive to most negative voltage.

Properties of the Electrochemical Series Since reactions where E cell is positive are spontaneous, we may say the more positive a half-cell potential the more likely it will lead to a spontaneous cell reaction. That means that reactions at the top of the series are most likely to occur as reduction reactions, and reactions at the bottom of the series are least likely to occur as reduction reactions. Because changing from a reduction to an oxidation reaction changes the sign of the half-cell potential, it also means that reactions at the bottom of the series are most likely to occur as oxidation reactions, and reactions at the top of the series are least likely to occur as oxidation reactions. Example: Which of the following reactions will occur spontaneously for standard conditions? Ni 2+(aq) + Zn(s) Ni(s) + Zn 2+(aq) + Ni(s) Zn(s) + Ni 2+(aq)

Example: Which of the following reactions will occur spontaneously for standard conditions? Ni 2+(aq) + Zn(s) Ni(s) + Zn 2+(aq) + Ni(s) Zn(s) + Ni 2+(aq) In the first reaction Ni 2+ is an oxidizing agent, while in the second reaction Zn 2+ is an oxidizing agent. Based on the above portion of the electrochemical series Ni 2+ is more likely to be reduced than Zn 2+, and so it is the first reaction that will be spontaneous (in fact E cell = + 0. 50 v for the first process and – 0. 50 v for the second process).

The Nernst Equation The central equation for galvanic cells is the Nernst equation. It may be derived in the following manner. Recall the following thermochemical relationship Grxn = G rxn + RT ln Q However, we have a connection between free energy and cell potential Grxn = - n F Ecell If we use the above to substitute, we get - n F Ecell = - n F E cell + RT ln Q Ecell = E cell – RT ln Q n. F the Nernst equation.

Uses of the Nernst Equation The Nernst equation can be used to predict the value for the cell potential for cases where reactants and products are not at their standard concentrations. Example: Consider the following galvanic cell Zn(s) | Zn 2+(aq, 0. 010 M) || Cu 2+(aq, 1. 00 M) | Cu What is Ecell for the above galvanic cell?

Zn(s) | Zn+2(aq, 0. 010 M) || Cu 2+(aq, 1. 00 M) | Cu What is Ecell for the above galvanic cell? From the Nernst equation Ecell = E cell – RT ln Q n. F ox Zn(s) Zn 2+(aq) + 2 ered Cu 2+(aq) + 2 e- Cu(s) cell Zn(s) + Cu 2+(aq) Zn 2+(aq) + Cu(s) E ox = 0. 76 v E red = 0. 34 v E cell = 1. 10 v n = 2 Q = [Zn 2+] = (0. 010) = 0. 010 [Cu 2+] (1. 00) So Ecell = 1. 10 v – (8. 314 J/mol. K) (298. 2 K) ln(0. 010) (2) (96485 C/mol) = 1. 10 v + 0. 059 v = 1. 16 v

The Nernst Equation and Equilibrium The Nernst equation says Ecell = E cell – RT ln Q n. F Consider a system at equilibrium. In this case Grxn = 0, which means Ecell = 0, and Q = K, the equilibrium constant. If we substitute this into the Nernst equation we get 0 = E cell – RT ln K n. F E cell = RT ln K n. F ln K = n F E cell RT Using this expression we can obtain values for the equilibrium constant for any reaction that can be represented by a galvanic cell.

Example: The solubility product for silver chloride (Ag. Cl) is Ksp = [Ag+][Cl-]. Use data for half-cell reduction potentials to find a numerical value for Ksp.

Example: The solubility product for silver chloride (Ag. Cl) is Ksp = [Ag+] [Cl-]. Use data for half-cell reduction potentials to find a numerical value for Ksp. The solubility product reaction is Ag. Cl(s) Ag+(aq) + Cl-(aq) ox Ag(s) Ag+(aq) + e- E ox = - 0. 80 v red Ag. Cl(s) + e- Ag(s) + Cl- E red = + 0. 22 v cell Ag. Cl(s) Ag+(aq) + Cl-(aq) E cell = - 0. 58 v So ln K = n F E cell = (1) (96485 C/mol) (- 0. 58 v) = - 22. 57 RT (8. 314 J/mol. K) (298. 2 K) Ksp = e-22. 57 = 1. 6 x 10 -10

Electrochemical Determination of p. H We may construct a galvanic cell that allows us to measure p. H based on an electrochemical measurement. H 2(g) | H+(aq, MH+) || “reference electrode” where “reference electrode” refers to a cathode that will give a stable value for E red, and MH+ is the concentration of hydrogen ion for the anode solution (the solution whose p. H we wish to determine). Note that our anode is the standard hydrogen electrode (SHE) except that the 1. 0 M H+ solution has been replaced by the solution whose p. H we wish to determine.

ox H 2(g) 2 H+(aq) + 2 e- E ox = 0. 00 v red “reference electrode” E red cell E cell = E red Ecell = E cell - RT ln Q n = 2 ; Q = [H+]2/(p. H 2) n. F = E red - (8. 314 J/mol. K) (298. 2 K) ln{([H+]2/(p. H 2)} (2) (96485 C/mol) For p. H 2 = 1. 00 atm, this becomes Ecell = E red - (0. 0256 v) ln[H+] = E red + (0. 0256 v) { - ln[H+]} = E red + (0. 0592 v) { - log 10[H+]} = E red + (0. 0592 v) p. H

If we solve this for p. H, we get Ecell = E red + (0. 0592 v) p. H (Ecell - E red) = (0. 0592 v) p. H = (Ecell - E red)/(0. 0592 v) What this means is that by measuring a cell potential for an appropriate galvanic cell we can find the p. H of a solution. To measure p. H to a precision of 0. 03 p. H units requires a precision in measuring voltage of (0. 03) (0. 0592 v) 0. 002 v, not a difficult thing to do. In practice, because of the complexity of the standard hydrogen electrode we usually use other types of electrodes in p. H measurements, such as the glass-calomel electrode.

Lead Storage Battery The lead storage battery is typically used as a car battery because it is rugged, reliable, rechargable, and capable of storing a large amount of electrical energy. The cell reactions are as follows ox Pb(s) + HSO 4 -(aq) Pb. SO 4(s) + H+(aq) + 2 e- 0. 296 v red Pb. O 2(s) + 3 H+(aq) + HSO 4 -(aq) + 2 e Pb. SO 4(s) + 2 H 2 O( ) 1. 628 v cell Pb(s) + Pb. O 2(s) + 2 H+(aq) + 2 HSO 4 -(aq) 2 Pb. SO 4(s) + 2 H 2 O( ) 1. 924 v

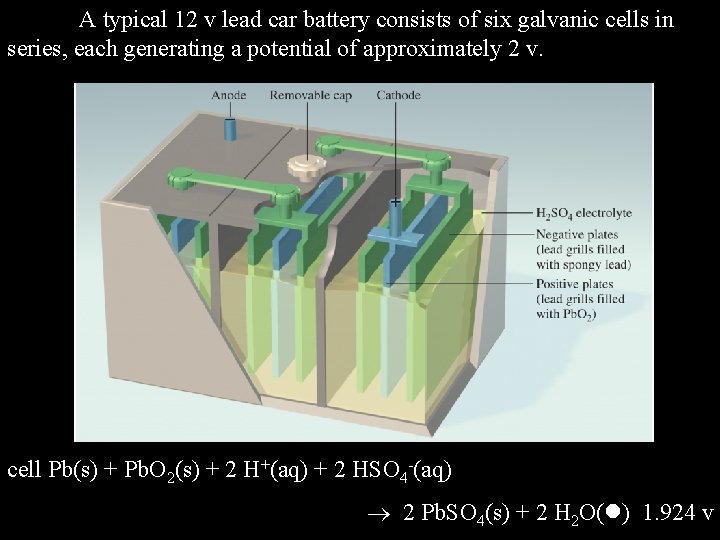
A typical 12 v lead car battery consists of six galvanic cells in series, each generating a potential of approximately 2 v. cell Pb(s) + Pb. O 2(s) + 2 H+(aq) + 2 HSO 4 -(aq) 2 Pb. SO 4(s) + 2 H 2 O( ) 1. 924 v

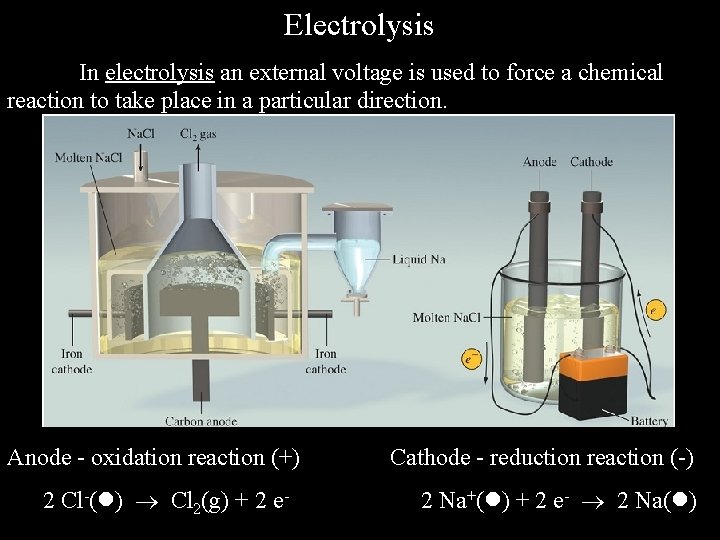
Electrolysis In electrolysis an external voltage is used to force a chemical reaction to take place in a particular direction. Anode - oxidation reaction (+) 2 Cl-( ) Cl 2(g) + 2 e- Cathode - reduction reaction (-) 2 Na+( ) + 2 e- 2 Na( )

As in galvanic cells, we can write down the half-cell oxidation and reduction reactions and the net cell reactions for an electrolytic cell. ox 2 Cl-( ) Cl 2(g) + 2 e- red 2 ( Na+( ) + e- Na( ) ) cell 2 Na+( ) + 2 Cl-( ) 2 Na( ) + Cl 2(g) Notice that in electrolysis the reactions that take place are opposite of those that would normally occur. The Nernst equation does not apply for electrolysis, since we are not generating a voltage in an electrolytic cell. All that is required is that the external voltage being used is large enough to drive the reaction in the desired direction.

Identifying the Species Being Oxidized or Reduced In an electrolytic cell the species involved in the reactions are usually the ones that require the most positive (least negative) voltage to be oxidized or reduced. We can use the electrolytic series to identify which substances this will be. Example: Consider the electrolysis of aqueous sodium chloride (Na. Cl(aq)). What oxidation and reduction reactions will occur?

Example: Consider the electrolysis of aqueous sodium chloride (Na. Cl(aq)). What oxidation and reduction reactions will occur? red ox Na+(aq) + e- Na(s) E = - 2. 71 v 2 H 2 O(l) + 2 e- H 2(g) + 2 OH-(aq) E = - 0. 83 v 2 Cl-(aq) Cl 2(g) + 2 e- E = - 1. 36 v 2 H 2 O(l) O 2(g) + 4 H+(aq) + 4 e- E = - 1. 23 v Based on the above we would expect production of H 2(g) at the cathode, and production of O 2(g) at the anode. In fact, while H 2(g) is produced at the cathode, it is Cl 2(g), and not O 2(g) that forms at the anode. This is because for cases where the potentials for different possible reactions are close (within ~ 0. 5 v) there are other factors that come into play that may determine the reaction that occurs.

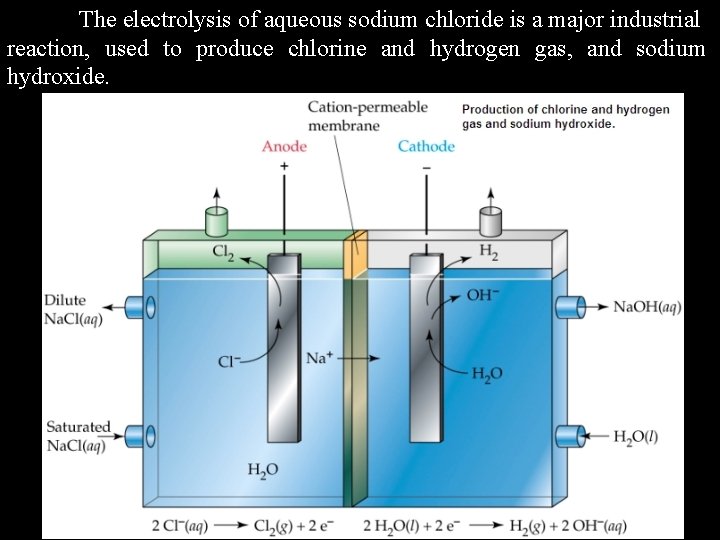
The electrolysis of aqueous sodium chloride is a major industrial reaction, used to produce chlorine and hydrogen gas, and sodium hydroxide.

Calculations Involving Electrolytic Cells The main type of calculation done in connection with electrolytic cells is finding the mass of a particular substance that can be produced in a particular cell, given the operating conditions. To do these calculations requires: 1) The appropriate half cell reaction. 2) The number of moles of electrical charge transferred. 3) The molecular mass of the product.

Example: Electrolysis is carried out for molten sodium chloride. The cell is operated at a current i = 20. 0 amp (1 amp = 1 C/s) for a period of 1. 00 hour. How many grams of Cl 2 (MW = 70. 90 g/mol) will be produced?

Electrolysis is carried out for molten sodium chloride. The cell is operated at a current i = 20. 0 amp (1 amp = 1 C/s) for a period of 1. 00 hour. How many grams of Cl 2 will be produced? 1) The appropriate half cell reaction. 2 Cl-(l) Cl 2(g) + 2 e 2) The number of moles of electrical charge transferred. mol charge = 1. 00 hr 3600 s 20. 0 C 1 hr s 1 mol = 0. 746 mol 96485 C 3) The molecular mass of the product. M(Cl 2) = 70. 90 g/mol. g Cl 2 = 0. 746 mol charge 1 mol Cl 2 2 mol charge 70. 90 g Cl 2 = 26. 5 g mol Cl 2

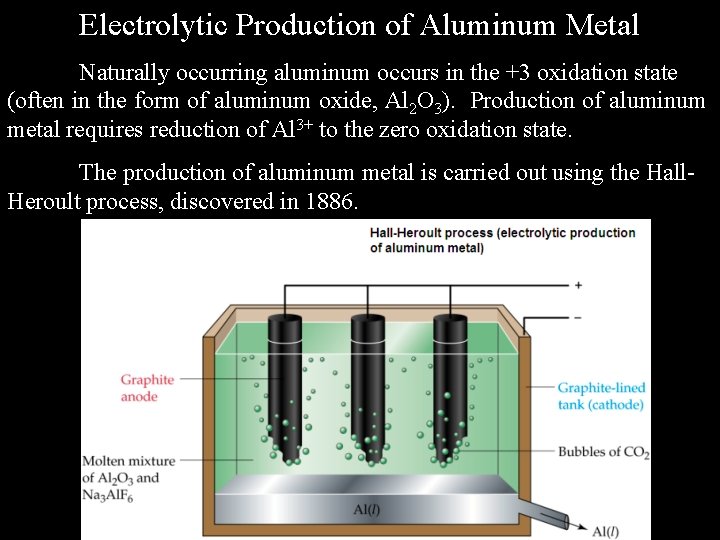
Electrolytic Production of Aluminum Metal Naturally occurring aluminum occurs in the +3 oxidation state (often in the form of aluminum oxide, Al 2 O 3). Production of aluminum metal requires reduction of Al 3+ to the zero oxidation state. The production of aluminum metal is carried out using the Hall. Heroult process, discovered in 1886.

How many moles and coulombs of electrons are required to produce 1. 00 kg of aluminum metal? (MW(Al) = 27. 0 g/mol)

How many moles and coulombs of electrons are required to produce 1. 00 kg of aluminum metal? (MW(Al) = 27. 0 g/mol) Al 3+ + 3 e- Al mol e- = 1000. g Al 1 mol Al 3 mol e- = 111. 1 mol e- 27. 0 g Al 1 mol Al coulombs e- = 111. 1 mol e- 96485 C = 1. 07 x 107 C mol It takes a substantial amount of electrical power to produce aluminum metal. In fact, 3% of the electrical power generated in the United States goes into the production of aluminum (an average of 15 kilowatt hours per kilogram of aluminum produced). This is one reason why recycling of aluminum products makes economic sense (production of recycled aluminum uses only 5% of the electricity used to produce aluminum from ore).

Corrosion is the general term given for the deterioration of metals by oxidation. The reduction of oxygen in corrosion is the process O 2(g) + 4 H+(aq) + 4 e- 2 H 2 O( )

Because the reduction potential for O 2(g) is large and positive, oxygen is expected to oxidize most metals, including copper, lead, nickel, iron, zinc, and aluminum. Some metals, like zinc and aluminum, develop a protective oxide coat (Zn. O; Al 2 O 3) that prevents further oxidation from taking place. The oxides for other metals, such as iron, are porous, and so the metals can oxidize until completely rusted through.

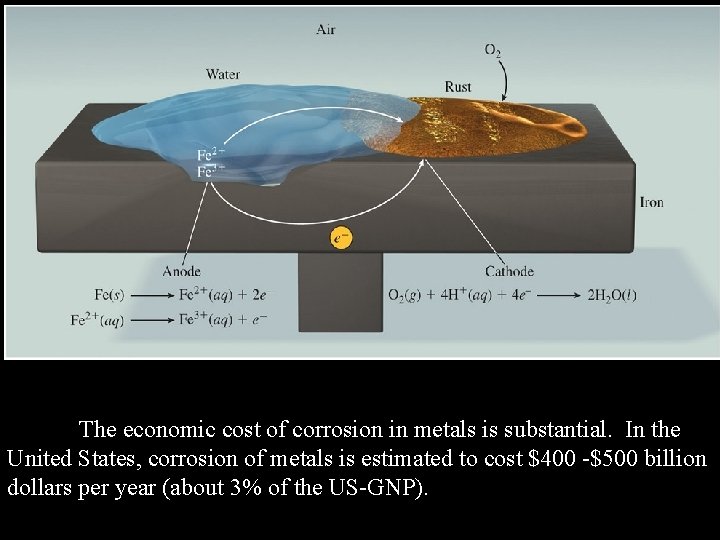
The economic cost of corrosion in metals is substantial. In the United States, corrosion of metals is estimated to cost $400 -$500 billion dollars per year (about 3% of the US-GNP).

End of Chapter 18 “Anode comes from the Greek (upward) and (a way), and therefore suggests the rising of the sun in the east. Cathode comes from (downward), and is related to the setting of the sun, in the west. ” - Keith Laidler, in The World of Physical Chemistry, explaining how Michael Faraday came up with the terms “anode” and “cathode”. “Rust never sleeps. ” - Neil Young (borrowed from Devo)