Chapter 18 Central Limit Theorem Dice simulator http

  • Slides: 13
Download presentation
Chapter 18 – Central Limit Theorem

Chapter 18 – Central Limit Theorem

Dice simulator �http: //www. stat. sc. edu/~west/javahtml/CLT. html �Let’s roll a single die a

Dice simulator �http: //www. stat. sc. edu/~west/javahtml/CLT. html �Let’s roll a single die a few times and see what happens �What do you think would happen if we rolled 2 dice? Would we expect the same distribution? �Now let’s try 3 dice and then 5 dice

NFL Data �Minitab data set

NFL Data �Minitab data set

Sampling Distribution of a Mean �Rolling dice simulation � 10, 000 individual rolls recorded

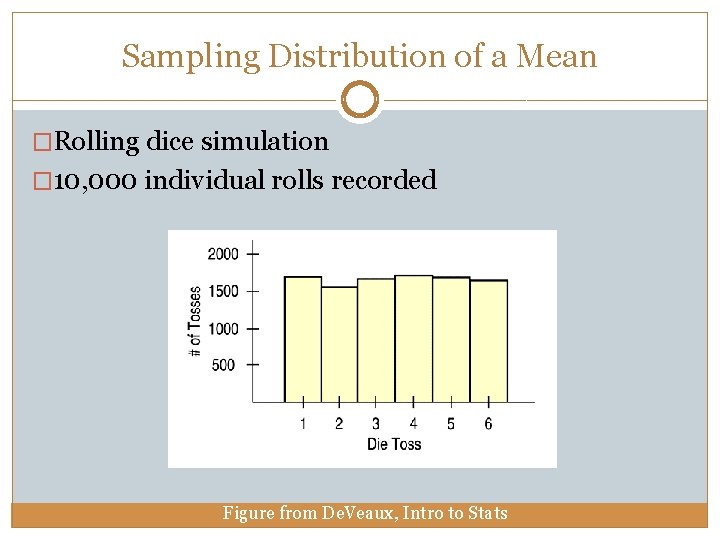
Sampling Distribution of a Mean �Rolling dice simulation � 10, 000 individual rolls recorded Figure from De. Veaux, Intro to Stats

Sampling Distribution of a Mean �Roll 2 dice 10, 000 times, average the 2

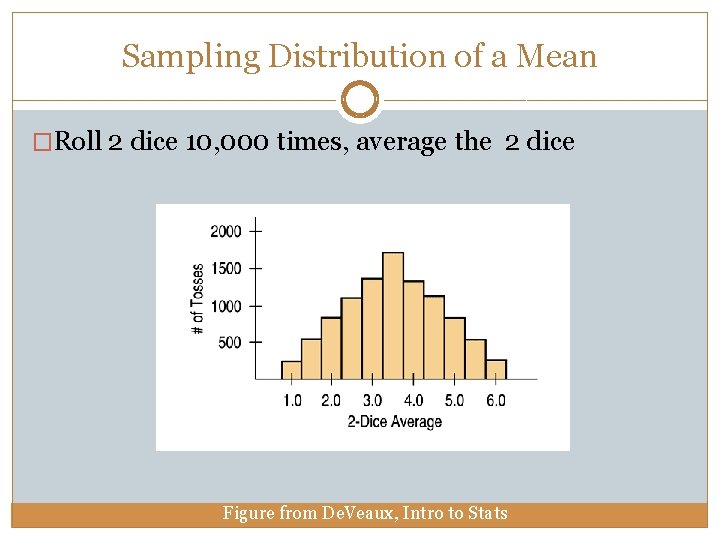
Sampling Distribution of a Mean �Roll 2 dice 10, 000 times, average the 2 dice Figure from De. Veaux, Intro to Stats

Sampling Distribution of a Mean �Rolling 3 dice 10, 000 times and averaging the

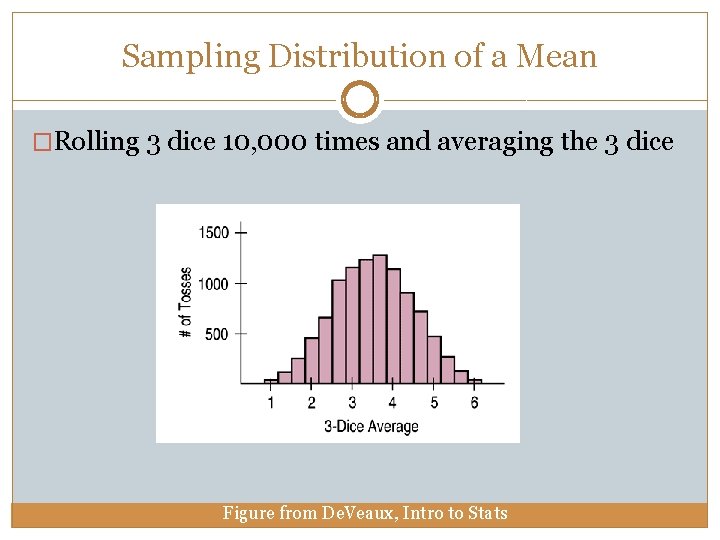
Sampling Distribution of a Mean �Rolling 3 dice 10, 000 times and averaging the 3 dice Figure from De. Veaux, Intro to Stats

Sampling Distribution of a Mean �Rolling 5 dice 10, 000 times and averaging Figure

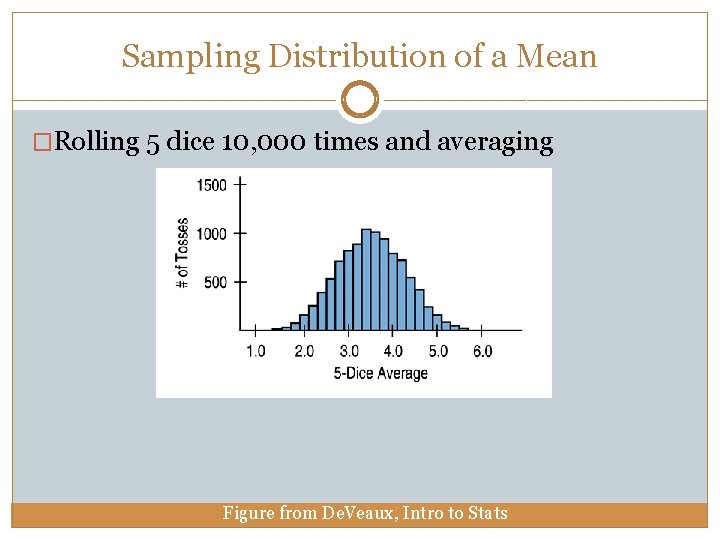
Sampling Distribution of a Mean �Rolling 5 dice 10, 000 times and averaging Figure from De. Veaux, Intro to Stats

Sampling Distribution of a Mean �Rolling 20 dice 10, 000 times and averaging �Once

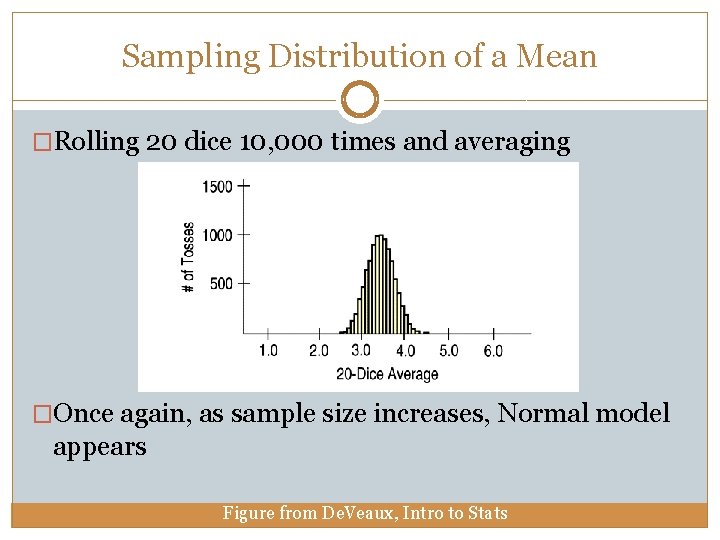
Sampling Distribution of a Mean �Rolling 20 dice 10, 000 times and averaging �Once again, as sample size increases, Normal model appears Figure from De. Veaux, Intro to Stats

Central Limit Theorem �The sampling distribution of any mean becomes more nearly Normal as

Central Limit Theorem �The sampling distribution of any mean becomes more nearly Normal as the sample size grows. The larger the sample, the better the approximation will be Doesn’t matter what the shape of the distribution of the population is! (uniform, symmetric, skewed…) �Observations need to be independent and collected with randomization.

CLT Assumptions �Assumptions: Independence: sampled values must be independent Sample Size: sample size must

CLT Assumptions �Assumptions: Independence: sampled values must be independent Sample Size: sample size must be large enough �Conditions: Randomization 10% Condition Large enough sample

Which Normal Model to use? �The Normal Model depends on a mean and sd

Which Normal Model to use? �The Normal Model depends on a mean and sd �Sampling Distribution Model for a Mean When a random sample is drawn from any population with mean µ and standard deviation σ, its sample mean y has a sampling distribution with: Mean: µ Standard Deviation:

Example: CEO compensation � 800 CEO’s �Mean (in thousands) = 10, 307. 31 �SD

Example: CEO compensation � 800 CEO’s �Mean (in thousands) = 10, 307. 31 �SD (in thousands) = 17, 964. 62 �Samples of size 50 were drawn with: �Mean = 10, 343. 93 SD = 2, 483. 84 �Samples of size 100 were drawn with: �Mean = 10, 329. 94 SD = 1, 779. 18 �According to CLT, what should theoretical mean and sd be? Example from De. Veaux, Intro to Stats

Normal Models �Binomial µ = np σ= �Sampling distribution for proportions �Sampling distribution for

Normal Models �Binomial µ = np σ= �Sampling distribution for proportions �Sampling distribution for means SD(y) =

Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central Limit Theorem The central limit theorem andCentral Limit Theorem The central limit theorem and
Central limit theorem outlines Central limit theorem CLTCentral limit theorem outlines Central limit theorem CLT
Central limit theorem revisited Throw a dice twelveCentral limit theorem revisited Throw a dice twelve
Central Limit Theorem The theorem states that theCentral Limit Theorem The theorem states that the
LIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSILIMIT FUNGSI ALJABAR Limit fungsi aljabar LIMIT FUNGSI
Limit Sets Limit Sets Defined Limit Sets groupsLimit Sets Limit Sets Defined Limit Sets groups
LIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsiLIMIT FUNGSI LIMIT FUNGSI PENGERTIAN LIMIT Perhatikan fungsi
Limit MATHEMATICS LIMIT CRASH COURSE Limit of aLimit MATHEMATICS LIMIT CRASH COURSE Limit of a
limit Limit f limit f 0limit f xlimit Limit f limit f 0limit f x
Central Limit Theorem l Sampling Distributions l CentralCentral Limit Theorem l Sampling Distributions l Central
Ch 7 Central Limit Theorem Use the CentralCh 7 Central Limit Theorem Use the Central