Chapter 18 2 Concentration v time graphs Objectives

Chapter 18. 2 Concentration v time graphs

Objectives 1. From a concentration – time graph be able to : (i) Deduce the order (which will be 0 or 1 st) with respect to a reactant from the shape of the graph (ii) Calculate the reaction rate from the measurement of gradients 2. From a concentration–time graph of a first order reaction be able to measure a constant half-life, denoted by t 1/2 3. For a first order reaction determine the rate constant, k, from the constant half-life, t ½ , using the relationship : k = ln 2 / t 1/2

https: //www. youtube. com/watch? v=tf 1 P 6 Cj. Qik. I 1. Reminder of how to carry out an experiment to monitor the rate of a reaction by gas collection https: //www. youtube. com/watch? v=Cxx. Giqa. BEPs 2. Using a colorimeter This method can be used when you have a coloured chemical like bromine or iodine or nitrogen dioxide that is being used up as a reactant or created as a product 3. If a gas is produced in a reaction the loss of mass can be monitored as the reaction proceeds

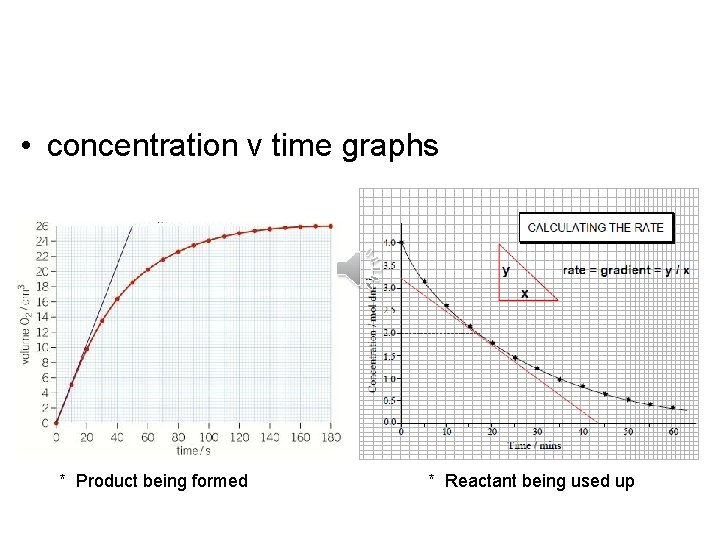
• concentration v time graphs * Product being formed * Reactant being used up

Half life of reactions • Let’s look specifically at : The concentration of a reactant being used up against time

A+B C+D Order with respect to A? [A] Time First

A+B C+D Order with respect to A? [A] Time Second

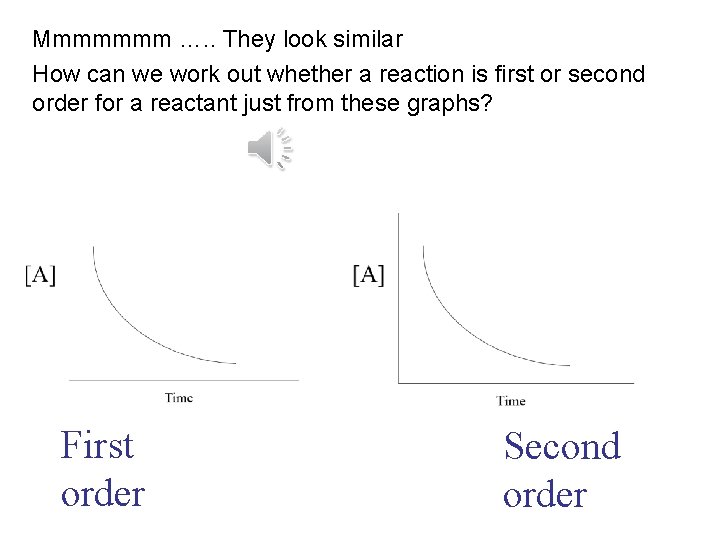
Mmmmmmm …. . They look similar How can we work out whether a reaction is first or second order for a reactant just from these graphs? First order Second order

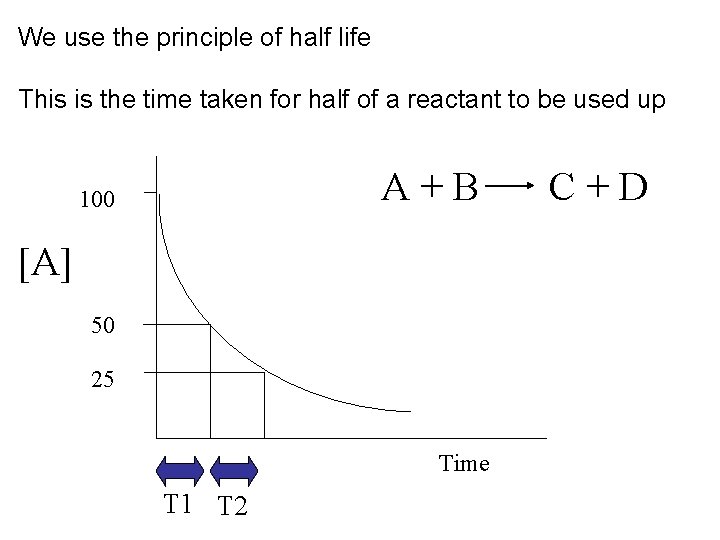
We use the principle of half life This is the time taken for half of a reactant to be used up A+B 100 [A] 50 25 Time T 1 T 2 C+D

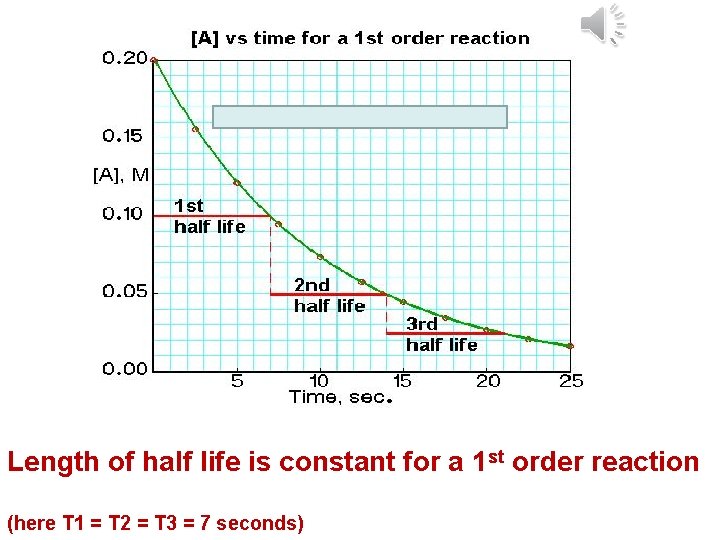
Length of half life is constant for a 1 st order reaction (here T 1 = T 2 = T 3 = 7 seconds)

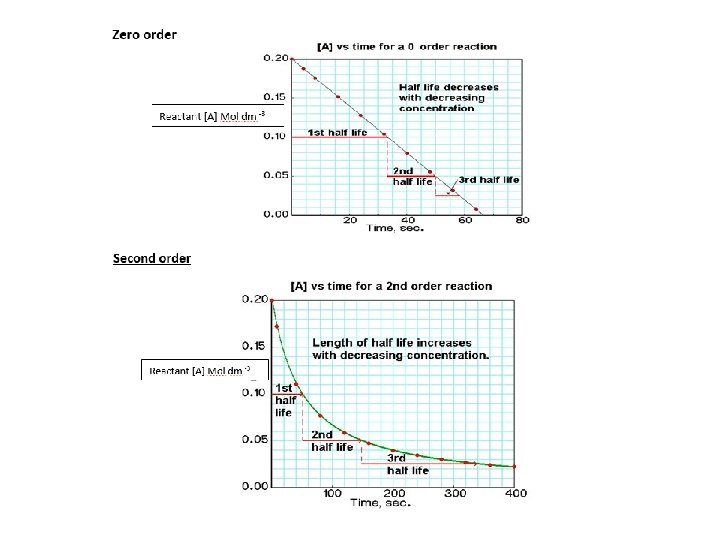
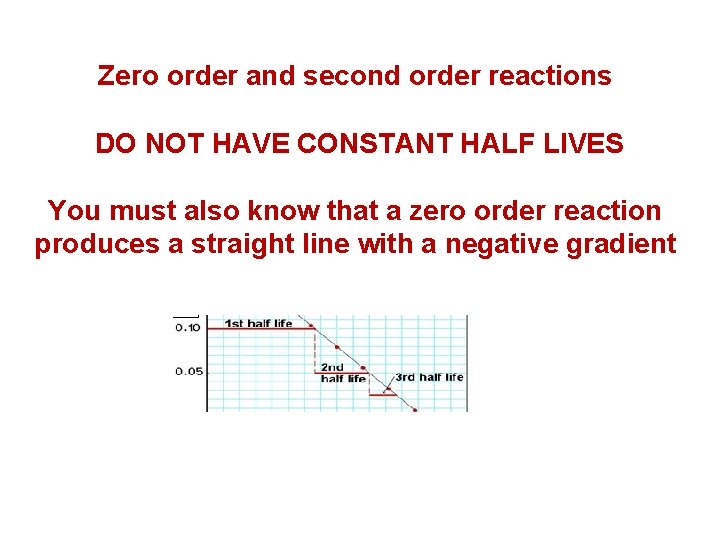
Zero order and second order reactions DO NOT HAVE CONSTANT HALF LIVES You must also know that a zero order reaction produces a straight line with a negative gradient

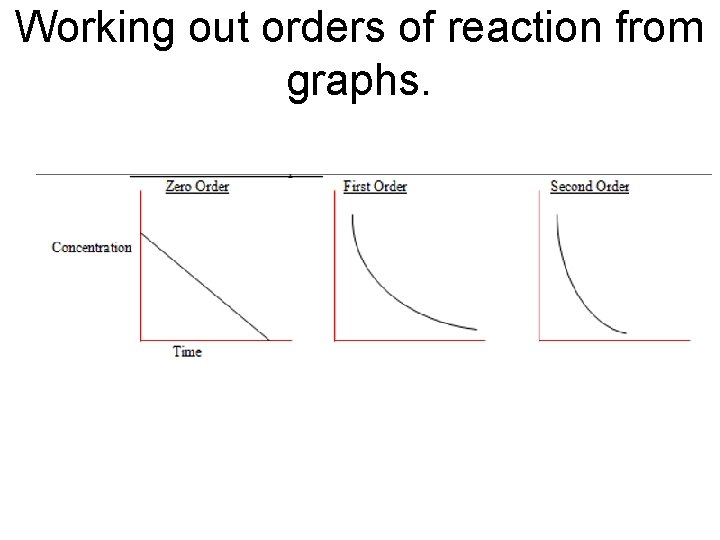
Working out orders of reaction from graphs.

2 methods to be familiar with • Calculating rate of reaction from gradient of tangent at a particular concentration or time • Calculating rate constant from half life using equation : k = ln 2 t 1/2

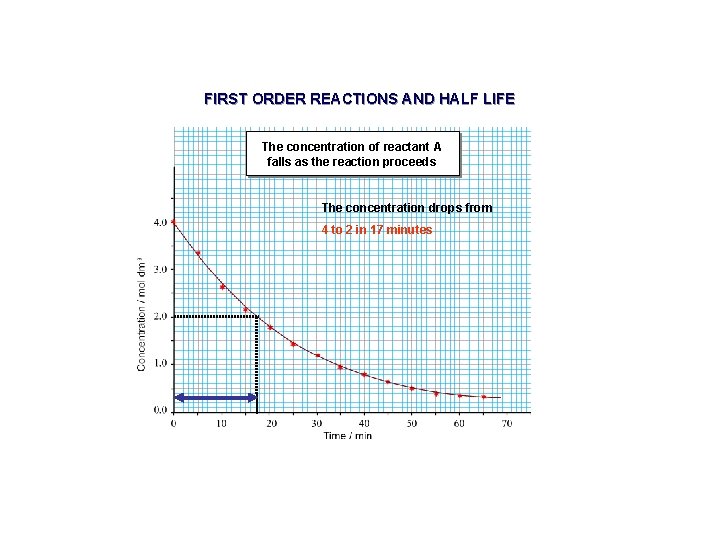
FIRST ORDER REACTIONS AND HALF LIFE The concentration of reactant A falls as the reaction proceeds The concentration drops from 4 to 2 in 17 minutes

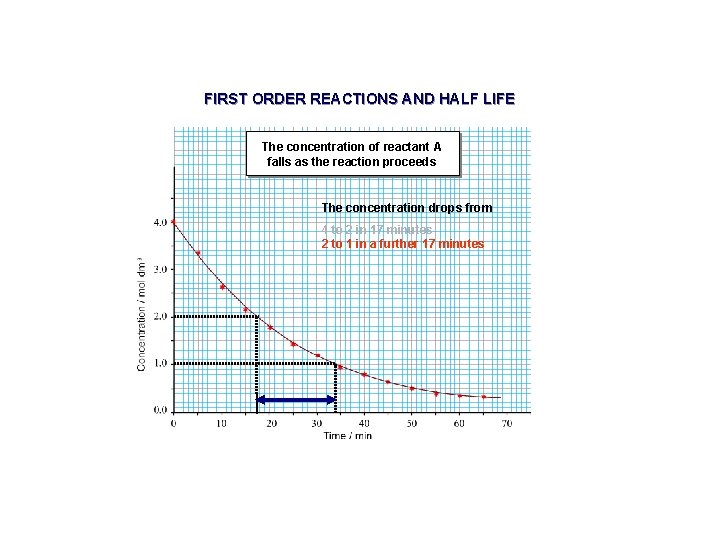
FIRST ORDER REACTIONS AND HALF LIFE The concentration of reactant A falls as the reaction proceeds The concentration drops from 4 to 2 in 17 minutes 2 to 1 in a further 17 minutes

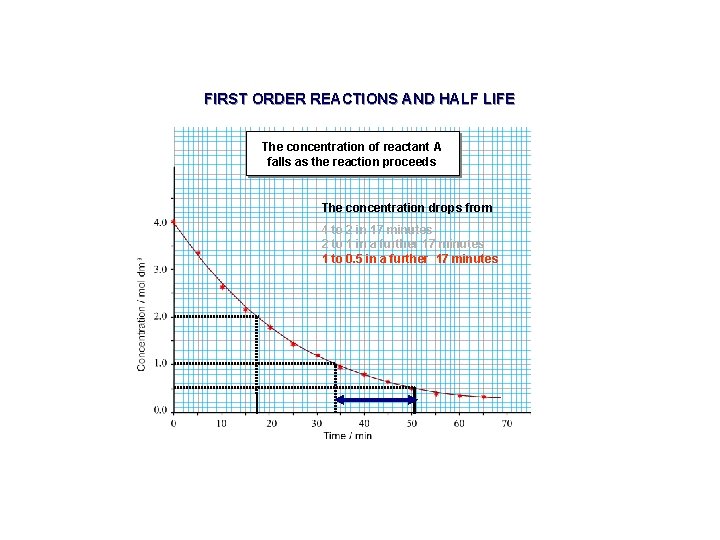
FIRST ORDER REACTIONS AND HALF LIFE The concentration of reactant A falls as the reaction proceeds The concentration drops from 4 to 2 in 17 minutes 2 to 1 in a further 17 minutes 1 to 0. 5 in a further 17 minutes

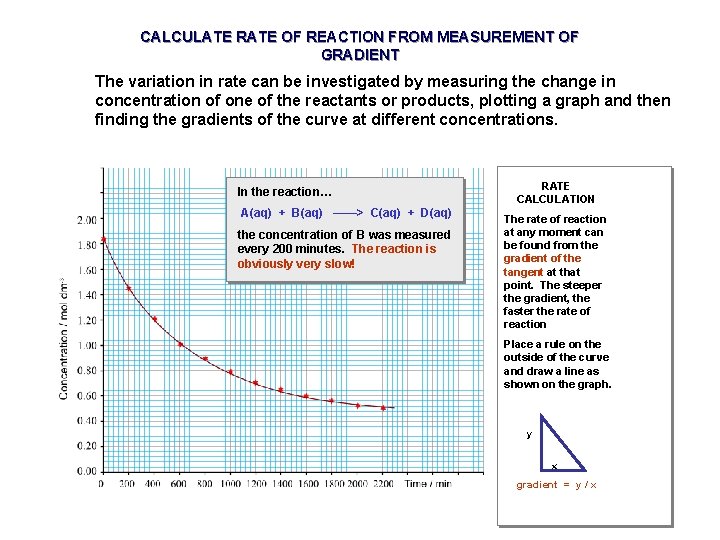
CALCULATE RATE OF REACTION FROM MEASUREMENT OF GRADIENT The variation in rate can be investigated by measuring the change in concentration of one of the reactants or products, plotting a graph and then finding the gradients of the curve at different concentrations. In the reaction… A(aq) + B(aq) ——> C(aq) + D(aq) the concentration of B was measured every 200 minutes. The reaction is obviously very slow! RATE CALCULATION The rate of reaction at any moment can be found from the gradient of the tangent at that point. The steeper the gradient, the faster the rate of reaction Place a rule on the outside of the curve and draw a line as shown on the graph. y x gradient = y / x

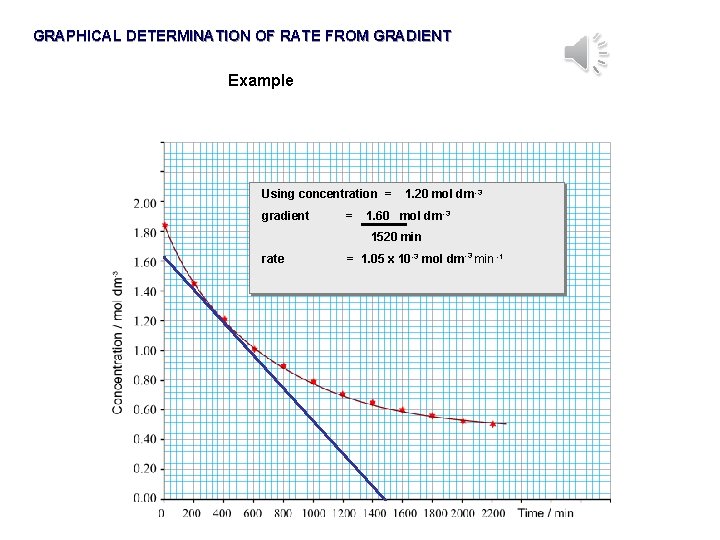
GRAPHICAL DETERMINATION OF RATE FROM GRADIENT Example Using concentration = gradient = 1. 20 mol dm -3 1. 60 mol dm -3 1520 min rate = 1. 05 x 10 -3 mol dm-3 min -1

DETERMINATION OF RATE CONSTANT (K) USING HALF LIFE If the reaction is first order the following relationship can be used, natural log of 2 divided by half life k = ln 2 t 1/2 This is a more accurate method to calculate k than trying to draw a tangent to a curve, calulate the gradient then substitute this into rate = k [A]

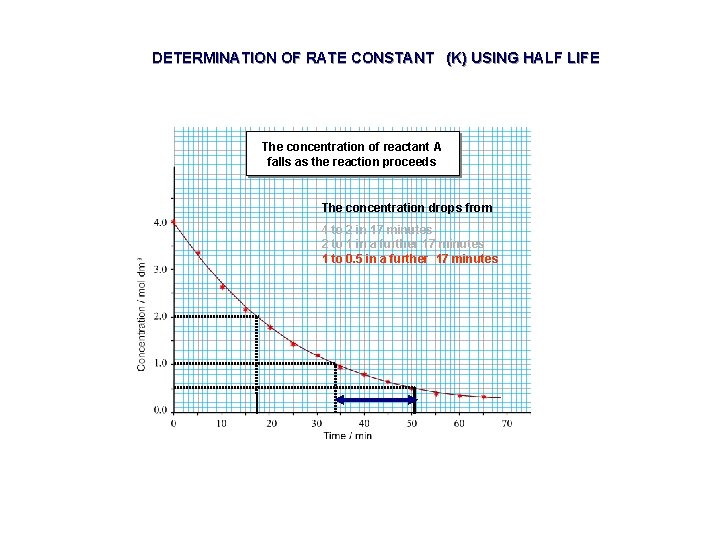
DETERMINATION OF RATE CONSTANT (K) USING HALF LIFE The concentration of reactant A falls as the reaction proceeds The concentration drops from 4 to 2 in 17 minutes 2 to 1 in a further 17 minutes 1 to 0. 5 in a further 17 minutes

DETERMINATION OF RATE CONSTANT (K) USING HALF LIFE If the reaction is first order the following relationship can be used, natural log of 2 divided by half life (the ln function is on your scientific calculator) k = ln 2 t 1/2 Using 17 mins as half life from previous slide this is 17 x 60 = 1020 seconds K = ln 2 1020 = 0. 693 1020 = 6. 80 x 10 -4 s -1

Now to put this into practice • Answer Q 1 2 3 and 4 on page 281 of the textbook and check your answers on p 574 • Then try the past paper question in the email