Chapter 17 Waves II Sound Waves Key contents

Chapter 17 Waves (II) Sound Waves

Key contents: Sound Waves Speed of Sound Pressure Fluctuation in Sound Waves Intensity and Sound Level Interference Sources of Musical Sound Beats Doppler Effect Supersonic Speeds, Shock Waves

Sound Waves Sound waves are longitudinal waves of density and pressure fluctuations. # In this chapter, we will focus on sound waves in the air. # For human ears, audible in 20 Hz ~ 20000 Hz

Speed of Sound l The wave speed on a string is l The bulk modulus B is defined to be the elastic factor for a gas: l With the density r being the inertia factor, the sound speed can be most likely expressed as

Speed of Sound A derivation: We have: Also, And Therefore, But Finally,

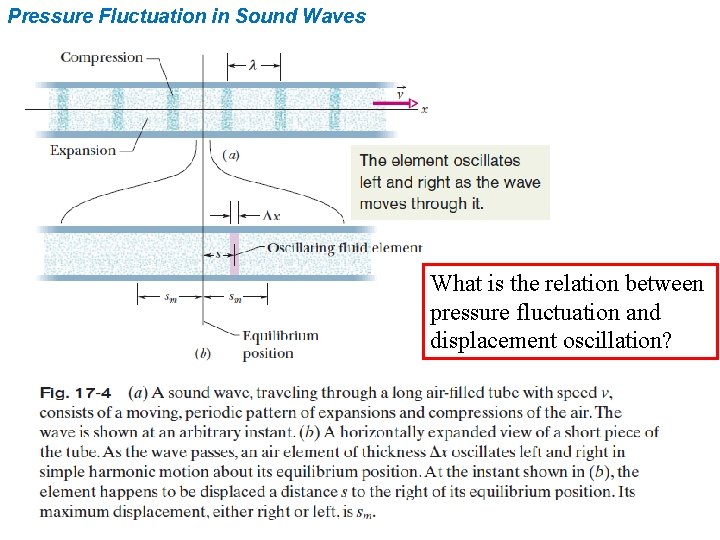
Pressure Fluctuation in Sound Waves What is the relation between pressure fluctuation and displacement oscillation?

Pressure Fluctuation in Sound Waves } # Δs is the displacement change at the two sides of the element Δx, while Δp is the pressure excess in Δx, and V=AΔx. # Δp and s are always with a 90 o phase difference. # From (the 1 st equality is the equation of motion), one may also see that

Example, Pressure and Displacement Amplitudes

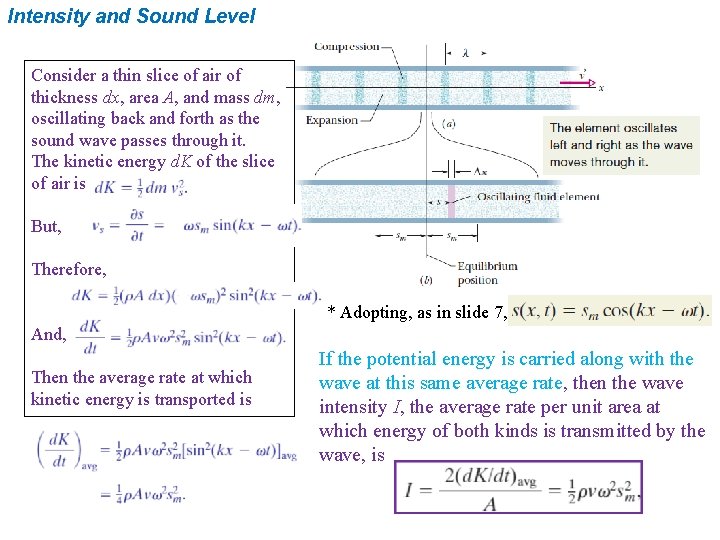
Intensity and Sound Level Consider a thin slice of air of thickness dx, area A, and mass dm, oscillating back and forth as the sound wave passes through it. The kinetic energy d. K of the slice of air is But, Therefore, * Adopting, as in slide 7, And, Then the average rate at which kinetic energy is transported is If the potential energy is carried along with the wave at this same average rate, then the wave intensity I, the average rate per unit area at which energy of both kinds is transmitted by the wave, is

Intensity and Sound Level Another derivation: The instantaneous power supplied to the wave element in the following figure is (p is the pressure excess) s (Note the different convention of using a sine function for s, and ) (recall ) This should be compared with that on a string:

Intensity and Sound Level The intensity I of a sound wave at a surface is the average rate per unit area at which energy is transferred by the wave through or onto the surface. Therefore, I =P/A where P is the time rate of energy transfer (the power) of the sound wave and A is the area of the surface intercepting the sound. The intensity I is related to the displacement amplitude sm of the sound wave by * Recall that in Ch 16 we have for a wave on a stretched string,

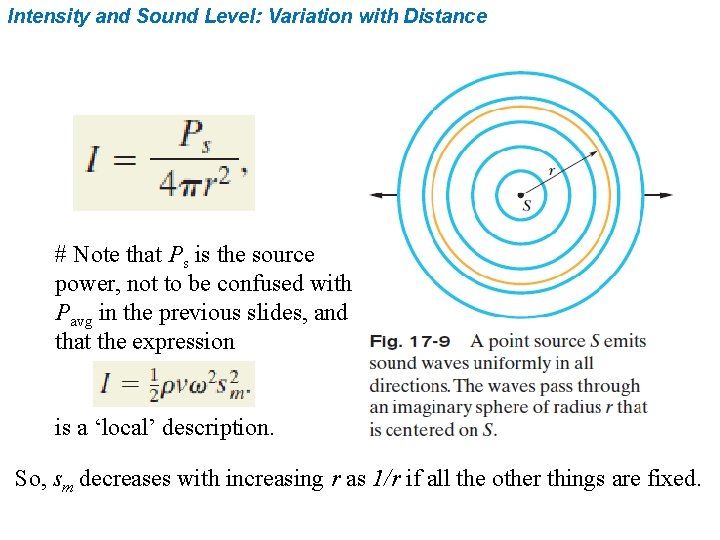
Intensity and Sound Level: Variation with Distance # Note that Ps is the source power, not to be confused with Pavg in the previous slides, and that the expression is a ‘local’ description. So, sm decreases with increasing r as 1/r if all the other things are fixed.

Intensity and Sound Level: The Decibel Scale Ex. For sound waves at 1 k. Hz in the air Here d. B is the abbreviation for decibel, the unit of sound level. (density is 1. 29 kg/m 3, sound speed 340 m/s) I 0 is a standard reference intensity ( 10 -12 W/m 2), chosen near the lower limit of the human range of hearing. @ 0 d. B, s 0 = 1. 07 x 10 -11 m p 0 = 2. 96 x 10 -5 Pa (1 atm = 1. 013 x 105 Pa) For I =I 0 , b =10 log 1 = 0, (our standard reference level corresponds to zero decibels). @ 120 d. B, s 0 = 1. 07 x 10 -5 m p 0 = 29. 6 Pa # office conversation, 60 d. B heavy traffic (3 m), 80 d. B loud rock music, 120 d. B Jet engine (20 m), 130 d. B (Recall that )

Example, Cylindrical Sound Wave:

Example, Decibel, Sound Level, Change in Intensity: Many veteran rockers suffer from acute hearing damage because of the high sound levels they endured for years while playing music near loudspeakers or listening to music on headphones. Recently, many rockers, began wearing special earplugs to protect their hearing during performances. If an earplug decreases the sound level of the sound waves by 20 d. B, what is the ratio of the final intensity If of the waves to their initial intensity Ii?

Interference

Interference Phase difference f can be related to path length difference DL, by noting that a phase difference of 2 p rad corresponds to one wavelength. Therefore, Fully constructive interference occurs when f is zero, 2 p, or any integer multiple of 2 p. Fully destructive interference occurs when f is an odd multiple of p:

Example, Interference:

Example, Interference:

Sources of Musical Sound Musical sounds can be set up by oscillating strings (guitar, piano, violin), membranes (kettledrum, snare drum), air columns (flute, oboe, pipe organ, and the digeridoo of Fig. 17 -12), wooden blocks or steel bars (marimba, xylophone), and many other oscillating bodies. Most common instruments involve more than a single oscillating part. Recall ‘standing waves’ in Ch 16.

Sources of Musical Sound A. Pipe open at both ends B. Pipe open at one end only

Example, Double Open and Single Open Pipes:

Beats When two sound waves whose frequencies are close, but not the same, are superimposed, a striking variation in the intensity of the resultant sound wave is heard. This is the beat phenomenon. The wavering of intensity occurs at a frequency which is the difference between the two combining frequencies.

Example, Beat Frequencies:

Doppler Effect When the motion of detector or source is toward the other, the sign on its speed must give an upward shift in frequency. When the motion of detector or source is away from the other, the sign on its speed must give a downward shift in frequency. Here the emitted frequency is f, the detected frequency is f’, v is the speed of sound through the air, v. D is the detector’s speed relative to the air, and v. S is the source’s speed relative to the air.

Example, Doppler Shift:

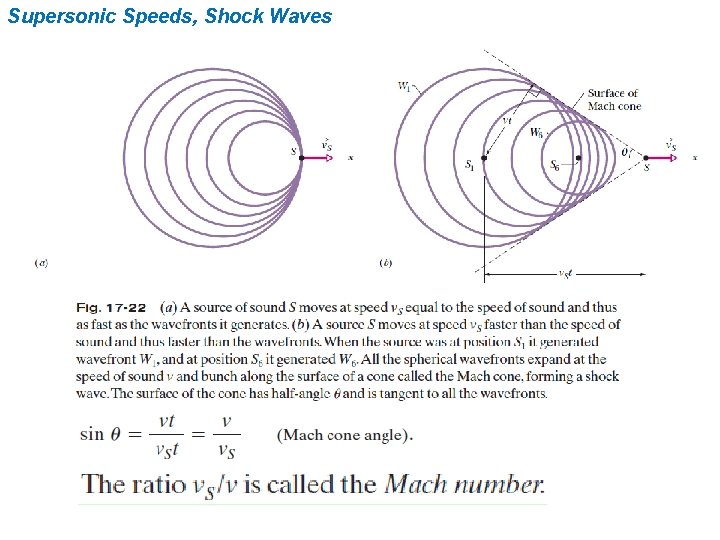
Supersonic Speeds, Shock Waves

Key contents: Sound Waves Speed of Sound Pressure Fluctuation in Sound Waves Intensity and Sound Level Interference Sources of Musical Sound Beats Doppler Effect Supersonic Speeds, Shock Waves