Chapter 17 Part B Inference about a Population

Chapter 17 Part B Inference about a Population Mean Match-Pair Samples Inference about µ 1

RECALL • Student’s t procedures are used to help infer population mean µ when population standard deviation σ not known • Characteristics of t densities similar to Standard Normal Z density but fatter tails based on df • Make sure you know the characteristics of the t density! William Sealy Gosset (“Student”) (1876– 1937) 2

Matched-Pairs Quantitative responses in matched pairs How do we handle data in which each data point in one sample is uniquely paired with a data point in the other sample? ANS: Maintain pairings, find their differences, and use the t procedure from the earlier part of the chapter on these differences! Inference about µ 3

Step 1 Statement Example: “Pollution” • We want to learn if pollution levels differ in two regions • Note: pollution levels vary daily depending on weather & other environmental conditions • Take pollution measures on 8 successive days in two regions (matched on “DAY”) • Consider these 8 measurement an SRS of pollution levels on all days at all times Inference about µ DAY 1 2 3 4 5 6 7 8 region A B 2. 92 1. 84 1. 88 0. 95 5. 35 4. 26 3. 81 3. 18 4. 69 3. 44 4. 86 3. 69 5. 81 5. 55 4. 95 4. 47 4

Step 2: Plan • Since data come in matched pairs, we calculate the difference within pairs • Call this new variable “delta” (Δ) • Analyze Δ with t procedures Day 1 2 3 4 5 6 7 8 Inference about µ region Difference A–B A B 2. 92 1. 84 1. 08 1. 88 0. 95 0. 93 5. 35 4. 26 1. 09 3. 81 3. 18 0. 63 4. 69 3. 44 1. 25 4. 86 3. 69 1. 17 5. 81 4. 95 0. 86 5. 55 4. 47 1. 08 5

11/26 Quiz: Concepts Inference = generalizing from sample to population with calculated degree of certainty Complete these sentence: 1. The two forms of statistical inference are ANS: confidence intervals [estimation] and significance [hypothesis] testing 2. The population for the illustrative example (“Pollution”) in this lecture is… ANS: pollution levels in region A minus B at all times • The parameter we wish to infer in the “Pollution” illustrative example is (use symbols and words) … ANS: mean difference μ for the population described in #2 • Based on what I’ve learned in Chapter 14, 15, and 17, the estimate for the parameter in question #3 is ANS: sample mean difference x-bar 6

Step 2: Plan (cont. ) • Identify parameter • Let µ represent mean dif in pollution all days Day 1 2 3 4 5 6 7 8 • State Null hypothesize • H 0: μ = 0 • State alternative hypothesis • H a: μ ≠ 0 • Use t procedures directed against the delta variable Inference about µ region A B 2. 92 1. 84 1. 88 0. 95 5. 35 4. 26 3. 81 3. 18 4. 69 3. 44 4. 86 3. 69 5. 81 4. 95 5. 55 4. 47 Difference Δ 1. 08 0. 93 1. 09 0. 63 1. 25 1. 17 0. 86 1. 08 7

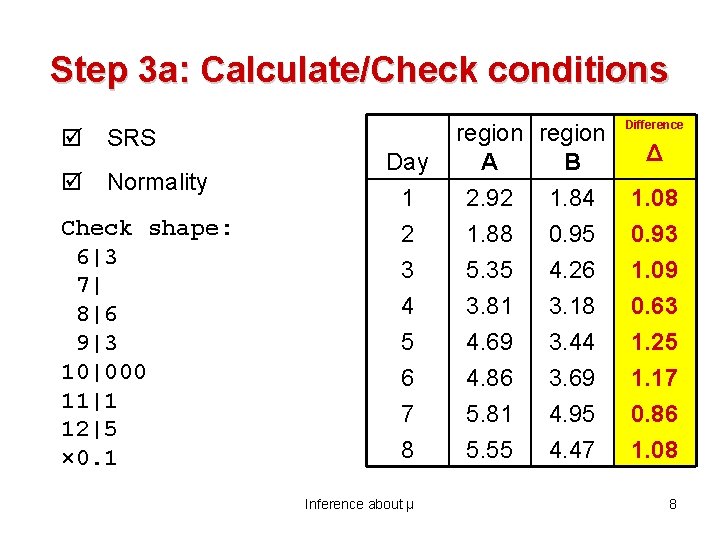
Step 3 a: Calculate/Check conditions SRS Normality Check shape: 6|3 7| 8|6 9|3 10|000 11|1 12|5 × 0. 1 Day 1 2 3 4 5 6 7 8 Inference about µ region A B 2. 92 1. 84 1. 88 0. 95 5. 35 4. 26 3. 81 3. 18 4. 69 3. 44 4. 86 3. 69 5. 81 4. 95 5. 55 4. 47 Difference Δ 1. 08 0. 93 1. 09 0. 63 1. 25 1. 17 0. 86 1. 08 8

Step 3 b&c: Test statistic & P value • • One-tailed P <. 0005 Two-tailed P-value <. 001 Inference about µ 9

Step 4: Conclusion • • When the P is low H 0 must go Region A has significantly higher pollution levels the Region B (P <. 001) Inference about µ 10

In class 11

Stop here 12