Chapter 17 Factorial Analysis of Variance Observational Data
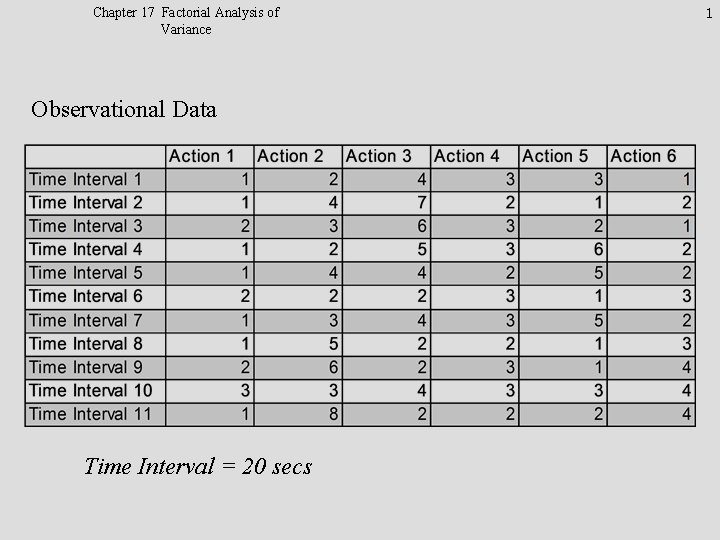
Chapter 17 Factorial Analysis of Variance Observational Data Time Interval = 20 secs 1
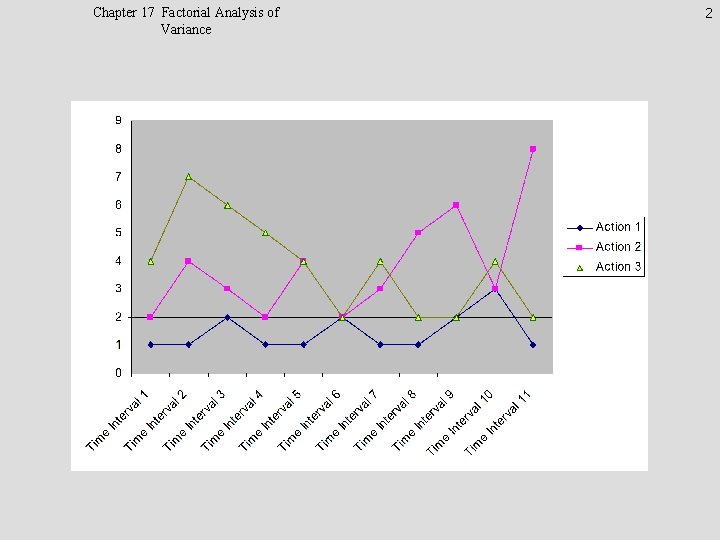
Chapter 17 Factorial Analysis of Variance 2

Chapter 17 Factorial Analysis of Variance 3 Factorial Analysis of Variance • What is a factorial design? • Main effects • Interactions • Simple effects • Magnitude of effect Cont.

Chapter 17 Factorial Analysis of Variance What is a Factorial • At least two independent variables • All combinations of each variable • R X C factorial • Cells 4

Chapter 17 Factorial Analysis of Variance 2 X 2 Factorial 5

Chapter 17 Factorial Analysis of Variance Main effects If you have two factors in the experiment: Age and Instruction Condition. If you look at the effect of age, ignoring Instruction for the time being, you are looking at the main effect of age. If we look at the effect of instruction, ignoring age, then you are looking at the main effect of instruction. 6

Chapter 17 Factorial Analysis of Variance Simple effects If you look at the effect of age at one level of instruction, then that is a simple effect. If you could restrict yourself to one level of one IV for the time being, and looking at the effect of the other IV within that level. 7
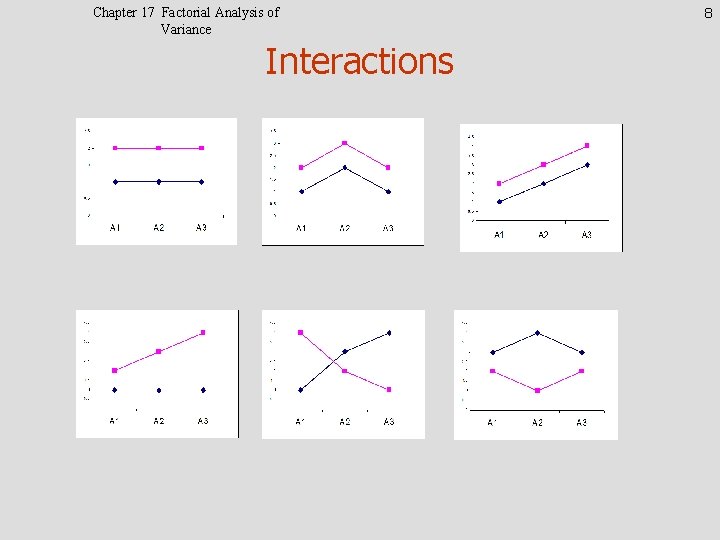
Chapter 17 Factorial Analysis of Variance Interactions 8

Chapter 17 Factorial Analysis of Variance Magnitude of Effect F ratio is biased because it goes up with sample size. For a true estimate for the treatment effect size, use eta squared (the proportion of the treatment effect / total variance in the experiment). Eta Squared is a better estimate than F but it is still a biased estimate. A better index is Omega Squared. 9

10 Chapter 17 Factorial Analysis of Variance Magnitude of Effect • Eta Squared X Interpretation • Omega squared X Less biased estimate k = number of levels for the effect in question

Chapter 17 Factorial Analysis of Variance Omega Squared 11

Chapter 17 Factorial Analysis of Variance R 2 is also often used. It is based on the sum of squares. For experiments use Omega Squared. For correlations use R squared. Value of R square is greater than omega squared. Cohen classified effects as Small Effect: . 01 Medium Effect: . 06 Large Effect: . 15 12
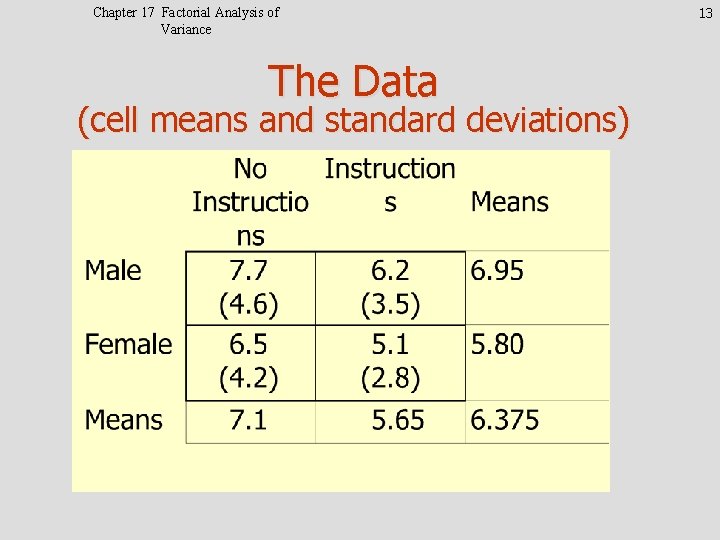
Chapter 17 Factorial Analysis of Variance The Data (cell means and standard deviations) 13
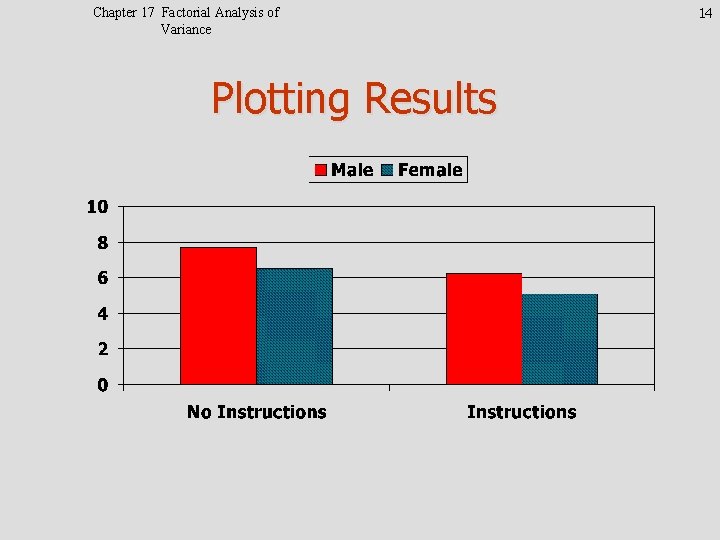
Chapter 17 Factorial Analysis of Variance Plotting Results 14

Chapter 17 Factorial Analysis of Variance 15 Effects to be estimated • Differences due to instructions X Errors more in condition without instructions • Differences due to gender X Males appear higher than females • Interaction of video and gender X What is an interaction? X Do instructions effect males and females equally? Cont.

Chapter 17 Factorial Analysis of Variance Estimated Effects--cont. • Error X average within-cell variance • Sum of squares and mean squares X Extension of the same concepts in the one-way 16

Chapter 17 Factorial Analysis of Variance 17 Calculations • Total sum of squares • Main effect sum of squares Cont.

Chapter 17 Factorial Analysis of Variance Calculations--cont. • Interaction sum of squares X Calculate SScells and subtract SSV and SSG • SSerror = SStotal - SScells X or, MSerror can be found as average of cell variances 18

Chapter 17 Factorial Analysis of Variance Degrees of Freedom • df for main effects = number of levels - 1 • df for interaction = product of dfmain effects • df error = N - ab = N - # cells • dftotal = N - 1 19

Chapter 17 Factorial Analysis of Variance 20 Calculations for Data • SStotal requires raw data. X It is actually = 171. 50 • SSvideo Cont.

Chapter 17 Factorial Analysis of Variance 21 Calculations--cont. • SSgender Cont.

Chapter 17 Factorial Analysis of Variance 22 Calculations--cont. • SScells • SSVXG = SScells - SSinstruction- SSgender = 171. 375 - 105. 125 - 66. 125 = 0. 125 Cont.

Chapter 17 Factorial Analysis of Variance Calculations--cont. • MSerror = average of cell variances = (4. 62 + 3. 52 + 4. 22 + 2. 82)/4 =58. 89/4 = 14. 723 • Note that this is MSerror and not SSerror 23
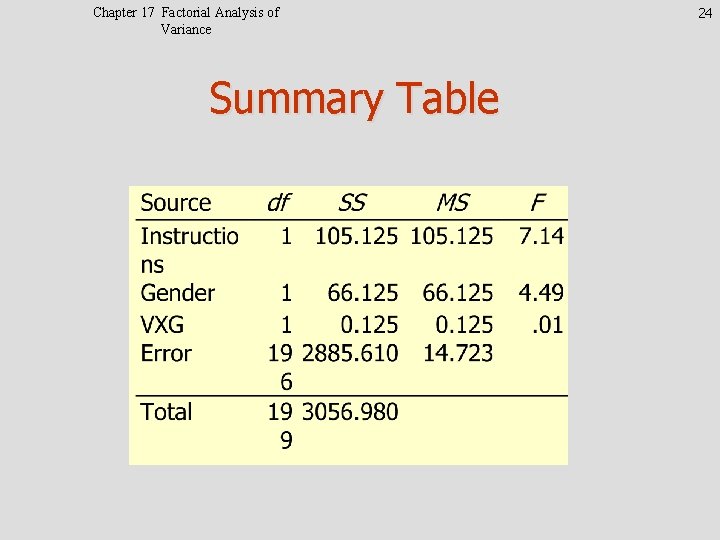
Chapter 17 Factorial Analysis of Variance Summary Table 24

Chapter 17 Factorial Analysis of Variance Elaborate on Interactions • Diagrammed on next slide as line graph • Note parallelism of lines X Instruction differences did not depend on gender 25
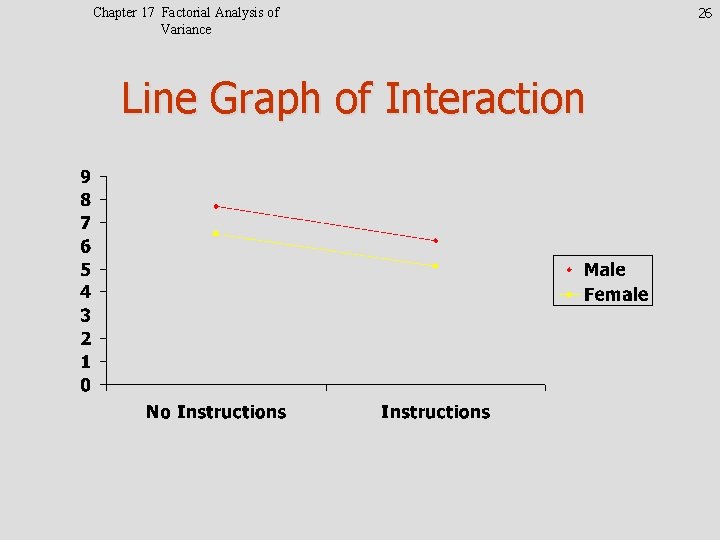
Chapter 17 Factorial Analysis of Variance Line Graph of Interaction 26
- Slides: 26