Chapter 17 Diffraction from small volumes SUMMA RY

Chapter 17 – Diffraction from small volumes SUMMA RY ANTTI MYLLYNEN

Shape effect §A reciprocal lattice of a thin sample can be associated with a rod ◦ A small space in real space gives a large lenght in reciprocal space ◦ Valid consept in every direction §The specimen can be modeled as a thin rectangular slab as shown in Figure 17. 1. §Total diffracted amplitude is the sum of is the sum of the amplitudes of each cell § Can be calculated in two ways: § The summation approach § The integration approach

The summation approach

The integration approach

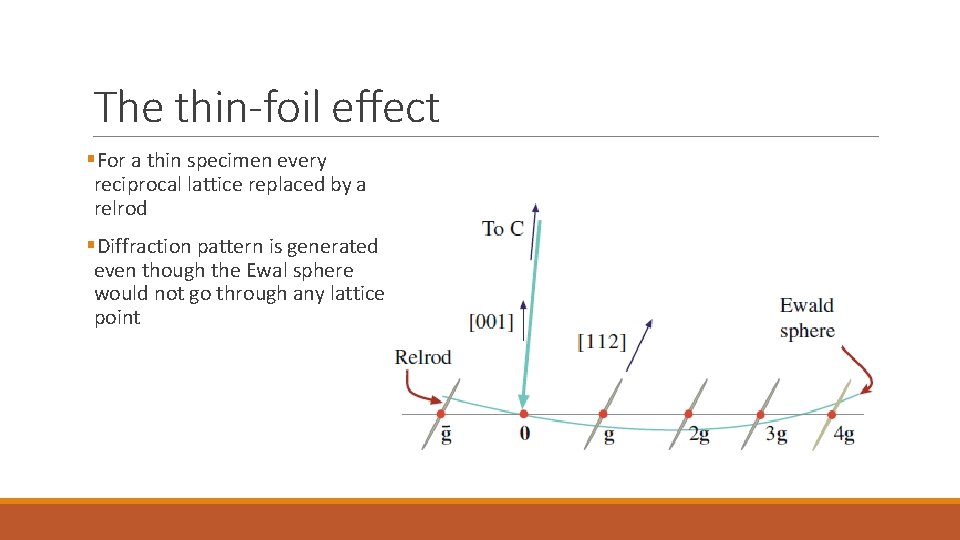
The thin-foil effect

The thin-foil effect §For a thin specimen every reciprocal lattice replaced by a relrod §Diffraction pattern is generated even though the Ewal sphere would not go through any lattice point

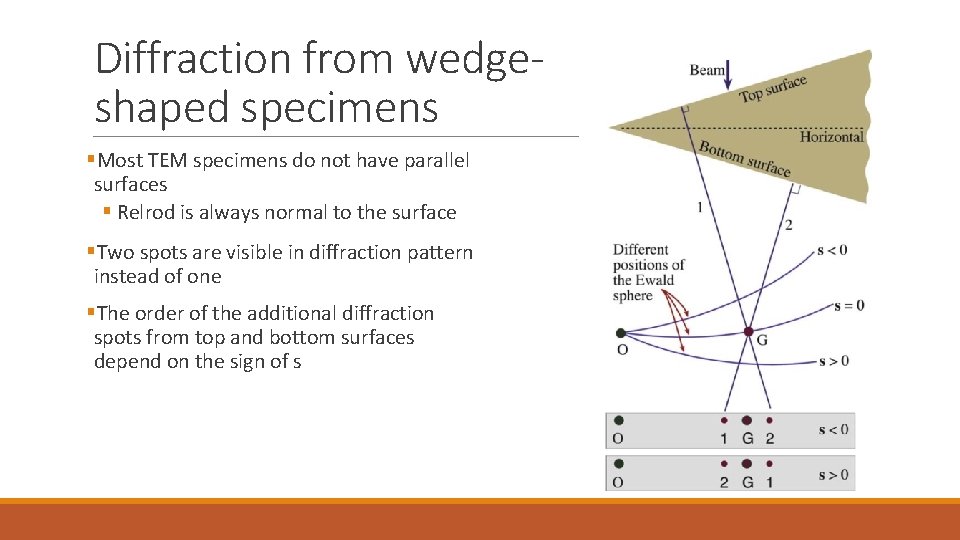
Diffraction from wedgeshaped specimens §Most TEM specimens do not have parallel surfaces § Relrod is always normal to the surface §Two spots are visible in diffraction pattern instead of one §The order of the additional diffraction spots from top and bottom surfaces depend on the sign of s

Diffraction from planar defects §A planar defect acts as an additional surface which has its own relrod § This relrod is much longer, because thickness of a defect is much smaller than the thickness of the whole specimen §In the image, 2 spots would be visible in diffraction pattern Planar defects

Diffraction from planar defects §Two possible ways to understand diffraction from planar defects 1. The defect is modeled by the thin platelet § Grains on either side of the defect contain a common reflection 2. The diffraction from the defect behaves like a wedge specimen with one surface parallel to the planar defect § Reflection is not common to the two sides

Diffraction from particles §Shape factors for different particles are shown in the image §The smallest “particle” in a specimen is often § A vacancy § A substitutional atom § An interstitial atom §A single point defect is not necessary visible in DP but diffraction effects are visible especially when diffractions from several point defects interact

Diffraction from dislocations §A dislocation is a line defect § Characterized by its line direction and its Burgers vector § The crystal structure around the dislocation is distorted or strained §A single dislocation § Causes diffuse scattering, because it’s a line defect § The strain is not high enough to cause additional spots in the DP §The diffuse intensity is not located at a reciprocal-lattice point

Diffraction from dislocations §Dislocations are present in region A but not in B §Insets show a small part of diffraction pattern §The additional points in region A are caused by the array of dislocations which is also visible in the image

Chapter summary §Samples in TEM are very small §Shape effect has to be taken into account § Particularly important for nanoparticles and nanograins § Remember that also defects in the sample has an effect on diffraction pattern