Chapter 16 PLANE MOTION OF RIGID BODIES FORCES
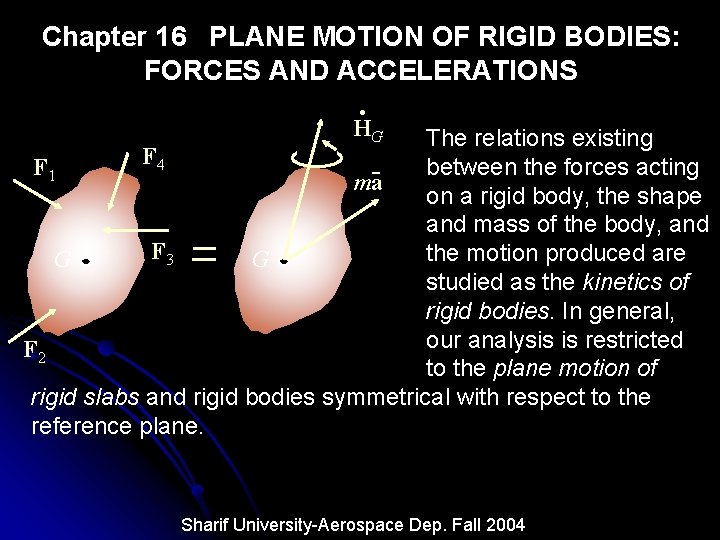
Chapter 16 PLANE MOTION OF RIGID BODIES: FORCES AND ACCELERATIONS . HG The relations existing F 4 F 1 between the forces acting ma on a rigid body, the shape and mass of the body, and F 3 the motion produced are G G studied as the kinetics of rigid bodies. In general, our analysis is restricted F 2 to the plane motion of rigid slabs and rigid bodies symmetrical with respect to the reference plane. Sharif University-Aerospace Dep. Fall 2004

. F 1 G HG F 4 F 3 ma G F 2 The two equations for the motion of a system of particles apply to the most general case of the motion of a rigid body. The first equation defines the motion of the mass center G of the body. SF = ma where m is the mass of the body, and a the acceleration of G. The second is related to the motion of the body relative to a centroidal frame of reference. . SMG = HG

. F 1 G F 2 HG F 4 F 3 ma SF = ma. . SMG = HG. G where HG is the rate of change of the angular momentum HG of the body about its mass center G. These equations express that the system of the external forces is equipollent to the system consisting of the vector ma attached. at G and the couple of moment HG.

. F 1 G HG F 4 ma F 3 G F 2 For the plane motion of rigid slabs and rigid bodies symmetrical with respect to the reference plane, the angular momentum of the body is expressed as HG = Iw where I is the moment of inertia of the body about a centroidal axis perpendicular to the reference plane and w is the angular velocity of the body. Differentiating both members of this equation . . HG = Iw = Ia
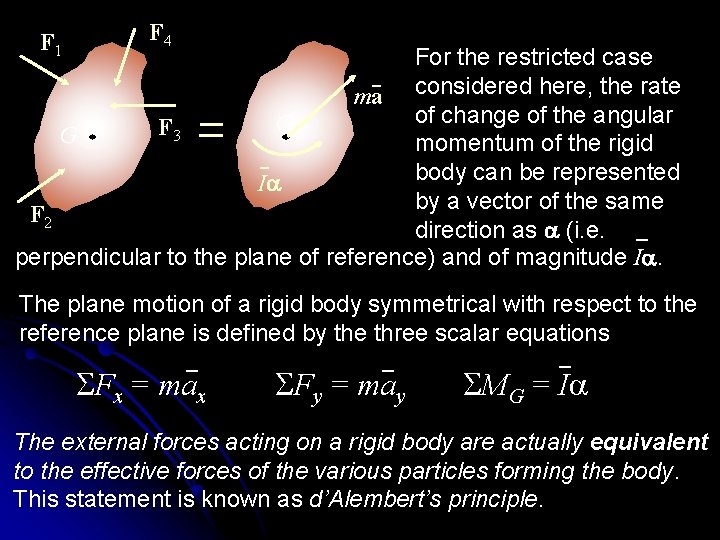
F 1 F 4 For the restricted case ma considered here, the rate of change of the angular G F 3 G momentum of the rigid body can be represented Ia by a vector of the same F 2 direction as a (i. e. perpendicular to the plane of reference) and of magnitude Ia. The plane motion of a rigid body symmetrical with respect to the reference plane is defined by the three scalar equations SFx = max SFy = may SMG = Ia The external forces acting on a rigid body are actually equivalent to the effective forces of the various particles forming the body. This statement is known as d’Alembert’s principle.
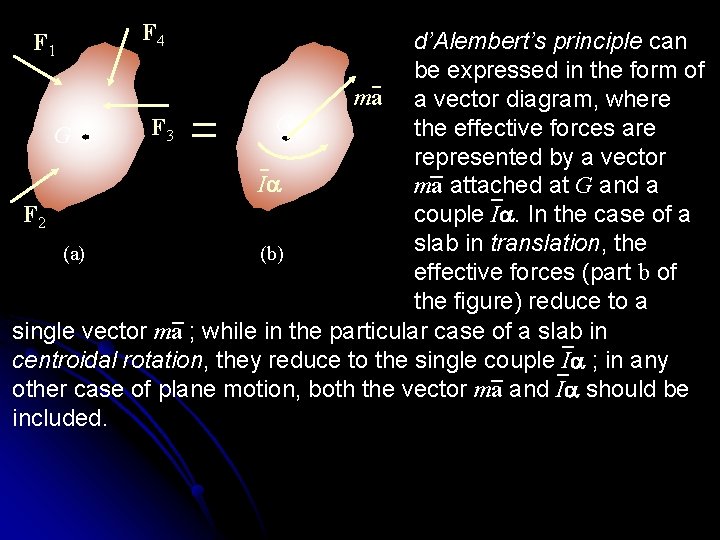
F 4 d’Alembert’s principle can be expressed in the form of ma a vector diagram, where G F 3 the effective forces are G represented by a vector Ia ma attached at G and a F 2 couple Ia. In the case of a slab in translation, the (a) (b) effective forces (part b of the figure) reduce to a single vector ma ; while in the particular case of a slab in centroidal rotation, they reduce to the single couple Ia ; in any other case of plane motion, both the vector ma and Ia should be included. F 1

F 4 Any problem involving the plane motion of a rigid slab ma may be solved by drawing a free-body-diagram equation G F 3 G similar to that shown. Three equations of of motion can Ia then be obtained by F 2 equating the x components, y components, and moments about an arbitrary point A, of the forces and vectors involved. F 1 This method can be used to solve problems involving the plane motion of several connected rigid bodies. Some problems, such as noncentroidal rotation of rods and plates, the rolling motion of spheres and wheels, and the plane motion of various types of linkages, which move under constraints, must be supplemented by kinematic analysis.
- Slides: 7