Chapter 16 Oneway Analysis of Concept Map Variance

Chapter 16 One-way Analysis of Concept Map. Variance For Statistics as taught in IS 271 Analysis of (a work in progress) Relationships Interval Data Analysis of Differences Dependent Groups Independent Groups Between Multiple Groups Nominal / Ordinal Data Multiple Predictors Independent Groups Between Two Groups Type of Data One Predictor Dependent Groups Regression Multiple Regression Independent Samples t-test Repeated Measures t-test Independent Samples ANOVA Repeated Measures ANOVA Correlation: Spearman Ordinal Frequency Rashmi Sinha Correlation: Pearson Regression CHI Square Some kinds of Regression 1

Analysis of Variance or F test ANOVA is a technique for using differences between sample means to draw inferences about the presence or absence of differences between populations means. • The logic • Calculations in SPSS • Magnitude of effect: eta squared, omega squared Chapter 16 One-way Analysis of Variance

Chapter 16 One-way Analysis of Variance Assumptions of ANOVA • Assume: X Observations normally distributed within each population X Population variances are equal • Homogeneity of variance or homoscedasticity X Observations are independent 3

Chapter 16 One-way Analysis of Variance Assumptions--cont. • Analysis of variance is generally robust to first two X A robust test is one that is not greatly affected by violations of assumptions. 4

Chapter 16 One-way Analysis of Variance Logic of Analysis of Variance • Null hypothesis (Ho): Population means from different conditions are equal X m 1 = m 2 = m 3 = m 4 • Alternative hypothesis: H 1 X Not all population means equal. 5

6 Chapter 16 One-way Analysis of Variance Lets visualize total amount of variance in an experiment Total Variance = Mean Square Total Between Group Differences (Mean Square Group) Error Variance (Individual Differences + Random Variance) Mean Square Error F ratio is a proportion of the MS group/MS Error. The larger the group differences, the bigger the F The larger the error variance, the smaller the F

Chapter 16 One-way Analysis of Variance Logic--cont. • Create a measure of variability among group means X MSgroup • Create a measure of variability within groups X MSerror 7

Chapter 16 One-way Analysis of Variance Logic--cont. • Form ratio of MSgroup /MSerror X Ratio approximately 1 if null true X Ratio significantly larger than 1 if null false X “approximately 1” can actually be as high as 2 or 3, but not much higher 8

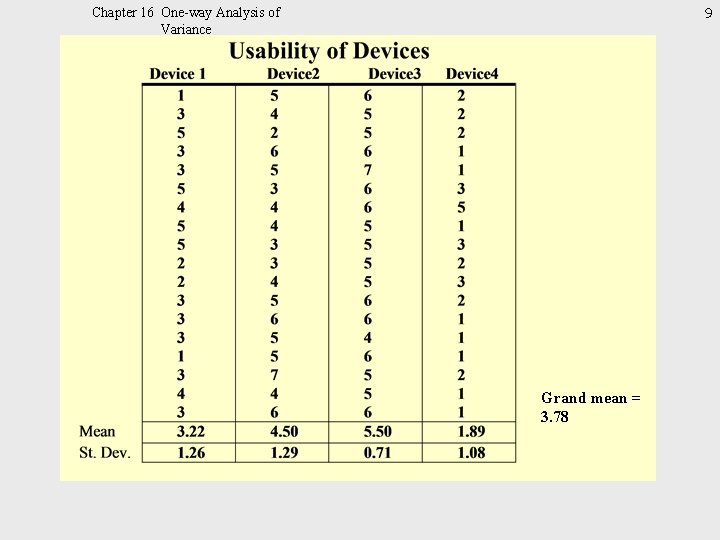
9 Chapter 16 One-way Analysis of Variance Grand mean = 3. 78

Chapter 16 One-way Analysis of Variance 10 Calculations • Start with Sum of Squares (SS) X We need: • SStotal • SSgroups • SSerror • Compute degrees of freedom (df ) • Compute mean squares and F Cont.

Chapter 16 One-way Analysis of Variance Calculations--cont. 11

Chapter 16 One-way Analysis of Variance Degrees of Freedom (df ) • Number of “observations” free to vary X dftotal = N - 1 • N observations X dfgroups = g - 1 • g means X dferror = g (n - 1) • n observations in each group = n - 1 df • times g groups 12

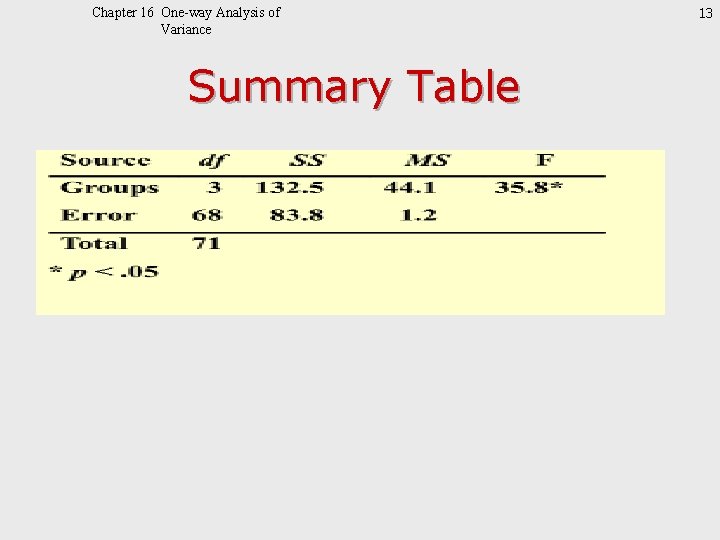
Chapter 16 One-way Analysis of Variance Summary Table 13

Chapter 16 One-way Analysis of Variance When there are more than two groups • Significant F only shows that not all groups are equal X We want to know what groups are different. • Such procedures are designed to control familywise error rate. X Familywise error rate defined X Contrast with per comparison error rate 14

Chapter 16 One-way Analysis of Variance Multiple Comparisons • The more tests we run the more likely we are to make Type I error. X Good reason to hold down number of tests 15

Chapter 16 One-way Analysis of Variance 16 Bonferroni t Test • Run t tests between pairs of groups, as usual X Hold down number of t tests X Reject if t exceeds critical value in Bonferroni table • Works by using a more strict level of significance for each comparison Cont.

Chapter 16 One-way Analysis of Variance Bonferroni t--cont. • Critical value of a for each test set at. 05/c, where c = number of tests run X Assuming familywise a =. 05 X e. g. with 3 tests, each t must be significant at. 05/3 =. 0167 level. • With computer printout, just make sure calculated probability <. 05/c • Necessary table is in the book 17

Chapter 16 One-way Analysis of Variance 18 Magnitude of Effect • Why you need to compute magnitude of effect indices • Eta squared (h 2) X Easy to calculate X Somewhat biased on the high side X Formula • See slide #33 X Percent of variation in the data that can be attributed to treatment differences Cont.

Chapter 16 One-way Analysis of Variance Magnitude of Effect--cont. • Omega squared (w 2) X Much less biased than h 2 X Not as intuitive X We adjust both numerator and denominator with MSerror X Formula on next slide 19

Chapter 16 One-way Analysis of Variance h 2 and w 2 for Foa, et al. • h 2 =. 18: 18% of variability in symptoms can be accounted for by treatment • w 2 =. 12: This is a less biased estimate, and note that it is 33% smaller. 20