Chapter 16 Data Analysis Examination of Differences 2005

Chapter 16 Data Analysis: Examination of Differences © 2005 Thomson/South-Western 1

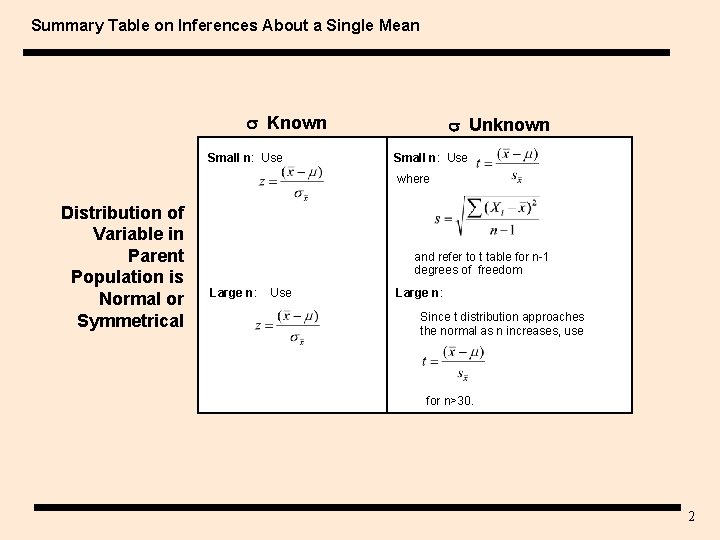
Summary Table on Inferences About a Single Mean Known Small n: Use Unknown Small n: Use where Distribution of Variable in Parent Population is Normal or Symmetrical and refer to t table for n-1 degrees of freedom Large n: Use Large n: Since t distribution approaches the normal as n increases, use for n>30. 2

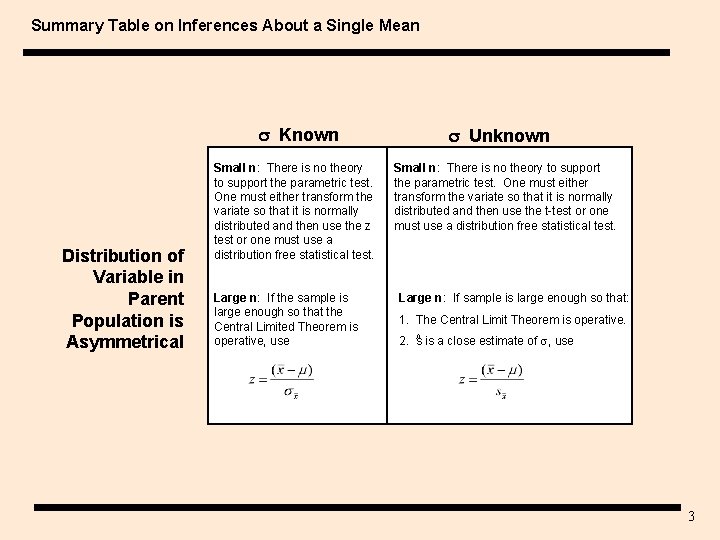
Summary Table on Inferences About a Single Mean Known Distribution of Variable in Parent Population is Asymmetrical Small n: There is no theory to support the parametric test. One must either transform the variate so that it is normally distributed and then use the z test or one must use a distribution free statistical test. Large n: If the sample is large enough so that the Central Limited Theorem is operative, use Unknown Small n: There is no theory to support the parametric test. One must either transform the variate so that it is normally distributed and then use the t-test or one must use a distribution free statistical test. Large n: If sample is large enough so that: 1. The Central Limit Theorem is operative. 2. ^s is a close estimate of , use 3

Summary Table on Inferences About the Difference in Two Means Known Small n: Unknown Small n: Can you assume 1 = 2? 1. Yes: Use pooled variance t-test where Use and Distribution of Variable in Parent Population is Normal or Symmetrical where with n 1+n 2 -2 degrees of freedom. 2. No: Approach is shrouded in controversy. Might use Aspin-Welch test. Large n: Use and use pooled variance if variances can be assumed equal, unpooled variance if equality assumption is not warranted. 4

Summary Table on Inferences About the Difference in Two Means Known Distribution of Variables in Parent Population are Asymmetrical Unknown Small n: There is no theory to support the parametric test. One must either transform the variates so that they are normally distributed and then use the z -test or one must use a distribution free statistical test. Small n: There is no theory to support the parametric test. One must either transform the variates so that they are normally distributed and then use the ttest or one must use a distribution free statistical test. Large n: If the individual samples are large enough so that the Central Limit Theorem is operative for them separately, it will also apply for their sum or difference. Use Large n: One must assume that n 1 and n 2 are large enough so that the Central Limit Theorem applies to the individual sample means. Then it can also be assumed to apply to their sum or difference. Use employing a pooled variance if the unknown parent population variances can be assumed equal and unpooled variance if the equality assumption is not warranted. 5

Appendix 16 Analysis of Variance 6

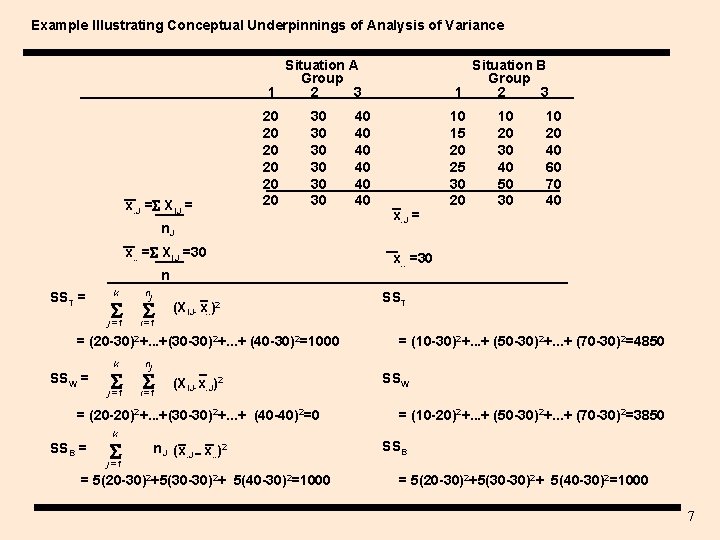
Example Illustrating Conceptual Underpinnings of Analysis of Variance Situation A Group 1 2 3 x. J = XIJ = 20 20 20 30 30 30 n. J x. . = XIJ =30 n SST = k nj i=1 j=1 (XIJ- x. . )2 = (20 -30)2+. . . +(30 -30)2+. . . + (40 -30)2=1000 k SSW = nj i=1 j=1 (XIJ-x. J)2 = (20 -20)2+. . . +(30 -30)2+. . . + (40 -40)2=0 k SSB = j=1 n. J (x. J x. . )2 = 5(20 -30)2+5(30 -30)2+ 5(40 -30)2=1000 40 40 40 Situation B Group 1 2 3 x. J = 10 15 20 25 30 20 10 20 30 40 50 30 10 20 40 60 70 40 x. . =30 SST = (10 -30)2+. . . + (50 -30)2+. . . + (70 -30)2=4850 SSW = (10 -20)2+. . . + (50 -30)2+. . . + (70 -30)2=3850 SSB = 5(20 -30)2+5(30 -30)2+ 5(40 -30)2=1000 7

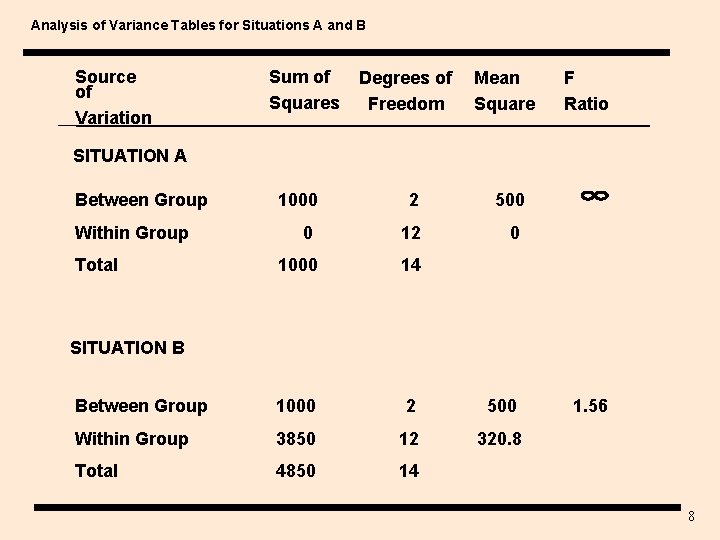
Analysis of Variance Tables for Situations A and B Source of Variation Sum of Squares Degrees of Freedom Mean Square F Ratio SITUATION A Between Group 1000 2 500 0 12 0 1000 14 Between Group 1000 2 500 Within Group 3850 12 320. 8 Total 4850 14 Within Group Total SITUATION B 1. 56 8