Chapter 15 Relational Design Algorithms and Further Dependencies

Chapter 15 Relational Design Algorithms and Further Dependencies • Relational Databases Design Algorithms – Relational Decomposition – The Dependency Preservation Property – The Loossless Join Property – Null Values and Dangling Tuples • Further Dependencies and Normal Forms – Multivalued Dependencies and 4 NF – Join Dependencies and 5 NF – Inclusion Dependencies

(cont. ) – Template Dependencies – Domain-Key Normal Form

1 Relational Databases Design Algorithms • Normal forms are not sufficient criteria for a good design • Example: Any relation with two attributes is always in BCNF-so we can create 2 -attribute relations arbitrarily and get BCNF • Additional conditions are needed to ensure a good design – Lossless join property – Dependency preserving property

1. 1 Relational Decomposition • We start with a universal relation schema R containing all the database attributes: R= {A 1, A 2, …, An} • The design goal is a decomposition D of R into m relation schemas: D = {R 1, R 2, …, Rm} • Each relation schema Ri contains a subset of the attributes of R • Every attribute in R should appear in at least one Ri

1. 2 The Dependency Preservation Property • The database designers define a set F of functional dependencies that should hold on the attributes of R • D should preserve the dependencies; informally, the collection of all dependencies that hold on the individual relations Ri should be equivalent to F • Formally: – Define the projection of F on Ri, denoted by F(Ri), to be the set of FDs X Y in F+ such that (X Y) Ri

(cont. ) – A decomposition D = {R 1, R 2, …, Rm} is dependency preserving if ( F(R 1) F(R 2) … F(Rm))+ = F+ – This property makes it possible to ensure that the FDs in F hold simply by ensuring that the dependencies on each relation Ri hold individually – There is an algorithm to decompose R into a dependency preserving decomposition D = {R 1, R 2, …, Rm} with respect to F such that each Ri is in 3 NF

(cont. ) – Called the relational synthesis algorithm • Find a minimal set of FDs G equivalent to F • For each X of an FD X A in G Create a relation schema Ri in D with the attributes {X A 1 A 2 … Ak} where the Aj’s are all the attributes appearing in an FD in G with X as left hand side • If any attributes in R are not placed in any Ri, create another relation in D for these attributes – It can be proven that all dependencies in F are preserved and that all relation schemas in D are in 3 NF

(cont. ) • Problems: – Must find a minimal cover G for F – No efficient algorithm for finding a minimal cover – Several minimal covers can exist for F; the result of the algorithm can be different depending on which is chosen

1. 3 The Lossless(Non-Additive) Join Property • Informally, this property ensures that no spurious tuples appear when the relations in the decomposition are JOINed • Formally: – A decomposition D = {R 1, R 2, …, Rm} of R has the lossless join property with respect to a set F of FDs if, for every relation instance r® whose tuples satisfy all the FDs in F, we have: ( R 1(r(R)) R 2(r(R)) … Rm(r(R))) = r(R) – This condition ensures that whenever a relation instance r(R) satisfies F, no spurious tuples are generated by joining the decomposed relations r(Ri)

(cont. ) • Since we actually store the decomposed relations as base relations, this condition is necessary to generate meaningful results for queries involving JOINs • There is an algorithm for testing whether a decomposition D satisfies the lossless join property with respect to a set F of FDs

Figure 15. 1

(cont. ) • There is an algorithm for decomposing R into BCNF relations such that the decomposition has the lossless join property with respect to a set of FDs F on R – Set D {R} – While there is a relation schema Q in D that is not in BCNF do Begin Choose one Q in D that is not in BCNF; Find a FD X Y in Q that violates BCNF; Replace Q in D by two relation schemas(Q-Y) and (X Y) end;

(cont. ) • This is based on two properties of lossless join decomposition: – The decomposition D = {R 1, R 2} of R has the lossless join property w. r. t F if and only if either: • The FD (R 1 R 2) (R 1 R 2) is in F+, or • The FD (R 1 R 2) (R 2 R 1) is in F+ – If D = {R 1, R 2, …, Rm} of R has the lossless join property w. r. t a set F, and D 1 = {Q 1, Q 2, …, Qk} of Ri has the lossless join property w. r. t. F(Ri) then D = {R 1, R 2, …, Ri-1, Q 2, …, Qk. Ri+1, … Rm} has the lossless join property w. r. t F

(cont. ) – Meaning: if D is already lossless in join, then any decomposition Di of Ri that is also lossless in join will also make D lossless in join. – There is no algorithm for decomposition into BCNF relations that is dependency preserving – A modification of the synthesis algorithm guarantees both the lossless join and dependency preserving properties but into 3 NF relations (not BCNF) – Fortunately, many 3 NF relations are also in BCNF • Lossless join and dependency preserving decomposition into 3 NF relations:

(cont. ) – Find a minimal set of FDs G equivalent to F – For each X of an FD X Y in G Create a relation schema Ri in D with the attributes {X A 1 A 2 … Ak} where the Aj’s are all the attributes appearing in an FD in G with X as left hand side – If any attributes in R are not placed in any Ri, create another relation in D for these attributes – If none of the relations in D contain a key of R, create a relation that contains a key of R and add it to D

1. 4 Null Values and Dangling Tuples • Null values may create problems if they appear as join attributes • The distinction between the result of a regular join and an outer join becomes important when specifying queries • Some queries require regular join and other queries require outer join • Dangling tuples: – Sometimes the attributes of a relation are “partitioned” into several relations with the primary key repeated in each of the relations

(cont. ) – Tuples whose primary key does not appear in all of the relations are called “dangling tuples” – If a regular join is taken on the relations on the primary key to rebuild the tuples, the dangling tuples do not appear in the result

Figure 15. 2

Figure 15. 3

2. Further Dependencies and Normal Forms • Functional dependencies(FDs) are used to specify one very common type of constraint • Other types of constraints cannot be specified by FDs alone • Additional dependencies include multivalued dependencies(MVDs), join dependencies(JDs), inclusion dependencies • Some dependencies lead to normal forms beyond 3 NF and BCNF

2. 1 Multivalued Dependencies and 4 NF • Informally, a set of attributes X multidetermines a set of attributes Y if the value of X determines a set of values for Y(independently of any other attributes) • A multi-valued dependency (MVD) is written as X Y • Specifies a constraint on all relation instances r(R) • Formally: – Let R be a relation schema; let X and Y be subsets of the attributes in R; and let X = R (X Y) (the remaining attributes)

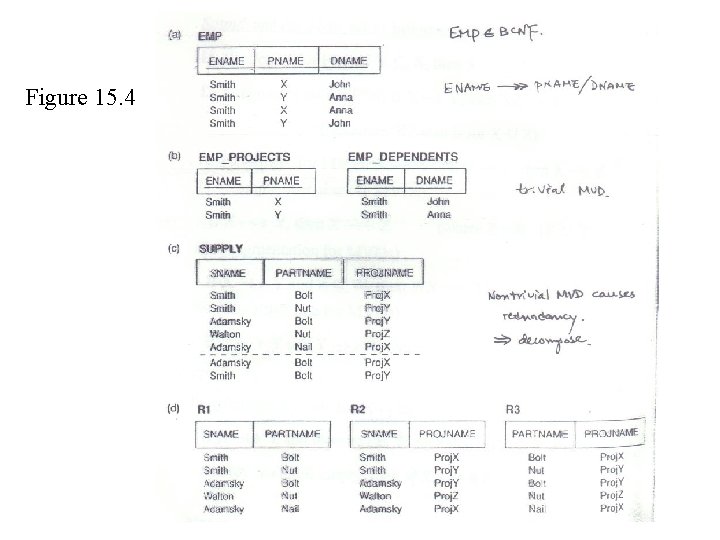
(cont. ) – An MVD X Y holds in R if whenever two tuples t 1 and t 2 exist in a relation instance r(R) with t 1[X] = t 2[X], then two tuples t 3 and t 4 must also exist in r(R) such that the follwing holds: t 1: x y 1 z 1 t 2: x y 2 z 2 – t 3[X] = t 4[X] = t 1[X] = t 2[X] t 3: x y 1 z 2 – t 3[Y] = t 1[Y] and t 4[Y] = t 2[Y] t 4: x y 2 z 1 – t 3[Z] = t 2[Z] and t 4[Z] = t 1[Z] x y – The MVD constraint implies that a value of X determines a set of values of Y independently from the values of Z – Property of MVD: If X Y holds, then X Z also holds x y/z

(cont. ) – An MVD X Y is called a trivial MVD if either: (a) Y X or, (b) (X Y) = R – A trivial MVD always holds according to the formal MVD definition

Figure 15. 4

(cont. ) – Given a set F of FDs and MVDs, we can infer additional FDs and MVDs that hold whenever the dependencies in F hold • Sound and complete set of inference rules for FDs and MVDs: – (Reflexive for FDs) If Y X, then X Y – (Augmentation for FDs) If X Y, then XZ YZ (Notation: XZ stands for X Z) – (Transitive for FDs) If X Y and Y Z, then X Z

(cont. ) – (Complementation for MVDs) If X Y, then X Z (where Z = R (X Y)) – (Augmentation for MVDs) If X Y and Z W, then WX YZ – (Transitive rule for MVDs) If X Y and Y Z, then X (Z Y) – (Relication rule FD to MVD) If X Y, then X Y – (Coalescence rule for MVDs) If X Y and there exists W such that (a) Z Y, (b) W Z, and (c) W Y is empty, then X Z

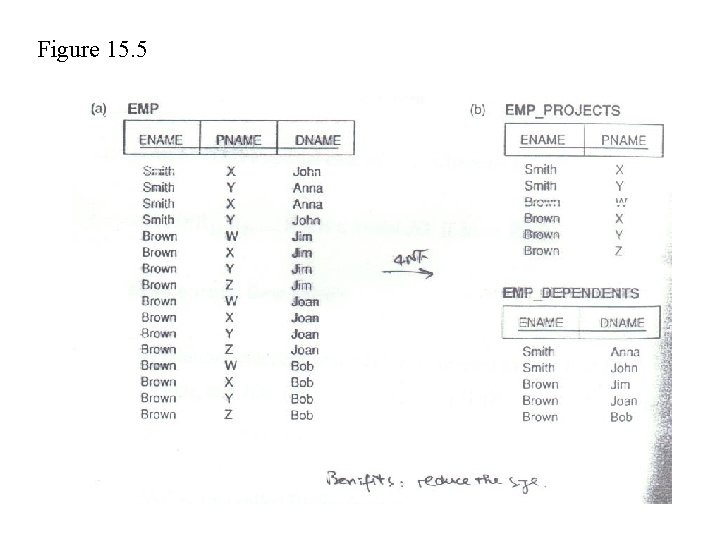
(cont. ) • Notes: – By rule I 7, every FD is also an MVD – I 1 to I 8 can derive the closure F+ of a set of dependencies F • Fourth Normal Form(4 NF): – 3 NF and BCNF do not deal with multivalued dependencies – A relation schema with some non-trivial MVDs may not be a good design (see Figures 15. 4 and 15. 5) – 4 NF takes care of these problems, and implies BCNF (every relation in 4 NF is also in BCNF)

(cont. ) • Formal definition of 4 NF: – A relation schema R is in 4 NF with respect to a set of (functional and multivalued) dependencies F if for every nontrivial multivalued dependency X Y in F+, X is a superkey of R – Check Fig 15. 4(a) is not in 4 NF; ENAME PNAME/DNAME But ENAME is not the superkey • Notes: – Since every FD is an MVD, 4 NF implies BCNF – If all dependencies in F are FDs, the definition for 4 NF becomes the definition for BCNF

(cont. ) • There is an algorithm for decomposing R into 4 NF relations such that the decomposition has the lossless join property with respect to a set F of FDs and MVDs on R • Algorithm 4. 5: – Set D {R} – While there is a relation schema Q in D that is not in 4 NF do begin Choose one Q in D that is not in 4 NF; Find a nontrivial MVD X Y in Q that violates 4 NF; Replace Q in D by two relation schemas (Q Y) and (X Y) end;

(cont. ) • Algorithm 15. 5 is based on property LJ 1: • A decomposition D = {R 1, R 2} of R has the lossless join property with respect to F if and only if either: • (a) (R 1 R 2) (R 1 R 2) holds in F+, or • (b) (R 1 R 2) (R 2 R 1) holds in F+

Figure 15. 5

2. 2 Join Dependencies and 5 NF • A join dependency JD(R 1, R 2, …, Rn) is a constraint on R • Specifies that every legal instance r(R) should have a lossless join decomposition into R 1, R 2, …, Rn • An MVD is a special case of a JD where n= 2 • A JD(R 1, R 2, …, Rn) is a trivial JD if some Ri = R • Fifth normal form (5 NF): – A relation schema R is in 5 NF with respect to a set F of FDs, MVDs, and JDs if for every nontrivial JD(R 1, R 2, …, Rn), each Ri is a superkey of R

(cont. ) – 5 NF is also called PJNF (project-join normal form) • Note: Unfortunately, theory of MVD and JD lossless join decomposition does not take NULL values into account

2. 3 Inclusion Dependencies • Used to specify referential integrity and class/subclass constraints between two relations R and S • An inclusion dependency R. X < S. Y specifies that at any point in time, if r(R) and s(S) are relation instances of R and S, then: • X(r(R)) Y(s(S)) • The attributes X of R and Y of S must be compatible

(cont. ) • Sound and complete inference rules for inclusion dependencies: – (ID 1) R. X < R. X – (ID 2) If R. X < S. Y, where X = {A 1, A 2, …, An}, Y = {B 1, B 2, …, Bn}, and Ai corresponds to Bi, then Ai < Bi for 1 i n – (ID 3) If R. X < S. Y and S. Y < T. Z, then R. X < T. Z • So far, there are no normal forms based on inclusion dependencies – Example: Department. DMGSSN < EMPLOYEE. SSN – WORKS_ON. PNUMBER < Project. PNUMBER