Chapter 15 Mechanical Waves Modifications by Mike Brotherton

Chapter 15 Mechanical Waves Modifications by Mike Brotherton Power. Point® Lectures for University Physics, Thirteenth Edition – Hugh D. Young and Roger A. Freedman Lectures by Wayne Anderson Copyright © 2012 Pearson Education Inc.

Goals for Chapter 15 • To study the properties and varieties of mechanical waves • To relate the speed, frequency, and wavelength of periodic waves • To interpret periodic waves mathematically • To calculate the speed of a wave on a string • To calculate the energy of mechanical waves • To understand the interference of mechanical waves • To analyze standing waves on a string • To investigate the sound produced by stringed instruments Copyright © 2012 Pearson Education Inc.

Introduction • Earthquake waves carry enormous power as they travel through the earth. • Other types of mechanical waves, such as sound waves or the vibration of the strings of a piano, carry far less energy. • Overlapping waves interfere, which helps us understand musical instruments. Copyright © 2012 Pearson Education Inc.

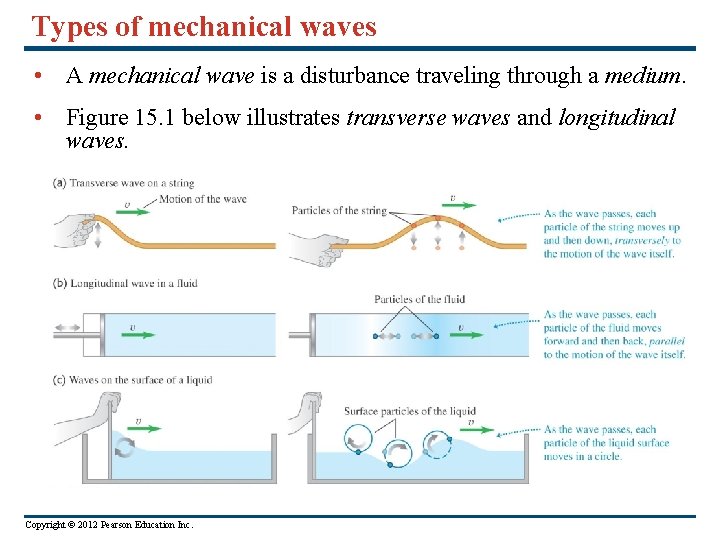
Types of mechanical waves • A mechanical wave is a disturbance traveling through a medium. • Figure 15. 1 below illustrates transverse waves and longitudinal waves. Copyright © 2012 Pearson Education Inc.

Periodic waves • For a periodic wave, each particle of the medium undergoes periodic motion. • The wavelength of a periodic wave is the length of one complete wave pattern. • The speed of any periodic wave of frequency f is v = f. Copyright © 2012 Pearson Education Inc.

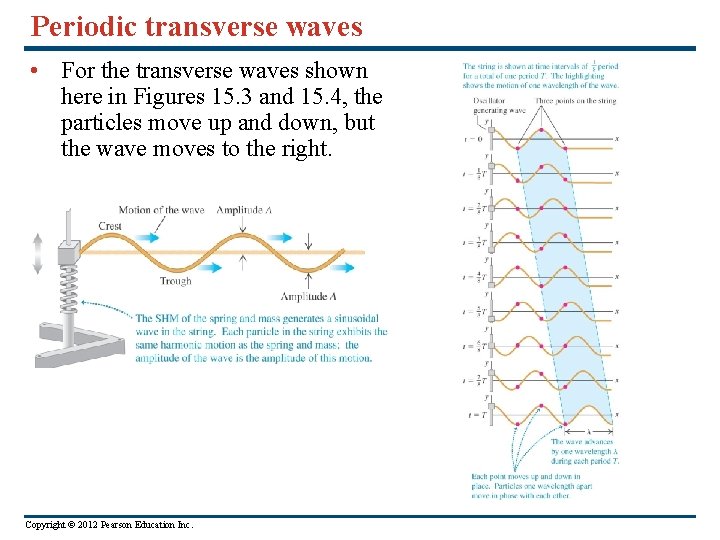
Periodic transverse waves • For the transverse waves shown here in Figures 15. 3

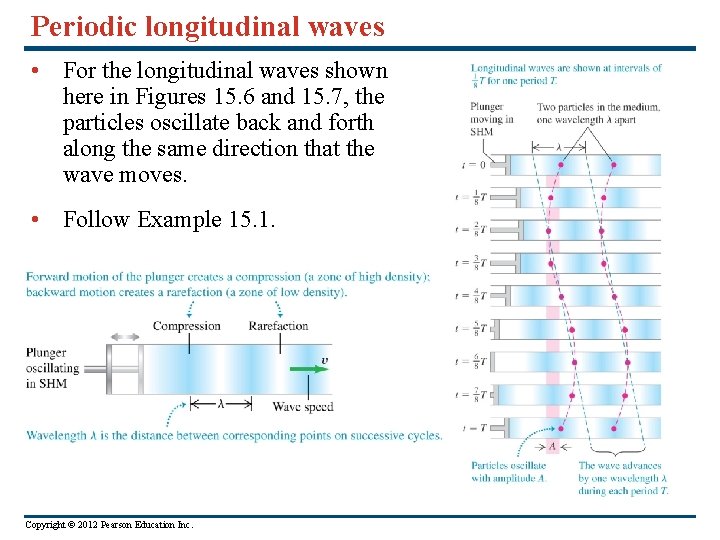
Periodic longitudinal waves • For the longitudinal waves shown here in Figures 15. 6 and 15. 7, the particles oscillate back and forth along the same direction that the wave moves. • Follow Example 15. 1. Copyright © 2012 Pearson Education Inc.

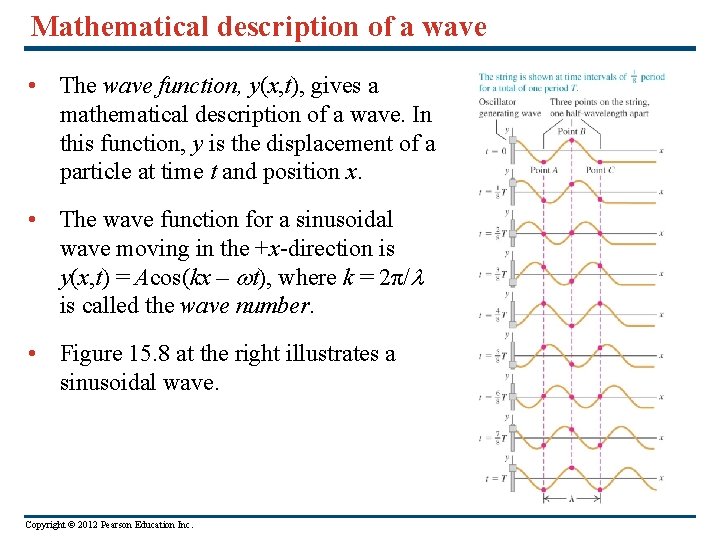
Mathematical description of a wave • The wave function, y(x, t), gives a mathematical description of a wave. In this function, y is the displacement of a particle at time t and position x. • The wave function for a sinusoidal wave moving in the +x-direction is y(x, t) = Acos(kx – t), where k = 2π/ is called the wave number. • Figure 15. 8 at the right illustrates a sinusoidal wave. Copyright © 2012 Pearson Education Inc.

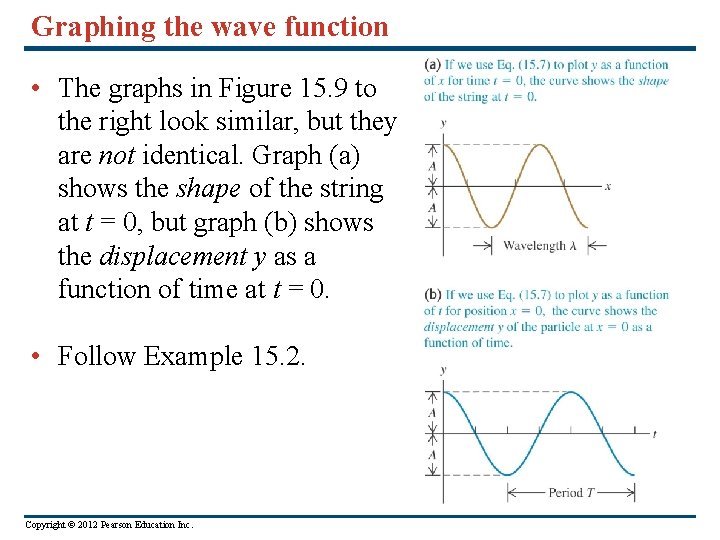
Graphing the wave function • The graphs in Figure 15. 9 to the right look similar, but they are not identical. Graph (a) shows the shape of the string at t = 0, but graph (b) shows the displacement y as a function of time at t = 0. • Follow Example 15. 2. Copyright © 2012 Pearson Education Inc.

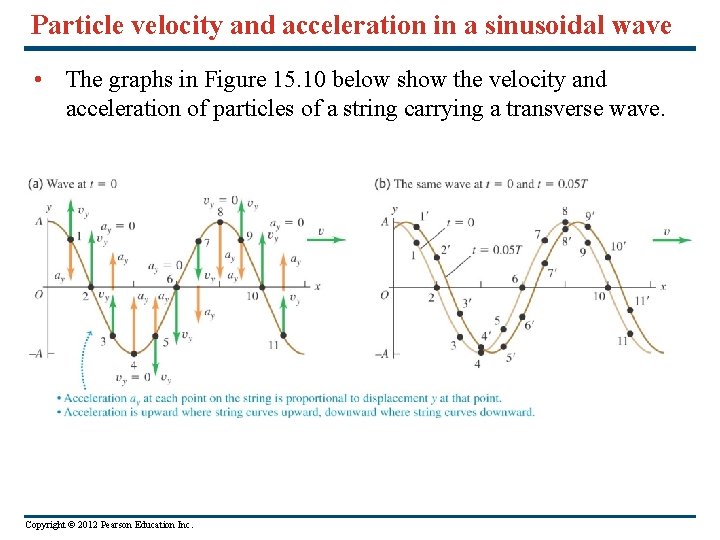
Particle velocity and acceleration in a sinusoidal wave • The graphs in Figure 15. 10 below show the velocity and acceleration of particles of a string carrying a transverse wave. Copyright © 2012 Pearson Education Inc.

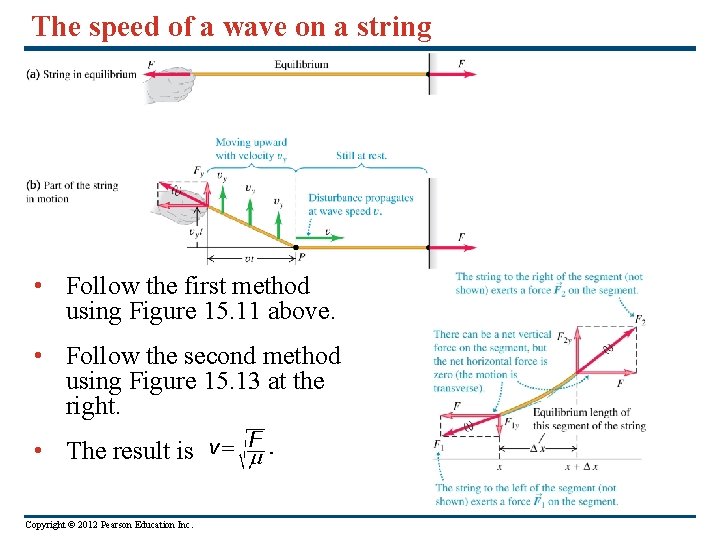
The speed of a wave on a string • Follow the first method using Figure 15. 11 above. • Follow the second method using Figure 15. 13 at the right. • The result is Copyright © 2012 Pearson Education Inc.

Calculating wave speed • Follow Example 15. 3 and refer to Figure 15. 14

Power in a wave • A wave transfers power along a string because it transfers energy. • The average power is proportional to the square of the amplitude and to the square of the frequency. This result is true for all waves. • Follow Example 15. 4. Copyright © 2012 Pearson Education Inc.

Wave intensity • The intensity of a wave is the average power it carries per unit area. • If the waves spread out uniformly in all directions and no energy is absorbed, the intensity I at any distance r from a wave source is inversely proportional to r 2: I 1/r 2. (See Figure 15. 17 at the right. ) • Follow Example 15. 5. Copyright © 2012 Pearson Education Inc.

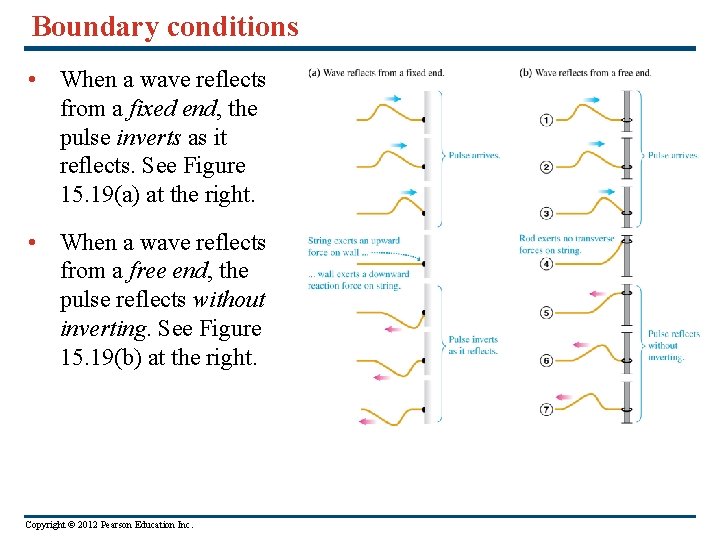
Boundary conditions • When a wave reflects from a fixed end, the pulse inverts as it reflects. See Figure 15. 19(a) at the right. • When a wave reflects from a free end, the pulse reflects without inverting. See Figure 15. 19(b) at the right. Copyright © 2012 Pearson Education Inc.

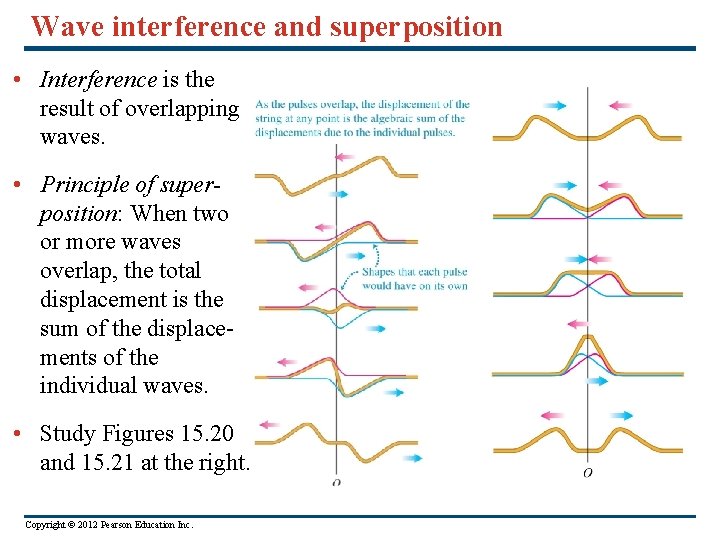
Wave interference and superposition • Interference is the result of overlapping waves. • Principle of superposition: When two or more waves overlap, the total displacement is the sum of the displacements of the individual waves. • Study Figures 15. 20 and 15. 21 at the right. Copyright © 2012 Pearson Education Inc.

Standing waves on a string • Waves traveling in opposite directions on a taut string interfere with each other. • The result is a standing wave pattern that does not move on the string. • Destructive interference occurs where the wave displacements cancel, and constructive interference occurs where the displacements add. • At the nodes no motion occurs, and at the antinodes the amplitude of the motion is greatest. • Figure 15. 23 on the next slide shows photographs of several standing wave patterns. Copyright © 2012 Pearson Education Inc.

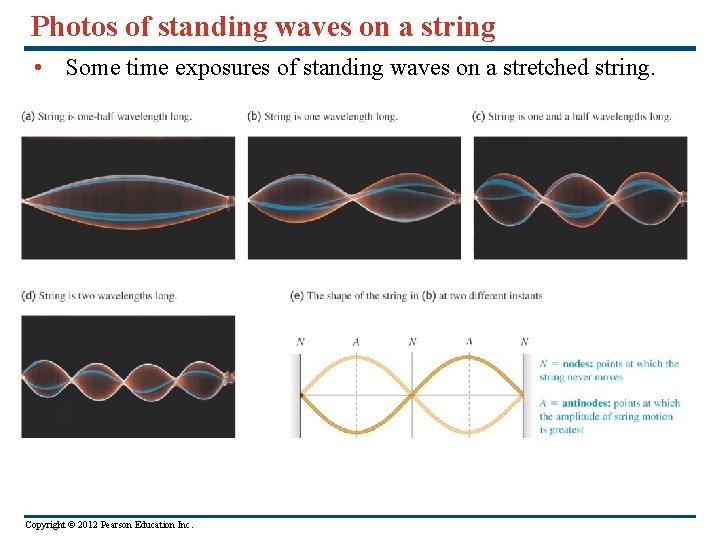
Photos of standing waves on a string • Some time exposures of standing waves

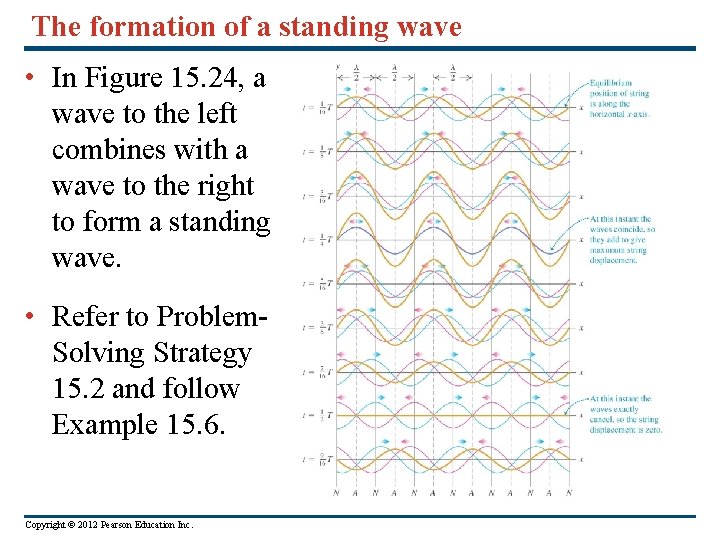
The formation of a standing wave • In Figure 15. 24, a wave to the left combines with a wave to the right to form a standing wave. • Refer to Problem. Solving Strategy 15. 2 and follow Example 15. 6. Copyright © 2012 Pearson Education Inc.

Normal modes of a string • For a taut string fixed at both ends, the possible wavelengths are n = 2 L/n and the possible frequencies are fn = n v/2 L = nf 1, where n = 1, 2, 3, … • f 1 is the fundamental frequency, f 2 is the second harmonic (first overtone), f 3 is the third harmonic (second overtone), etc. • Figure 15. 26 illustrates the first four harmonics. Copyright © 2012 Pearson Education Inc.

Standing waves and musical instruments • A stringed instrument is tuned to the correct frequency (pitch) by varying the tension. Longer strings produce bass notes and shorter strings produce treble notes. (See Figure 15. 29 below. ) • Follow Examples 15. 7 and 15. 8. Copyright © 2012 Pearson Education Inc.