Chapter 15 Market Demand Key Concept elasticity Elasticity









![• Linear demand x=a-bp, a, b>0 • | |= |(∆x/∆p)(p/x)| = |(-b)[p/(a-bp)]| • Linear demand x=a-bp, a, b>0 • | |= |(∆x/∆p)(p/x)| = |(-b)[p/(a-bp)]|](https://slidetodoc.com/presentation_image_h/8913675060677c9e1334ebbca781815c/image-11.jpg)
![• | | = |(-b)[p/(a-bp)]| • At the midpoint where p=a/2 b, • • | | = |(-b)[p/(a-bp)]| • At the midpoint where p=a/2 b, •](https://slidetodoc.com/presentation_image_h/8913675060677c9e1334ebbca781815c/image-12.jpg)

![• • MR =d. R/dx =d(px)/dx =p+(dp/dx)x =p[1+(dp/dx)(x/p)] =p(1+1/ ) =p(1 -1/| |) • • MR =d. R/dx =d(px)/dx =p+(dp/dx)x =p[1+(dp/dx)(x/p)] =p(1+1/ ) =p(1 -1/| |)](https://slidetodoc.com/presentation_image_h/8913675060677c9e1334ebbca781815c/image-15.jpg)













- Slides: 32

• Chapter 15 Market Demand • Key Concept: elasticity • Elasticity measures how responsive demand is to a change. • We make it unit free by measuring the percentage of quantity change in response to a percentage change of the variable in concern.

• Chapter 15 Market Demand • Individual i’s demand for good 1 • xi(p 1, p 2, mi) • Market demand • x(p 1, p 2, m 1, m 2, …, mn) = x 1(p 1, p 2, m 1)+ x 2(p 1, p 2, m 2)+…+xn(p 1, p 2, mn)

• x(p 1, p 2, m 1, m 2, …, mn) = x 1(p 1, p 2, m 1)+ x 2(p 1, p 2, m 2)+…+xn(p 1, p 2, mn) • Market demand depends on the distribution of income.

• Earlier we talked about inverse demand • Given a quantity, the demand gives us the marginal willingness to pay for the consumer to demand such.

• For market demand, we can interpret the inverse demand the same way. • Since at optimum, everyone chooses so that MRS equals the relative price ratio and the price ratio is common. • Hence, given a quantity demanded by all, the demand gives us the marginal willingness to pay for all.


• One way to characterize the demand is to describe how responsive it is. • For instance, how responsive demand is to price changes, income changes or price changes of other goods. • x(p 1, p 2, m)

• Price elasticity • x(p 1, p 2, m): ∆x/∆p 1 is not a good measure because it is not unit free. • We use (∆x/x)/(∆p 1/p 1) instead.

• (∆x/x)/(∆p 1/p 1) • It is negative for most demands, but sometimes we ignore the negative signs for convenience. • | |>1: elastic, | |=1: unit elastic, | |<1: inelastic

• Apple store is estimated to have the elasticity of -2. • 1% increase in price causes a 2% drop in the demand for an Apple app. • In Google Play, the elasticity is -3. 7.
![Linear demand xabp a b0 xppx bpabp • Linear demand x=a-bp, a, b>0 • | |= |(∆x/∆p)(p/x)| = |(-b)[p/(a-bp)]|](https://slidetodoc.com/presentation_image_h/8913675060677c9e1334ebbca781815c/image-11.jpg)
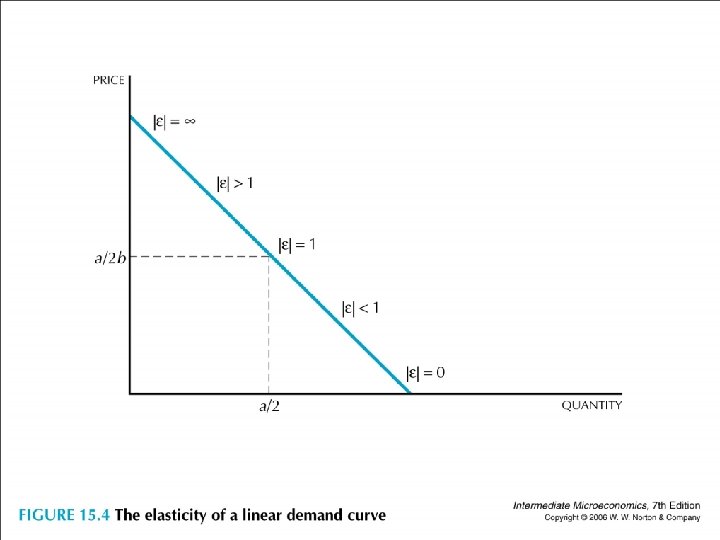
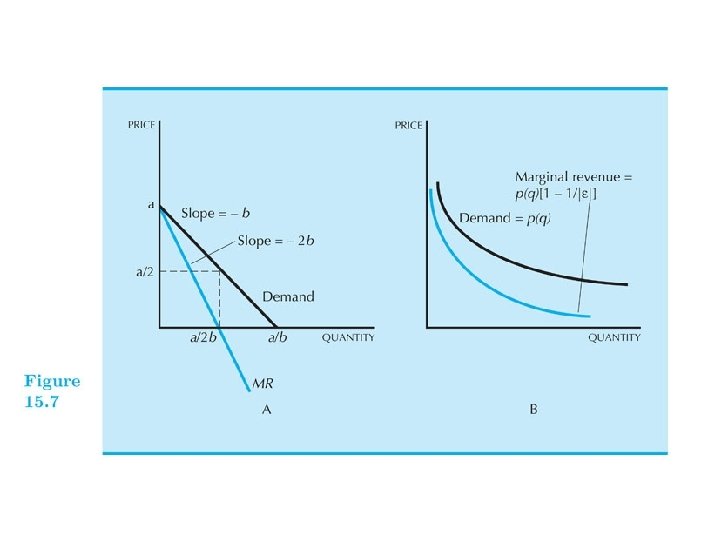
• Linear demand x=a-bp, a, b>0 • | |= |(∆x/∆p)(p/x)| = |(-b)[p/(a-bp)]|
![bpabp At the midpoint where pa2 b • | | = |(-b)[p/(a-bp)]| • At the midpoint where p=a/2 b, •](https://slidetodoc.com/presentation_image_h/8913675060677c9e1334ebbca781815c/image-12.jpg)
• | | = |(-b)[p/(a-bp)]| • At the midpoint where p=a/2 b, • | | = |(-b)[(a/2 b)/(a-b(a/2 b))]| =1. • When p is higher than the midpoint, | |>1. • When p is lower than the midpoint, | |<1.


• Can calculate the relationship between elasticity and revenue. • Revenue R=px • marginal revenue, the change of revenue when the quantity is increased • MR • =d. R/dx
![MR d Rdx dpxdx pdpdxx p1dpdxxp p11 p1 1 • • MR =d. R/dx =d(px)/dx =p+(dp/dx)x =p[1+(dp/dx)(x/p)] =p(1+1/ ) =p(1 -1/| |)](https://slidetodoc.com/presentation_image_h/8913675060677c9e1334ebbca781815c/image-15.jpg)
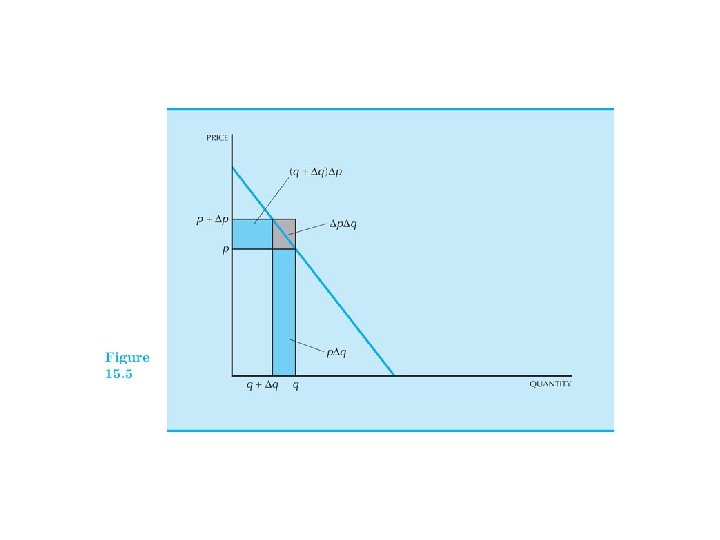
• • MR =d. R/dx =d(px)/dx =p+(dp/dx)x =p[1+(dp/dx)(x/p)] =p(1+1/ ) =p(1 -1/| |) when demand is negatively sloping.

• MR=p+(dp/dx)x, when you increase the quantity, for the marginal unit, you get an additional revenue p. • But since there is only one price, all the units sold before have to be sold at the same price. Thus the revenue is changed by the amount as well (dp/dx)x.


• Notice that MR at x=0 equals p (no units sold before) and MR at x>0 is less than p when downward sloping.

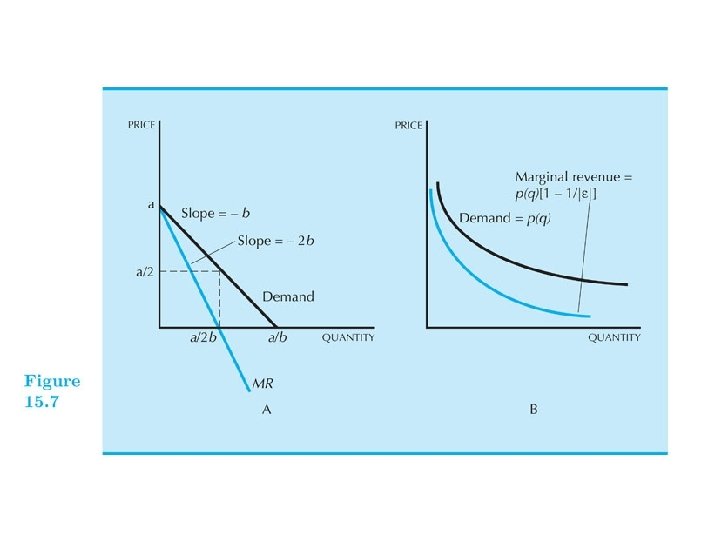
• • MR=p(1 -1/| |). When | |=1, MR=0. When | |>1, MR>0. When | |<1, MR<0.

• The intuition is, when demand is elastic, a price decrease makes quantity increase a lot. So it is worthwhile to decrease the price or increase the quantity. Hence MR>0. • On the other hand, when the demand is inelastic, a price decrease can hardly change quantity. It is not worthwhile to decrease the price or increase the quantity, so MR<0.

• • • For linear demand x=a-bp p=(a-x)/b MR =p+(dp/dx)x =p-x/b =(a-x)/b-x/b =(a-2 x)/b. So the slope is twice negative.


• Simple observation, a firm will not choose a price at which the demand is inelastic. • By decreasing the quantity or increasing price, since MR<0, decreasing the quantity increases R. • Decreasing the quantity decreases cost C. • R is increased, C is decreased, so total profit is increased.

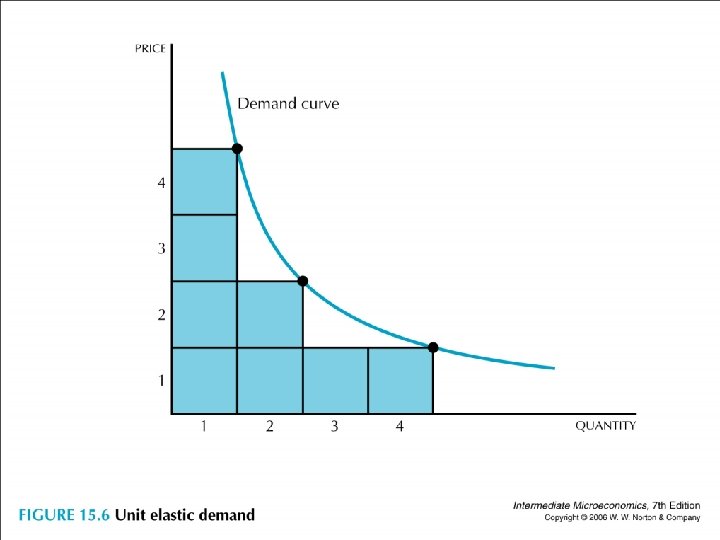
• A log-log plot is convenient. • Plot ln(x) on ln(p). • If ln(x)=c+fln(p), then dln(x)/dln(p)=(dx/x)/(dp/p)=f. • Unit elastic demand has MR=0 or R=constant. • Any rectangular under the demand curve has the same area.



• Can also work conveniently in this way. • To generate a demand of constant elasticity, we want ln(x)=k+fln(p) where k, f are constants.

• • ln(x)=k+fln(p) Let ek=c ln(x) =ln(ek)+ln(pf) =ln(cpf) xp-f=c. For instance, if unit elastic, then xp-(-1)=c or xp=c. • Work out some examples, f=-2, f=-1/2 yourself.

• Income elasticity can be similarly defined as (∆x/x)/(∆m/m). • Income elasticity>0: normal • <0: inferior • >1: luxury.

• Income elasticities tend to cluster around 1 because budget constraint is binding. • p 1 x 1 + p 2 x 2=m • p 1 x 1’+ p 2 x 2’=m’. • Let ∆ denote the difference.

• Then p 1∆ x 1+p 2∆x 2=∆m • p 1∆ x 1/∆m+ p 2∆x 2/∆m=1 • [(p 1 x 1)/m](∆ x 1/x 1)/(∆m/m)+ [(p 2 x 2)/m] (∆x 2 /x 2)/(∆m/m)=1. • The weighted average of the income elasticities is 1, where the weights are the expenditure shares.

• Chapter 15 Market Demand • Key Concept: elasticity • Elasticity measures how responsive demand is to a change. • We make it unit free by measuring the percentage of quantity change in response to a percentage change of the variable in concern.