Chapter 15 CHEMICAL EQUILIBRIUM Describing Chemical Equilibrium Chemical

Chapter 15; CHEMICAL EQUILIBRIUM Describing Chemical Equilibrium �Chemical Equilibrium—A Dynamic Equilibrium �The Equilibrium Constant �Heterogeneous Equilibria; Solvents in Homogeneous Equilibria Using the Equilibrium Constant �Qualitatively Interpreting the Equilibrium Constant �Predicting the Direction of Reaction �Calculating Equilibrium Concentrations 14 | 1

Changing Reaction Conditions: Le Châtelier’s Principle �Removing Products or Adding Reactants �Changing the Pressure and Temperature �Effect of a Catalyst

Chemical reactions often seem to stop before they are complete. Actually, such reactions are reversible. That is, the original reactants form products, but then the products react with themselves to give back the original reactants. When these two reactions—forward and reverse—occur at the same rate, a chemical equilibrium exists. 14 | 3
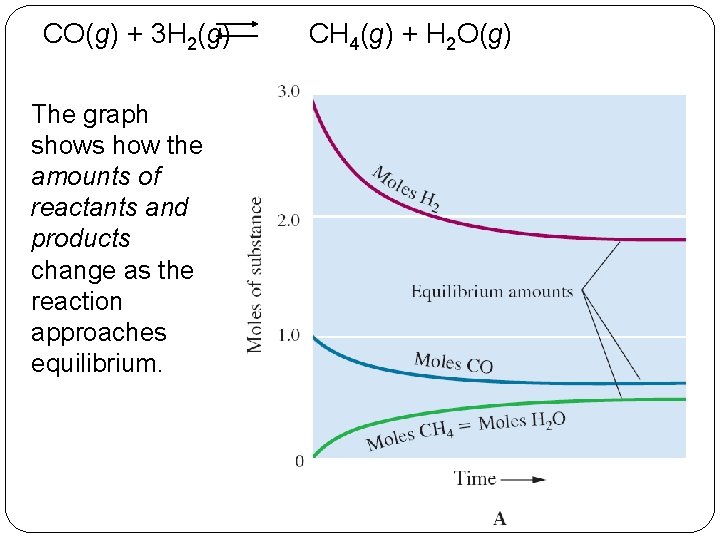
CO(g) + 3 H 2(g) The graph shows how the amounts of reactants and products change as the reaction approaches equilibrium. 14 | 4 CH 4(g) + H 2 O(g)

CO(g) + 3 H 2(g) This graph shows how the rates of the forward reaction and the reverse reaction change as the reaction approaches equilibrium. 14 | 5 CH 4(g) + H 2 O(g)

Chemical equilibrium is the state reached by a reaction mixture when the rates of the forward and reverse reactions have become equal. We can apply stoichiometry to compute the content of the reaction mixture at equilibrium. 14 | 6

When heated PCl 5, phosphorus pentachloride, forms PCl 3 and Cl 2 as follows: PCl 5(g) PCl 3(g) + Cl 2(g) When 1. 00 mol PCl 5 in a 1. 00 -L container is allowed to come to equilibrium at a given temperature, the mixture is found to contain 0. 135 mol PCl 3. What is the molar composition of the mixture? 14 | 7

We will organize this problem by using the chemical reaction to set up a table of initial, change, and equilibrium amounts. Initially we had 1. 00 mol PCl 5 and no PCl 3 or Cl 2. The change in each is stoichiometric: If x moles of PCl 5 react, then x moles of PCl 3 and x moles of Cl 2 are produced. For reactants, this amount is subtracted from the original amount; for products, it is added to the original amount. 14 | 8

PCl 5(g) Initial Change Equilibrium PCl 3(g) + Cl 2(g) 1. 00 mol 0 0 –x +x +x 1. 00 – x x x We were told that the equilibrium amount of PCl 3 is 0. 135 mol. That means x = 0. 135 mol. We can now find the amounts of the other substances. 14 | 9

The Equilibrium Constant, Kc The equilibrium constant expression for a reaction is obtained by multiplying the concentrations of products, dividing by the concentrations of reactants, and raising each concentration term to a power equal to its coefficient in the balanced chemical equation. The equilibrium constant, Kc, is the value obtained for the Kc expression when equilibrium concentrations are substituted. 14 | 10

For the reaction a. A + b. B c. C + d. D The equilibrium constant expression is Kc = 14 | 11

An example to consider; Methanol (also called wood alcohol) is made commercially by hydrogenation of carbon monoxide at elevated temperature and pressure in the presence of a catalyst: 2 H 2(g) + CO(g) CH 3 OH(g) What is the Kc expression for this reaction? 14 | 12

When we are given some information about equilibrium amounts, we are able to calculate the value of Kc. We need to take care to remember that the Kc expression uses molar concentrations. 14 | 13

Example; Carbon dioxide decomposes at elevated temperatures to carbon monoxide and oxygen: 2 CO 2(g) 2 CO(g) + O 2(g) At 3000 K, 2. 00 mol CO 2 is placed into a 1. 00 -L container and allowed to come to equilibrium. At equilibrium, 0. 90 mol CO 2 remains. What is the value of Kc at this temperature? 14 | 14
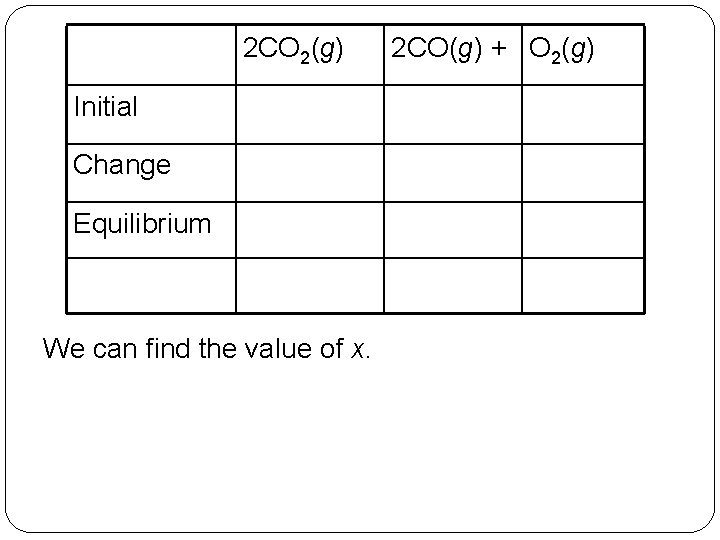
2 CO 2(g) Initial Change Equilibrium We can find the value of x. 14 | 15 2 CO(g) + O 2(g)

2 CO 2(g) 2 CO(g) + O 2(g) Next we find the concentrations of all the species at equilibrium [CO 2]= [CO]= [O 2]= We then calculate Kc by substituting the various equilibrium concentrations in the Equilibrium constant expression. 14 | 16

In a heterogeneous equilibrium, in the Kc expression, the concentrations of solids and pure liquids are constant (due to these substances’ constant density). As a result, we incorporate those constants into the value of Kc, thereby making a new constant, Kc. In other words, equilibrium is not affected by solids and pure liquids as long as some of each is present. More simply, we write the Kc expression by replacing the concentration of a solid or pure liquid with 1. 14 | 17
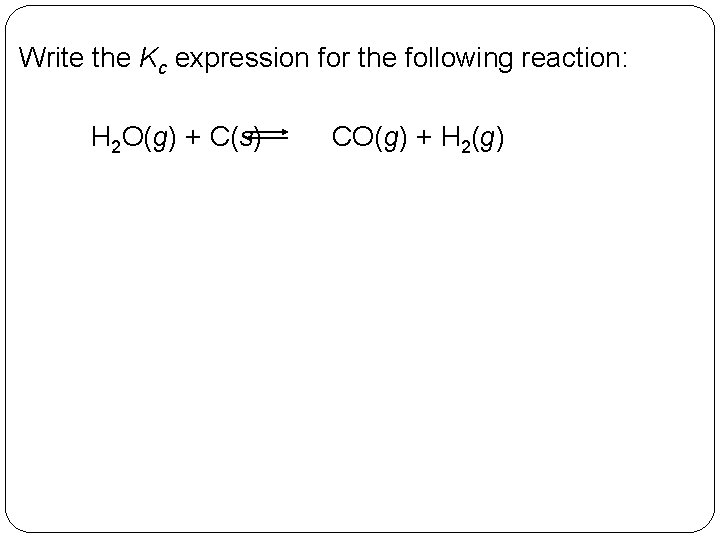
Write the Kc expression for the following reaction: H 2 O(g) + C(s) 14 | 18 CO(g) + H 2(g)

Given: a. A + b. B c. C + d. D; K 1 When the reaction is reversed: c. C + d. D a. A + b. B; K 2 The equilibrium constant expression is inverted: K 2 = 14 | 19

Given: a. A + b. B c. C + d. D; K 1 When the reaction is doubled: 2 a. A + 2 b. B 2 c. C + 2 d. D; K 2 The equilibrium constant expression, K 2 , is the square of the equilibrium constant expression, K 1: K 2 = 14 | 20

For the reaction a. A(g) + b. B(g) c. C(g) + d. D(g) The equilibrium constant expressions are Kc = 14 | 21 and Kp =
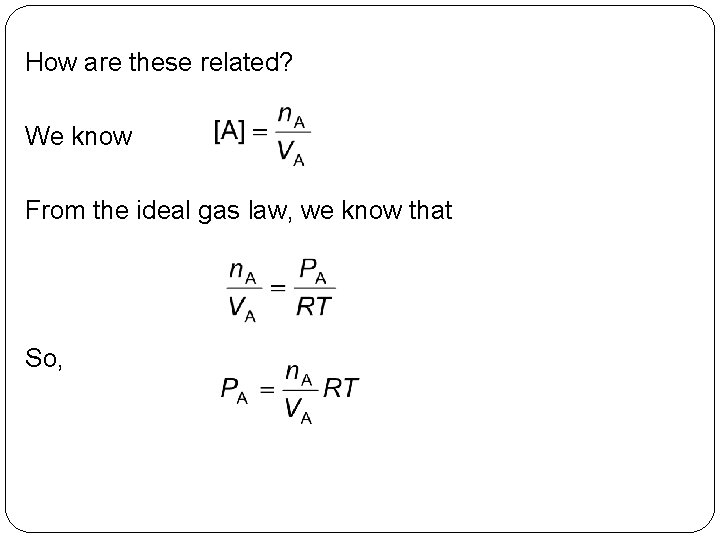
How are these related? We know From the ideal gas law, we know that So, 14 | 22

When you express an equilibrium constant for a gaseous reaction in terms of partial pressures, you call it the equilibrium constant, Kp In general, the value of Kp is different from that of Kc. We will explore this relationship on the next slides. Recall the ideal gas law and the relationship between pressure and molarity of a gas: 14 | 23
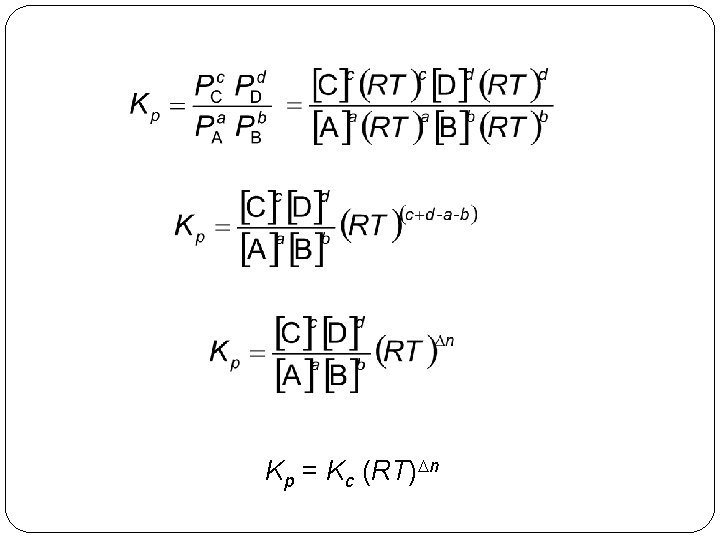
Kp = Kc (RT)Dn 14 | 24
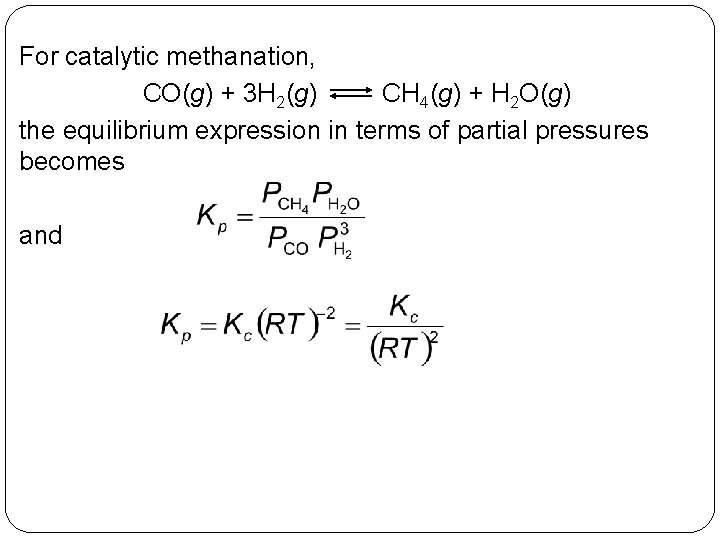
For catalytic methanation, CO(g) + 3 H 2(g) CH 4(g) + H 2 O(g) the equilibrium expression in terms of partial pressures becomes and 14 | 25

Example; The value of Kc at 227°C is 0. 0952 for the following reaction: CH 3 OH(g) CO(g) + 2 H 2(g) What is Kp at this temperature? R = 0. 08206 L atm/(mol K) 14 | 26

We can use the value of the equilibrium constant in several ways. First, we can qualitatively describe the content of the reaction mixture by looking at the magnitude of Kc. Second, we can determine the direction in which a reaction will proceed by comparing Kc to the value of the reaction quotient, Q, which has the same expression as Kc but uses nonequilibrium values. Finally, we can determine equilibrium concentrations given the initial concentrations and the value of Kc. 14 | 27

When Kc is very large (>102), the equilibrium mixture is mostly products. When Kc is very small (<10 -2), the equilibrium mixture is mostly reactants. When Kc approaches 1, the equilibrium mixture contains appreciable amounts of both reactants and products. 14 | 28

Kc = 0. 82 for a reaction. Describe the composition of the equilibrium mixture. 14 | 29

Reaction Quotient, Q The reaction quotient has the same form as the equilibrium constant, but uses initial concentrations for its value. When Kc > Q, the reaction proceeds to the right. When Kc < Q, the reaction proceeds to the left. When Kc = Q, the reaction is at equilibrium. 14 | 30
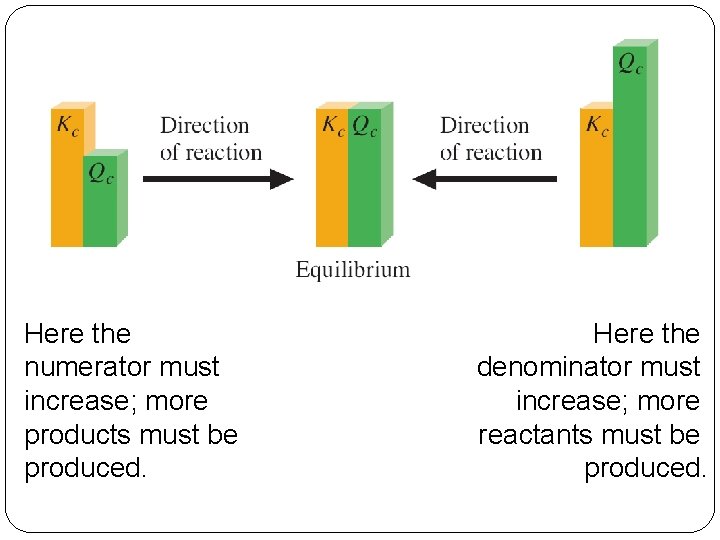
� Qc must move toward Kc. Here the numerator must increase; more products must be produced. 14 | 31 Here the denominator must increase; more reactants must be produced.
- Slides: 31