Chapter 14 Waiting Lines and Queuing Theory Models

Chapter 14 Waiting Lines and Queuing Theory Models Prepared by Lee Revere and John Large To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -1 1

Learning Objectives Students will be able to: 1. Describe the trade-off curves for cost-of-waiting time and cost-of-service. 2. Understand the three parts of a queuing system: the calling population, the queue itself, and the service facility. 3. Describe the basic queuing system configurations. 4. Understand the assumptions of the common models dealt with in this chapter. 5. Analyze a variety of operating characteristics of waiting lines. To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -2 2

Chapter Outline 14. 1 Introduction 14. 2 Waiting Line Costs 14. 3 Characteristics of a Queuing System 14. 4 Single-Channel Queuing Model with Poisson Arrivals and Exponential Service Times 14. 5 Multiple-Channel Queuing Model with Poisson Arrivals and Exponential service Times To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -3 3

Chapter Outline (continued) 14. 6 Constant Service Time Model 14. 7 Finite Population Model 14. 8 Some General Operating Characteristics Relationships 14. 9 More Complex Queuing Models and the Use of Simulation To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -4 4

Introduction Queuing theory is one of the most widely used quantitative analysis techniques. The three basic components are: § Arrivals § Service facilities § Actual waiting line To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -5 5

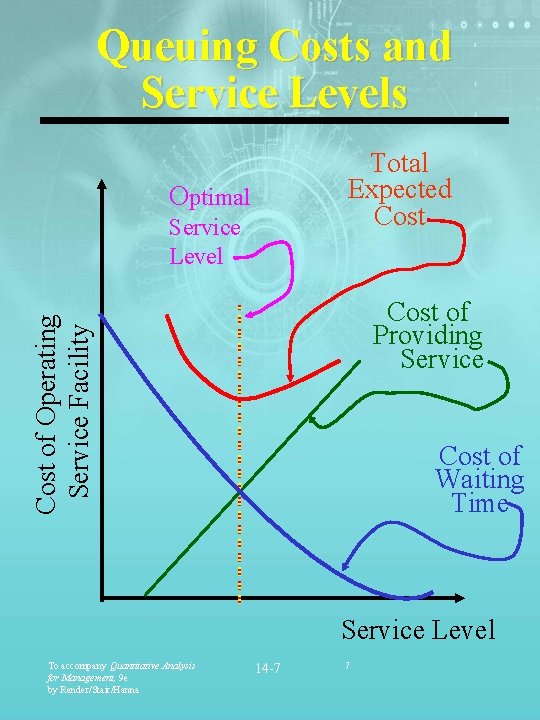
Waiting Line Costs Queuing analysis includes: § Determining the best level of service for an organization. § Analyzing the trade-off between cost of providing service and cost of waiting time. § Finding the service level that minimizes the total expected cost. To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -6 6

Queuing Costs and Service Levels Total Expected Cost Optimal Service Level Cost of Operating Service Facility Cost of Providing Service Cost of Waiting Time Service Level To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -7 7

Three Rivers Shipping: Waiting Line Cost Analysis The superintendent at Three Rivers Shipping Company wants to determine the optimal number of stevedores to employ each shift. Number of Stevedore Teams 1 2 3 4 Avg. number of ships arriving per shift Average waiting time per ship 5 5 7 4 3 2 35 20 15 10 Total ship hours lost Est. cost per hour of idle ship time $1, 000 Value of ships' lost time 35, 000 29, 000 $15, 000 $10, 000 Stevedore teams salary Total Expected Cost To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna $1, 000 $6, 000 $12, 000 18, 000 $24, 000 $41, 000$32, 000 $33, 000 $34, 000 14 -8 8

Characteristics of a Queuing System § Arrival Characteristics ØSize of the calling population ØPattern of arrivals ØBehavior of arrivals § Waiting Line Characteristics ØQueue length ØQueue discipline § Service Facility Characteristics ØConfiguration of the queuing system ØService time distribution To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -9 9

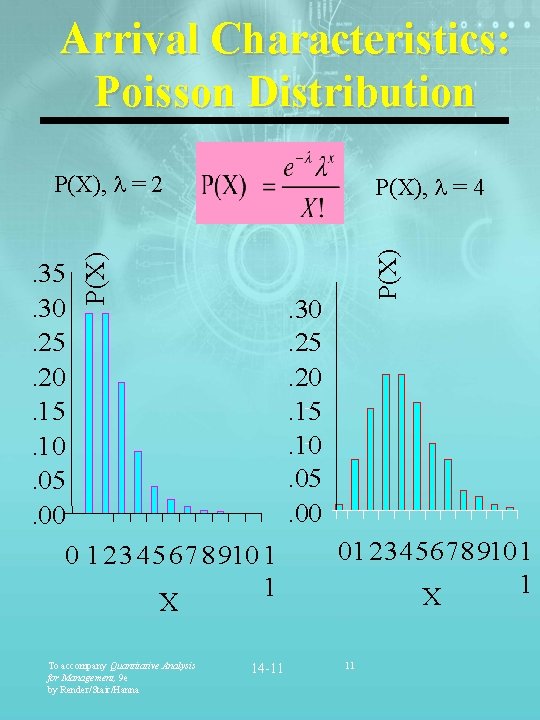
Arrival Characteristics of a Queuing System § Calling Population: Ø Unlimited (infinite) Ø Limited (finite) § Arrival Pattern Ø Randomly Ø Poisson Distribution To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -10 10

Arrival Characteristics: Poisson Distribution P(X), = 2 . 35. 30. 25. 20. 15. 10. 05. 00 0 1 2 3 45 6 7 8 910 1 1 X To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -11 P(X), = 4 . 30. 25. 20. 15. 10. 05. 00 012345678910 1 1 X 11

Arrival Characteristics of a Queuing System (continued) Behavior of arrivals: § Join the queue, and wait till served. § Balk; refuse to join the line. § Renege; leave the line. To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -12 12

Waiting Line Characteristics of a Queuing System Waiting Line Characteristics: § Length of the queue Ø Limited Ø Unlimited (assumed) § Service priority/Queue discipline Ø FIFO (assumed) Ø Other To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -13 13

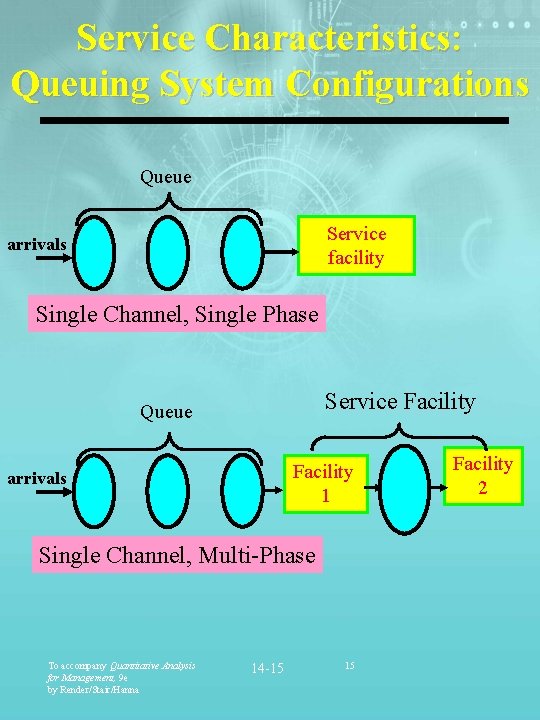
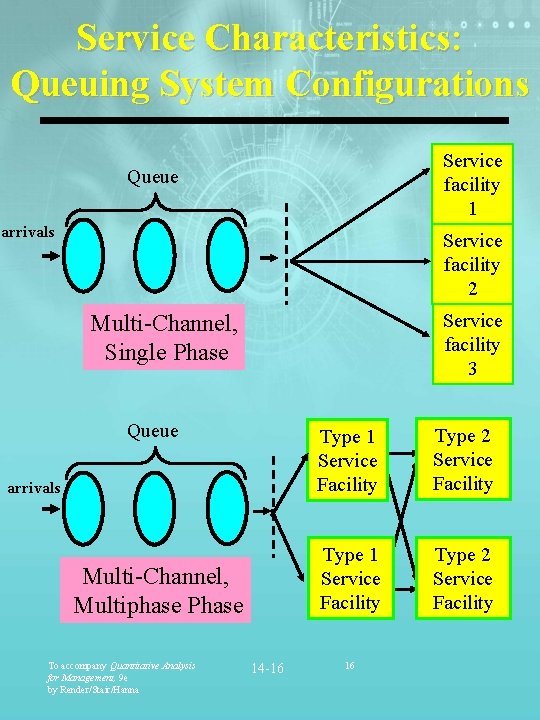
Waiting Line Characteristics of a Queuing System (continued) Service Facility Characteristics § Number of channels (servers) Ø Single Ø Multiple § Number of phases in service system (customer stations) Ø Single (1 stop) Ø Multiple (2+ stops) § Service time distribution Ø Negative exponential Ø Other To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -14 14

Service Characteristics: Queuing System Configurations Queue Service facility arrivals Single Channel, Single Phase Service Facility Queue Facility 1 arrivals Single Channel, Multi-Phase To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -15 15 Facility 2

Service Characteristics: Queuing System Configurations Service facility 1 Queue arrivals Service facility 2 Service facility 3 Multi-Channel, Single Phase Queue arrivals Multi-Channel, Multiphase Phase To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -16 Type 1 Service Facility Type 2 Service Facility 16

Service Characteristics of a Queuing System Service Time Patterns: § Negative exponential probability distribution § Other distribution To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -17 17

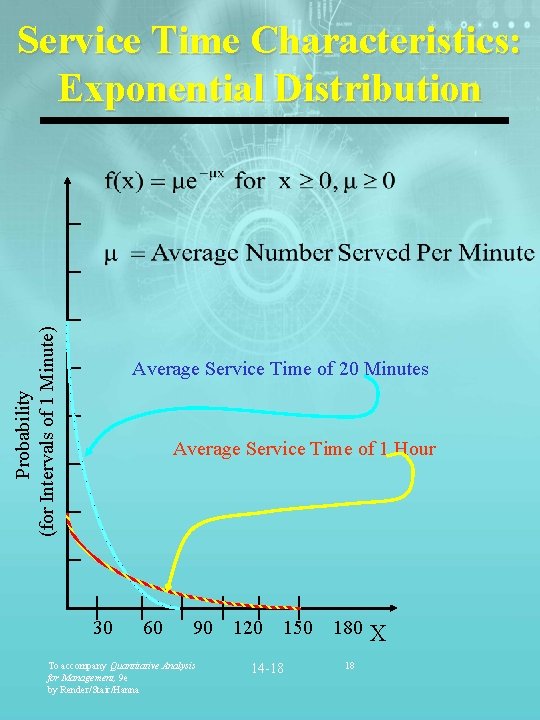
Probability (for Intervals of 1 Minute) Service Time Characteristics: Exponential Distribution Average Service Time of 20 Minutes Average Service Time of 1 Hour 30 60 90 To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 120 150 14 -18 180 18 X

Kendall Notation for Queuing Models Kendall notation consists of a basic three-symbol form. Arrival Service Time Number of Service Distribution Channels Open Where, M = Poisson distribution for the number of occurrences (or exponential times) D = Constant (deterministic rate) G = General distribution with mean and variance known M/M/2 To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna Single channel with Poisson arrivals and exponential service times and two channels 14 -19 19

Assumptions: M/M/1 Model 1. Queue discipline: FIFO 2. No balking or reneging 3. Independent arrivals; constant rate over time 4. Arrivals: Poisson distributed 5. Service times: average known 6. Service times: negative exponential 7. Average service rate > average arrival rate To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -20 20

Operating Characteristics of Queuing Systems § Average time each customer spends in the queue § Average length of the queue § Average time each customer spends in the system § Average number of customers in the system § Probability that the service facility will be idle § Utilization factor for the system § Probability of a specific number of customers in the system To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -21 21

Operating Characteristic Equations: M/M/1 Probability the number of customers is > k, To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -22 22

Car Wash Example: M/M/1 § Assume you are planning a car wash to raise money for a local charity. § You anticipate the cars arriving in a single line and being serviced by one team of washers. § Based on historical data, you believe cars will arrive every 30 minutes, and the team can wash a car in about 20 minutes. § The arrival rates follow a Poisson distribution and the service rates are exponentially distributed. § What are the operating characteristics for this system? To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -23 23

Car Wash Example: Operating Characteristics = 2 cars arriving per hour u = 3 cars serviced per hour L W => => Lq Wq Pw => => => Po => ? cars in the system on average ? hour that an average car spends in the system ? cars waiting on average ? hours is average wait ? percent of time car washers are busy ? probability that there are 0 cars in the system To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -24 24

Car Wash Example: Operating Characteristics Solution = 2 cars arriving per hour u = 3 cars serviced per hour L = 2/(3 -2) => 2 cars in the system on average W = 1/(3 -2) => 1 hour that an average car spends in the system Lq = 2^2/3(3 -2) => 1. 33 cars waiting on average Wq = 2/3(3 -2) =>. 67 hours is average wait Pw = 2/3 =>. 67 percent of time washers are busy P(0) = 1 – (2/3) =>. 33 probability that there are 0 cars in the system To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -25 25

Operating Characteristic Equations: M/M/m Probability there are no customers in the system, P 0 = 1 é n = M -1 1 æ l ö n ù 1 æ l ö M Mm çç ÷÷ ú + çç ÷÷ ê å êë n = 0 n! è m ø úû M ! è m ø Mm - l Average number of customers in the system, lm æç l m ö÷ M l è ø L= P 0 + 2 m (M - 1)( ! Mm - l ) To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -26 26

Operating Characteristic Equations: M/M/m The average time a customer spends in the system, W= The average number of customers in line waiting, l Lq = L m The average time a customer spends in the queue waiting for service, l Wq = W - 1 m = l r= Mm The utilization rate, To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna L 14 -27 27 Lq l

Car Wash Example: M/M/2 Should you have 2 teams of car washers? ? ? = 2 cars/ hr P(0) = L= u = 3 cars/ hr 1 1+2+14 6 3 2 9 6 -2 2 3 2/3 1! 2 3 -2 2 2 1 2 + 2 3 = 1 = 0. 5 2 = 3 = 0. 75 4 W = 0. 75 = 3 = 22. 5 minutes 2 4 Lq = 0. 75 – 2 = 1 = 0. 083 3 12 Wq = 0. 083 = 0. 0415 hour = 2. 5 minutes 2 To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -28 28

Operating Characteristic Equations: M/D/1 Average length of the queue, Average waiting time in the queue, Average number of customers in the queue, Lq = 2 m(m - l) Wq = l 2 m(m - l) L = Lq + l m W=Wq + Average time in the system, To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna l 2 14 -29 29 1 m

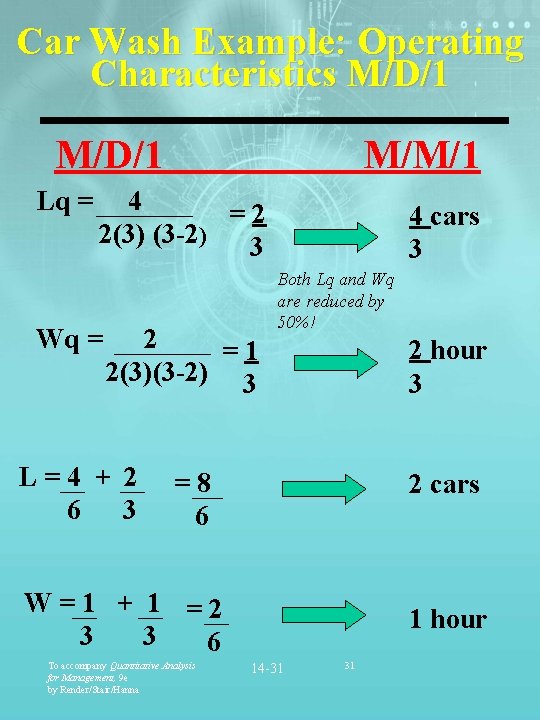
Car Wash Example: M/D/1 1. Your charity is considering purchasing an automatic car wash system. 2. Cars will continue to arrive according to a Poisson distribution, with 2 cars arriving every hour. 3. However, the service time will now be constant with a rate of 3 cars per hour. Compare the operating characteristics of this model with your previous models. To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -30 30

Car Wash Example: Operating Characteristics M/D/1 Lq = M/M/1 4 =2 2(3) (3 -2) 3 Wq = 2 =1 2(3)(3 -2) 3 L=4 + 2 6 3 4 cars 3 Both Lq and Wq are reduced by 50%! 2 hour 3 =8 6 2 cars W=1 + 1 =2 3 3 6 To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 1 hour 14 -31 31

Operating Characteristic Equations: M/M/1 - Finite Source The probability that the system is empty, P 0 = 1 N! æ l ö å= ( N - n)! çç m ÷÷ è ø n 0 N n The average length of the queue, æl +m ö ÷(1 - P 0 ) Lq = N - ç è l ø The average number of customers in the system, L = Lq + (1 - P 0 ) To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -32 32

Operating Characteristic Equations: M/M/1 - Finite Source The average waiting time in the queue, Lq Wq = (N - L )l The average waiting time in the system, W = Wq + 1 m Probability of n units in the system, n N! æ l ö çç ÷÷ P 0 P(n, n £ N) = Pn = (N - n )! è m ø To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -33 33

Department of Commerce Example: M/M/1 – finite source 1. The Department of Commerce has 5 printers that each need repair after about 20 hours of work. Breakdowns follow a Poisson distribution. 2. The technician can service a printer in an average of about 2 hours, following an exponential distribution. Determine the operating characteristics for this model. To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -34 34

Operating Characteristics M/M/1 Finite source = 1/20 = 0. 05 printer/ hr. u = ½ = 0. 50 printer/ hr. Po = 5 ∑ n=0 1 5! 0. 05 n (5 -n)! 0. 5 = 0. 564 Lq = 5 - 0. 05 + 0. 5 (1 -Po) = 5 – 4. 8 = 0. 2 0. 05 L = 0. 2 + (1 -0. 564) = 0. 64 printer Wq = 0. 2 (5 -0. 64)(0. 05) = 0. 91 hour W = 0. 91 + 1 = 2. 91 hours 0. 50 To accompany Quantitative Analysis 14 -35 for Management, 9 e by Render/Stair/Hanna 35

General Operating Characteristic Relationships After reaching a steady state, certain relationships exist among specific operating characteristics. To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -36 36

Complex Queuing Models and Simulation Computer simulation is used to handle many realworld queuing applications that are complex. Simulation allows: § Analysis of controllable factors § Approximation of the actual service system To accompany Quantitative Analysis for Management, 9 e by Render/Stair/Hanna 14 -37 37