Chapter 14 Sound Sound waves Sound longitudinal waves

Chapter 14 Sound

Sound waves • Sound – longitudinal waves in a substance (air, water, metal, etc. ) with frequencies detectable by human ears (between ~ 20 Hz and ~ 20 KHz) • Ultrasound – longitudinal waves in a substance (air, water, metal, etc. ) with frequencies higher than detectable by human ears (> 20 KHz) • Infrasound – longitudinal waves in a substance (air, water, metal, etc. ) with frequencies lower than detectable by human ears (< 20 Hz)

Speed of sound • Speed of sound: ρ – density of a medium, B – bulk modulus of a medium • Traveling sound waves

Rate of energy transmission • As the wave travels it transports energy, even though the particles of the medium don’t propagate with the wave • The average power of energy transmission for the sinusoidal solution of the wave equation • Exact expression depends on the medium or the system through which the wave is propagating

Intensity of sound • Intensity of sound – average rate of sound energy transmission per unit area • For a sinusoidal traveling wave: • Decibel scale β – sound level; I 0 = 10 -12 W/m 2 – lower limit of human hearing

Chapter 14 Problem 12 Two sounds have measured intensities of I 1 = 100 W/m 2 and I 2 = 200 W/m 2. By how many decibels is the level of sound 1 lower than that of sound 2?

Sound from a point source • Point source – source with size negligible compared to the wavelength • Point sources produce spherical waves • Wavefronts – surfaces over which oscillations have the same value • Rays – lines perpendicular to wavefronts indicating direction of travel of wavefronts

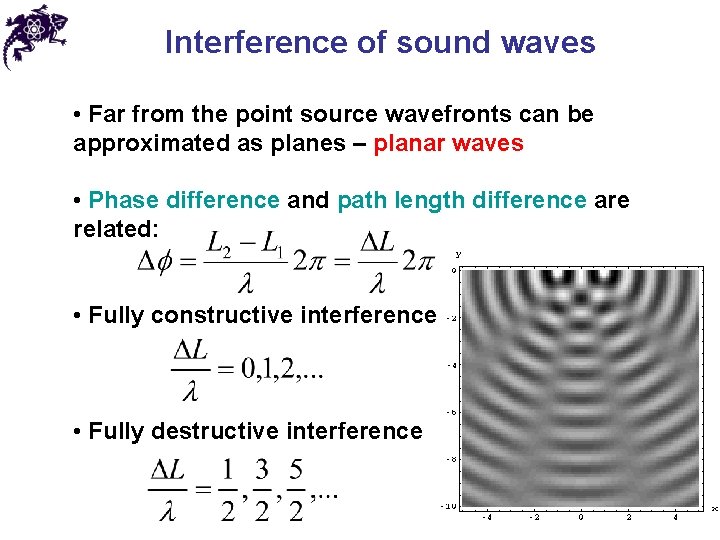
Interference of sound waves • Far from the point source wavefronts can be approximated as planes – planar waves • Phase difference and path length difference are related: • Fully constructive interference • Fully destructive interference

Variation of intensity with distance • A single point emits sound isotropically – with equal intensity in all directions (mechanical energy of the sound wave is conserved) • All the energy emitted by the source must pass through the surface of imaginary sphere of radius r • Sound intensity (inverse square law)

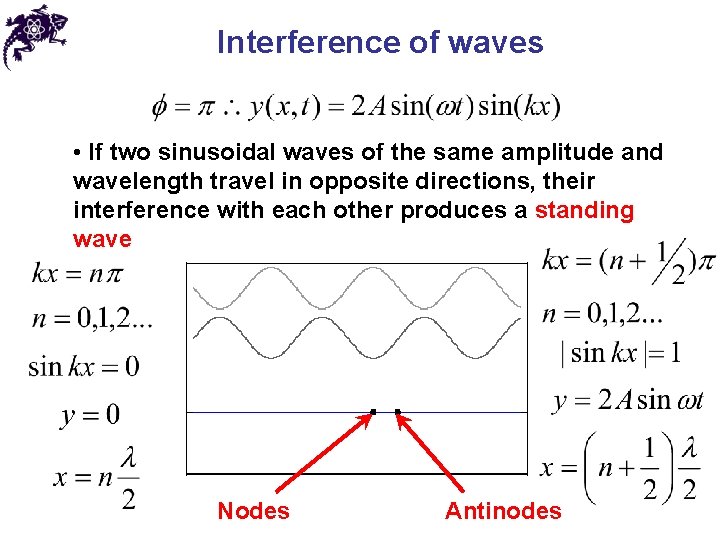
Interference of waves • Considering two sinusoidal waves of the same amplitude, wavelength, but running in opposite directions • The resultant wave:

Interference of waves • If two sinusoidal waves of the same amplitude and wavelength travel in opposite directions, their interference with each other produces a standing wave Nodes Antinodes

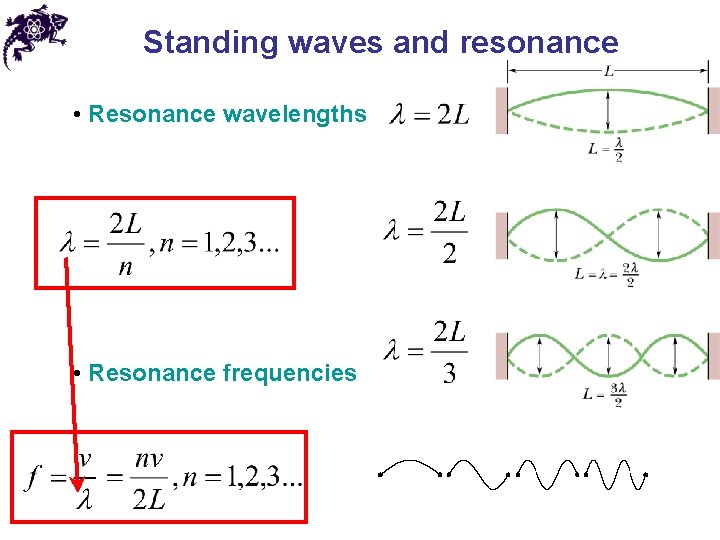
Standing waves and resonance • For a medium with fixed boundaries (hard reflection) standing waves can be generated because of the reflection from both boundaries: resonance • Depending on the number of antinodes, different resonances can occur

Standing waves and resonance • Resonance wavelengths • Resonance frequencies

Harmonic series • Harmonic series – collection of all possible modes resonant oscillations (n – harmonic number) • First harmonic (fundamental mode):

Chapter 14 Problem 38 Two pieces of steel wire with identical cross sections have lengths of L and 2 L. The wires are each fixed at both ends and stretched so that the tension in the longer wire is four times greater than in the shorter wire. If the fundamental frequency in the shorter wire is 60 Hz, what is the frequency of the second harmonic in the longer wire?

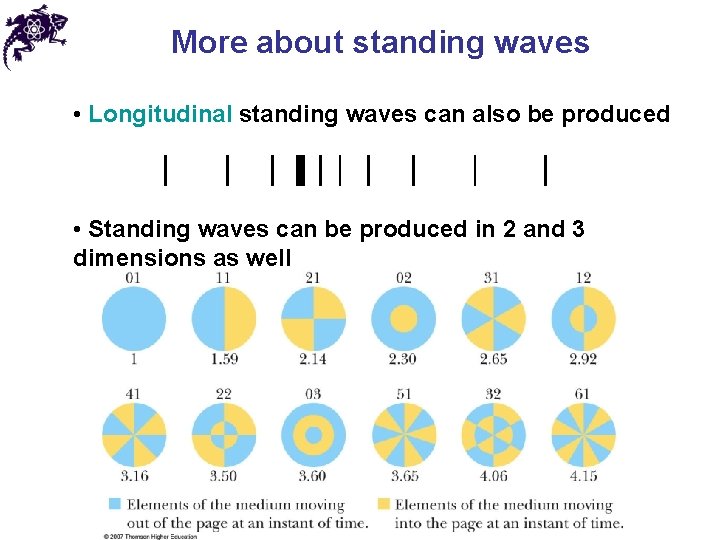
More about standing waves • Longitudinal standing waves can also be produced • Standing waves can be produced in 2 and 3 dimensions as well

More about standing waves • Longitudinal standing waves can also be produced • Standing waves can be produced in 2 and 3 dimensions as well

Sources of musical sound • Music produced by musical instruments is a combination of sound waves with frequencies corresponding to a superposition of harmonics (resonances) of those musical instruments • In a musical instrument, energy of resonant oscillations is transferred to a resonator of a fixed or adjustable geometry

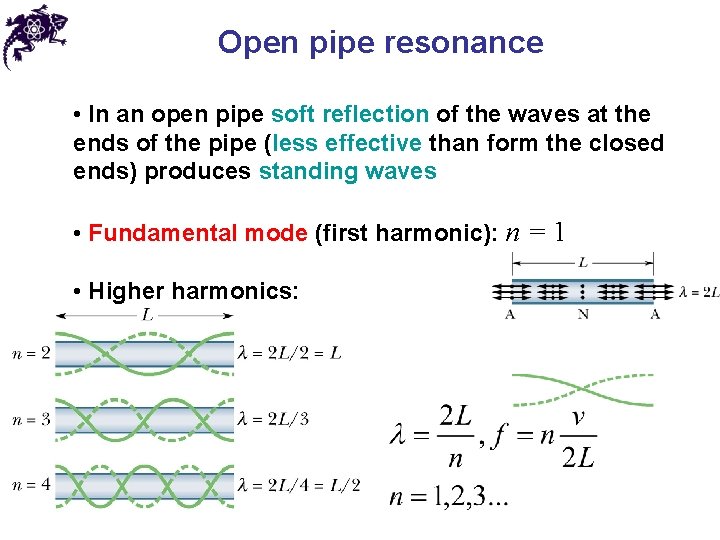
Open pipe resonance • In an open pipe soft reflection of the waves at the ends of the pipe (less effective than form the closed ends) produces standing waves • Fundamental mode (first harmonic): n = 1 • Higher harmonics:

Organ pipes • Organ pipes are open on one end and closed on the other • For such pipes the resonance condition is modified:

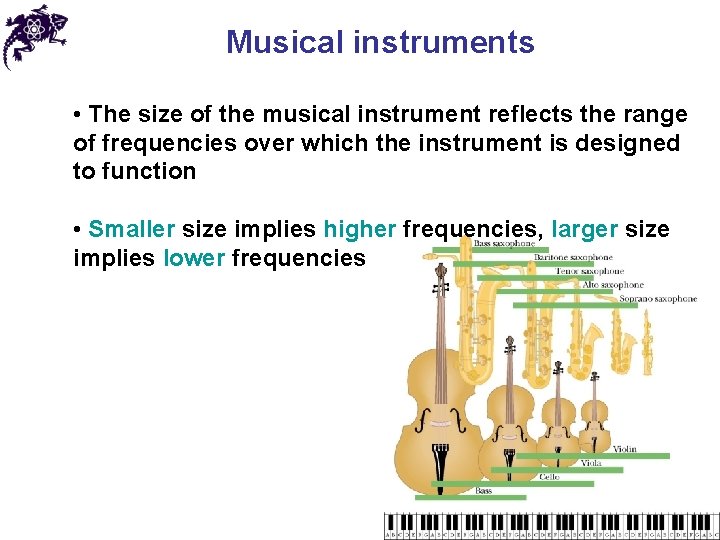
Musical instruments • The size of the musical instrument reflects the range of frequencies over which the instrument is designed to function • Smaller size implies higher frequencies, larger size implies lower frequencies

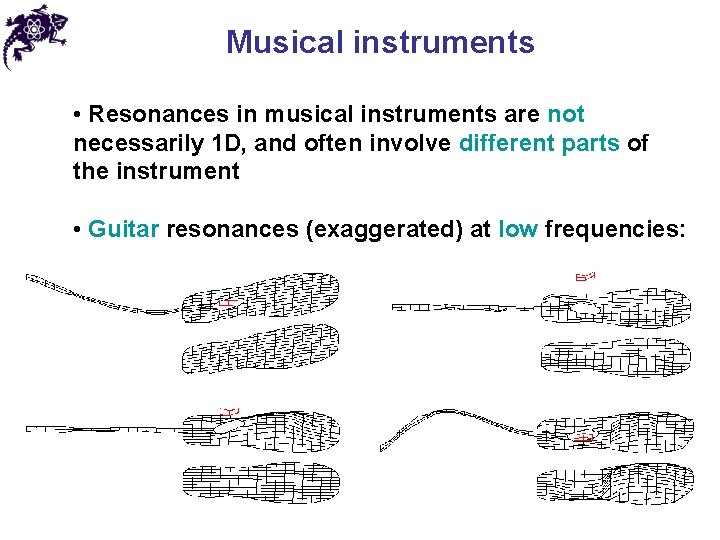
Musical instruments • Resonances in musical instruments are not necessarily 1 D, and often involve different parts of the instrument • Guitar resonances (exaggerated) at low frequencies:

Musical instruments • Resonances in musical instruments are not necessarily 1 D, and often involve different parts of the instrument • Guitar resonances at medium frequencies:

Musical instruments • Resonances in musical instruments are not necessarily 1 D, and often involve different parts of the instrument • Guitar resonances at high frequencies:

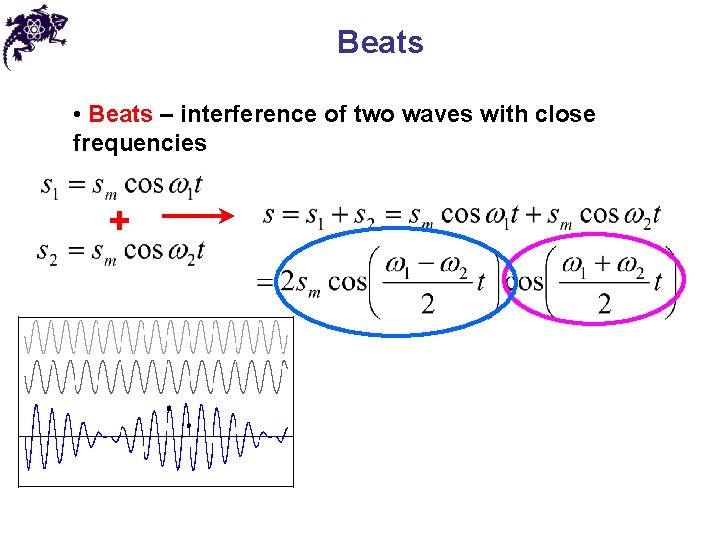
Beats • Beats – interference of two waves with close frequencies +

Doppler effect • Doppler effect – change in the frequency due to relative motion of a source and an observer (detector) Andreas Christian Johann Doppler (1803 -1853)

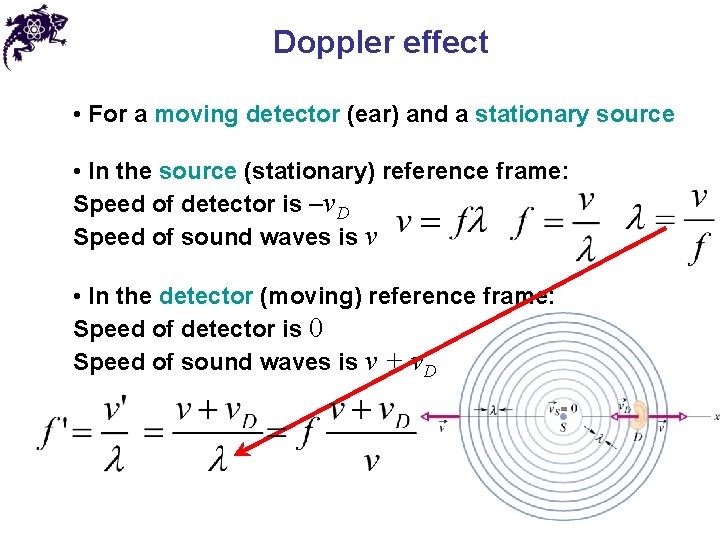
Doppler effect • For a moving detector (ear) and a stationary source • In the source (stationary) reference frame: Speed of detector is –v. D Speed of sound waves is v • In the detector (moving) reference frame: Speed of detector is 0 Speed of sound waves is v + v. D

Doppler effect • For a moving detector (ear) and a stationary source • If the detector is moving away from the source: • For both cases:

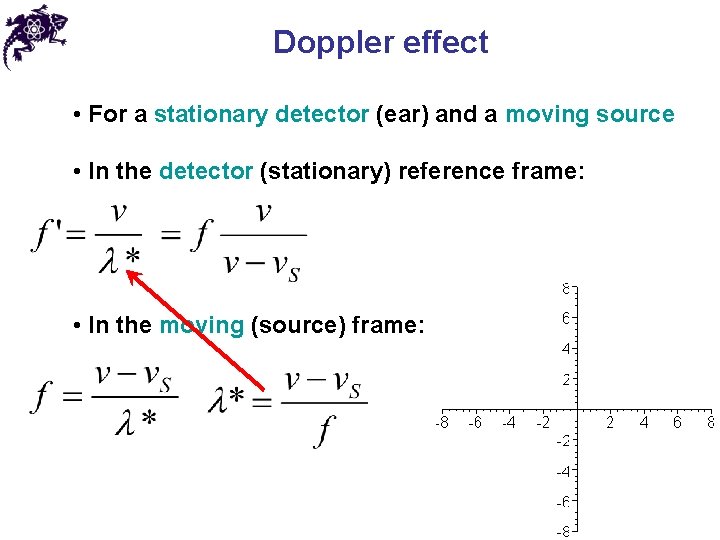
Doppler effect • For a stationary detector (ear) and a moving source • In the detector (stationary) reference frame: • In the moving (source) frame:

Doppler effect • For a stationary detector and a moving source • If the source is moving away from the detector: • For both cases:

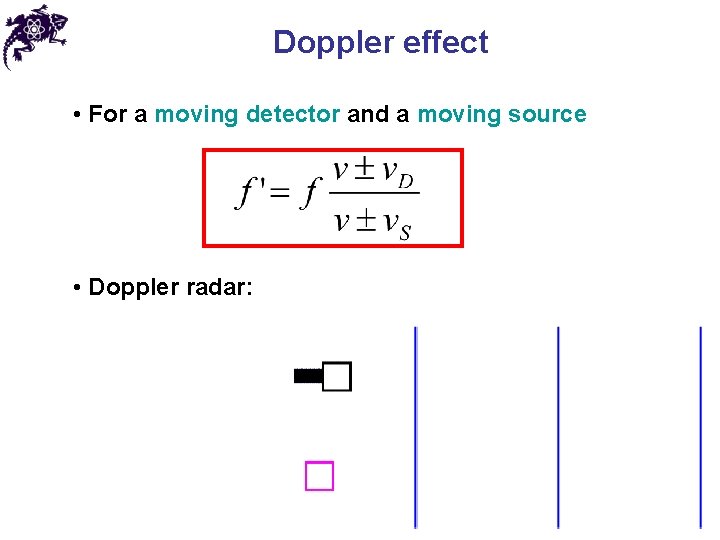
Doppler effect • For a moving detector and a moving source • Doppler radar:

Chapter 14 Problem 27 A tuning fork vibrating at 512 Hz falls from rest and accelerates at 9. 80 m/s 2. How far below the point of release is the tuning fork when waves of frequency 485 Hz reach the release point? Take the speed of sound in air to be 340 m/s.

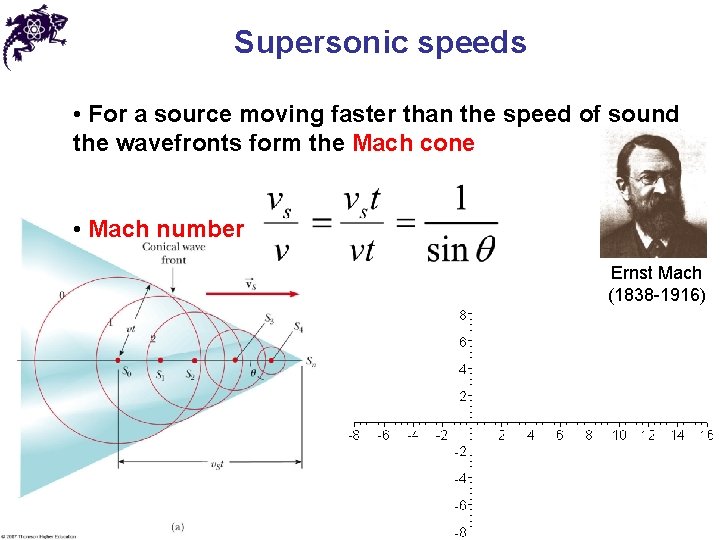
Supersonic speeds • For a source moving faster than the speed of sound the wavefronts form the Mach cone • Mach number Ernst Mach (1838 -1916)

Questions?

Answers to the even-numbered problems Chapter 14 Problem 34 824. 0 N