Chapter 14 Searching and Sorting Java Programming From

Chapter 14: Searching and Sorting Java Programming: From Problem Analysis to Program Design, Fourth Edition Java Programming: From Problem Analysis to Program Design,

Chapter Objectives s Learn how to implement the sequential search algorithm. s Explore how to sort an array using bubble sort, selection sort, and insertion sort algorithms. s Learn how to implement the binary search algorithm. s Become aware of the class Vector. s Learn more about manipulating strings using the class String. Java Programming: From Problem Analysis to Program Design, Second Edition 2

List Processing s List: A set of values of the same type. s Basic operations performed on a list: s s Search list for given item. Sort list. Insert item in list. Delete item from list. Java Programming: From Problem Analysis to Program Design, Second Edition 3

Search s Necessary components to search a list: s Array containing the list. s Length of the list. s Item for which you are searching. s After search completed: s If item found, report “success” and return location in array. s If item not found, report “failure. ” Java Programming: From Problem Analysis to Program Design, Second Edition 4

Search public static int seq. Search(int[] list, int list. Length, int search. Item) { int loc; boolean found = false; for (loc = 0; loc < list. Length; loc++) if (list[loc] == search. Item) { found = true; break; } if (found) return loc; else return -1; } Java Programming: From Problem Analysis to Program Design, Second Edition 5

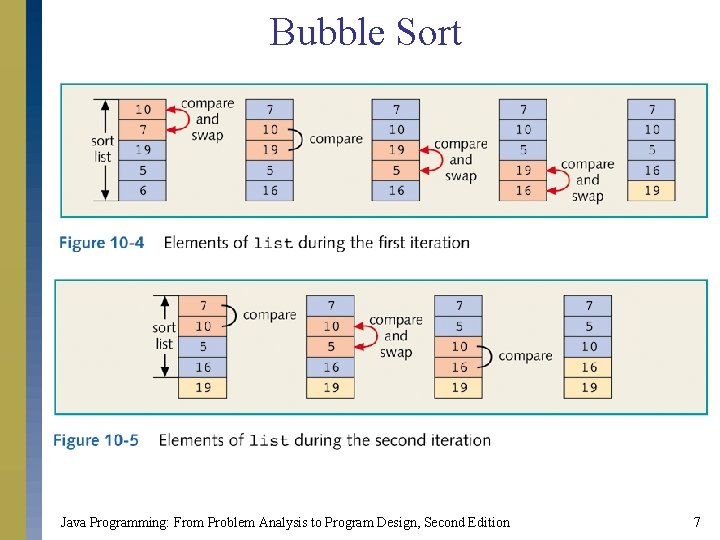
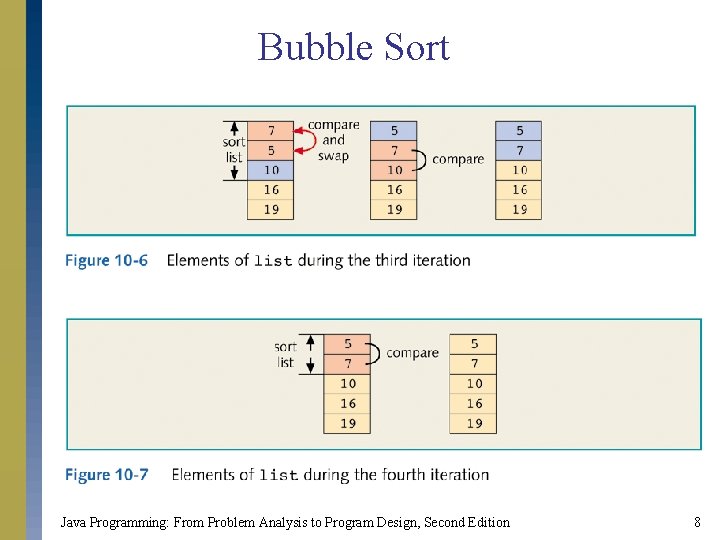
Sorting a List Bubble sort s Suppose list[0. . . n - 1] is a list of n elements, indexed 0 to n - 1. We want to rearrange (sort) the elements of list in increasing order. The bubble sort algorithm works as follows: s In a series of n - 1 iterations, the successive elements, list[index] and list[index + 1], of list are compared. If list[index] is greater than list[index + 1], then the elements list[index] and list[index + 1] are swapped (interchanged). Java Programming: From Problem Analysis to Program Design, Second Edition 6

Bubble Sort Java Programming: From Problem Analysis to Program Design, Second Edition 7

Bubble Sort Java Programming: From Problem Analysis to Program Design, Second Edition 8

Bubble Sort public static void bubble. Sort(int list[], int list. Length) { int temp; int counter, index; for (counter = 0; counter < list. Length - 1; counter++) { for (index = 0; index < list. Length - 1 – counter; index++) if (list[index] > list[index + 1]) { temp = list[index]; list[index] = list[index + 1]; list[index + 1] = temp; } } } Java Programming: From Problem Analysis to Program Design, Second Edition 9

Bubble Sort s For a list of length n, an average bubble sort makes n(n – 1) / 2 key comparisons and about n(n – 1) / 4 item assignments. s Therefore, if n = 1000, bubble sort makes about 500, 000 key comparisons and about 250, 000 item assignments to sort the list. Java Programming: From Problem Analysis to Program Design, Second Edition 10

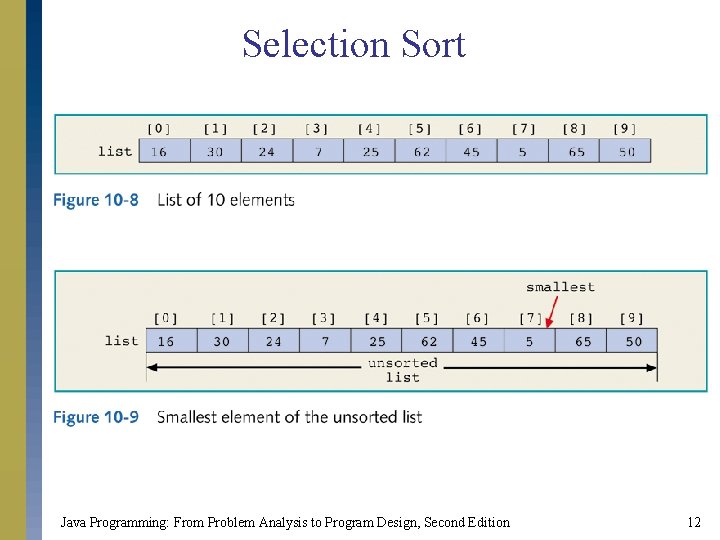
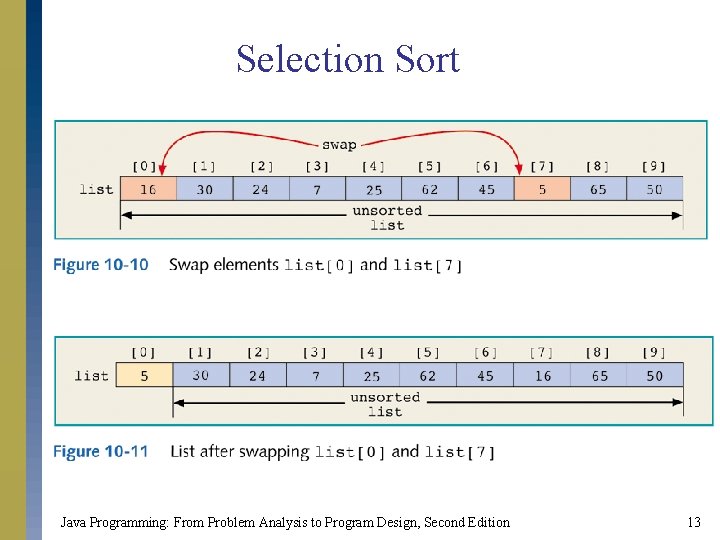
Selection Sort s List is sorted by selecting list element and moving it to its proper position. s Algorithm finds position of smallest element and moves it to top of unsorted portion of list. s Repeats process above until entire list is sorted. Java Programming: From Problem Analysis to Program Design, Second Edition 11

Selection Sort Java Programming: From Problem Analysis to Program Design, Second Edition 12

Selection Sort Java Programming: From Problem Analysis to Program Design, Second Edition 13

Selection Sort public static void selection. Sort(int[] list, int list. Length) { int index; int smallest. Index; int min. Index; int temp; for (index = 0; index < list. Length – 1; index++) { smallest. Index = index; for (min. Index = index + 1; min. Index < list. Length; min. Index++) if (list[min. Index] < list[smallest. Index]) smallest. Index = min. Index; temp = list[smallest. Index]; list[smallest. Index] = list[index]; list[index] = temp; } } Java Programming: From Problem Analysis to Program Design, Second Edition 14

Selection Sort s For a list of length n, an average selection sort makes n(n – 1) / 2 key comparisons and 3(n – 1) item assignments. s Therefore, if n = 1000, selection sort makes about 500, 000 key comparisons and about 3000 item assignments to sort the list. Java Programming: From Problem Analysis to Program Design, Second Edition 15

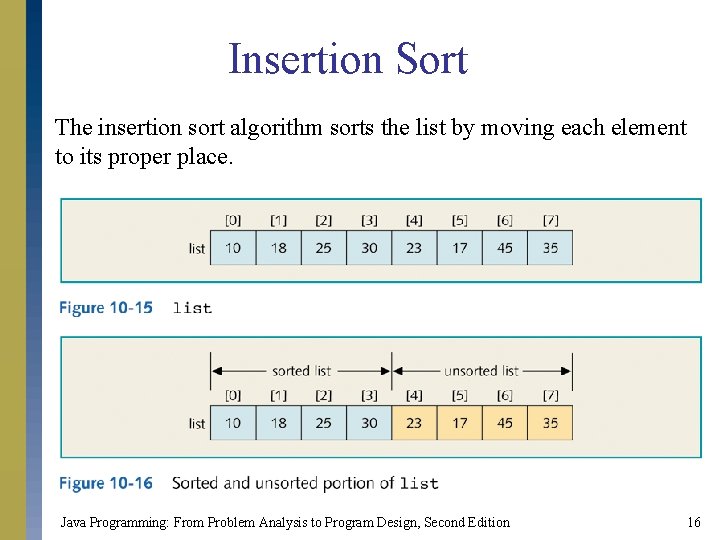
Insertion Sort The insertion sort algorithm sorts the list by moving each element to its proper place. Java Programming: From Problem Analysis to Program Design, Second Edition 16

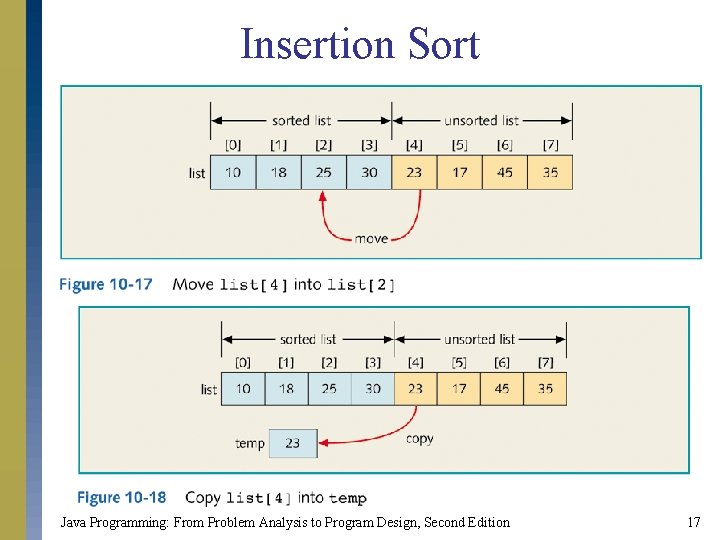
Insertion Sort Java Programming: From Problem Analysis to Program Design, Second Edition 17

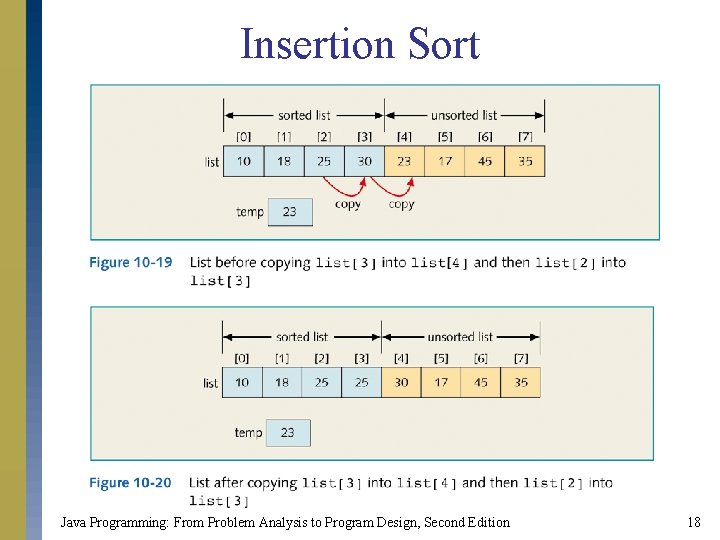
Insertion Sort Java Programming: From Problem Analysis to Program Design, Second Edition 18

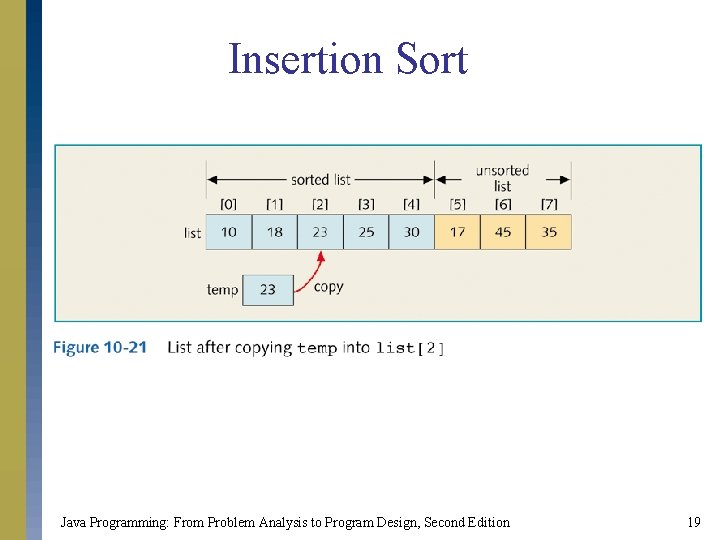
Insertion Sort Java Programming: From Problem Analysis to Program Design, Second Edition 19

Insertion Sort public static void insertion. Sort(int[] list, int no. Of. Elements) { int first. Out. Of. Order, location; int temp; for (first. Out. Of. Order = 1; first. Out. Of. Order < no. Of. Elements; first. Out. Of. Order++) if (list[first. Out. Of. Order] < list[first. Out. Of. Order - 1]) { temp = list[first. Out. Of. Order]; location = first. Out. Of. Order; do { list[location] = list[location - 1]; location--; } while(location > 0 && list[location - 1] > temp); list[location] = temp; } } //end insertion. Sort Java Programming: From Problem Analysis to Program Design, Second Edition 20

Insertion Sort s For a list of length n, on average, the insertion sort makes (n 2 + 3 n – 4) / 4 key comparisons and about n(n – 1) / 4 item assignments. s Therefore, if n = 1000, the insertion sort makes about 250, 000 key comparisons and about 250, 000 item assignments to sort the list. Java Programming: From Problem Analysis to Program Design, Second Edition 21

Sequential Ordered Search public static int seq. Ordered. Search(int[] list, int list. Length, int search. Item) { int loc; boolean found = false; for (loc = 0; loc < list. Length; loc++) if (list[loc] >= search. Item) { found = true; break; } if (found) if (list[loc] == search. Item) return loc; else return -1; //Line 1 2 3 4 //Line 5 //Line 6 //Line //Line 7 8 9 10 11 12 13 } Java Programming: From Problem Analysis to Program Design, Second Edition 22

Binary Search s Can only be performed on a sorted list. s Uses divide and conquer technique to search list. s If L is a sorted list of size n, to determine whether an element is in L, the binary search makes at most 2 * log 2 n + 2 key comparisons. s (Faster than a sequential search. ) Java Programming: From Problem Analysis to Program Design, Second Edition 23

Binary Search Algorithm s Search item is compared with middle element of list. s If search item < middle element of list, search is restricted to first half of the list. s If search item > middle element of list, search is restricted to second half of the list. s If search item = middle element, search is complete. Java Programming: From Problem Analysis to Program Design, Second Edition 24

Binary Search Algorithm Determine whether 75 is in the list. Java Programming: From Problem Analysis to Program Design, Second Edition 25

Binary Search Algorithm public static int binary. Search(int[] list, int list. Length, int search. Item) { int first = 0; int last = list. Length - 1; int mid; boolean found = false; while (first <= last && !found) { mid = (first + last) / 2; if (list[mid] == search. Item) found = true; else if (list[mid] > search. Item) last = mid - 1; else first = mid + 1; } if (found) return mid; else return – 1; } //end binary. Search Java Programming: From Problem Analysis to Program Design, Second Edition 26

Vectors s The class Vector can be used to implement a list. s Unlike an array, the size of a Vector object can grow/shrink during program execution. s You do not need to worry about the number of data elements in a vector. Java Programming: From Problem Analysis to Program Design, Second Edition 27

Members of the class Vector Java Programming: From Problem Analysis to Program Design, Second Edition 28

Members of the class Vector Java Programming: From Problem Analysis to Program Design, Second Edition 29

Members of the class Vector Java Programming: From Problem Analysis to Program Design, Second Edition 30

Members of the class Vector Java Programming: From Problem Analysis to Program Design, Second Edition 31

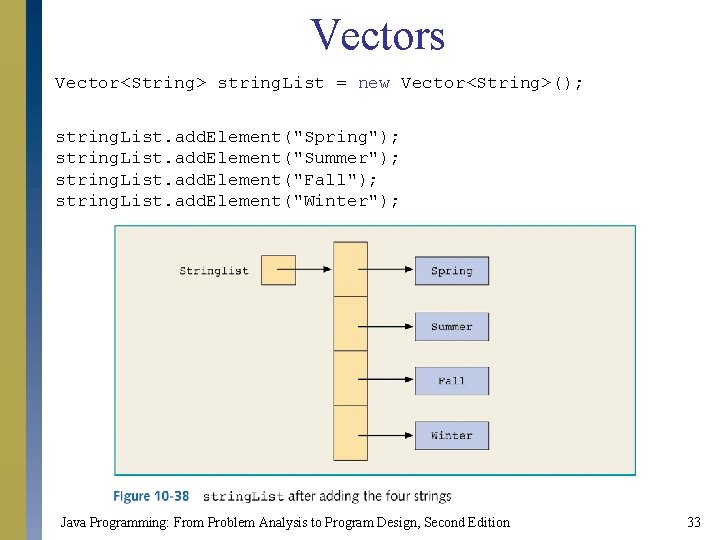
Vectors s Every element of a Vector object is a reference variable of the type Object. s To add an element into a Vector object: s Create appropriate object. s Store data into object. s Store address of object holding data into Vector object element. Java Programming: From Problem Analysis to Program Design, Second Edition 32

Vectors Vector<String> string. List = new Vector<String>(); string. List. add. Element("Spring"); string. List. add. Element("Summer"); string. List. add. Element("Fall"); string. List. add. Element("Winter"); Java Programming: From Problem Analysis to Program Design, Second Edition 33

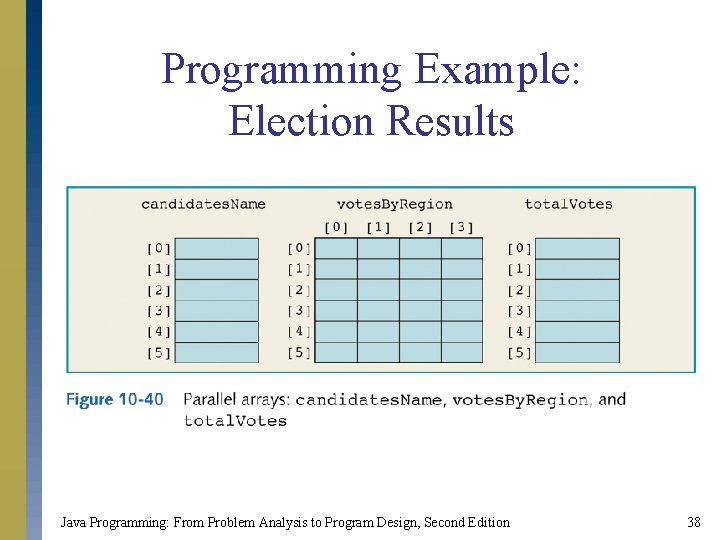
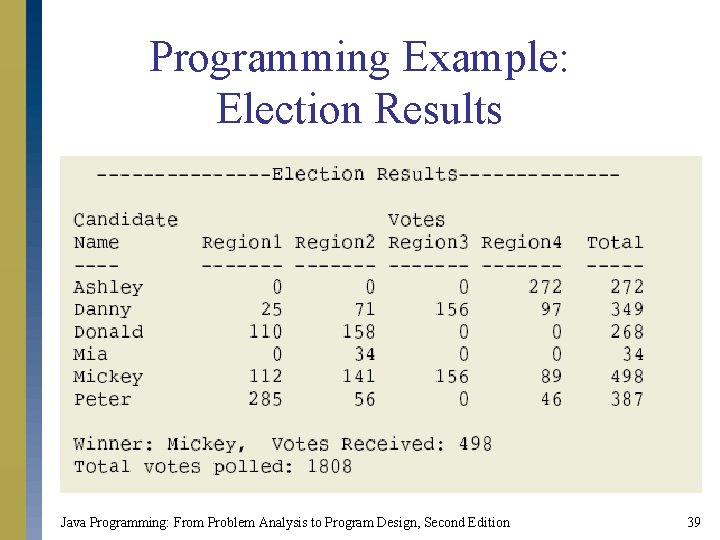
Programming Example: Election Results s Input: Two files s File 1: Candidates’ names s File 2: Voting data s Voting data format: s candidate_name region# number_of_votes_for_this_candidate Java Programming: From Problem Analysis to Program Design, Second Edition 34

Programming Example: Election Results s Output: Election results in a tabular form. s Each candidate’s name. s Number of votes each candidate received in each region. s Total number of votes each candidate received. Java Programming: From Problem Analysis to Program Design, Second Edition 35

Programming Example: Election Results (Solution) The solution includes: s Reading the candidates’ names into the array candidate. Name. s A two-dimensional array consisting of the votes by region. s An array consisting of the total votes parallel to the candidate. Name array. Java Programming: From Problem Analysis to Program Design, Second Edition 36

Programming Example: Election Results (Solution) s s Sorting the array candidates. Name. Processing the voting data. Calculating the total votes received by each candidate. Outputting the results in tabular form. Java Programming: From Problem Analysis to Program Design, Second Edition 37

Programming Example: Election Results Java Programming: From Problem Analysis to Program Design, Second Edition 38

Programming Example: Election Results Java Programming: From Problem Analysis to Program Design, Second Edition 39

Additional String Methods Java Programming: From Problem Analysis to Program Design, Second Edition 40

Additional String Methods Java Programming: From Problem Analysis to Program Design, Second Edition 41

Additional String Methods Java Programming: From Problem Analysis to Program Design, Second Edition 42

Additional String Methods Java Programming: From Problem Analysis to Program Design, Second Edition 43

Effects of Some String Methods Java Programming: From Problem Analysis to Program Design, Second Edition 44

Programming Example: Pig Latin Strings s If string begins with a vowel, “-way” is appended to it. s If first character is not a vowel: s Add “-” to end. s Rotate characters until the first character is a vowel. s Append “ay. ” s Input: String s Output: String in pig Latin Java Programming: From Problem Analysis to Program Design, Second Edition 45

Programming Example: Pig Latin Strings (Solution) s Methods: is. Vowel, rotate, pig. Latin. String s Use methods to: s Get the string (str). s Find the pig Latin form of str by using the method pig. Latin. String. s Output the pig Latin form of str. Java Programming: From Problem Analysis to Program Design, Second Edition 46

Programming Example: Pig Latin Strings (Sample Runs) Java Programming: From Problem Analysis to Program Design, Second Edition 47

Chapter Summary s Lists s Searching lists: s Sequential searching on an order list s Binary search s Sorting lists: s Bubble sort s Selection sort s Insertion sort Java Programming: From Problem Analysis to Program Design, Second Edition 48

Chapter Summary s Programming examples s The class Vector s Members of the class Vector s The class String s Additional methods of the class String Java Programming: From Problem Analysis to Program Design, Second Edition 49