Chapter 14 Recursion Java Programming From Problem Analysis

Chapter 14: Recursion Java Programming: From Problem Analysis to Program Design, Second Edition

Chapter Objectives s Learn about recursive definitions. s Explore the base case and the general case of a recursive definition. s Learn about recursive algorithms. s Learn about recursive methods. s Become aware of direct and indirect recursion. s Explore how to use recursive methods to implement recursive algorithms. Java Programming: From Problem Analysis to Program Design, Second Edition 2

Introduction s // Program prints an array. public class Print { // print array iteratively public static void print. Iterative( int[] array ) { for (int i=0; i< array. length; ++i ) System. out. print(array[i] + " "); // add ending newline } // end method print. Array Java Programming: From Problem Analysis to Program Design, Second Edition 3

s // recursively print array private static void print. Array. Helper( int[] array, int start. Index ) { if ( start. Index == array. length ) return; // print elements in normal order System. out. print( array[ start. Index ] + " " ); print. Array. Helper( array, start. Index + 1 ); } // end method print. Array. Helper Java Programming: From Problem Analysis to Program Design, Second Edition 4

s // recursively print array in reverse order private static void print. Array. Reverse. Helper( int[] array, int start. Index ) { if ( start. Index == array. length ) return; // print elements in reverse order print. Array. Reverse. Helper( array, start. Index + 1 ); System. out. print( array[ start. Index ] + " " ); } // end method print. Array. Helper Java Programming: From Problem Analysis to Program Design, Second Edition 5

s public static void main( String args[] ) { int array[] = { 8, 22, 88, 34, 84, 21, 94 }; System. out. print( "Array is: " ); print. Array. Helper( array, 0 ); // print array System. out. print( "Array in reverse order is: " ); print. Array. Reverse. Helper( array , 0 ); // print array in reverse order } Java Programming: From Problem Analysis to Program Design, Second Edition 6

Recursive Definitions s Recursion: s Process of solving a problem by reducing it to smaller versions of itself. Factorial of an integer: 0! = 1 (14 -1) n! = n X (n-1)! If n > 0 (14 -2) Java Programming: From Problem Analysis to Program Design, Second Edition 7

Recursive Definitions s Recursive definition: s Definition in which a problem is expressed in terms of a smaller version of itself. s Has one or more base cases. Java Programming: From Problem Analysis to Program Design, Second Edition 8

Recursive Definitions s Recursive algorithm: s Algorithm that finds the solution to a given problem by reducing the problem to smaller versions of itself. s Has one or more base cases. s Implemented using recursive methods. s Recursive method: s Method that calls itself. s Base case: s Case in recursive definition in which the solution is obtained directly. s Stops the recursion. Java Programming: From Problem Analysis to Program Design, Second Edition 9

Recursive Factorial Method public static int fact (int num) { if (num == 0) return 1; else return num * fact(num-1); } Java Programming: From Problem Analysis to Program Design, Second Edition 10

Recursive Factorial Method Java Programming: From Problem Analysis to Program Design, Second Edition 11

Recursive Definitions s General solution: s Breaks problem into smaller versions of itself. s General case: s Case in recursive definition in which a smaller version of itself is called. s Must eventually be reduced to a base case. Java Programming: From Problem Analysis to Program Design, Second Edition 12

Tracing a Recursive Method Recursive method: s Has unlimited copies of itself. s Every recursive call has its own: s Code s Set of parameters s Set of local variables Java Programming: From Problem Analysis to Program Design, Second Edition 13

Tracing a Recursive Method s After completing a recursive call: s Control goes back to the calling environment. s Recursive call must execute completely before control goes back to previous call. s Execution in previous call begins from point immediately following recursive call. Java Programming: From Problem Analysis to Program Design, Second Edition 14

Recursive Definitions s Directly recursive: A method that calls itself. s Indirectly recursive: A method that calls another method and eventually results in the original method call. (method A calls method B and method B calls method A) Java Programming: From Problem Analysis to Program Design, Second Edition 15

Recursive Definitions s Tail recursive method: Recursive method in which the last statement executed is the recursive call. s Infinite recursion: The case where every recursive call results in another recursive call. The method will excute until the system runs out of memory Java Programming: From Problem Analysis to Program Design, Second Edition 16

Designing Recursive Methods s Understand problem requirements. s Determine limiting conditions. ( ex: the number of elements in a list) s Identify base cases. Java Programming: From Problem Analysis to Program Design, Second Edition 17

Designing Recursive Methods s Provide direct solution to each base case. s Identify general cases. s Provide solutions to general cases in terms of smaller versions of general cases. Java Programming: From Problem Analysis to Program Design, Second Edition 18

Largest Value in Array public static int largest(int[] list, int lower. Index, int upper. Index) { int max; if (lower. Index == upper. Index) return list[lower. Index]; else { max = largest(list, lower. Index + 1, upper. Index); if (list[lower. Index] >= max) return list[lower. Index]; else return max; } } Java Programming: From Problem Analysis to Program Design, Second Edition 19

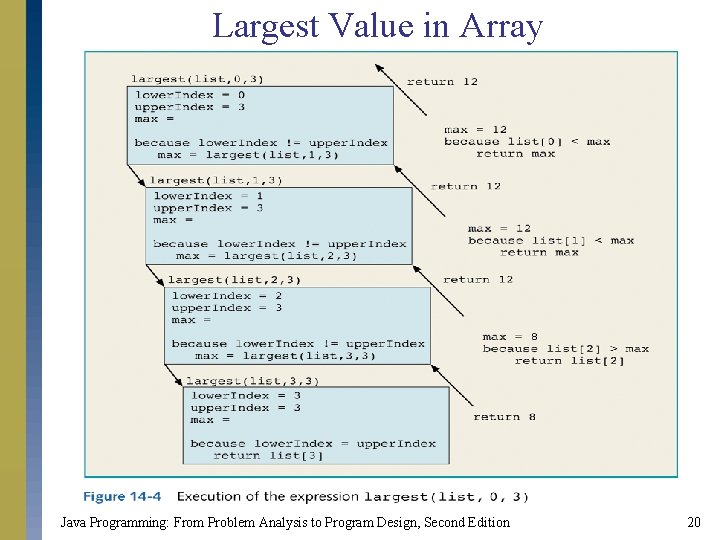
Largest Value in Array Java Programming: From Problem Analysis to Program Design, Second Edition 20

Recursive Fibonacci Java Programming: From Problem Analysis to Program Design, Second Edition 21

Recursive Fibonacci public static int r. Fib. Num(int a, int b, int n) { if(n = = 1) return a; else if (n = = 2) return b; else return r. Fib. Num(a, b, n -1) + r. Fib. Num(a, b, n - 2); } Java Programming: From Problem Analysis to Program Design, Second Edition 22

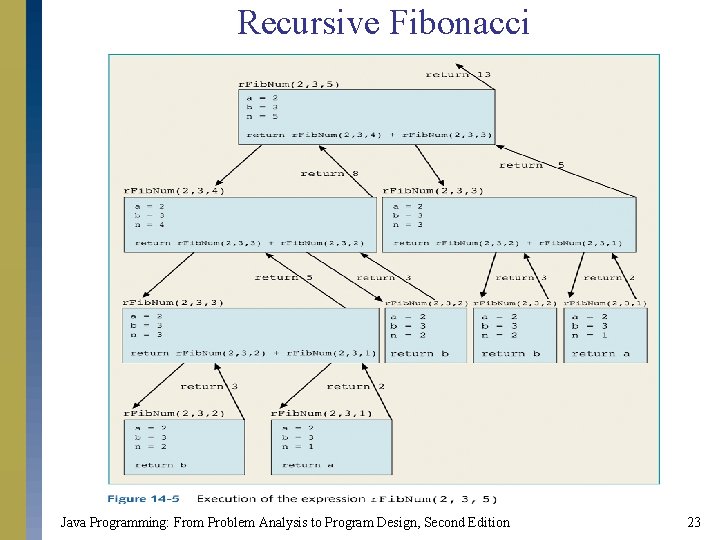
Recursive Fibonacci Java Programming: From Problem Analysis to Program Design, Second Edition 23

Recursion or Iteration? s Two ways to solve particular problem: s Iteration s Recursion s Iterative control structures use looping to repeat a set of statements. s Tradeoffs between two options: s Sometimes recursive solution is easier. s Recursive solution is often slower. Java Programming: From Problem Analysis to Program Design, Second Edition 24

Programming Example: Decimal to Binary Call the remainder of x after division by 2 the right most bit of x. Lets find the binary rep. of 35: Divide 35 by 2. the result is 17 The right most bit of 35 is 1 Divide 17 by 2 = 8 The right most bit of 17 is 1 Divide 8 by 2 = 4 The right most bit of 8 is 0. . Until the quotient = 0 Java Programming: From Problem Analysis to Program Design, Second Edition 25

Programming Example: Decimal to Binary The right most bit of 35 cannot be printed until we have printed the right most bit of 17. The right most bit of 17 cannot be printed until we have printed the right most bit of 8, and so on. The binary rep. of 35 = the binary rep. of 17 follwed by the right most bit of 35 The algorithm: binary (num) = num if num = 0 binary (num) = binary(num / 2) followed by num%2 if num > 0 Java Programming: From Problem Analysis to Program Design, Second Edition 26

Programming Example: Decimal to Binary public static void dec. To. Bin(int num, int base) { if (num > 0) { dec. To. Bin(num / base, base); System. out. print(num % base); } } Java Programming: From Problem Analysis to Program Design, Second Edition 27

Programming Example: Decimal to Binary Java Programming: From Problem Analysis to Program Design, Second Edition 28

Enumeration Types s Java allows programmers to create their own data types by specifying the values of that data type. s These are called enumeration or enum types s They are defined using the key word enum Ex: enum Grades {A, B, C, D, F}; s The values of an enum type are called enumeration or enum constants. s The enum constants within an enum type must be unique. Java Programming: From Problem Analysis to Program Design, Second Edition 29

Enumeration Types s Each enum type is a special type of class, and the values belonging to the enum type are (special types of) objects of that class. s Grades is a class s A, B, C, D, and F are public static reference variables to objects of the type Grades. Java Programming: From Problem Analysis to Program Design, Second Edition 30

Enumeration Types s After an enum type is defined you can declare reference variables of that type. s Grades my. Grade; s Because each of the variables A, B, C, D, and F are public static, they can be accessed using the name of the class and the dot operator. my. Grade = Grades. B; System. out. println(“my. Grade: “ + my. Grade); Output: my. Grade: B Java Programming: From Problem Analysis to Program Design, Second Edition 31

Enumeration Types s Ordinal value: a specific value for each enum constant in an enum type. s The ordinal value of the first enum constant is 0, The ordinal value of the second enum constant is 1, and so on. Java Programming: From Problem Analysis to Program Design, Second Edition 32

Enumeration Types There are some methods associated with enum types: s ordinal() : returns the ordinal value of an enum constant s name(): returns the name of the enum value s values(): returns the values of an enum type as a list Java Programming: From Problem Analysis to Program Design, Second Edition 33

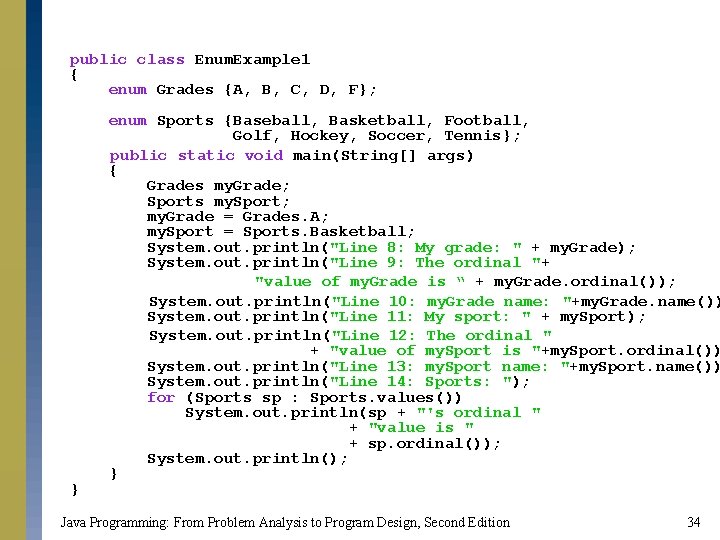
public class Enum. Example 1 { enum Grades {A, B, C, D, F}; } enum Sports {Baseball, Basketball, Football, Golf, Hockey, Soccer, Tennis}; public static void main(String[] args) { Grades my. Grade; Sports my. Sport; my. Grade = Grades. A; my. Sport = Sports. Basketball; System. out. println("Line 8: My grade: " + my. Grade); System. out. println("Line 9: The ordinal "+ "value of my. Grade is “ + my. Grade. ordinal()); System. out. println("Line 10: my. Grade name: "+my. Grade. name()) System. out. println("Line 11: My sport: " + my. Sport); System. out. println("Line 12: The ordinal " + "value of my. Sport is "+my. Sport. ordinal()) System. out. println("Line 13: my. Sport name: "+my. Sport. name()) System. out. println("Line 14: Sports: "); for (Sports sp : Sports. values()) System. out. println(sp + "'s ordinal " + "value is " + sp. ordinal()); System. out. println(); } Java Programming: From Problem Analysis to Program Design, Second Edition 34

output Line 8: My grade: A Line 9: The ordinal value of my. Grade is 0 Line 10: my. Grade name: A Line 11: My sport: Basketball Line 12: The ordinal value of my. Sport is 1 Line 13: my. Sport name: Basketball Line 14: Sports: Baseball's ordinal value is 0 Basketball's ordinal value is 1 Football's ordinal value is 2 Golf's ordinal value is 3 Hockey's ordinal value is 4 Soccer's ordinal value is 5 Tennis's ordinal value is 6 Java Programming: From Problem Analysis to Program Design, Second Edition 35

Enumeration Types enum types can also contain constructors, (private) data members, and methods. 1. Use the word enum rather than class. 2. enum types are implicitly final because enum constants should not be modefied. 3. enum constants are implicitly static. 4. You can declare reference variables of enum type, but you cannot instantiate objects using he operator new. (the constructors of an enum type are implicitly private) Java Programming: From Problem Analysis to Program Design, Second Edition 36

Redefining the enum type Grades public enum Grades { A ("Range 90% to 100%"), B ("Range 80% to 89. 99%"), C ("Range 70% to 79. 99%"), D ("Range 60% to 69. 99%"), F ("Range 0% to 59. 99%"); private final String range; private Grades() // or Grades() without the word private { } range = ""; private Grades(String str) // or Grades(String str) { range = str; } } public String get. Range() { return range; } Java Programming: From Problem Analysis to Program Design, Second Edition 37

Example D-3 public class Enum. Example 2 { public static void main(String[] args) { System. out. println("Grade Ranges"); //Line 1 for (Grades gr : Grades. values()) //Line 2 System. out. println(gr + " " + gr. get. Range()); //Line 3 } } System. out. println(); Java Programming: From Problem Analysis to Program Design, Second Edition //Line 4 38

output Grade Ranges A Range 90% to 100% B Range 80% to 89. 99% C Range 70% to 79. 99% D Range 60% to 69. 99% F Range 0% to 59. 99% Java Programming: From Problem Analysis to Program Design, Second Edition 39