Chapter 14 Heat Work Energy Enthalpy 1 The

Chapter 14 Heat, Work, Energy, Enthalpy 1 The Nature of Energy 2 Enthalpy 3 Thermodynamics of Ideal Gases 4 Calorimetry 5 Hess's Law 6 Standard Enthalpies of Formation 7 Present Sources of Energy (skip) 8 New Energy Sources (skip)

James Prescott Joule (1818 -1889) Highlights – English physicist and !!brewer!! – Studied the nature of heat, and discovered its relationship to mechanical work – Challenged the "caloric theory”l that heat cannot be created nor destroyed. – Led to theory of conservation of energy, which led to the development of the first law of thermodynamics – Worked with Lord Kelvin to develop the absolute scale of temperature – Pupil of John Dalton (Atomic Theory) – Joule effect: found the relationship between the flow of current through a resistance and the heat dissipated, now called Joule's law Moments in a Life (Death) – Gravestone is inscribed with the number “ 772. 55” the amount of work, in ft lb, he determined experimentally to be required to raise the temperature of 1 lb of water by 1° Fahrenheit. “ 772. 55”

Thermite Reaction Reactants → Products 2 Al (s) + Fe 2 O 3 (s) → Al 2 O 3 (s) + 2 Fe (s)

Energy • Definition of Energy: Capacity to do work. • The study of energy and its interconversions is called Thermodynamics. • 1 St Law of Thermodynamics: Conservation of energy. – Energy can be converted from one form to another but cannot be created of destroyed. – The energy of the universe is constant. – The energy of a closed system is constant. – Heat and work are interconvertable

Forms of Energy • • • Chemical Energy Potential energy (e. g. , ΔEpotential= mgΔh) Kinetic energy (e. g. , ΔEKinetic= Δ (1/2 mv 2) Electrical Energy Nuclear Energy • Energy transfer – Through heat – Through work

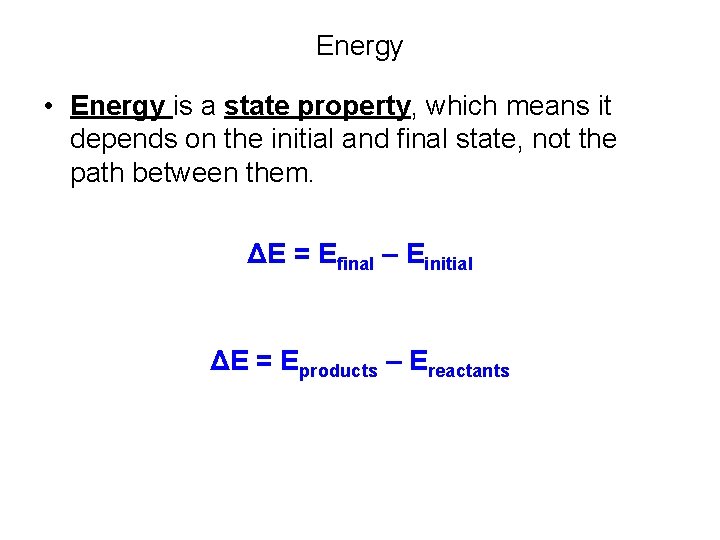
Energy • Energy is a state property, which means it depends on the initial and final state, not the path between them. ΔE = Efinal – Einitial ΔE = Eproducts – Ereactants

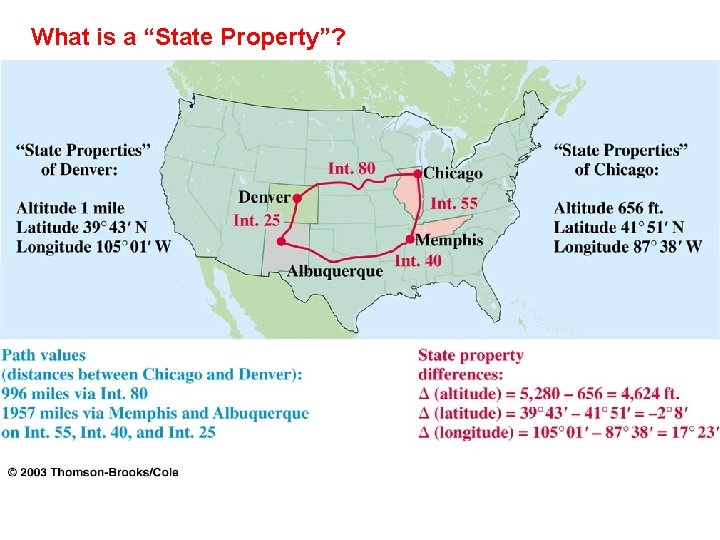
What is a “State Property”?

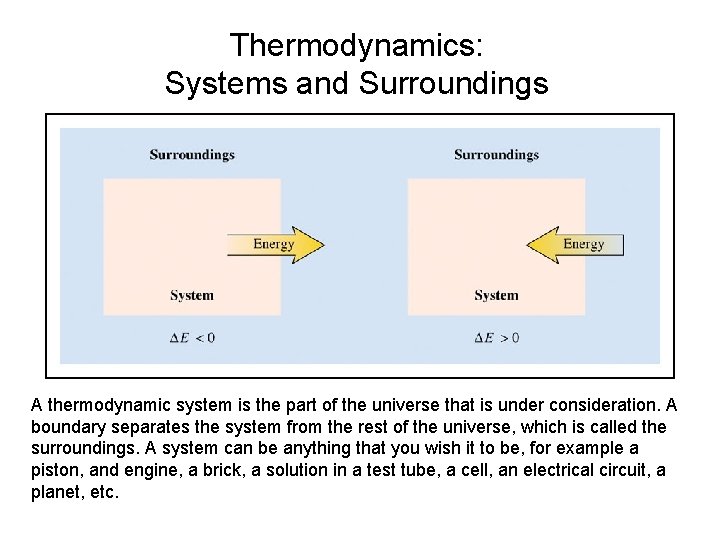
Thermodynamics: Systems and Surroundings A thermodynamic system is the part of the universe that is under consideration. A boundary separates the system from the rest of the universe, which is called the surroundings. A system can be anything that you wish it to be, for example a piston, and engine, a brick, a solution in a test tube, a cell, an electrical circuit, a planet, etc.

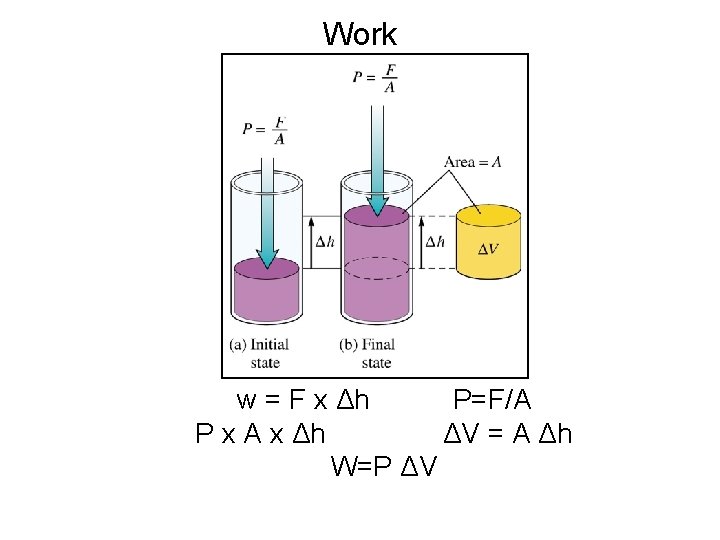
Heat (q) and Work (w) ΔE = q + w • • • q = Heat absorbed by the system ü If q > 0 , heat is absorbed ü If q < 0 , heat is given off w = Work done on the system Increase the energy of a system by heating it (q>0) or by doing work on it (w>0). Work Ø w = Force x distance = (Pressure x area) x distance = pressure x ΔV = PΔV Work is Pressure-Volume work (P-V)

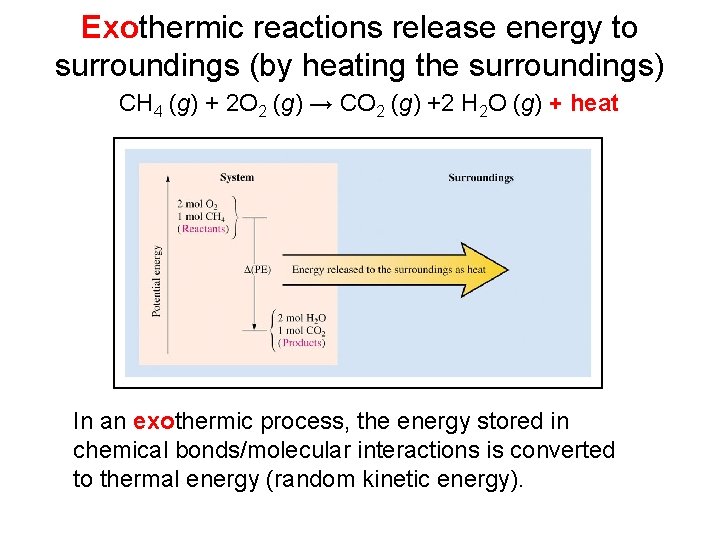
Exothermic reactions release energy to surroundings (by heating the surroundings) CH 4 (g) + 2 O 2 (g) → CO 2 (g) +2 H 2 O (g) + heat In an exothermic process, the energy stored in chemical bonds/molecular interactions is converted to thermal energy (random kinetic energy).

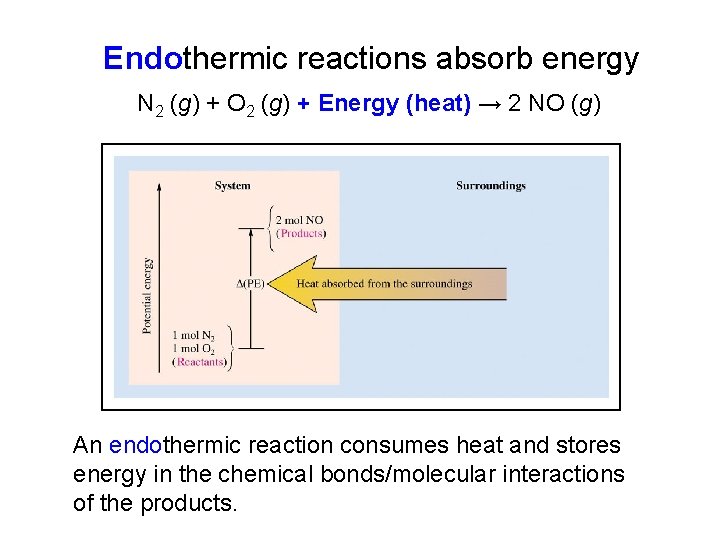
Endothermic reactions absorb energy N 2 (g) + O 2 (g) + Energy (heat) → 2 NO (g) An endothermic reaction consumes heat and stores energy in the chemical bonds/molecular interactions of the products.

Work w = F x Δh P=F/A P x A x Δh ΔV = A Δh W=P ΔV

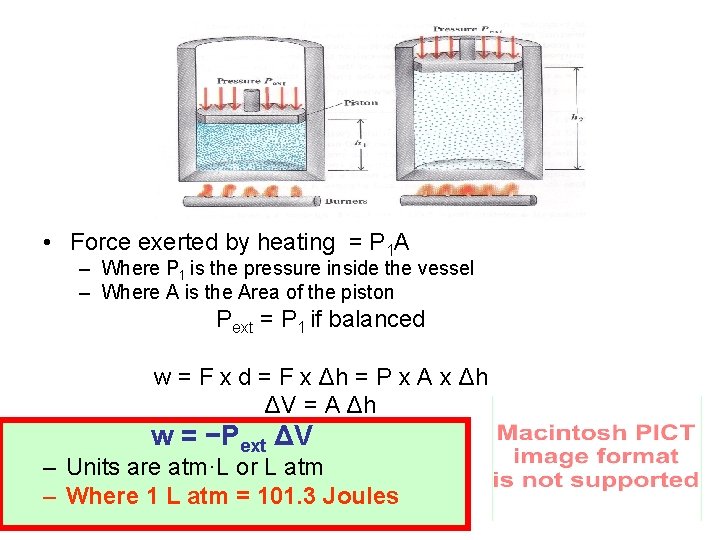
• Force exerted by heating = P 1 A – Where P 1 is the pressure inside the vessel – Where A is the Area of the piston Pext = P 1 if balanced w = F x d = F x Δh = P x A x Δh ΔV = A Δh w = −Pext ΔV – Units are atm·L or L atm – Where 1 L atm = 101. 3 Joules

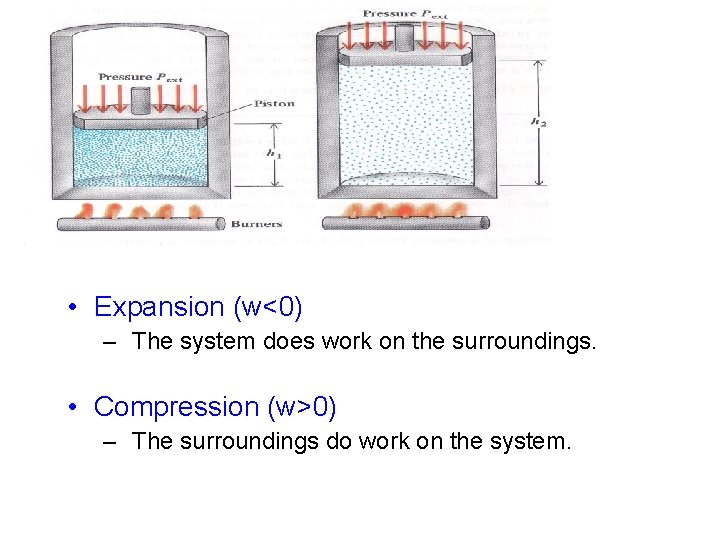
• Expansion (w<0) – The system does work on the surroundings. • Compression (w>0) – The surroundings do work on the system.

Energy • Energy is the capacity to do work. • Energy is a state property, which means it depends on the initial and final state, not the path between them. ΔE = Efinal – Einitial ΔErxn = Eproducts – Ereactants

Enthalpy • Heat is a means by which energy is transferred. • For processes carried out at constant pressure, the heat absorbed equals a change in Enthalpy, ΔH. qp= ΔH Enthalpy Change (p denotes constant pressure) • Enthalpy is a state property, which means it depends on its initial and final state, not the path between them. ΔH = Hfinal – Hinitial ΔHrxn = Hproducts – Hreactants

Enthalpy • ΔE=q+w = ΔH + w (at constant P) • If a chemical reaction occurs in solution with no PV work (no change in V), then w=0 and ΔE = ΔH. • ΔH for a reaction may be either positive (absorbs heat from surroundings) or negative (disperses heat to the surroundings). • For a gas phase reaction, where ΔV is allowed, then ΔE ≠ ΔH.

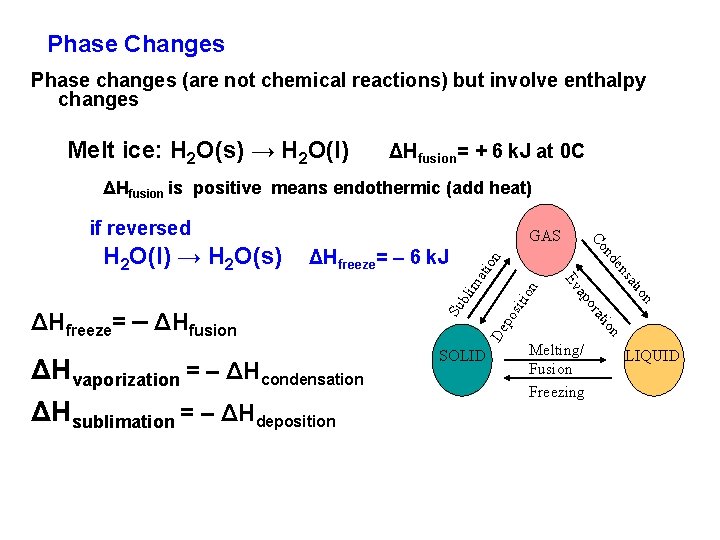
Phase Changes Phase changes (are not chemical reactions) but involve enthalpy changes Melt ice: H 2 O(s) → H 2 O(l) ΔHfusion= + 6 k. J at 0 C ΔHfusion is positive means endothermic (add heat) if reversed on ati sit ion lim De po Su b n tio sa Melting/ Fusion Freezing ion rat po ΔHvaporization = – ΔHcondensation SOLID a Ev ΔHfreeze= – ΔHfusion ΔHsublimation = – ΔHdeposition en ΔHfreeze= – 6 k. J nd Co H 2 O(l) → H 2 O(s) GAS LIQUID

Thermodynamics of Ideal Gases (volume changes) (KE)avg is the average translational energy of 1 mole of a perfect gas. The energy (“heat”) required to change the translational energy of 1 mole of an ideal gas by ΔT is

Heat Capacity (C) • How much heat is required to raise the temp of one mole of something by 1 degree? C is a proportionality constant linking T and q. CΔT=q If no work is allowed (ΔV = 0) CvΔT=q If work is allowed (ΔP=0) CpΔT=q Cp>Cv

Heating an Ideal Gas Molar Heat Capacity (C) of a substance is defined as the heat (q) required to raise the temperature of 1 mole of a substance by 1 K. • Molar Heat Capacity: Cv = 3/2 R (constant volume) (for a perfect monatomic gas) • Molar Heat Capacity: Cp = 5/2 R (constant pressure) (for a perfect monatomic gas) • polyatomic molecules have larger Cv‘s & Cp’s due to vibrational and rotational degrees of freedom.

Thermodynamic Properties of an Ideal Gas ΔE = q + w = ΔH + w (const P) ΔH = ΔE + (PΔV) = qp ΔH = ΔE + PΔV = ΔE + n. RΔT = qp

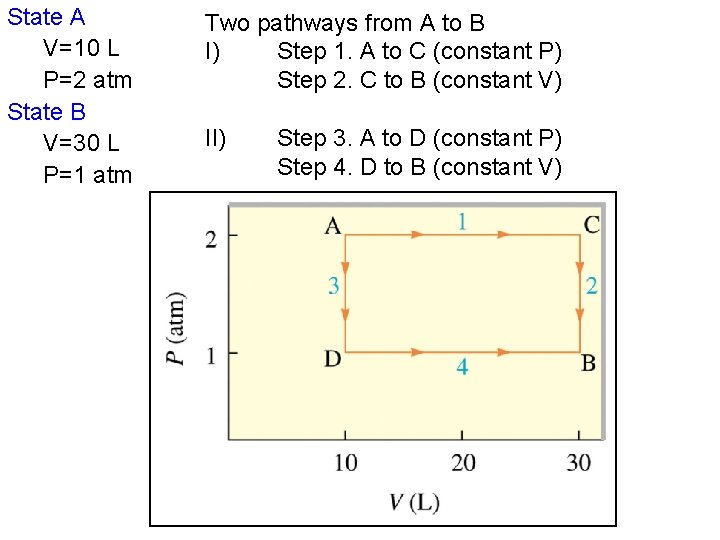
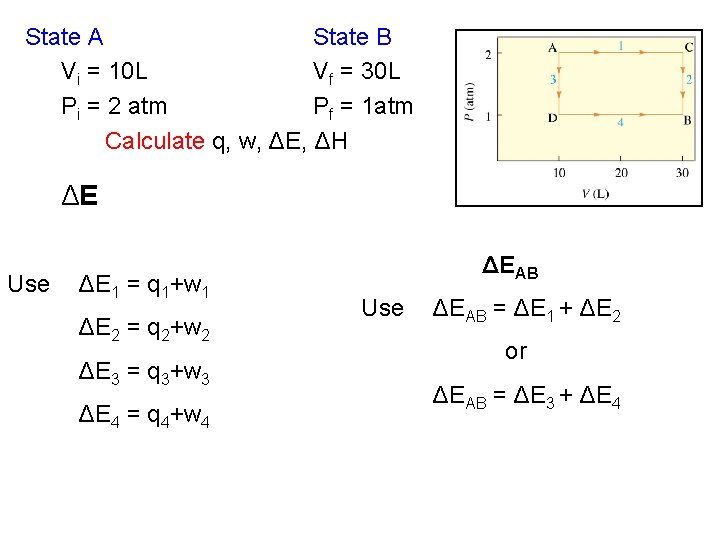
Example Consider 2. 00 mol of a monoatomic ideal gas that is take from state A (PA = 2. 00 atm, VA = 10. 0 L) to state B (PB = 1. 00 atm, VB = 30. 0 L) Calculate q, w, ΔE, and ΔH Know: PV=n. RT, and Cp, Cv, for monatomic gas. Conversion: L-atm to Joules = 1 L atm = 101. 3 Joules

State A V=10 L P=2 atm State B V=30 L P=1 atm Two pathways from A to B I) Step 1. A to C (constant P) Step 2. C to B (constant V) II) Step 3. A to D (constant P) Step 4. D to B (constant V)

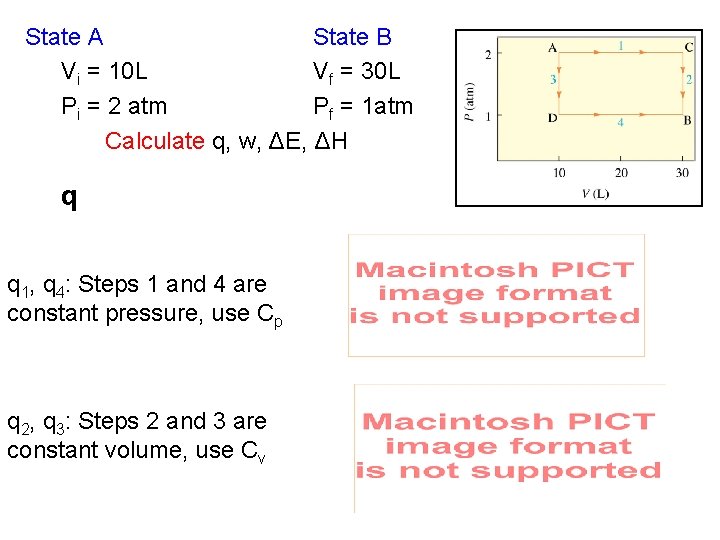
State A State B Vi = 10 L Vf = 30 L Pi = 2 atm Pf = 1 atm Calculate q, w, ΔE, ΔH q q 1, q 4: Steps 1 and 4 are constant pressure, use Cp q 2, q 3: Steps 2 and 3 are constant volume, use Cv

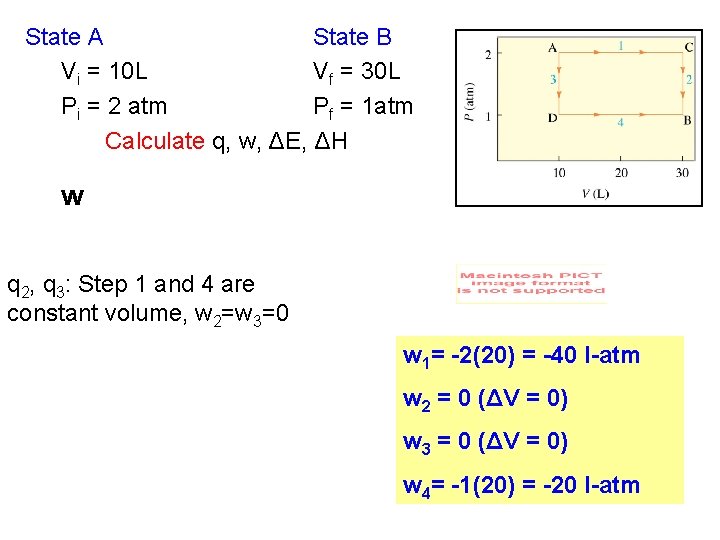
State A State B Vi = 10 L Vf = 30 L Pi = 2 atm Pf = 1 atm Calculate q, w, ΔE, ΔH w q 2, q 3: Step 1 and 4 are constant volume, w 2=w 3=0 w 1= -2(20) = -40 l-atm w 2 = 0 (ΔV = 0) w 3 = 0 (ΔV = 0) w 4= -1(20) = -20 l-atm

State A State B Vi = 10 L Vf = 30 L Pi = 2 atm Pf = 1 atm Calculate q, w, ΔE, ΔH ΔE Use ΔE 1 = q 1+w 1 ΔE 2 = q 2+w 2 ΔE 3 = q 3+w 3 ΔE 4 = q 4+w 4 ΔEAB Use ΔEAB = ΔE 1 + ΔE 2 or ΔEAB = ΔE 3 + ΔE 4

Heat Capacity • Heat Capacity, Cp, is the amount of heat required to raise the temperature of a substance by one degree at constant pressure. ü Cp is always a positive number ü q and ΔT can be both negative or positive Ø If q is negative, then heat is evolved or given off and the temperature decreases Ø If q is positive, then heat is absorbed and the temperature increases

Heat Capacity (continued) • Cp units are energy per temp. change • Cp units are Joule/o. K or JK-1 • Molar heat capacity • Units are J/K/mole or JK-1 mol-1

Specific Heat Capacity • The word Specific before the name of a physical quantity very often means divided by the mass • Specific Heat Capacity is the amount of heat required to raise the temperature of one gram of material by one degree Kelvin (at constant pressure)

Standard State Enthalpies • Designated using a superscript ° (pronounced naught) • Is written as ΔH° • OFB text appendix D lists standard enthalpies of formation of one mole of a variety of chemical species at 1 atm and 25°C. • Standard State conditions – All concentrations are 1 M or 1 mol/L – All partial pressures are 1 atm

Standard Enthalpies of Formation ΔH°rx is the sum of products minus the sum of the reactants For a general reaction a. A+b. B→c. C+d. D

Enthalpy of Reaction: ΔHrxn CO (g) + ½ O 2 (g) → CO 2 (g)

CO (g) + ½ O 2 (g) → CO 2 (g) ΔH°rxn= – 283 k. J/mol An exothermic reaction If stoichiometric coefficients are doubled (x 2), then double ΔH° 2 CO (g) + 1 O 2 (g) → 2 CO 2 (g) ΔH°rxn= (2)(-283 k. J/mol) If the reaction direction is reversed CO 2 (g) → CO (g) + ½ O 2 (g) Change the sign of ΔH°rxn

How much heat at constant pressure is needed to decompose 9. 74 g of HBr (g) (mwt =80. 9 g/mol) into its elements? H 2 + Br 2 → 2 HBr (g) ΔH°rxn = -72. 8 k. Jmol-1 Strategy: • Decomposition is actually the reverse reaction • ΔH to decompose 2 moles of HBr is +72. 8 k. J/mol

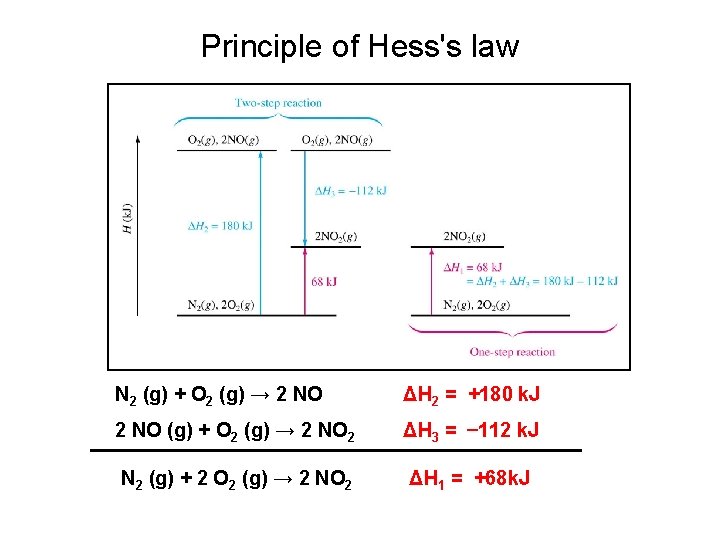
Hess’s Law • Sometimes its difficult or even impossible to conduct some experiments in the lab. • Because Enthalpy (H) is a State Property, it doesn’t matter what path is taken as long as the initial reactants lead to the final product. • Hess’s Law is about adding or subtracting equations and enthalpies. • Hess’s Law: If two or more chemical equations are added to give a new equation, then adding the enthalpies of the reactions that they represent gives the enthalpy of the new reaction.

Principle of Hess's law N 2 (g) + O 2 (g) → 2 NO ΔH 2 = +180 k. J 2 NO (g) + O 2 (g) → 2 NO 2 ΔH 3 = – 112 k. J N 2 (g) + 2 O 2 (g) → 2 NO 2 ΔH 1 = +68 k. J

Suppose hydrazine and oxygen react to give dinitrogen pentaoxide and water vapor: 2 N 2 H 4 (l) + 7 O 2 (g) → 2 N 2 O 5 (s) + 4 H 2 O (g) Calculate the ΔH of this reaction, given that the reaction: N 2 (g) + 5/2 O 2 (g) → N 2 O 5 (s) has a ΔH of -43 k. J.

2 N 2 H 4 (l) + 7 O 2 (g) → 2 N 2 O 5 (s) + 4 H 2 O (g) ΔHr° = 2 x ΔHf°N 2 O 5 (s) + 4 x ΔHf°H 2 O (g) – 2 x ΔHf° N 2 H 4 (l) – 7 x ΔHf°O 2 (g) What values to use? ΔHf°N 2 O 5 (s) given ΔH° = ─ 43 k. Jmol-1 ΔHf°H 2 O (g) look up in App. 4 ΔHf° N 2 H 4 (l) look up in App. 4 ΔHf°O 2 (g) look up in App. 4 = ΔHr° =