Chapter 14 Frequency Response Chapter Objectives Understand the

Chapter 14 Frequency Response Chapter Objectives: Ø Understand the Concept of Transfer Functions. Ø Be Familiar with the Decibel Scale. Ø Learn how to make Bode Magnitude and Phase plots. Ø Learn about series and parallel resonant RLC circuits. Ø Know Different Types of Passive and Active Filters and their Characteristics. Ø Understand the use of scaling in circuit analysis. Ø Be Able to use PSpice to obtain frequency response. Ø Apply what is learnt to radio receiver and touch-tone telephone. Huseyin Bilgekul Eeng 224 Circuit Theory II Department of Electrical and Electronic Engineering Eastern Mediterranean University Eeng 224 1

FREQUENCY RESPONSE What is Frequency Response of a Circuit? It is the variation in a circuit’s behavior with change in signal frequency and may also be considered as the variation of the gain and phase with frequency. Eeng 224 2

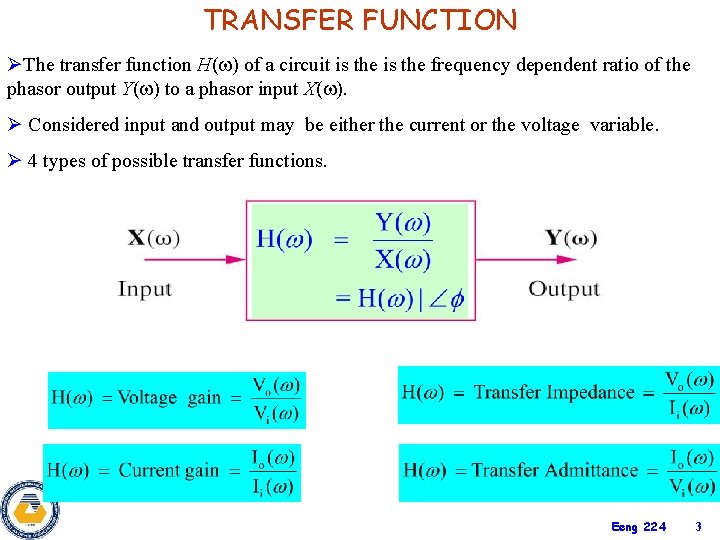
TRANSFER FUNCTION ØThe transfer function H( ) of a circuit is the frequency dependent ratio of the phasor output Y( ) to a phasor input X( ). Ø Considered input and output may be either the current or the voltage variable. Ø 4 types of possible transfer functions. Eeng 224 3

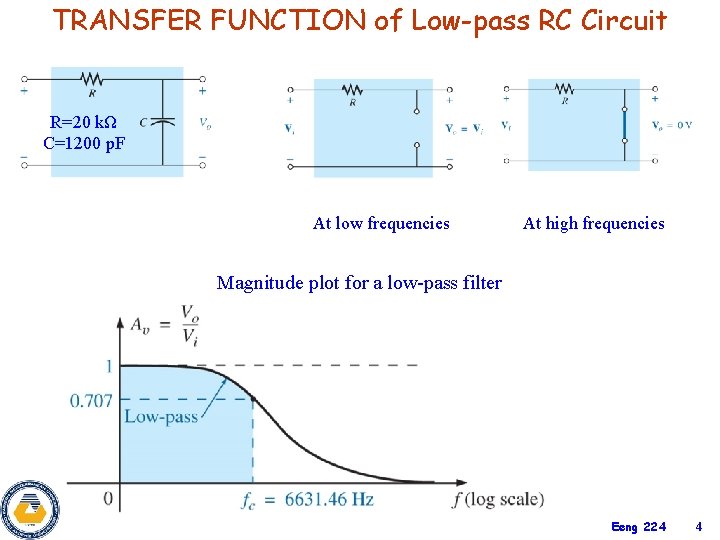
TRANSFER FUNCTION of Low-pass RC Circuit R=20 kΩ C=1200 p. F At low frequencies At high frequencies Magnitude plot for a low-pass filter Eeng 224 4

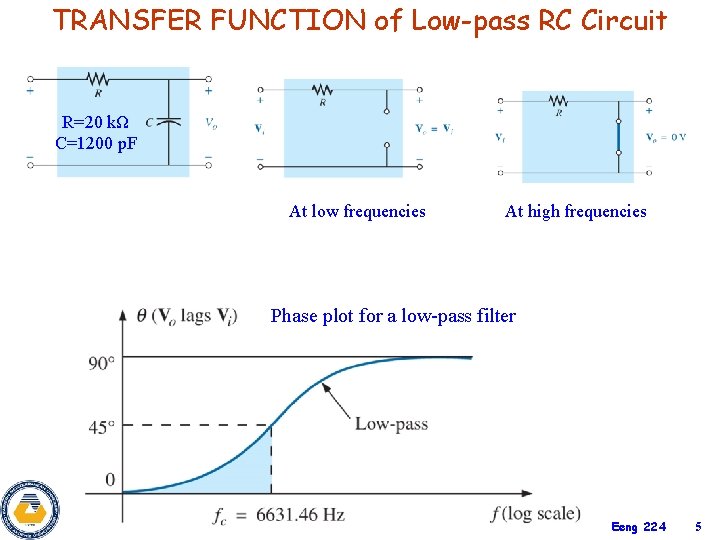
TRANSFER FUNCTION of Low-pass RC Circuit R=20 kΩ C=1200 p. F At low frequencies At high frequencies Phase plot for a low-pass filter Eeng 224 5

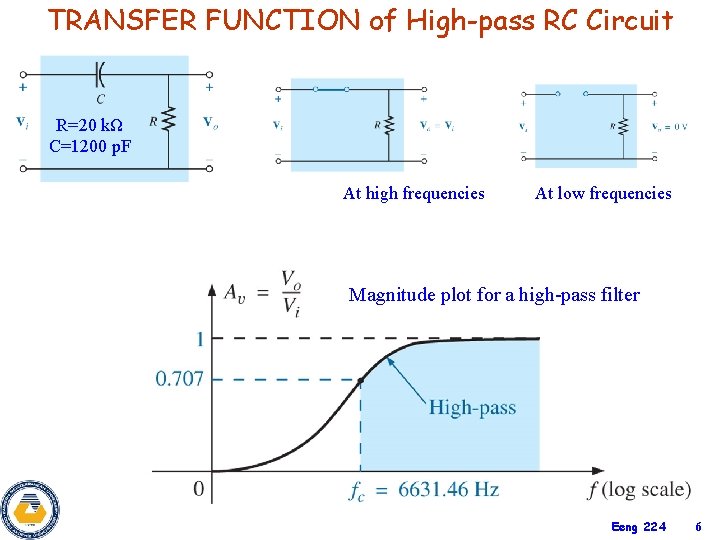
TRANSFER FUNCTION of High-pass RC Circuit R=20 kΩ C=1200 p. F At high frequencies At low frequencies Magnitude plot for a high-pass filter Eeng 224 6

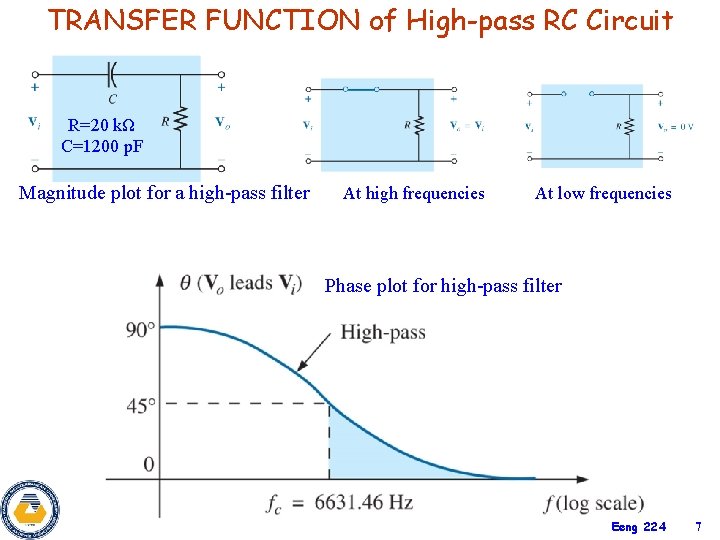
TRANSFER FUNCTION of High-pass RC Circuit R=20 kΩ C=1200 p. F Magnitude plot for a high-pass filter At high frequencies At low frequencies Phase plot for high-pass filter Eeng 224 7

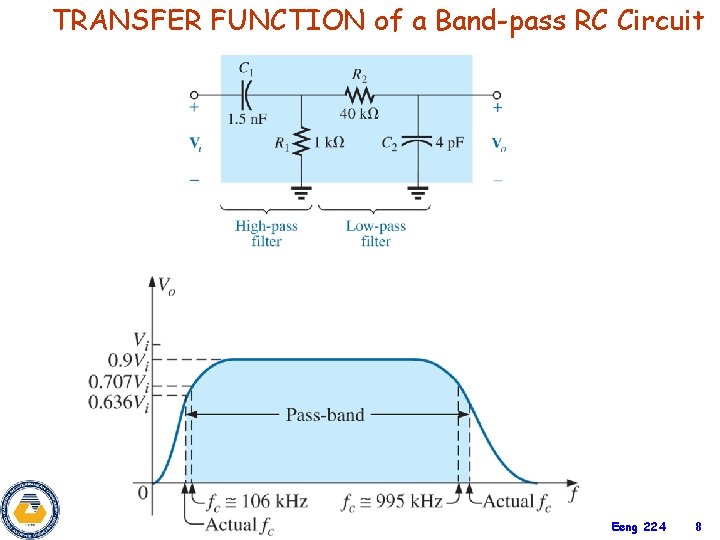
TRANSFER FUNCTION of a Band-pass RC Circuit Eeng 224 8

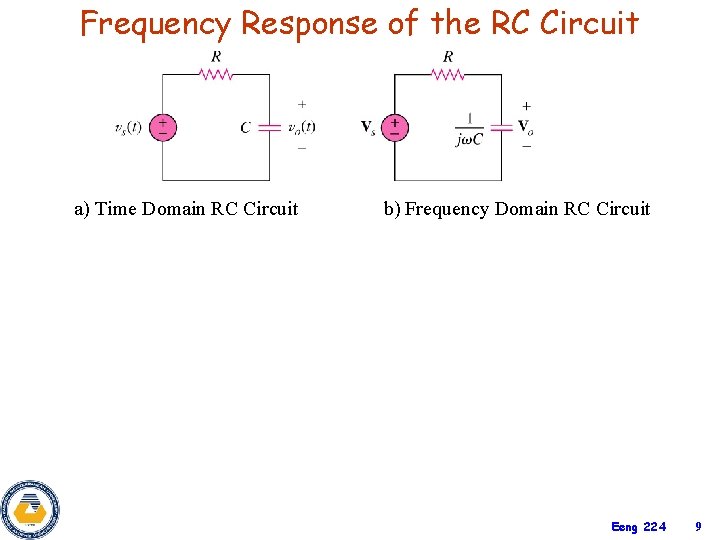
Frequency Response of the RC Circuit a) Time Domain RC Circuit b) Frequency Domain RC Circuit Eeng 224 9

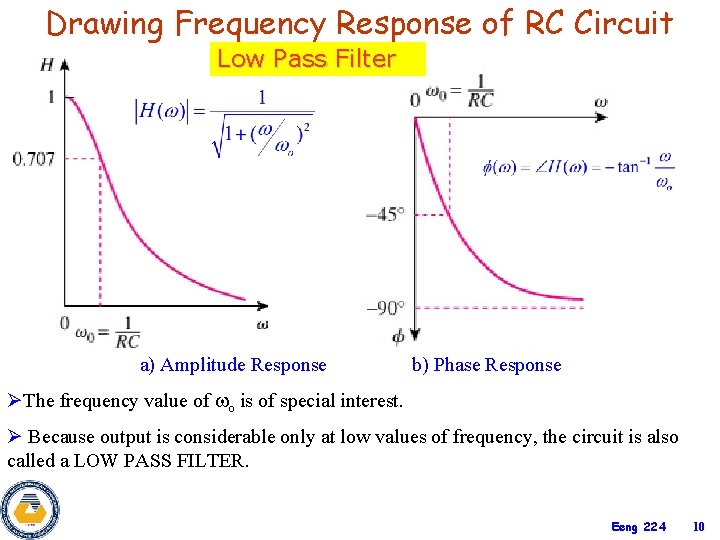
Drawing Frequency Response of RC Circuit Low Pass Filter a) Amplitude Response b) Phase Response ØThe frequency value of o is of special interest. Ø Because output is considerable only at low values of frequency, the circuit is also called a LOW PASS FILTER. Eeng 224 10

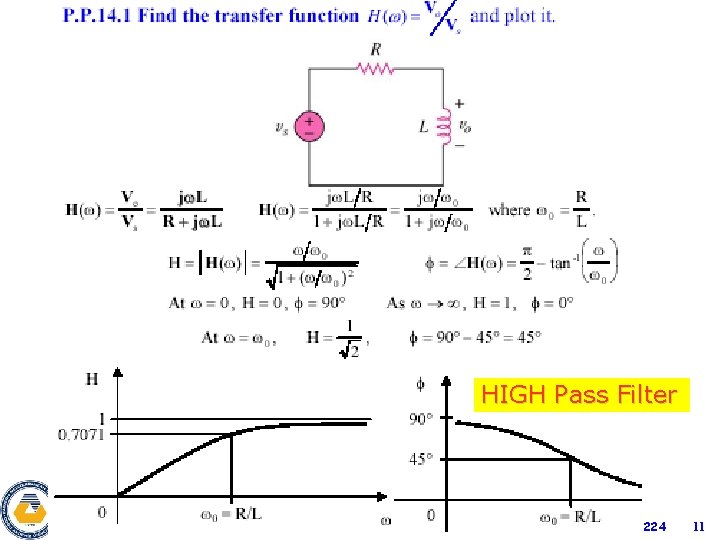
HIGH Pass Filter Eeng 224 11

TRANSFER FUNCTION Ø The transfer function H( ) can be expressed in terms of its numerator polynomial N( ) and its denominator polynomial D( ). Ø The roots of N( )=0 are called ZEROS of H( ) (j =z 1, z 2, z 3, …. ). Similarly The roots of D( )=0 are called POLES of H( ) (j =p 1, p 2, p 3, …. ). A zero as a root of the numerator polynomial, results in a zero value of the transfer function. A pole as a root of the denominator polynomial, results in an infinite value of the transfer function. Eeng 224 12

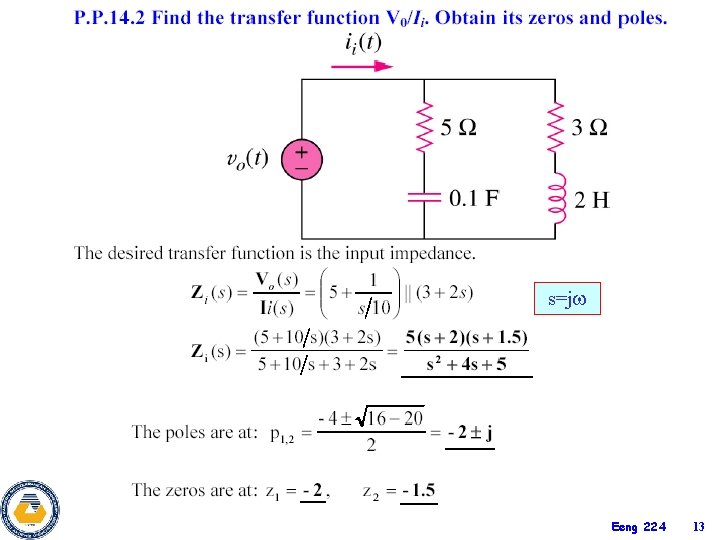
s=j Eeng 224 13

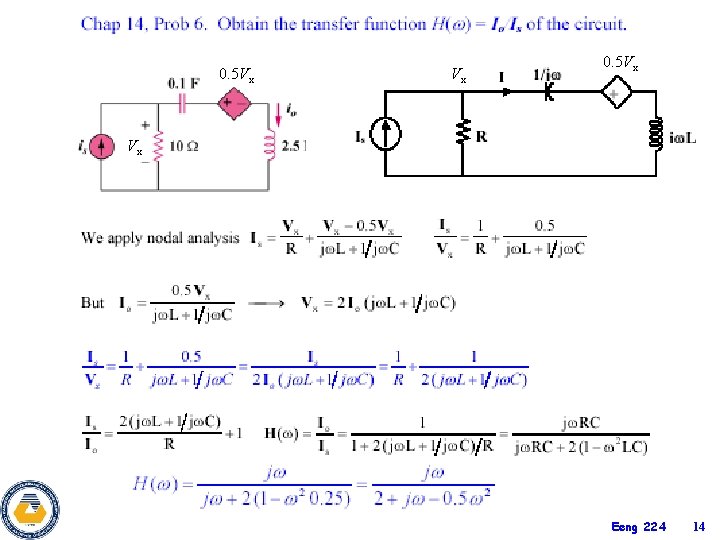
0. 5 Vx Vx Eeng 224 14