Chapter 14 CIRCLES Proof Geometry Definitions A circle

Chapter 14: CIRCLES!!! Proof Geometry

Definitions A circle is the set of all points of a plane that are equidistant from a single point. Picture: A sphere is the set of all points in space that are equidistant from a single point. Picture:

Definitions Circles (or spheres) that share the same center are called concentric. Picture:

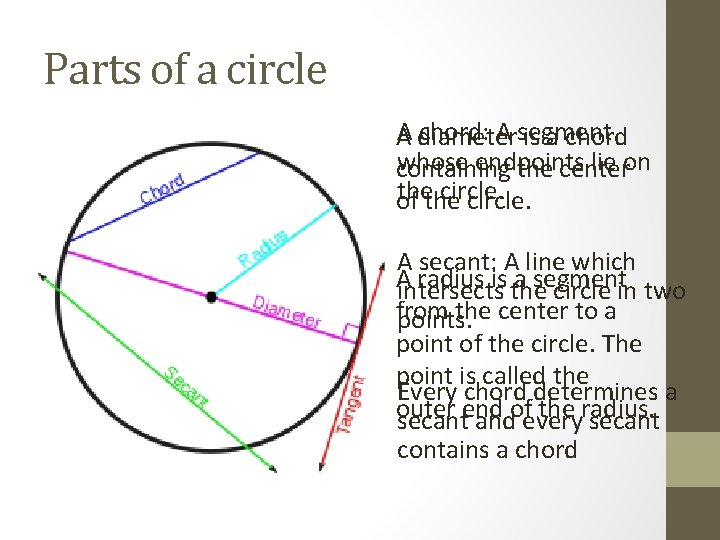
Parts of a circle A diameter chord: A segment is a chord whose endpoints lie on containing the center thethe circle. of circle. A secant: A line which A radius is the a segment intersects circle in two from the center to a points. point of the circle. The point is called the Every chord determines a outer the radius. secantend andofevery secant contains a chord

Recall: What’s a tangent again? A tangent to a circle is a line which intersects the circle in one and only one point. This point is called the point of tangency or the point of contact. We say that the line and the circle are tangent at this point.

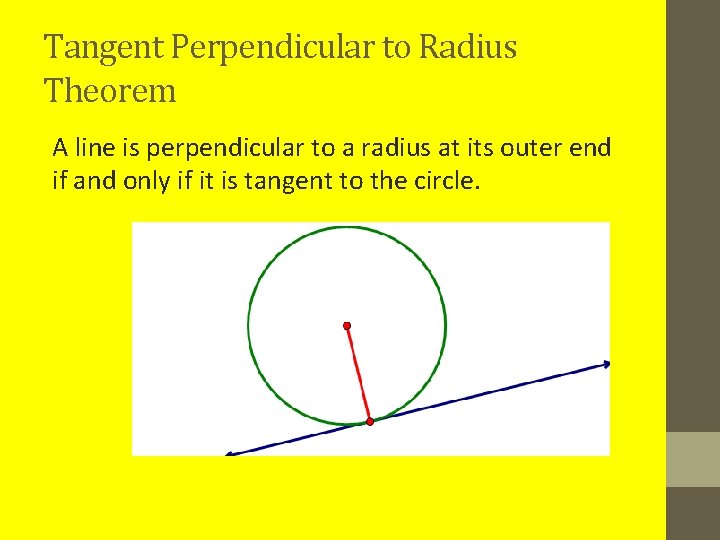
Tangent Perpendicular to Radius Theorem A line is perpendicular to a radius at its outer end if and only if it is tangent to the circle.

Definitions: Interior and Exterior A point is on the interior of a circle if the distance from the center is less than the radius. A point is on the exterior of a circle if the distance from the center is greater than the radius.

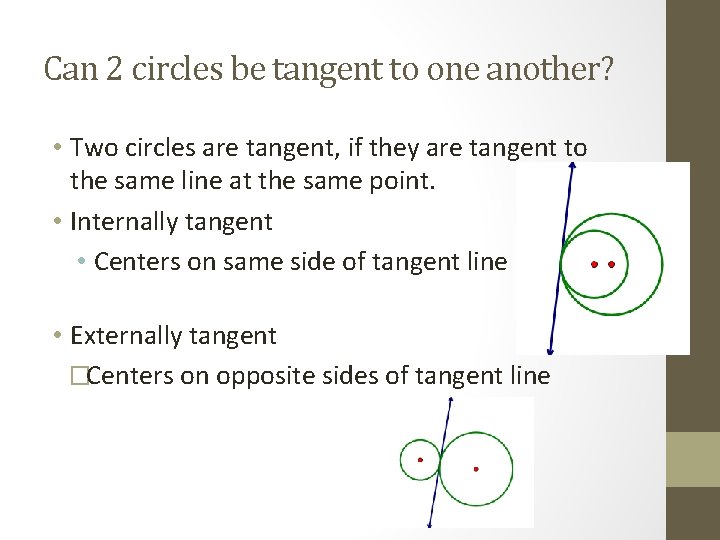
Can 2 circles be tangent to one another? • Two circles are tangent, if they are tangent to the same line at the same point. • Internally tangent • Centers on same side of tangent line • Externally tangent �Centers on opposite sides of tangent line

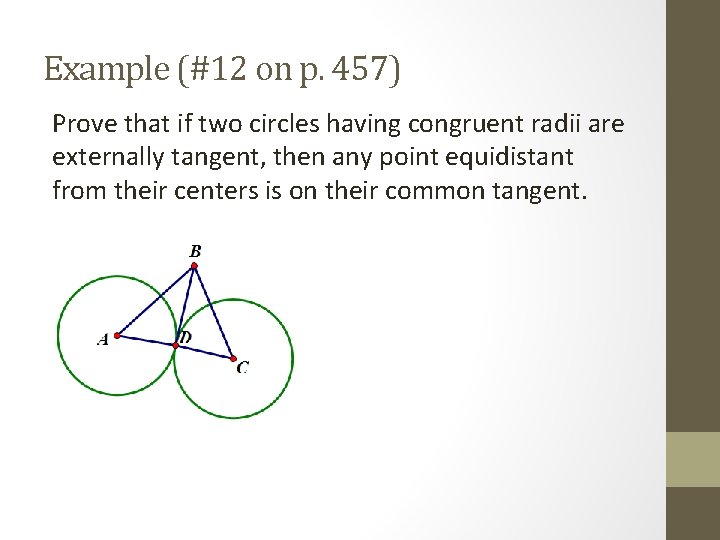
Example (#12 on p. 457) Prove that if two circles having congruent radii are externally tangent, then any point equidistant from their centers is on their common tangent.

Homework pg. 452: # 2, 5 Pg. 456 #4, 5, 9, 11, 13, 14