Chapter 14 Arithmetic Circuits Rev 1 0 05122003

Chapter 14 Arithmetic Circuits Rev. 1. 0 05/12/2003 Rev. 2. 0 06/05/2003 1 EE 141 Arithmetic Circuits

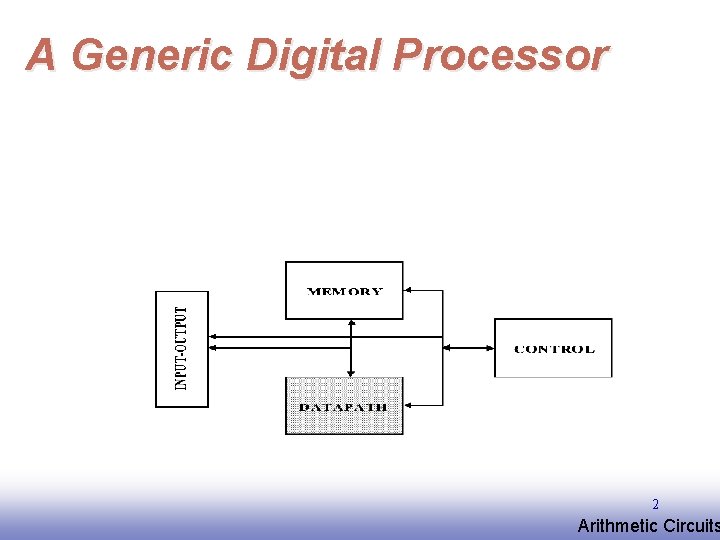
A Generic Digital Processor 2 EE 141 Arithmetic Circuits

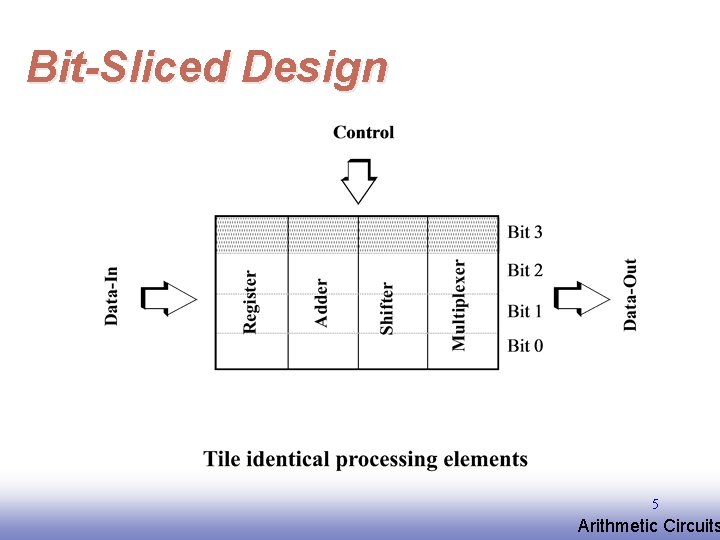
Building Blocks for Digital Architectures Arithmetic and Unit - Bit-sliced datapath (adder, multiplier, shifter, comparator, etc. ) Memory - RAM, ROM, Buffers, Shift registers Control - Finite state machine (PLA, random logic. ) - Counters Interconnect - Switches - Arbiters - Bus 3 EE 141 Arithmetic Circuits

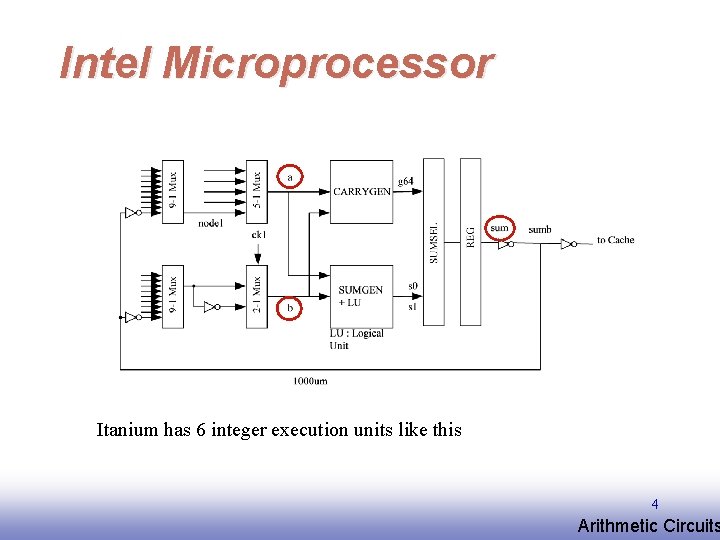
Intel Microprocessor Itanium has 6 integer execution units like this 4 EE 141 Arithmetic Circuits

Bit-Sliced Design 5 EE 141 Arithmetic Circuits

Itanium Integer Datapath EE 141 Fetzer, Orton, ISSCC’ 02 6 Arithmetic Circuits

Adders 7 EE 141 Arithmetic Circuits

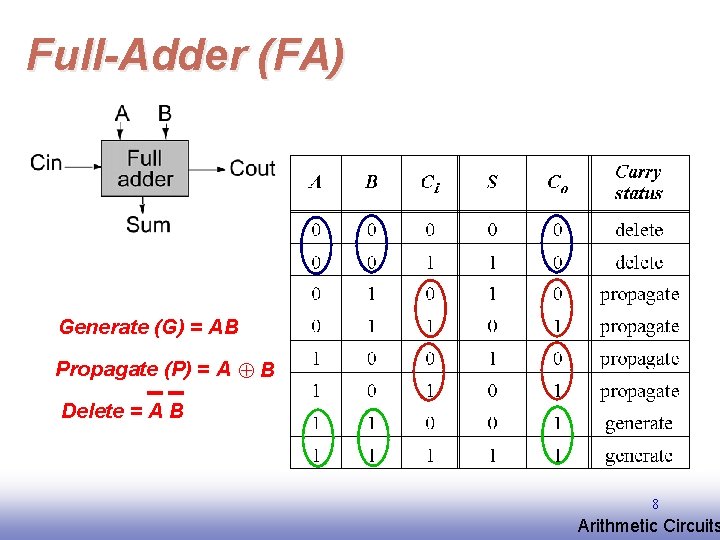
Full-Adder (FA) Generate (G) = AB Propagate (P) = A Å B Delete = A B 8 EE 141 Arithmetic Circuits

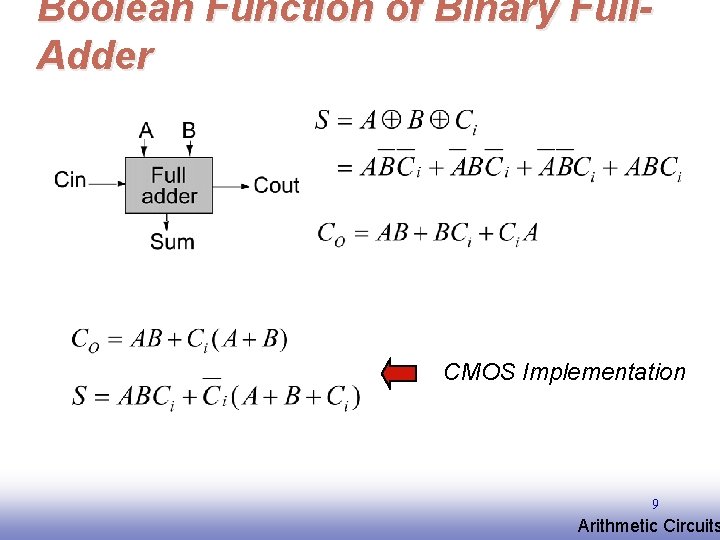
Boolean Function of Binary Full. Adder CMOS Implementation 9 EE 141 Arithmetic Circuits

Express Sum and Carry as a function of P, G, D Define 3 new variable which ONLY depend on A, B Generate (G) = AB Propagate (P) = A Å B Delete = A B Can also derive expressions for S and Co based on D and P Note that we will be sometimes using an alternate definition for Propagate (P) = A + B 10 EE 141 Arithmetic Circuits

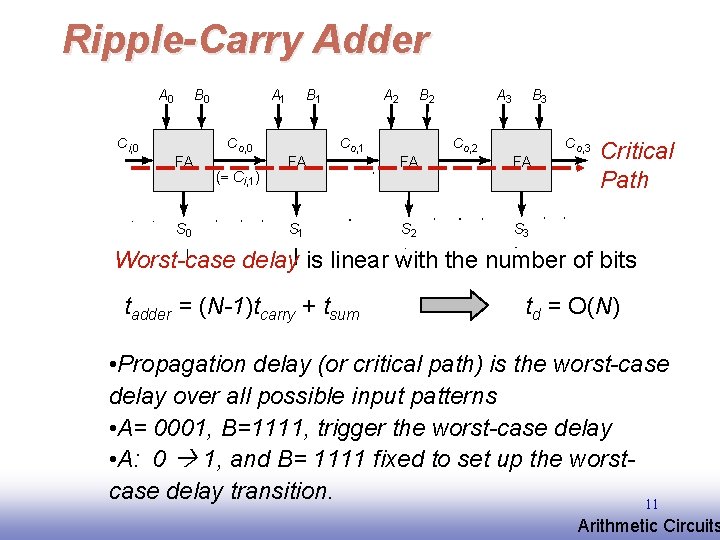
Ripple-Carry Adder A 0 Ci, 0 B 0 FA S 0 A 1 Co, 0 (= Ci, 1) B 1 FA A 2 Co, 1 S 1 B 2 FA S 2 A 3 Co, 2 B 3 FA Co, 3 Critical Path S 3 Worst-case delay is linear with the number of bits tadder = (N-1)tcarry + tsum td = O(N) • Propagation delay (or critical path) is the worst-case delay over all possible input patterns • A= 0001, B=1111, trigger the worst-case delay • A: 0 1, and B= 1111 fixed to set up the worstcase delay transition. 11 EE 141 Arithmetic Circuits

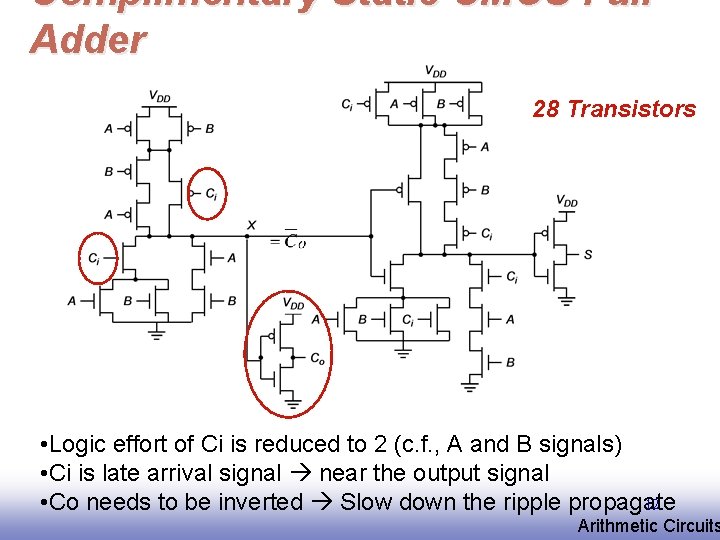
Complimentary Static CMOS Full Adder 28 Transistors • Logic effort of Ci is reduced to 2 (c. f. , A and B signals) • Ci is late arrival signal near the output signal 12 • Co needs to be inverted Slow down the ripple propagate EE 141 Arithmetic Circuits

Inversion Property 13 EE 141 Arithmetic Circuits

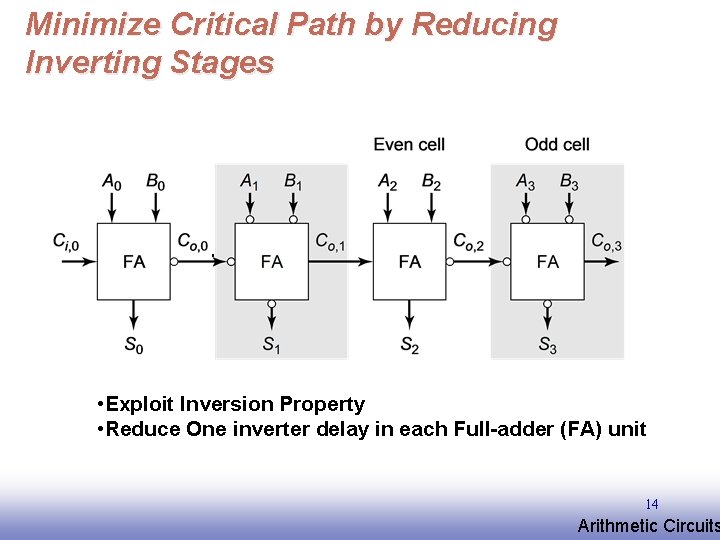
Minimize Critical Path by Reducing Inverting Stages • Exploit Inversion Property • Reduce One inverter delay in each Full-adder (FA) unit 14 EE 141 Arithmetic Circuits

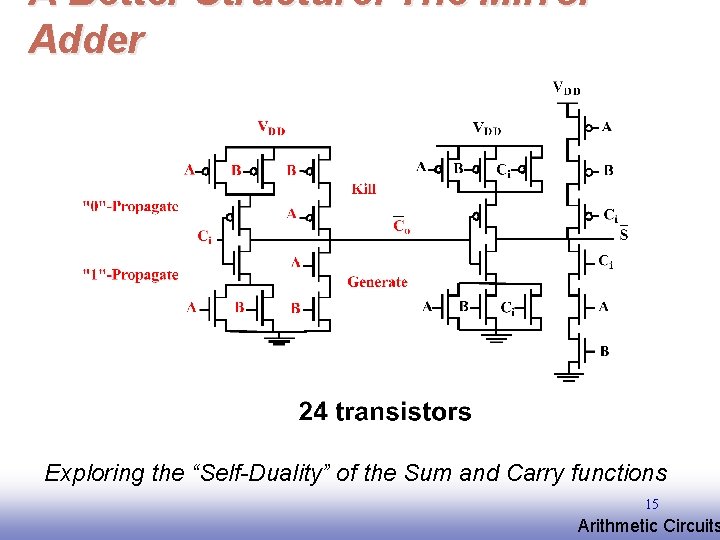
A Better Structure: The Mirror Adder Exploring the “Self-Duality” of the Sum and Carry functions 15 EE 141 Arithmetic Circuits

Mirror Adder: Stick Diagram 16 EE 141 Arithmetic Circuits

Mirror Adder Design • The NMOS and PMOS chains are completely symmetrical • A maximum of two series transistors can be observed in the carry-generation circuitry for good speed. • When laying out the cell, the most critical issue is the minimization of the capacitance at node Co. • The capacitance at node Co is composed of four diffusion capacitances, two internal gate capacitances, and six gate capacitances in the connecting adder cell. • The transistors connected to Ci are placed closest to the output. 17 EE 141 Arithmetic Circuits

Transmission-Gate Full Adder (24 T) • Same delay for Sum and Carry Multiplier design 18 EE 141 Arithmetic Circuits

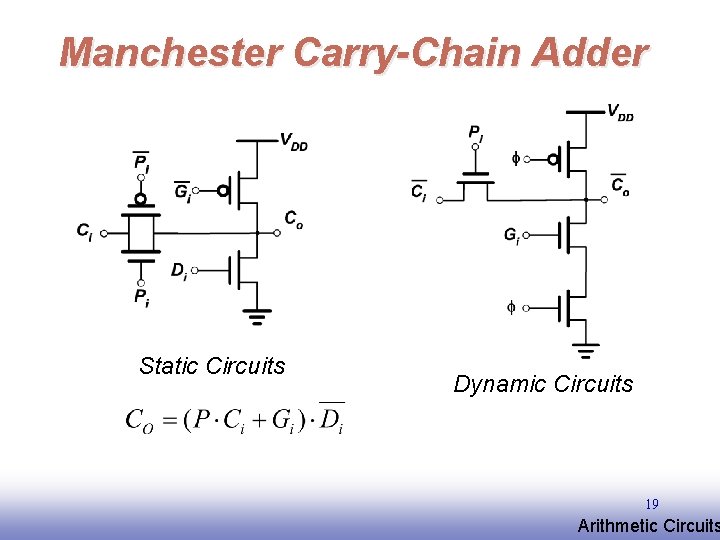
Manchester Carry-Chain Adder Static Circuits Dynamic Circuits 19 EE 141 Arithmetic Circuits

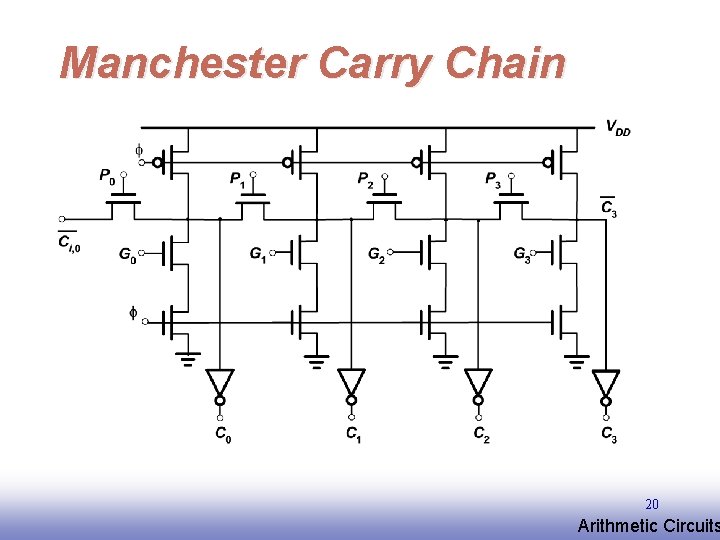
Manchester Carry Chain 20 EE 141 Arithmetic Circuits

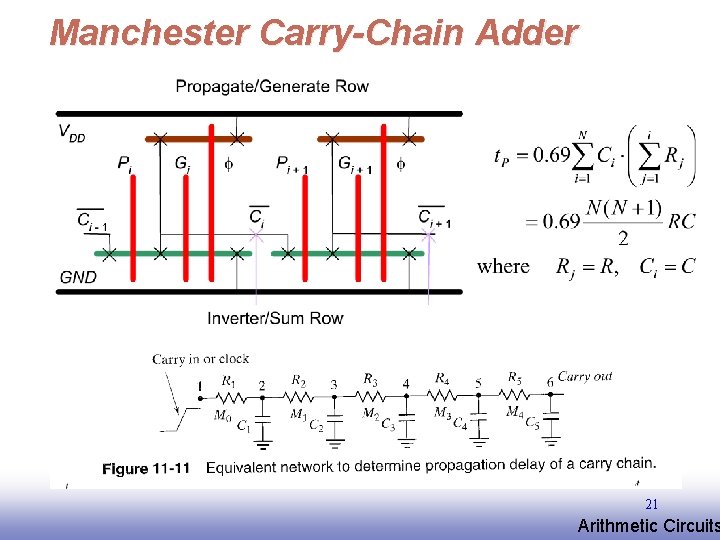
Manchester Carry-Chain Adder 21 EE 141 Arithmetic Circuits

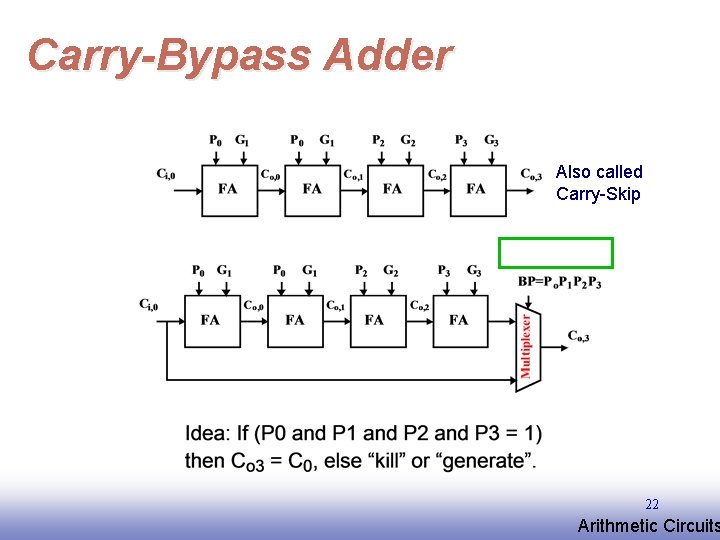
Carry-Bypass Adder Also called Carry-Skip 22 EE 141 Arithmetic Circuits

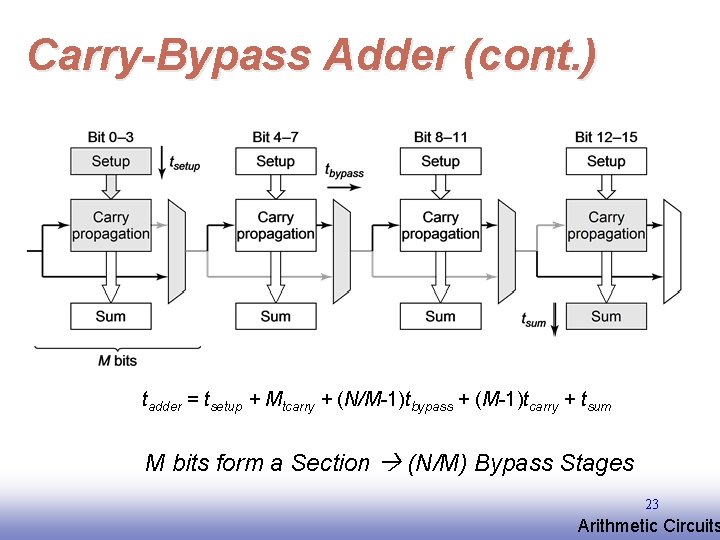
Carry-Bypass Adder (cont. ) tadder = tsetup + Mtcarry + (N/M-1)tbypass + (M-1)tcarry + tsum M bits form a Section (N/M) Bypass Stages 23 EE 141 Arithmetic Circuits

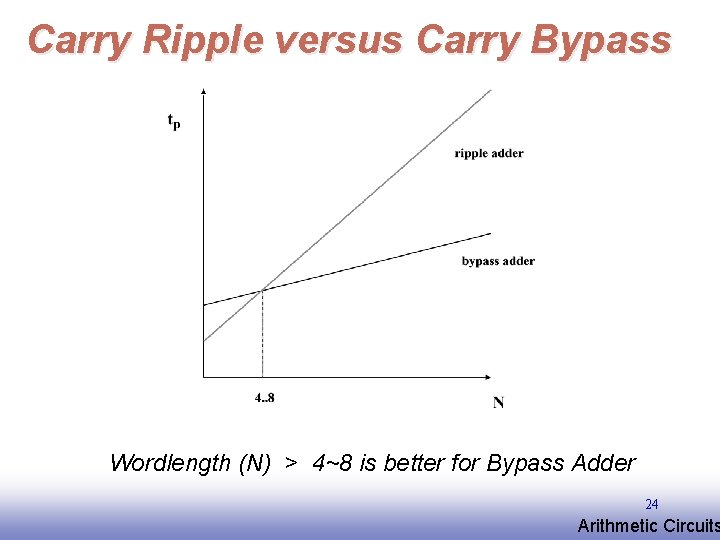
Carry Ripple versus Carry Bypass Wordlength (N) > 4~8 is better for Bypass Adder 24 EE 141 Arithmetic Circuits

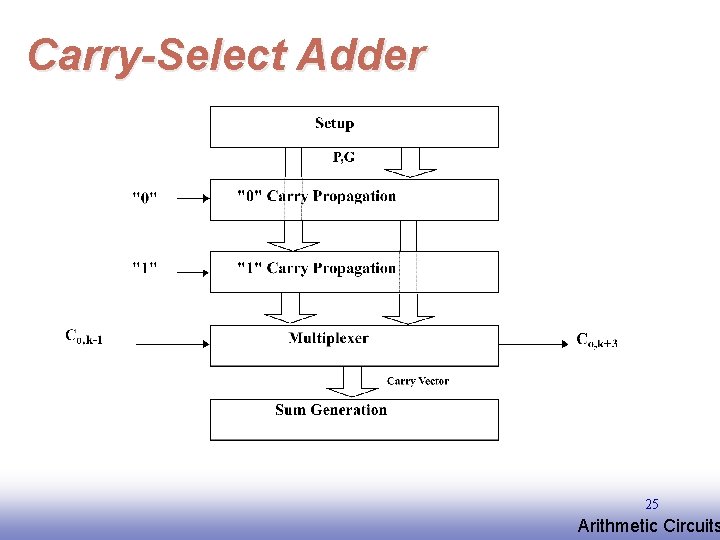
Carry-Select Adder 25 EE 141 Arithmetic Circuits

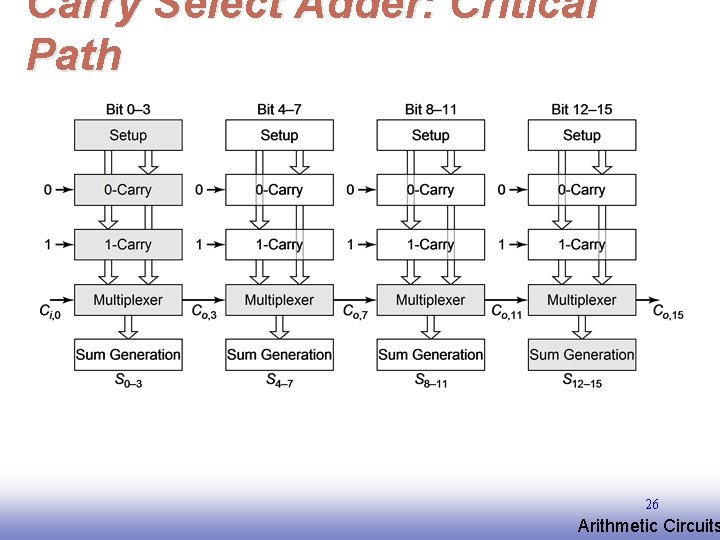
Carry Select Adder: Critical Path 26 EE 141 Arithmetic Circuits

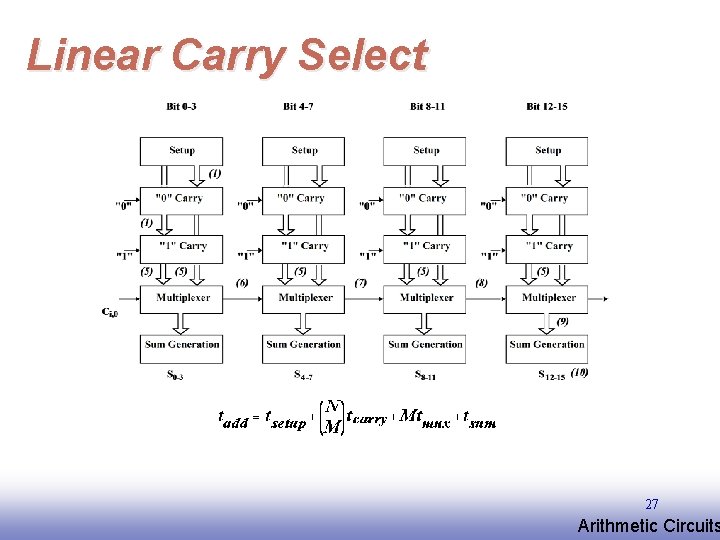
Linear Carry Select 27 EE 141 Arithmetic Circuits

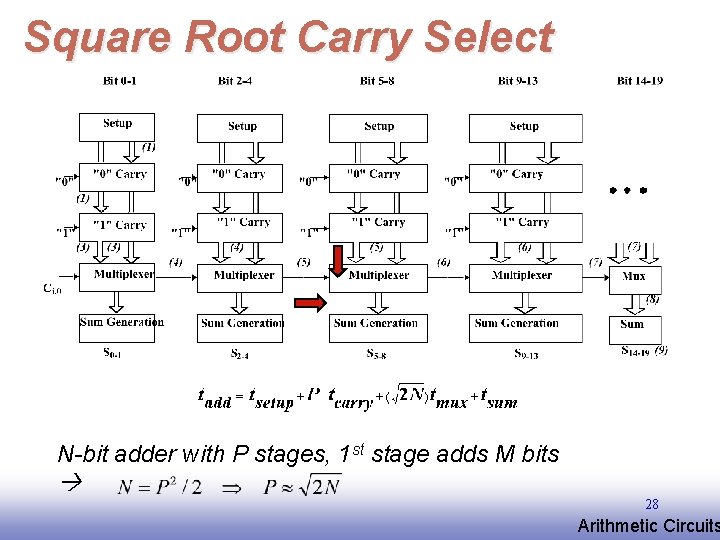
Square Root Carry Select N-bit adder with P stages, 1 st stage adds M bits 28 EE 141 Arithmetic Circuits

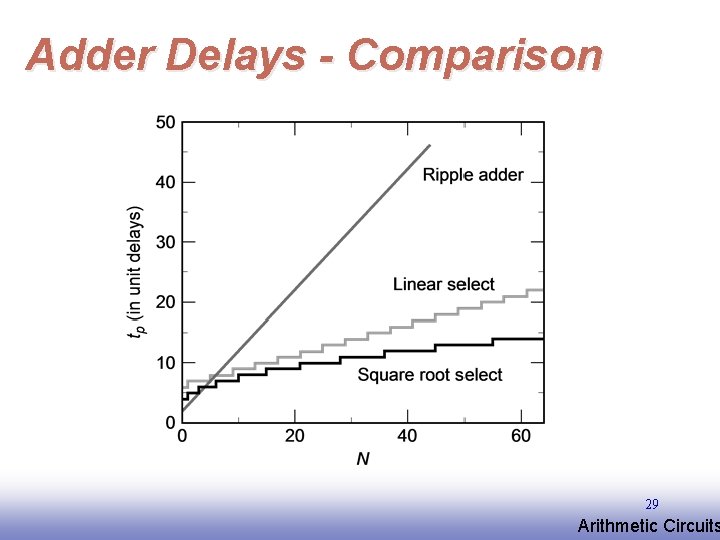
Adder Delays - Comparison 29 EE 141 Arithmetic Circuits

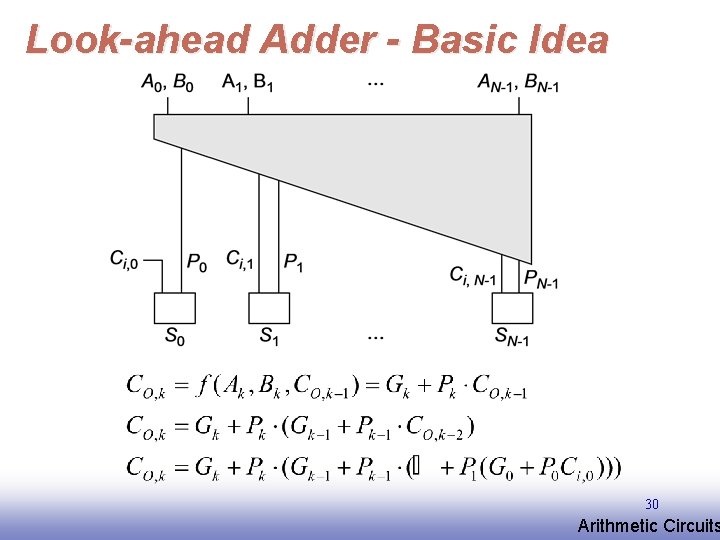
Look-ahead Adder - Basic Idea 30 EE 141 Arithmetic Circuits

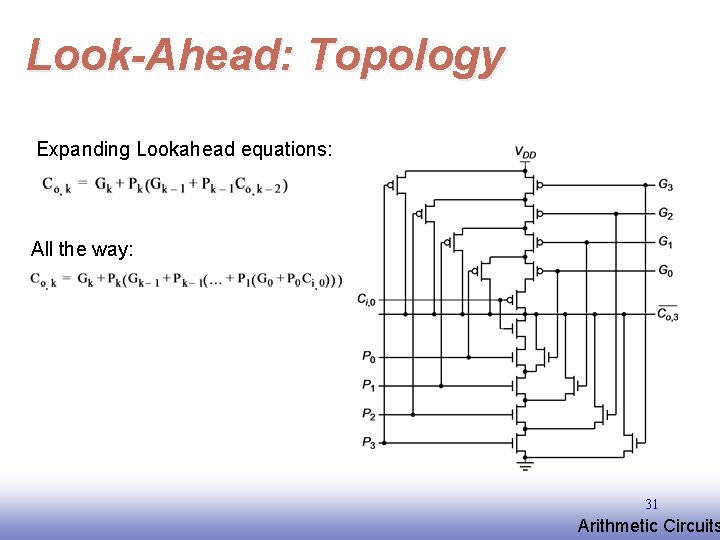
Look-Ahead: Topology Expanding Lookahead equations: All the way: 31 EE 141 Arithmetic Circuits

Multipliers 32 EE 141 Arithmetic Circuits

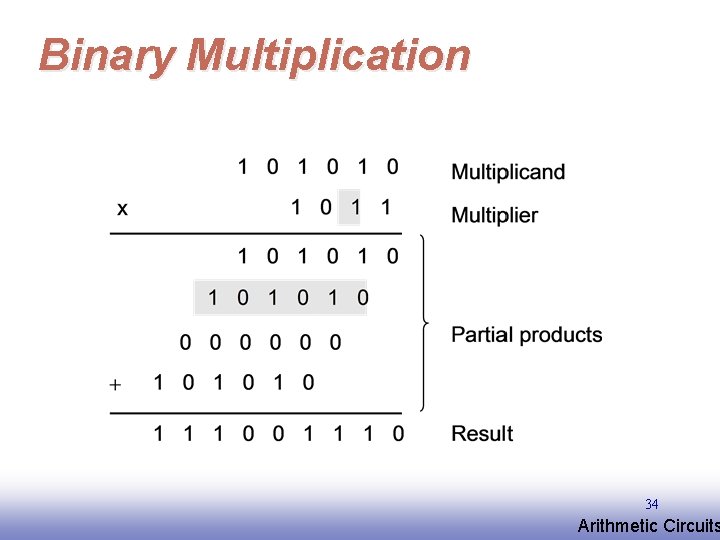
Binary Multiplication 33 EE 141 Arithmetic Circuits

Binary Multiplication 34 EE 141 Arithmetic Circuits

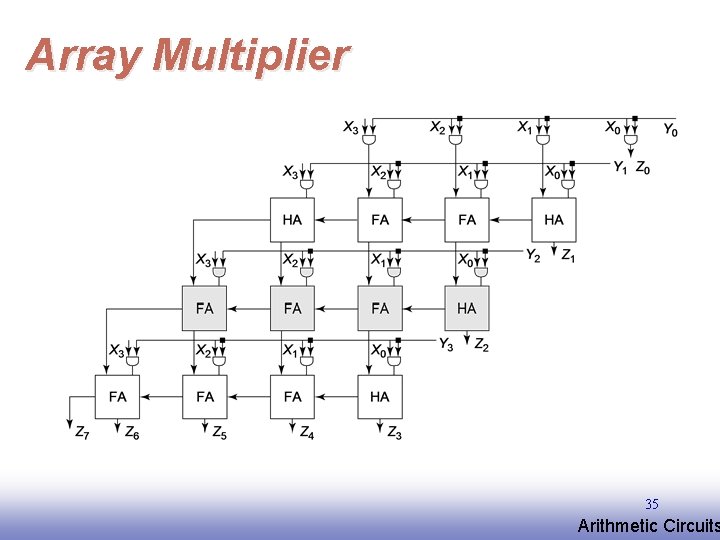
Array Multiplier 35 EE 141 Arithmetic Circuits

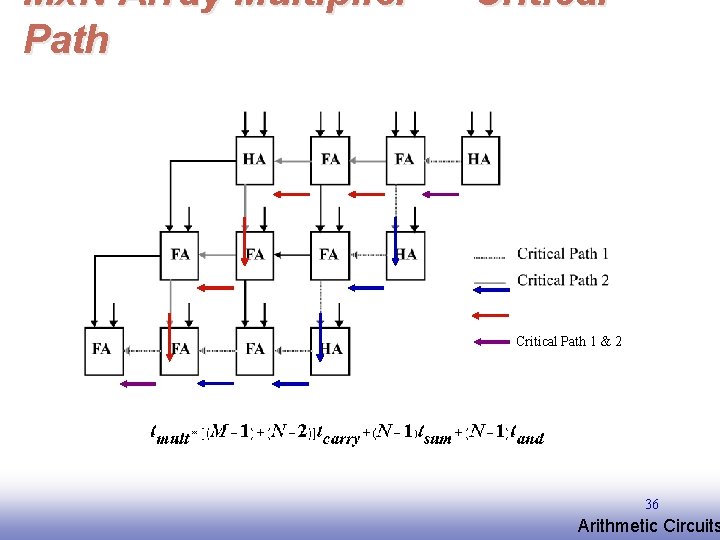
Mx. N Array Multiplier — Critical Path 1 & 2 36 EE 141 Arithmetic Circuits

Carry-Save Multiplier 37 EE 141 Arithmetic Circuits

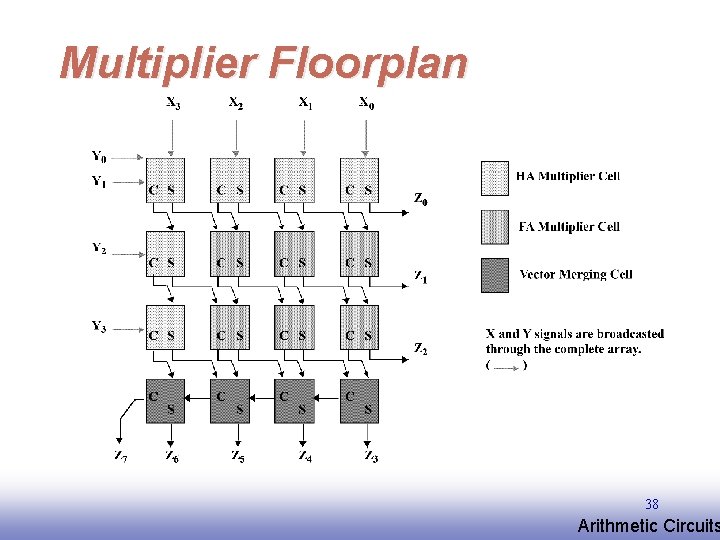
Multiplier Floorplan 38 EE 141 Arithmetic Circuits

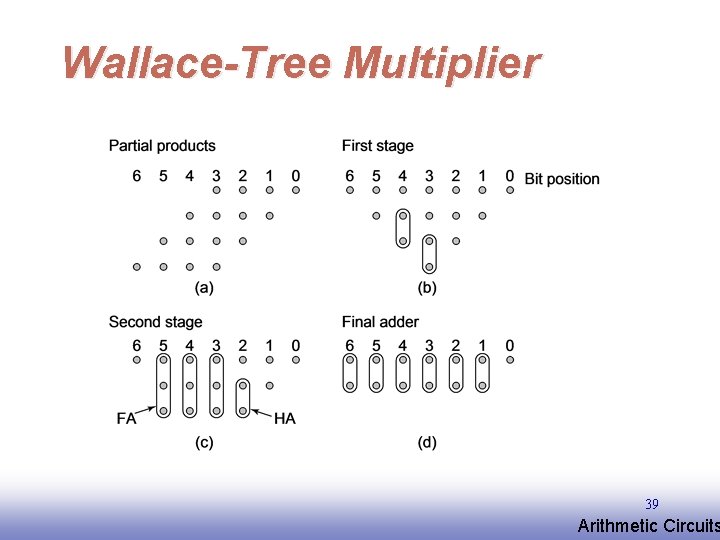
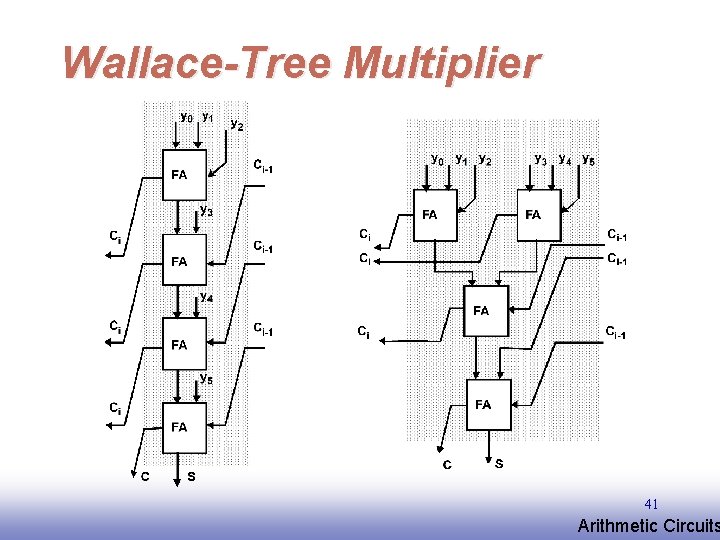
Wallace-Tree Multiplier 39 EE 141 Arithmetic Circuits

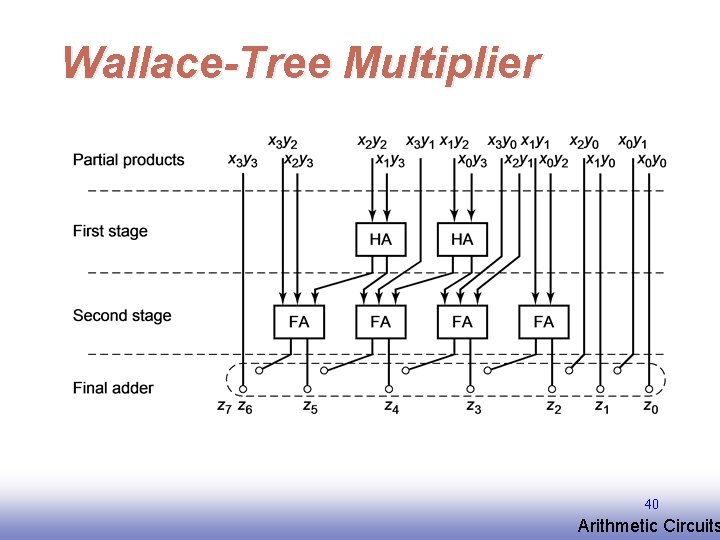
Wallace-Tree Multiplier 40 EE 141 Arithmetic Circuits

Wallace-Tree Multiplier 41 EE 141 Arithmetic Circuits

Multipliers —Summary • Identify Critical Paths • Other Possible techniques: • Data Encoding (Booth) • Logarithmic v. s. Linear (Wallace Tree Multiplier) • Pipelining 42 EE 141 Arithmetic Circuits

Shifters 43 EE 141 Arithmetic Circuits

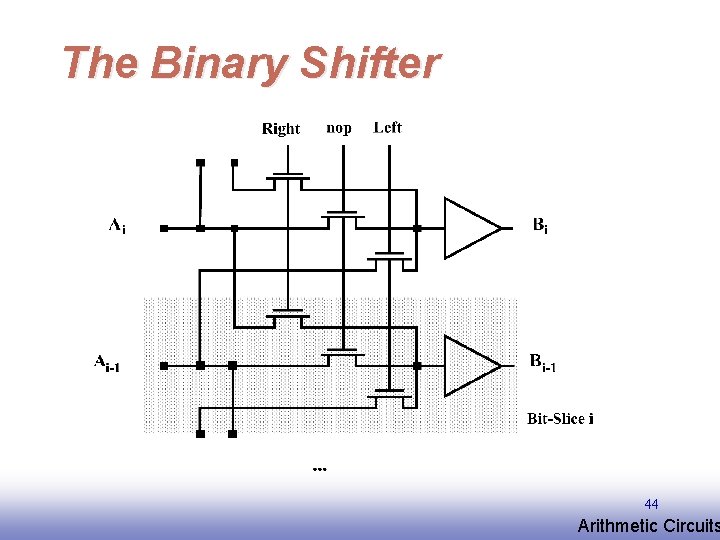
The Binary Shifter 44 EE 141 Arithmetic Circuits

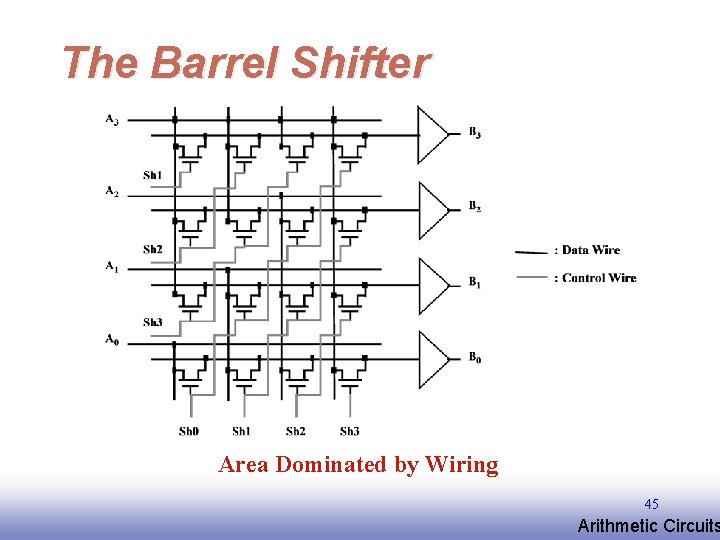
The Barrel Shifter Area Dominated by Wiring 45 EE 141 Arithmetic Circuits

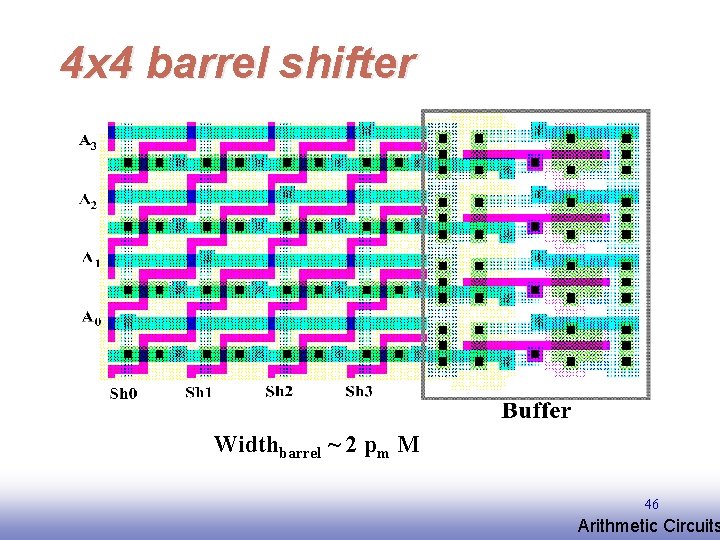
4 x 4 barrel shifter Widthbarrel ~ 2 pm M 46 EE 141 Arithmetic Circuits

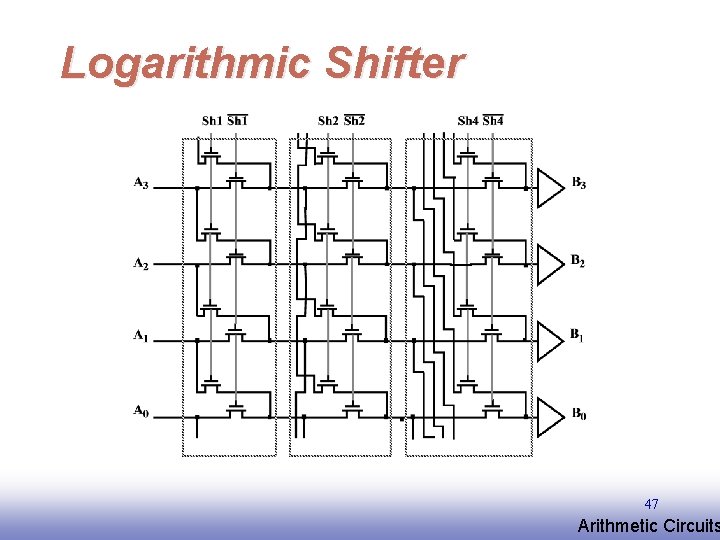
Logarithmic Shifter 47 EE 141 Arithmetic Circuits

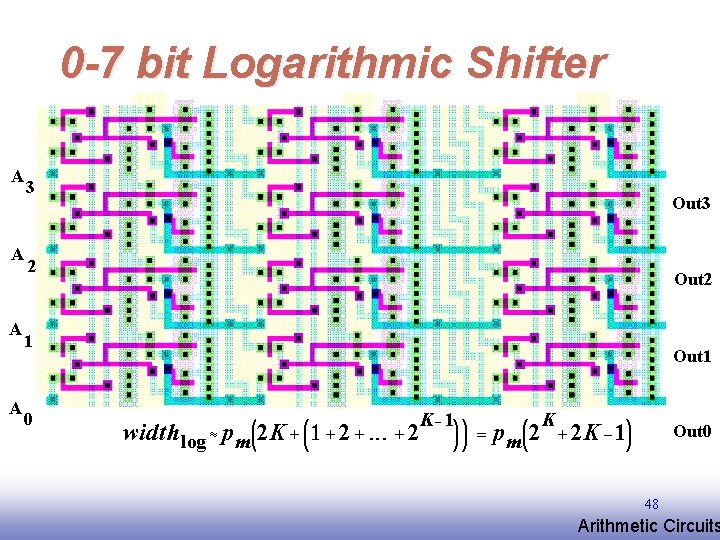
0 -7 bit Logarithmic Shifter A A 3 Out 3 2 Out 2 1 Out 1 0 Out 0 48 EE 141 Arithmetic Circuits

Summary q Datapath designs are fundamentals for highspeed DSP, Multimedia, Communication digital VLSI designs. q Most adders, multipliers, division circuits are now available in Synopsys Designware under different area/speed constraint. q For details, check “Advanced VLSI” notes, or “Computer Arithmetic” textbooks 49 EE 141 Arithmetic Circuits