Chapter 14 Arithmetic Circuits I Adder Designs Rev

Chapter 14 Arithmetic Circuits (I): Adder Designs Rev. 1. 0 05/12/2003 Rev. 2. 0 06/05/2003 Rev. 2. 1 06/12/2003 1 EE 141 Arithmetic Circuits

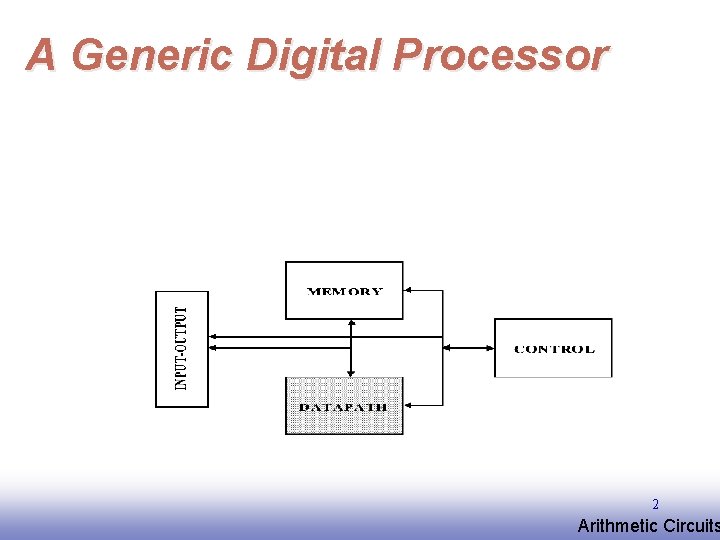
A Generic Digital Processor 2 EE 141 Arithmetic Circuits

Building Blocks for Digital Architectures Arithmetic and Unit - Bit-sliced datapath (adder, multiplier, shifter, comparator, etc. ) Memory - RAM, ROM, Buffers, Shift registers Control - Finite state machine (PLA, random logic. ) - Counters Interconnect - Switches - Arbiters - Bus 3 EE 141 Arithmetic Circuits

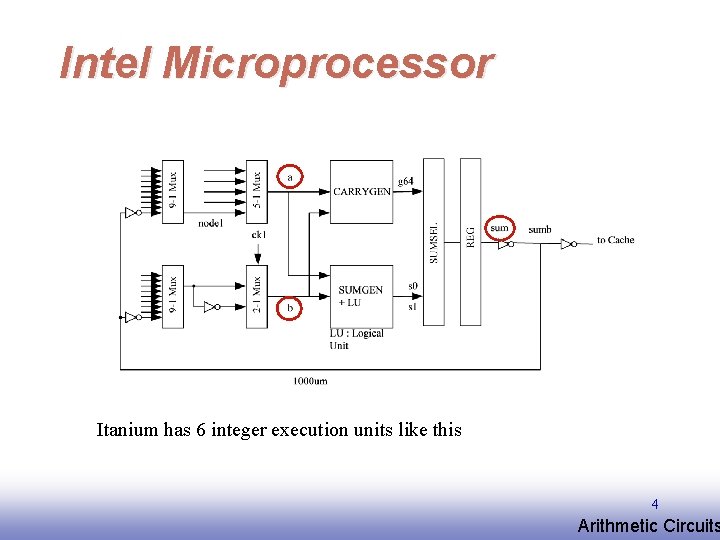
Intel Microprocessor Itanium has 6 integer execution units like this 4 EE 141 Arithmetic Circuits

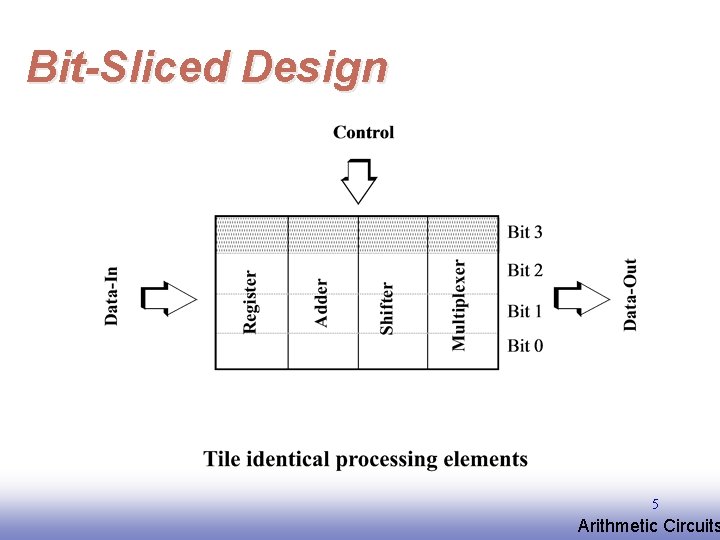
Bit-Sliced Design 5 EE 141 Arithmetic Circuits

Itanium Integer Datapath EE 141 Fetzer, Orton, ISSCC’ 02 6 Arithmetic Circuits

Adders 7 EE 141 Arithmetic Circuits

Several Implementations of Adders q q q q One-Bit Full Adder (Cell) Carry-Ripple Adder Bit-Serial Adder Mirror Adder Transmission-Gate Adder Manchester Adder Carry lookahead Adder Carry-Select Adder 8 EE 141 Arithmetic Circuits

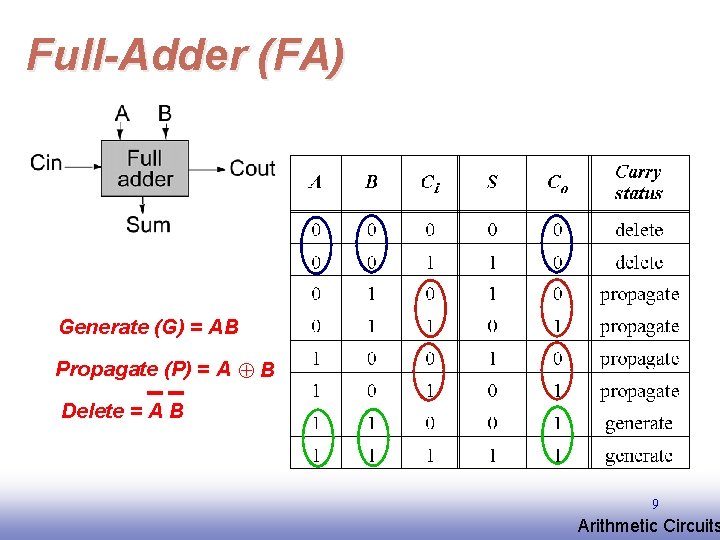
Full-Adder (FA) Generate (G) = AB Propagate (P) = A B Delete = A B 9 EE 141 Arithmetic Circuits

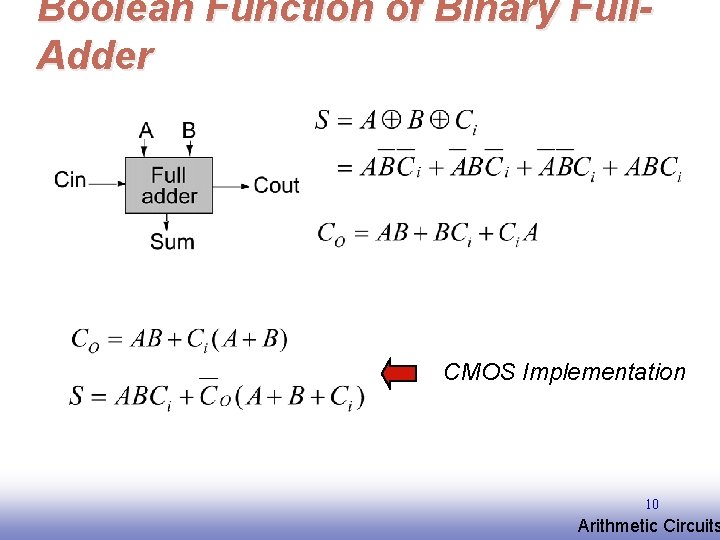
Boolean Function of Binary Full. Adder CMOS Implementation 10 EE 141 Arithmetic Circuits

Express Sum and Carry as a function of P, G, D Define 3 new variable which ONLY depend on A, B Generate (G) = AB Propagate (P) = A B Delete = A B Can also derive expressions for S and Co based on D and P Note that we will be sometimes using an alternate definition for Propagate (P) = A + B 11 EE 141 Arithmetic Circuits

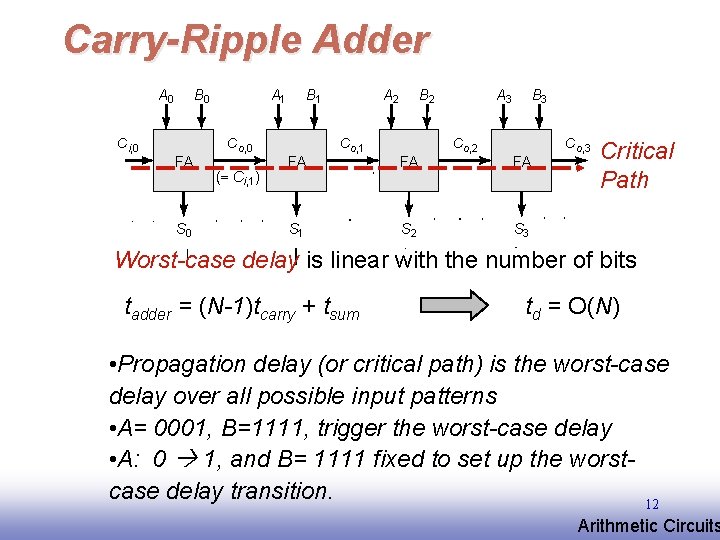
Carry-Ripple Adder A 0 Ci, 0 B 0 FA S 0 A 1 Co, 0 (= Ci, 1) B 1 FA A 2 Co, 1 S 1 B 2 FA S 2 A 3 Co, 2 B 3 FA Co, 3 Critical Path S 3 Worst-case delay is linear with the number of bits tadder = (N-1)tcarry + tsum td = O(N) • Propagation delay (or critical path) is the worst-case delay over all possible input patterns • A= 0001, B=1111, trigger the worst-case delay • A: 0 1, and B= 1111 fixed to set up the worstcase delay transition. 12 EE 141 Arithmetic Circuits

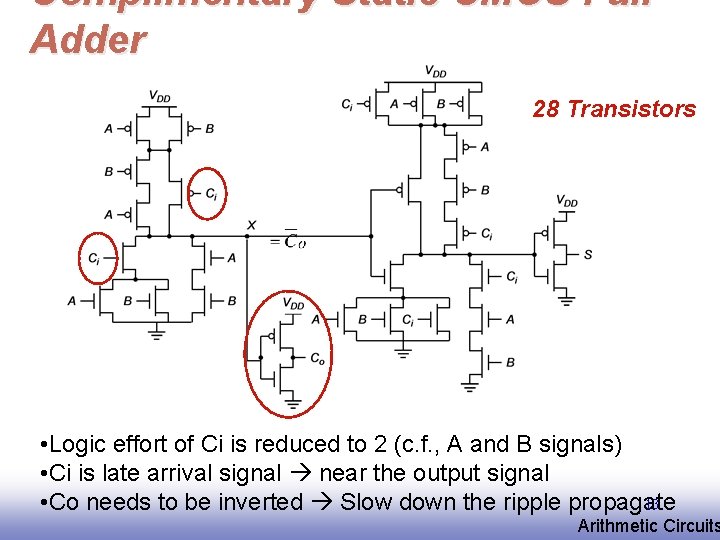
Complimentary Static CMOS Full Adder 28 Transistors • Logic effort of Ci is reduced to 2 (c. f. , A and B signals) • Ci is late arrival signal near the output signal 13 • Co needs to be inverted Slow down the ripple propagate EE 141 Arithmetic Circuits

Inversion Property 14 EE 141 Arithmetic Circuits

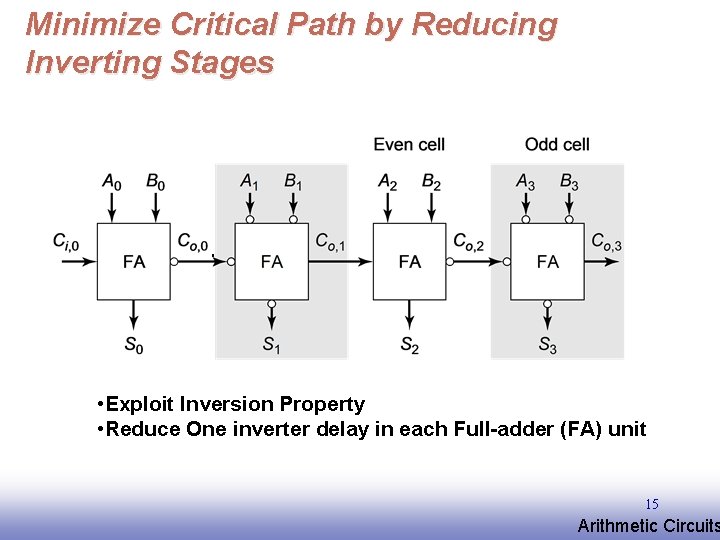
Minimize Critical Path by Reducing Inverting Stages • Exploit Inversion Property • Reduce One inverter delay in each Full-adder (FA) unit 15 EE 141 Arithmetic Circuits

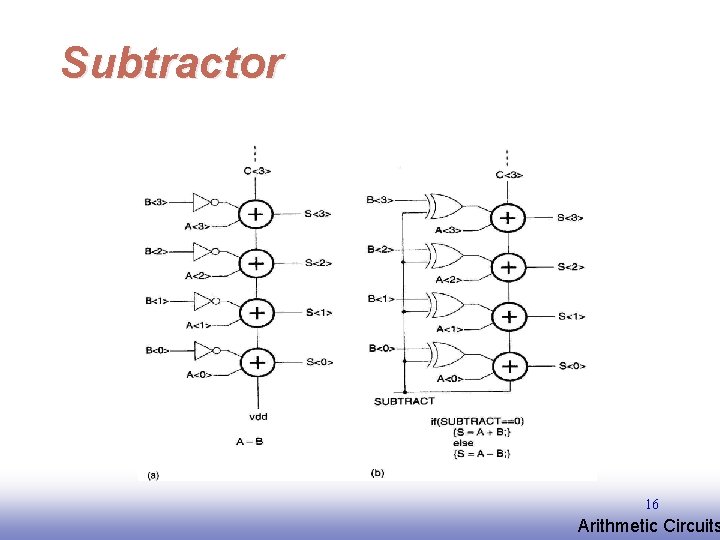
Subtractor 16 EE 141 Arithmetic Circuits

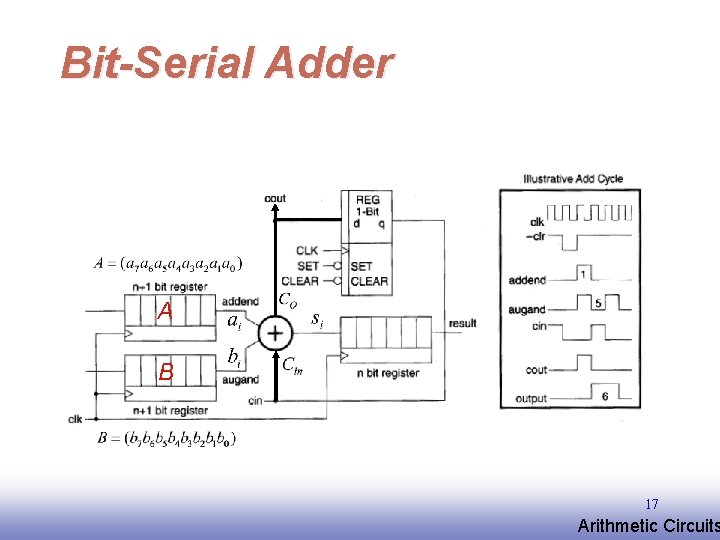
Bit-Serial Adder A B 17 EE 141 Arithmetic Circuits

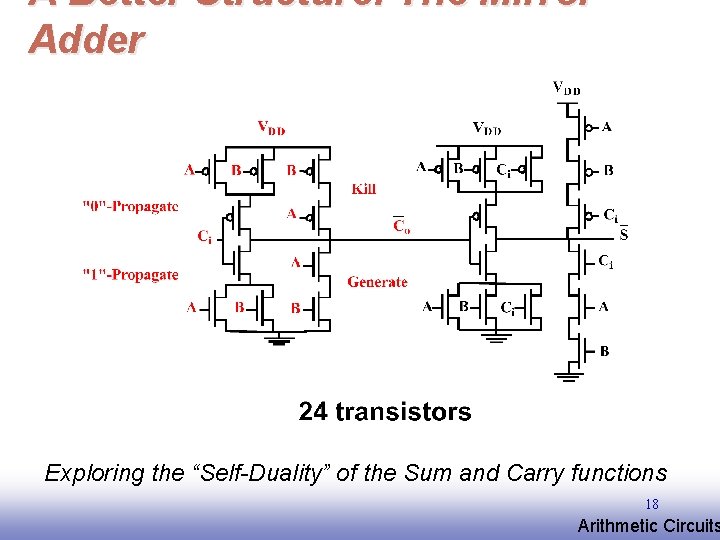
A Better Structure: The Mirror Adder Exploring the “Self-Duality” of the Sum and Carry functions 18 EE 141 Arithmetic Circuits

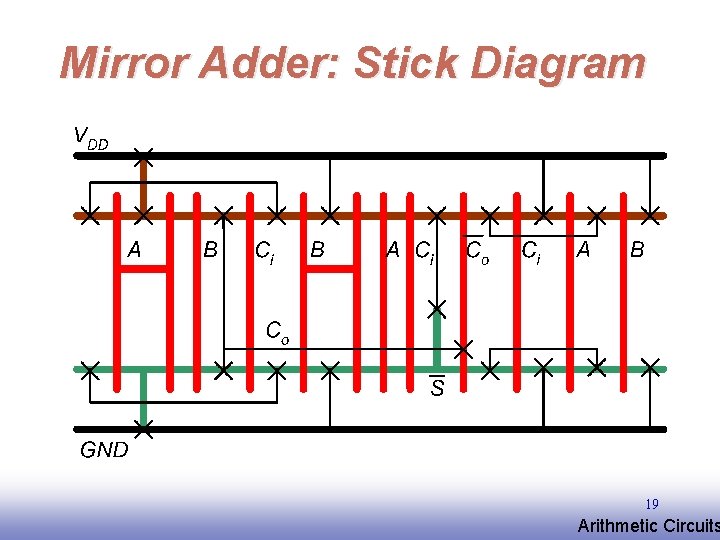
Mirror Adder: Stick Diagram 19 EE 141 Arithmetic Circuits

Mirror Adder Design • The NMOS and PMOS chains are completely symmetrical • A maximum of two series transistors can be observed in the carry-generation circuitry for good speed. • When laying out the cell, the most critical issue is the minimization of the capacitance at node Co. • The capacitance at node Co is composed of four diffusion capacitances, two internal gate capacitances, and six gate capacitances in the connecting adder cell. • The transistors connected to Ci are placed closest to the output. 20 EE 141 Arithmetic Circuits

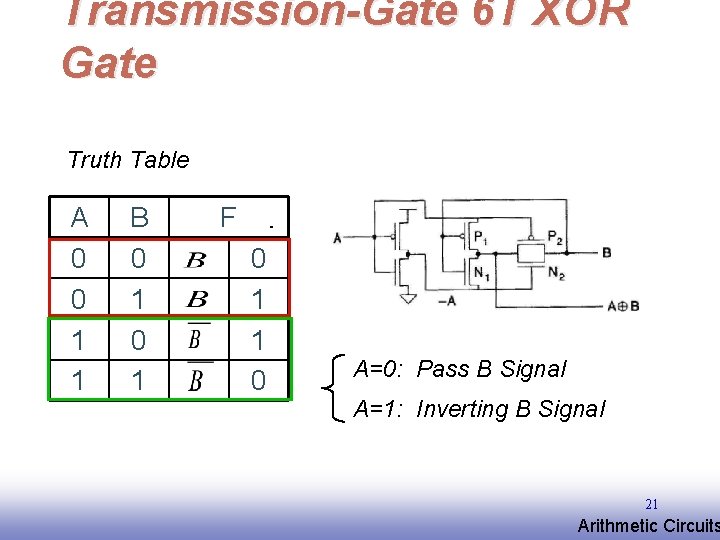
Transmission-Gate 6 T XOR Gate Truth Table A 0 0 1 1 B 0 1 F 0 1 1 0 A=0: Pass B Signal A=1: Inverting B Signal 21 EE 141 Arithmetic Circuits

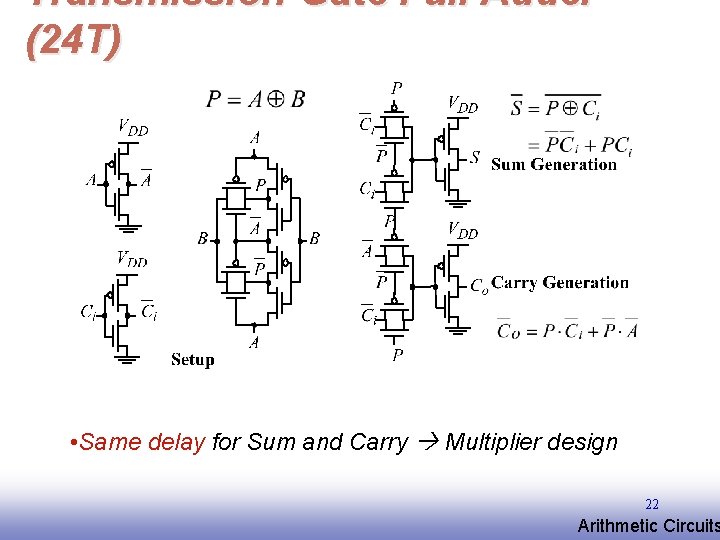
Transmission-Gate Full Adder (24 T) • Same delay for Sum and Carry Multiplier design 22 EE 141 Arithmetic Circuits

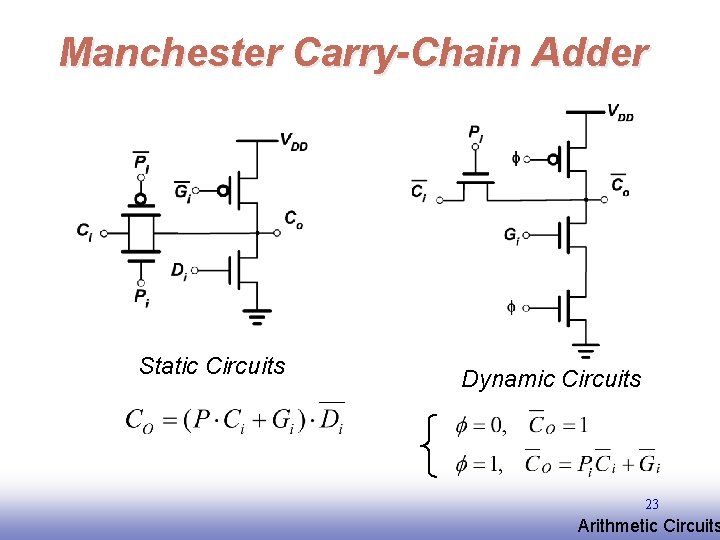
Manchester Carry-Chain Adder Static Circuits Dynamic Circuits 23 EE 141 Arithmetic Circuits

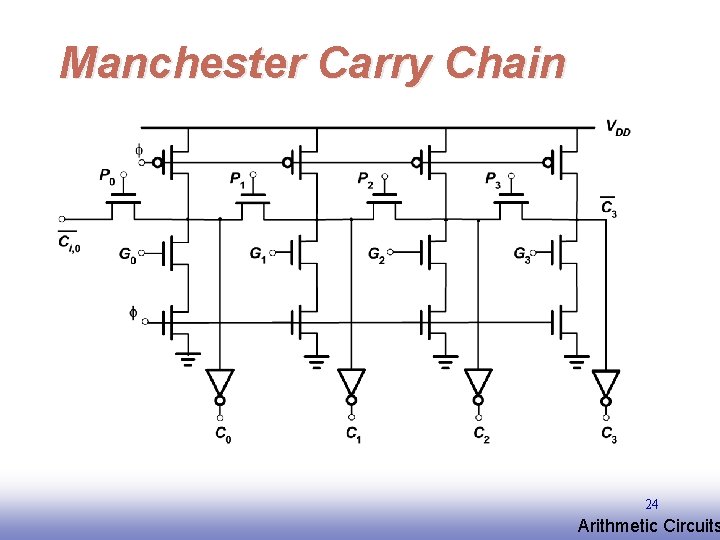
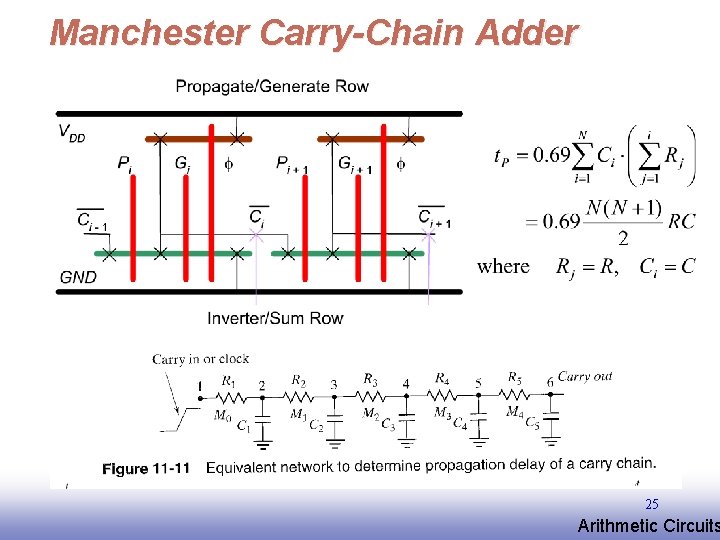
Manchester Carry Chain 24 EE 141 Arithmetic Circuits

Manchester Carry-Chain Adder 25 EE 141 Arithmetic Circuits

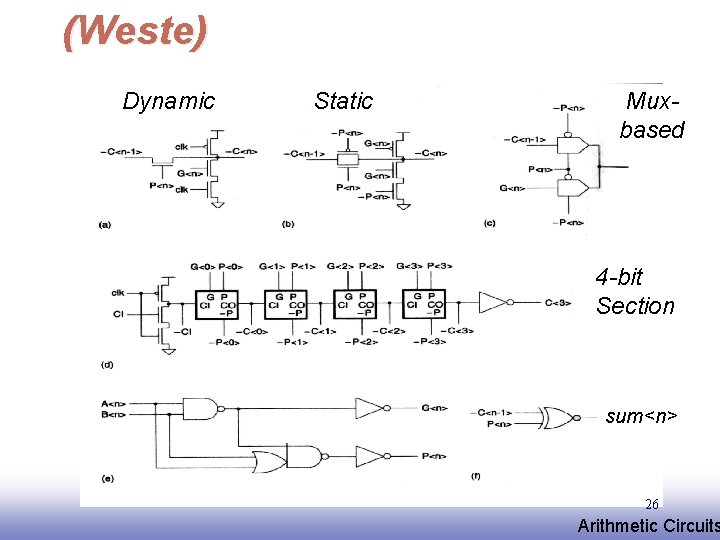
(Weste) Dynamic Static Muxbased 4 -bit Section sum<n> 26 EE 141 Arithmetic Circuits

Manchester Adder Circuits (Cont. ) q Dynamic stage § When CLK is low, the output node is pre-charged by the p pull-up transistor. § When CLK goes high, the pull-down transistor turns on. § If carry generate G=AB is true the output node discharges. § If carry propagate P=A+B is true a previous carry may be coupled to the output node, conditionally discharging it. q Static stage § This requires P to be generated as A B § The Manchester adder stage improves on the carrylookahead implementation. 27 EE 141 Arithmetic Circuits

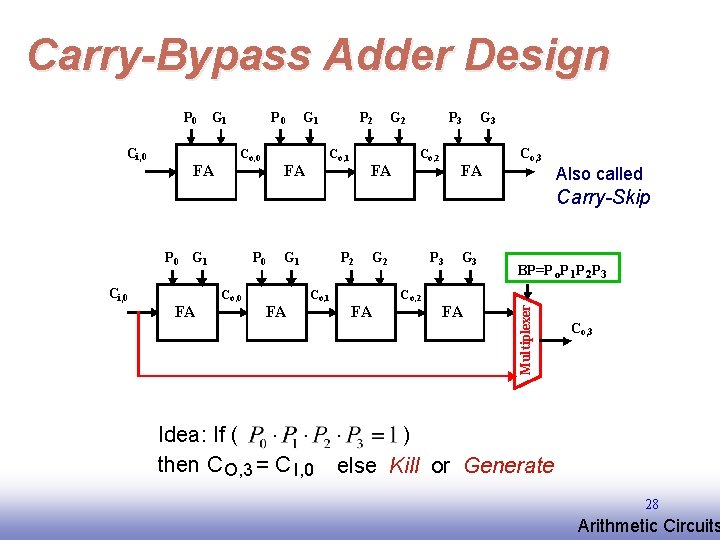
Carry-Bypass Adder Design P 0 Ci, 0 G 1 FA P 0 C o, 0 G 1 P 2 C o, 1 FA G 2 FA P 3 Co, 2 G 3 FA Co, 3 Also called Carry-Skip Ci, 0 FA P 0 C o, 0 G 1 FA P 2 Co, 1 Idea: If ( then C O, 3 = C I, 0 G 2 FA P 3 C o, 2 G 3 FA BP=P o. P 1 P 2 P 3 Multiplexer P 0 G 1 Co, 3 ) else Kill or Generate 28 EE 141 Arithmetic Circuits

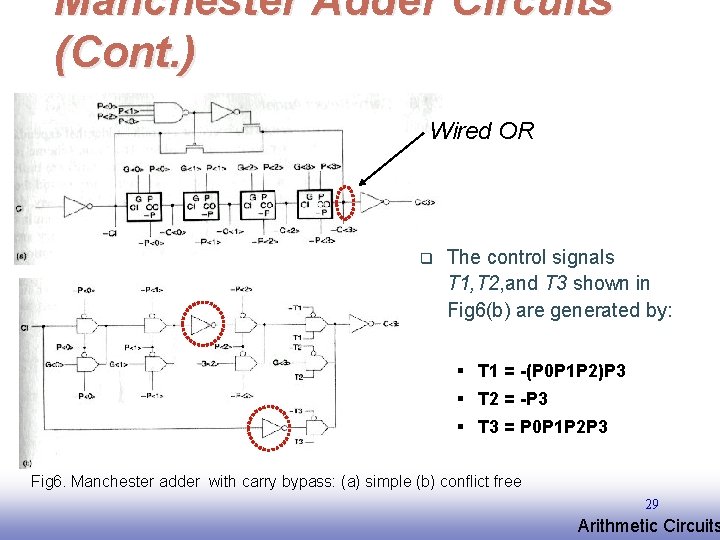
Manchester Adder Circuits (Cont. ) Wired OR q The control signals T 1, T 2, and T 3 shown in Fig 6(b) are generated by: § T 1 = -(P 0 P 1 P 2)P 3 § T 2 = -P 3 § T 3 = P 0 P 1 P 2 P 3 Fig 6. Manchester adder with carry bypass: (a) simple (b) conflict free 29 EE 141 Arithmetic Circuits

Manchester Adder Circuits (Cont. ) q The worst case propagation time of a Manchester adder can be improved by bypassing the four stages if all carry-propagate signals are true. q Fig. 6(b) uses a “conflict -free” bypass circuit, which improves the speed by using a 3 -input multiplexer that prevents conflicts at the wired OR node in the adder. q In Fig. 6(b), the inverter presented on the Cin signal has been moved to the center of the carry chain to improve speed. 30 EE 141 Arithmetic Circuits

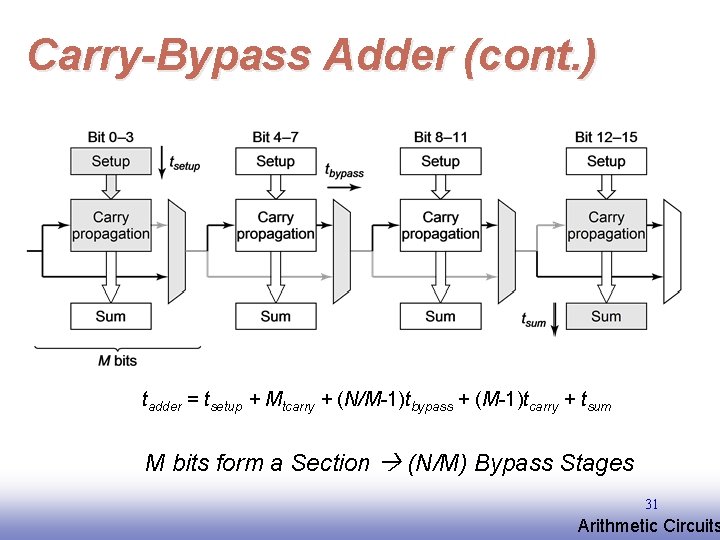
Carry-Bypass Adder (cont. ) tadder = tsetup + Mtcarry + (N/M-1)tbypass + (M-1)tcarry + tsum M bits form a Section (N/M) Bypass Stages 31 EE 141 Arithmetic Circuits

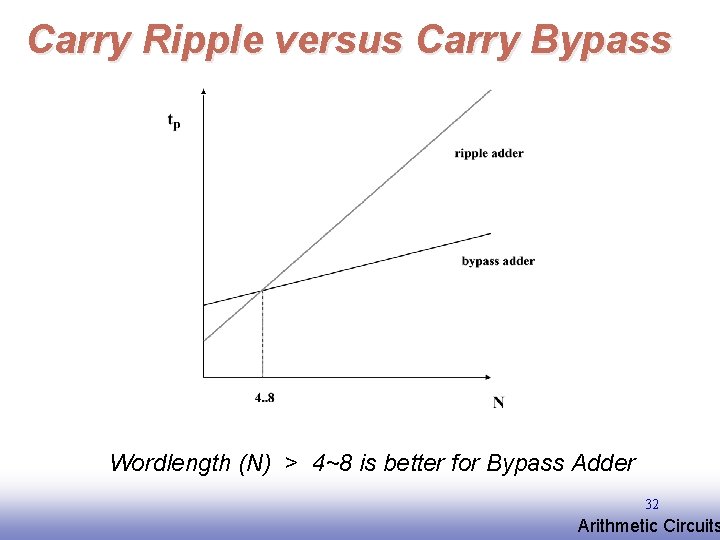
Carry Ripple versus Carry Bypass Wordlength (N) > 4~8 is better for Bypass Adder 32 EE 141 Arithmetic Circuits

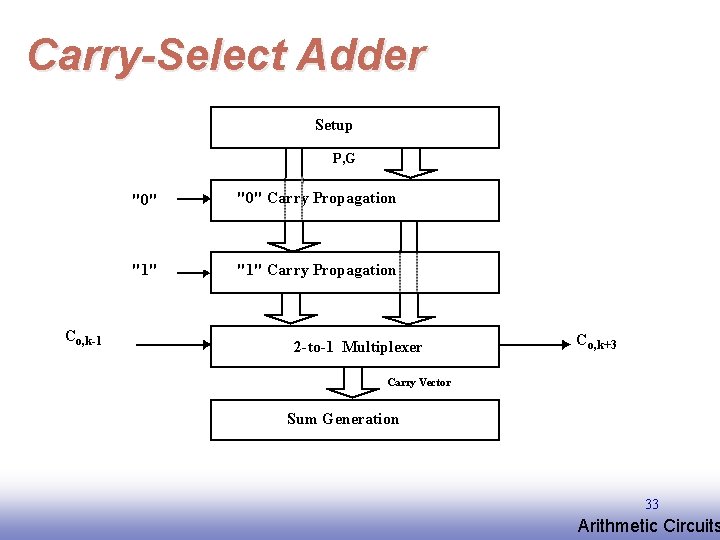
Carry-Select Adder Setup P, G Co, k-1 "0" Carry Propagation "1" Carry Propagation 2 -to-1 Multiplexer Co, k+3 Carry Vector Sum Generation 33 EE 141 Arithmetic Circuits

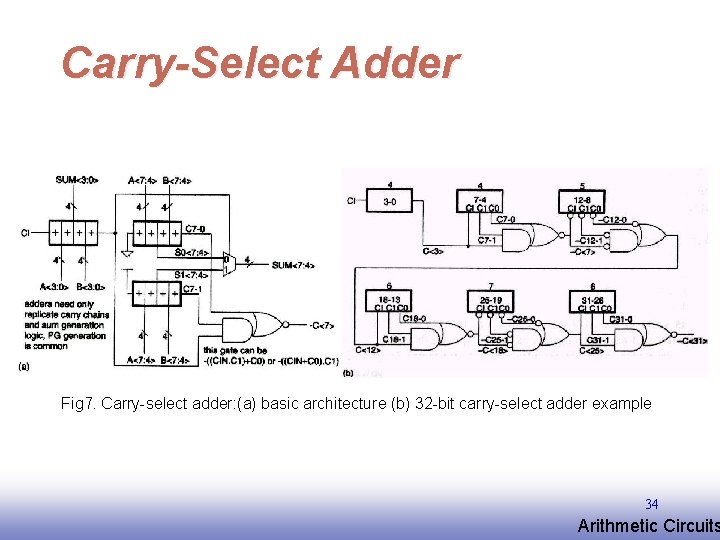
Carry-Select Adder Fig 7. Carry-select adder: (a) basic architecture (b) 32 -bit carry-select adder example 34 EE 141 Arithmetic Circuits

Carry Select Adder: Critical Path 35 EE 141 Arithmetic Circuits

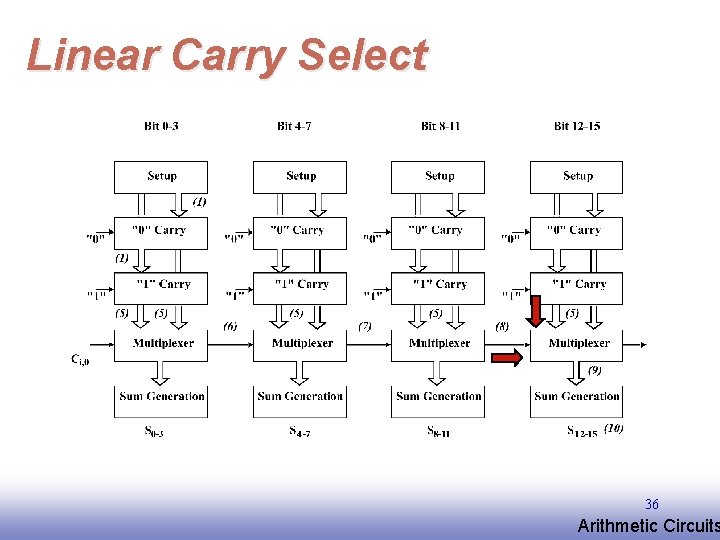
Linear Carry Select 36 EE 141 Arithmetic Circuits

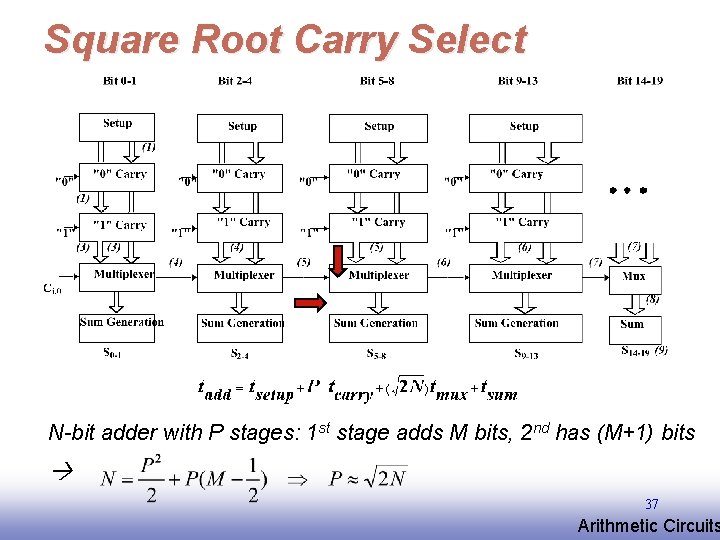
Square Root Carry Select N-bit adder with P stages: 1 st stage adds M bits, 2 nd has (M+1) bits 37 EE 141 Arithmetic Circuits

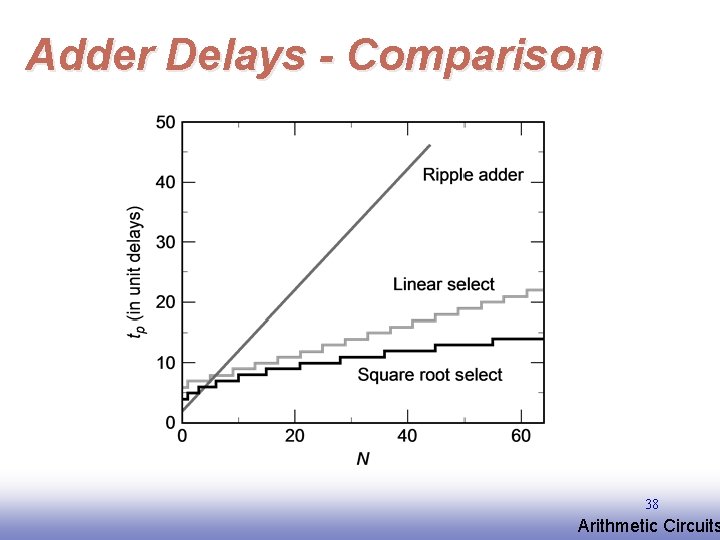
Adder Delays - Comparison 38 EE 141 Arithmetic Circuits

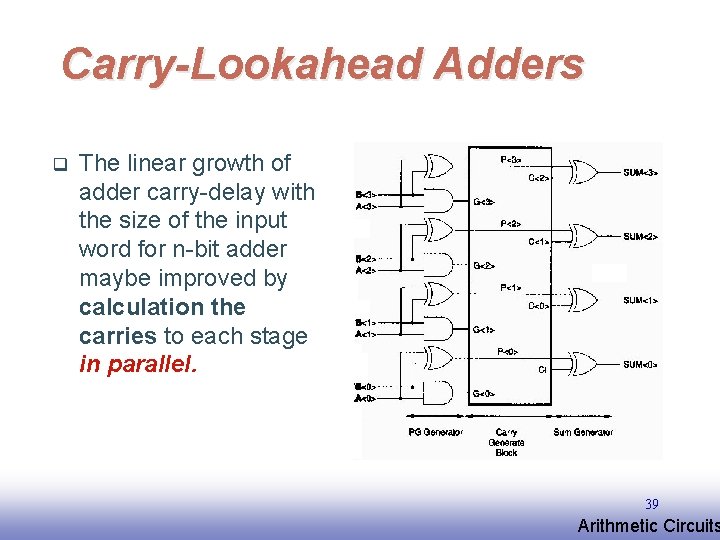
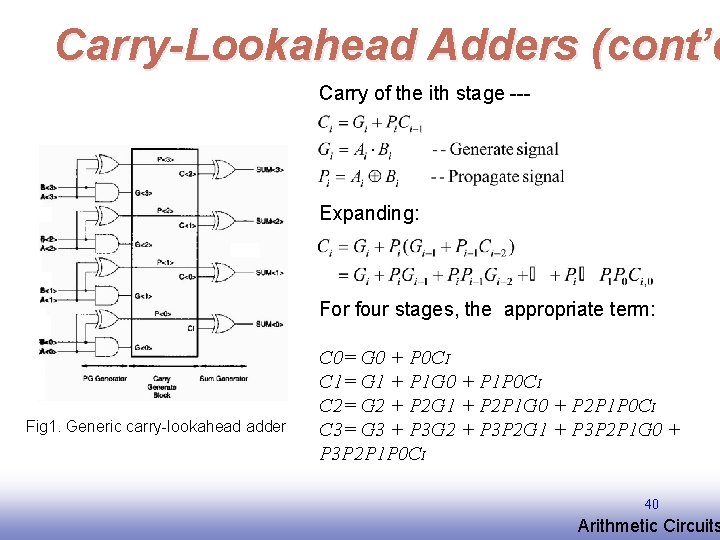
Carry-Lookahead Adders q The linear growth of adder carry-delay with the size of the input word for n-bit adder maybe improved by calculation the carries to each stage in parallel. 39 EE 141 Arithmetic Circuits

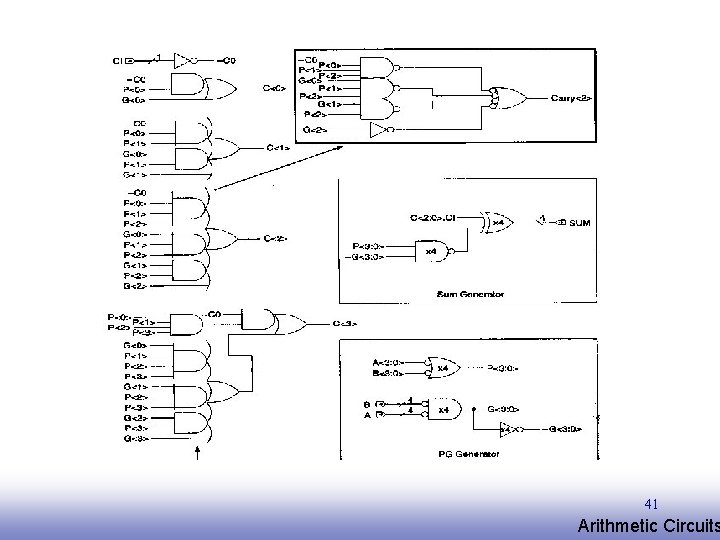
Carry-Lookahead Adders (cont’d Carry of the ith stage --- Expanding: For four stages, the appropriate term: Fig 1. Generic carry-lookahead adder C 0= G 0 + P 0 CI C 1= G 1 + P 1 G 0 + P 1 P 0 CI C 2= G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 CI C 3= G 3 + P 3 G 2 + P 3 P 2 G 1 + P 3 P 2 P 1 G 0 + P 3 P 2 P 1 P 0 CI 40 EE 141 Arithmetic Circuits

41 EE 141 Arithmetic Circuits

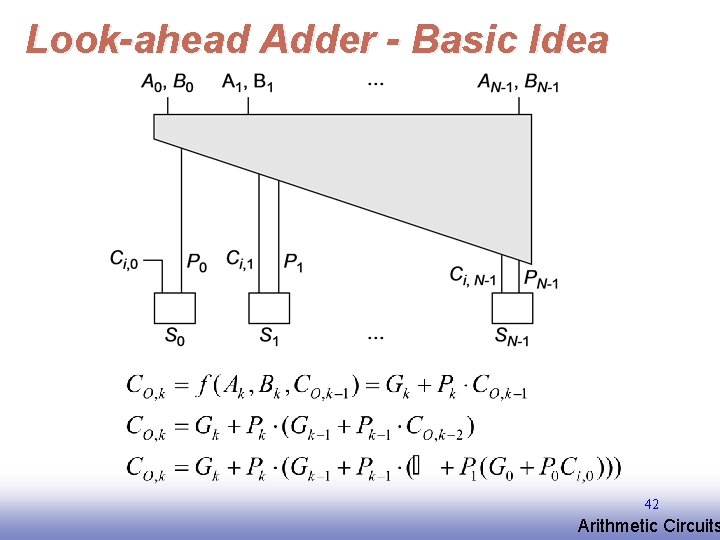
Look-ahead Adder - Basic Idea 42 EE 141 Arithmetic Circuits

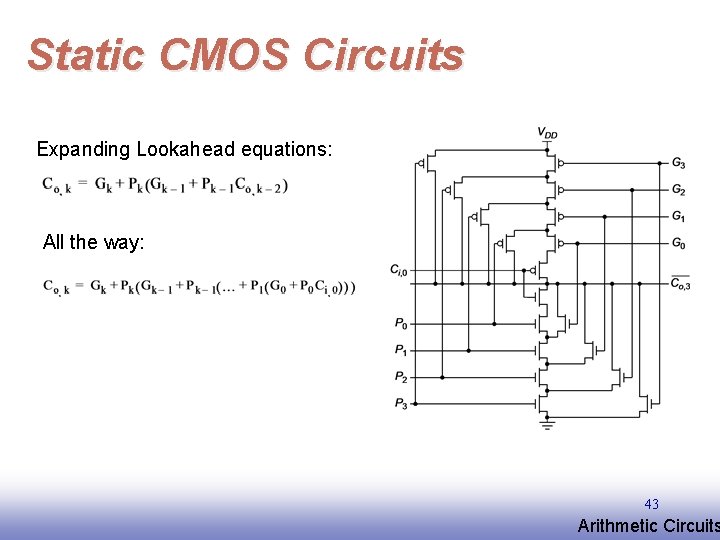
Static CMOS Circuits Expanding Lookahead equations: All the way: 43 EE 141 Arithmetic Circuits

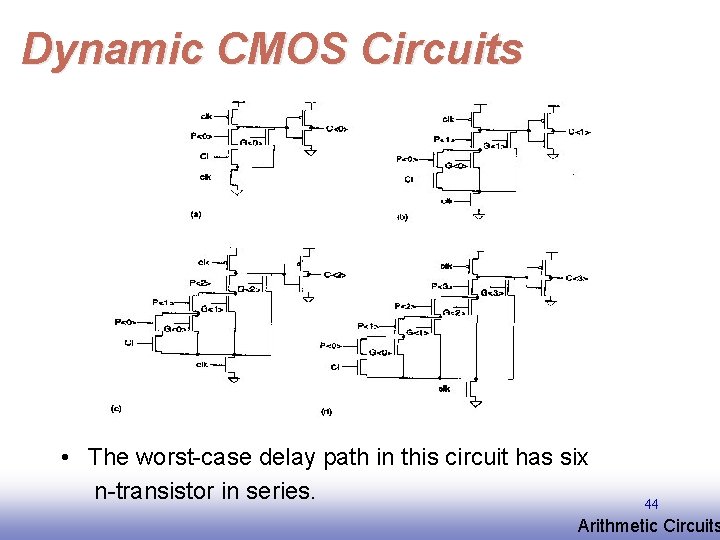
Dynamic CMOS Circuits • The worst-case delay path in this circuit has six n-transistor in series. EE 141 44 Arithmetic Circuits

Carry-Lookahead Adders • Size and fan-in of the gates needed to implement this carry-lookahead scheme can clearly get out of hand • Number of stages of lookahead is usually limited to about 4. • The circuit and layout are quite irregular compared with ripple adder designs. 45 EE 141 Arithmetic Circuits

Summary q Datapath designs are fundamentals for highspeed DSP, Multimedia, Communication digital VLSI designs. q Most adders, multipliers, division circuits are now available in Synopsys Designware under different area/speed constraint. q For details, check “Advanced VLSI” notes, or “Computer Arithmetic” textbooks 46 EE 141 Arithmetic Circuits