Chapter 14 Area Pythagorean Theorem and Volume Copyright

Chapter 14 Area, Pythagorean Theorem, and Volume Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

14 -5 Volume, Mass, and Temperature § § § § Volume of Right Rectangular Prisms Converting Metric Measures of Volume Converting English Measures of Volumes of Prisms and Cylinders Volumes of Pyramids and Cones Volume of a Sphere Mass Relationships Among Metric Units of Volume, Capacity, and Mass § Temperature Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Volume and Surface Area What is the volume of each figure? 9 cubic units What is the surface area of each figure? 34 square units Copyright © 2013, 2010, and 2007, Pearson Education, Inc. 36 square units

Volume of Right Rectangular Prisms Right rectangular prism Volume = wh Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

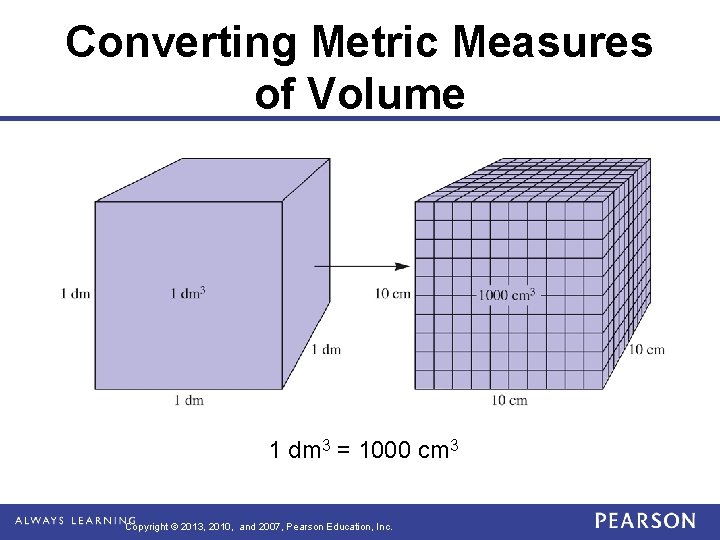
Converting Metric Measures of Volume 1 dm 3 = 1000 cm 3 Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

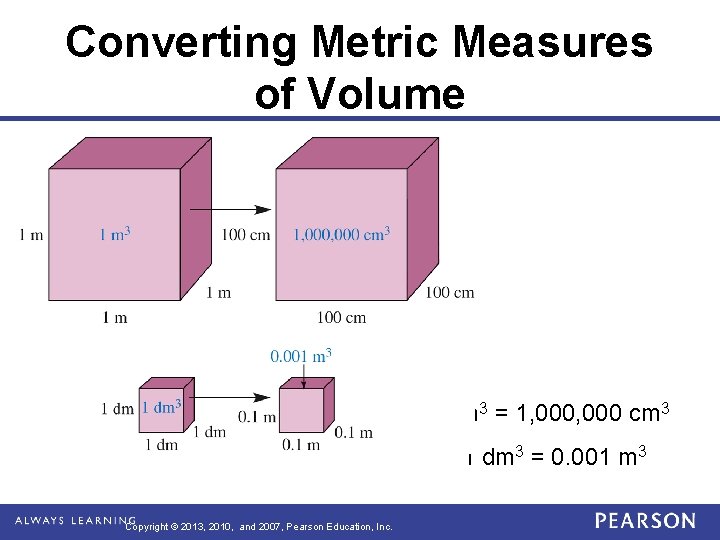
Converting Metric Measures of Volume 1 m 3 = 1, 000 cm 3 1 dm 3 = 0. 001 m 3 Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -18 Convert each of the following: 5, 000 a. 5 m 3 = _______ cm 3 3 12. 3 b. 12, 300 mm 3 = _______cm Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

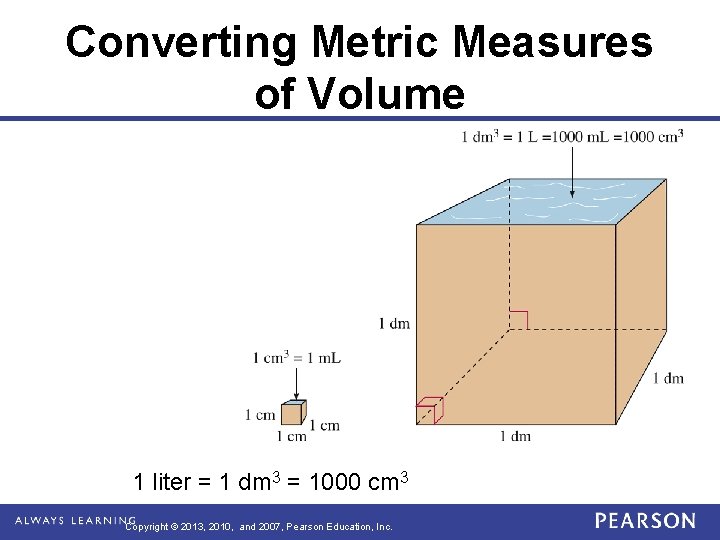
Converting Metric Measures of Volume 1 liter = 1 dm 3 = 1000 cm 3 Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

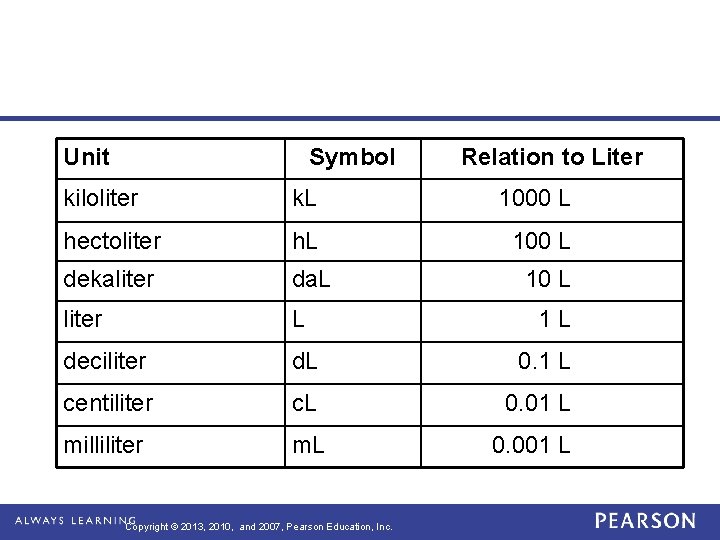
Unit Symbol Relation to Liter kiloliter k. L 1000 L hectoliter h. L 100 L dekaliter da. L 10 L liter L deciliter d. L 0. 1 L centiliter c. L 0. 01 L milliliter m. L 0. 001 L Copyright © 2013, 2010, and 2007, Pearson Education, Inc. 1 L

Example 14 -19 Convert each of the following: 27, 000 m. L a. 27 L = _____ 0. 362 L b. 362 m. L = _____ 3 cm 3 c. 3 m. L = _____ 3000 L d. 3 m 3 = _____ Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Converting English Measures of Volume Basic Units of Volume: cubic inch (in. 3) cubic foot (ft 3) cubic yard (yd 3) Volume equivalents: 1 gal = 231 in. 3 1 qt = gal Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -20 Convert each of the following: a. 45 yd 3 = _____ ft 3 b. 4320 in. 3 = _____ yd 3 Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -20 c. 10 gal = _____ ft 3 d. 3 ft 3 = _____ yd 3 Copyright © 2013, 2010, and 2007, Pearson Education, Inc. (continued)

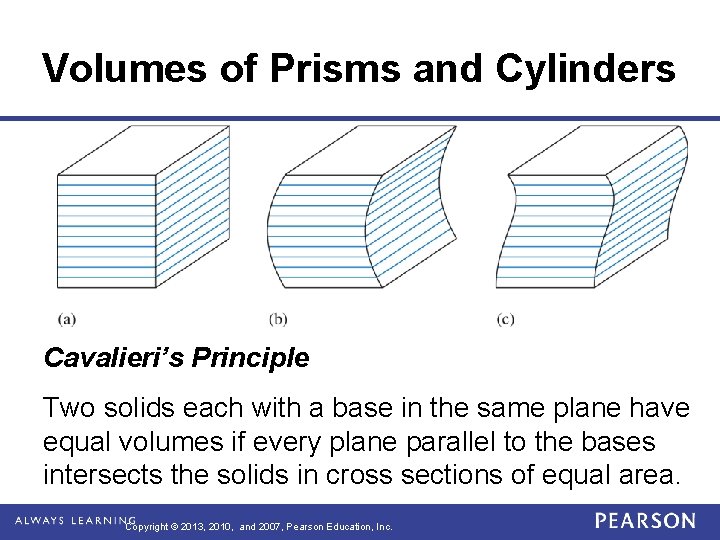
Volumes of Prisms and Cylinders Cavalieri’s Principle Two solids each with a base in the same plane have equal volumes if every plane parallel to the bases intersects the solids in cross sections of equal area. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -21 Find the volume of each figure. 216 cm 3 450 cm 3 Copyright © 2013, 2010, and 2007, Pearson Education, Inc. 250π cm 3

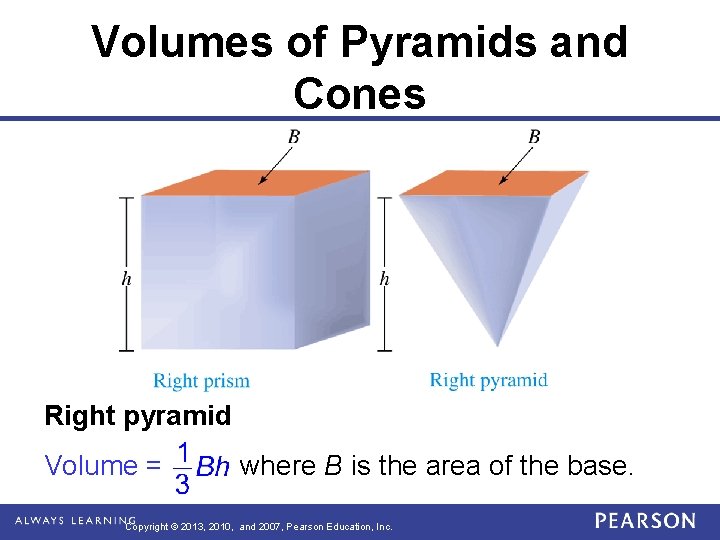
Volumes of Pyramids and Cones Right pyramid Volume = where B is the area of the base. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Volumes of Pyramids and Cones Right circular cone Volume = Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -22 Find the volume of each figure. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

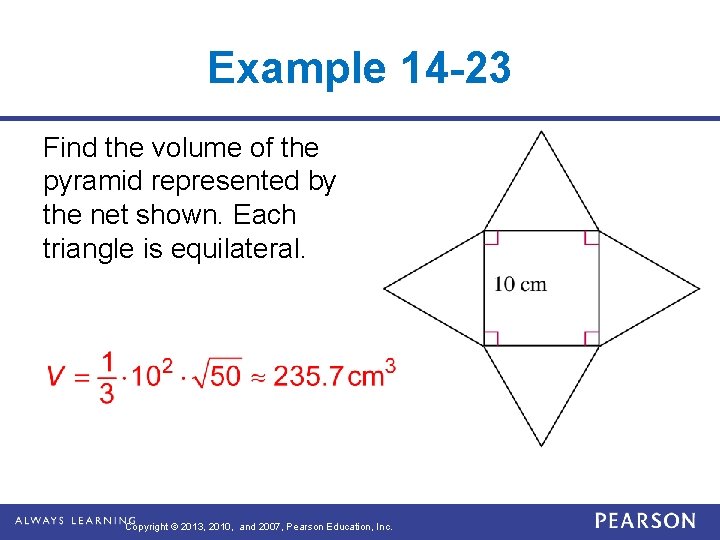
Example 14 -23 Find the volume of the pyramid represented by the net shown. Each triangle is equilateral. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

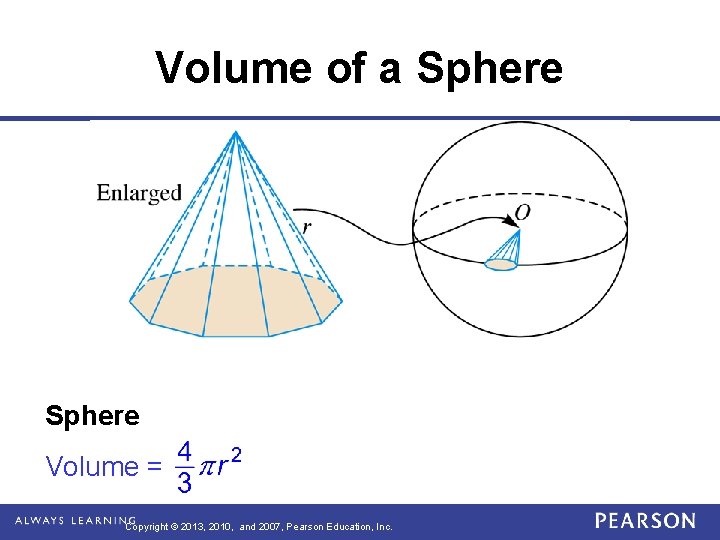
Volume of a Sphere Volume = Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -24 Find the volume of a sphere whose radius is 6 cm. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Comparing Measurements of Similar Figures Theorems The ratio of any linear measurement of two similar figures, for example, length, width, height, perimeter, diagonal, diameter, slant height, have the same scale factor k. For similar triangles with scale factor k, the ratio of their areas is k 2. For similar polygons with scale factor k, the ratio of their areas is k 2. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -25 Is it true that the viewing area of a 35 -inch television screen is about twice the viewing area of a 25 -inch television screen? Recall that television screens are measured diagonally. Areas of the ratios are: 352: 252 or 1225: 625 or 1. 96: 1 Therefore the viewing area of a 35 -inch screen is almost twice that of a 25 -inch screen. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Comparing Measurements of Similar Figures Theorems If the scale factor of two similar figures is k, then the scale factor of the areas or surface areas is k 2, and the ratio of volumes is k 3. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -26 a How does the surface area of a sphere 10 in. in diameter compare with the surface area of a sphere 5 in. in diameter? Any two spheres are similar. The ratios of the diameters is 10: 5 or 2. Ratio of surface areas is 22 or 4. The 10 -in sphere has 4 times the surface area of the 5 -inch sphere. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -26 b How does the volume of a sphere 10 in. in diameter compare with the volume of a sphere 5 in. in diameter? The ratios of the volumes is 23 or 8. The volume of a 10 -in sphere has 8 times the volume of the 5 -inch sphere. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Mass: a quantity of matter Weight: a force exerted by gravitational pull Gram: fundamental unit of mass in the metric system Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

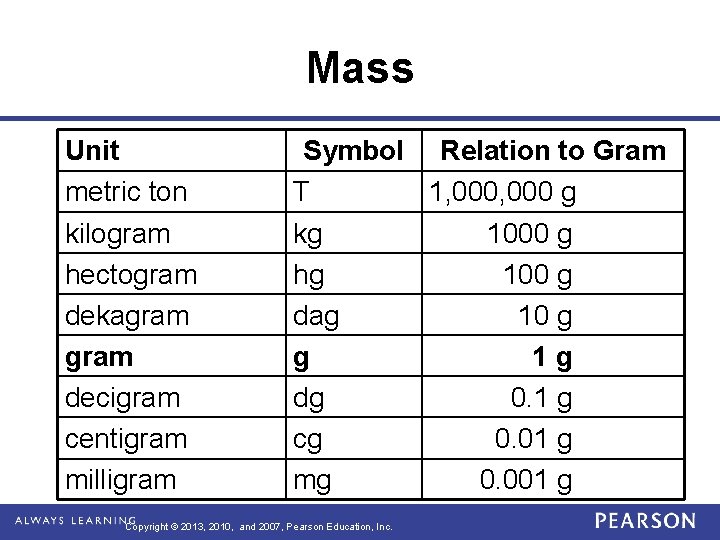
Mass Unit metric ton kilogram hectogram dekagram decigram centigram milligram Symbol Relation to Gram T 1, 000 g kg 1000 g hg 100 g dag 10 g g 1 g dg 0. 1 g cg 0. 01 g mg 0. 001 g Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -28 Convert each of the following: 0. 034 kg a. 34 g = _____ 6. 836 b. 6836 kg = _____ t Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

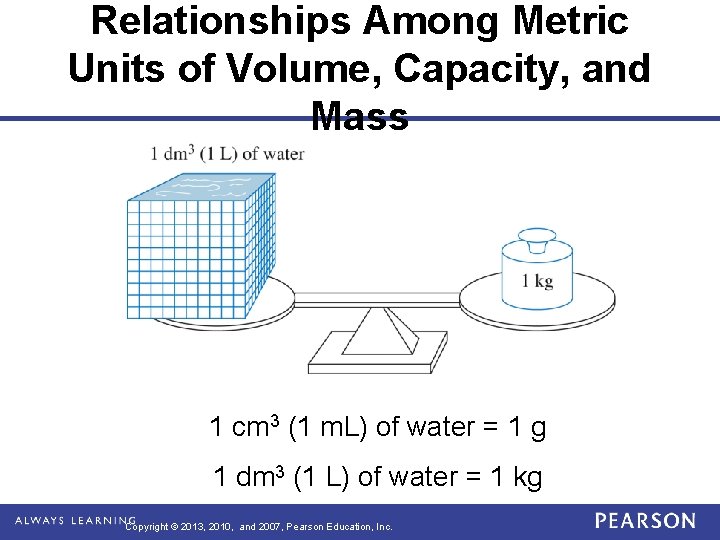
Relationships Among Metric Units of Volume, Capacity, and Mass 1 cm 3 (1 m. L) of water = 1 g 1 dm 3 (1 L) of water = 1 kg Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 14 -29 A waterbed measures 180 cm x 210 cm x 20 cm. a. Approximately how many liters of water can it hold? b. What is its mass in kilograms when it is full of water? Because 1 L of water has a mass of 1 kg, 756 L of water has a mass of 756 kg, which is 0. 756 t. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

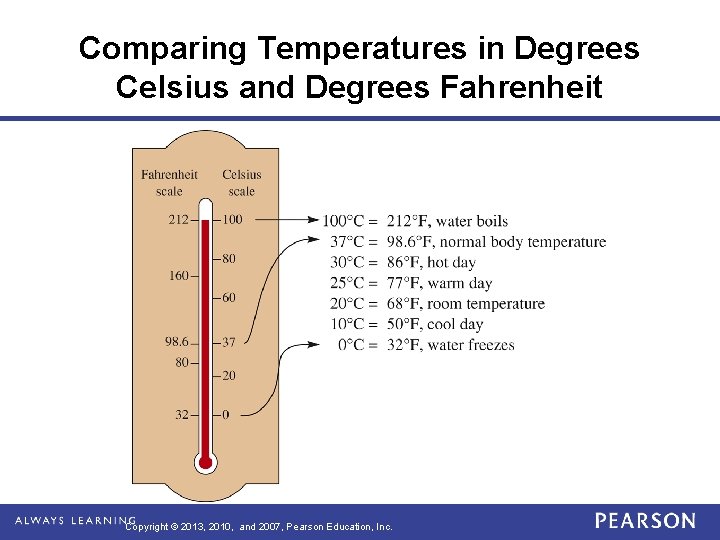
Temperature degree Kelvin: base unit of temperature in the metric system; used only for scientific measurements. The freezing point of water is 273°K. degree Celsius: used for customary temperature measurements in the metric system. Its scale has 100 equal divisions. The freezing point of water is 0°C, and its boiling point is 100°C. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Temperature degree Fahrenheit: used for customary temperature measurements in the English system. Its scale has 180 equal divisions. The freezing point of water is 32°F, and its boiling point is 212°F. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Comparing Temperatures in Degrees Celsius and Degrees Fahrenheit Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Converting between degrees Celsius and degrees Fahrenheit To convert temperatures, use the following formulas: Copyright © 2013, 2010, and 2007, Pearson Education, Inc.