Chapter 13 The Graph Abstract Data Type Data

Chapter 13: The Graph Abstract Data Type • Data Structures in Java: From Abstract Data Types to the Java Collections Framework • by Simon Gray Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Graph Terminology • A graph G = (V, E) is an ordered pair of finite sets V and E, where V(G) is the set of vertices in G, and E(G) is the set of edges in G. The edge connecting vertices vi and vj is represented as (vi , vj). The number of vertices in G is given as |V| and the number of edges in G is given as |E|. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 2

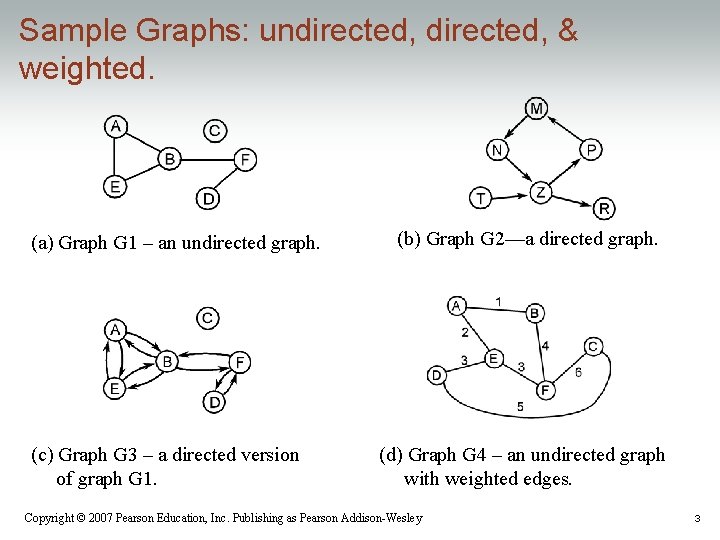
Sample Graphs: undirected, & weighted. (a) Graph G 1 – an undirected graph. (c) Graph G 3 – a directed version of graph G 1. (b) Graph G 2—a directed graph. (d) Graph G 4 – an undirected graph with weighted edges. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 3

Graph Terminology • • adjacency of vertices in-degree & out-degree weighted edges path, simple path & cycle connected & reachable connected graph complete graph subgraph Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 4

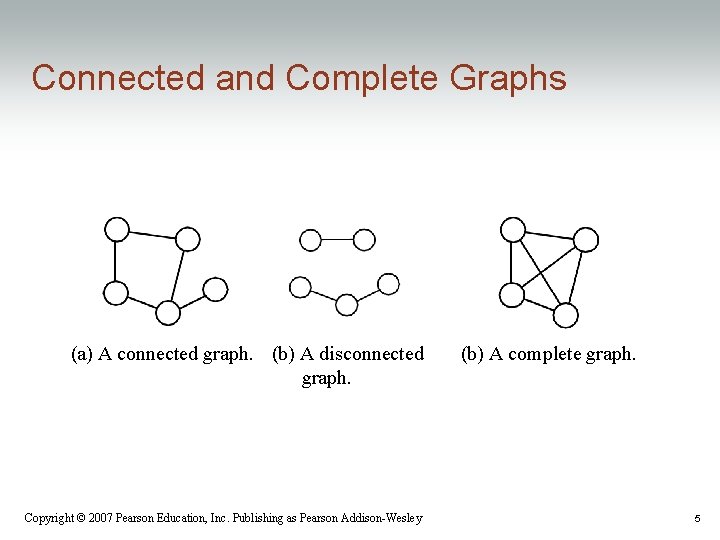
Connected and Complete Graphs (a) A connected graph. (b) A disconnected graph. Copyright ©

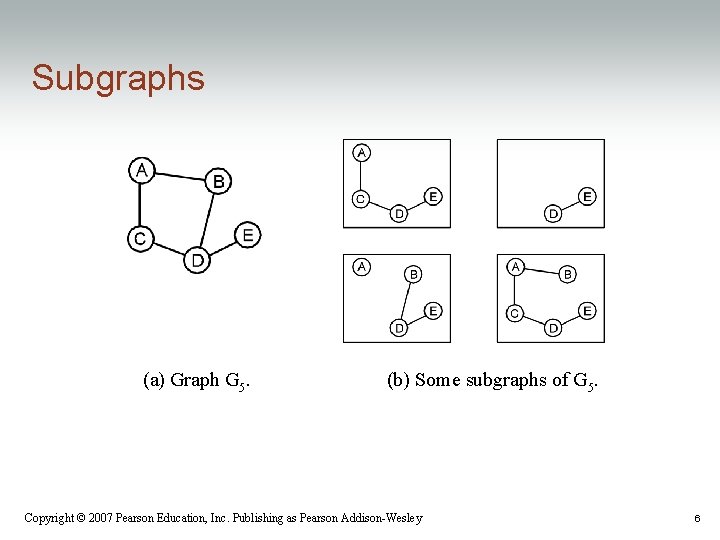
Subgraphs (a) Graph G 5. (b) Some subgraphs of G 5. Copyright © 2007

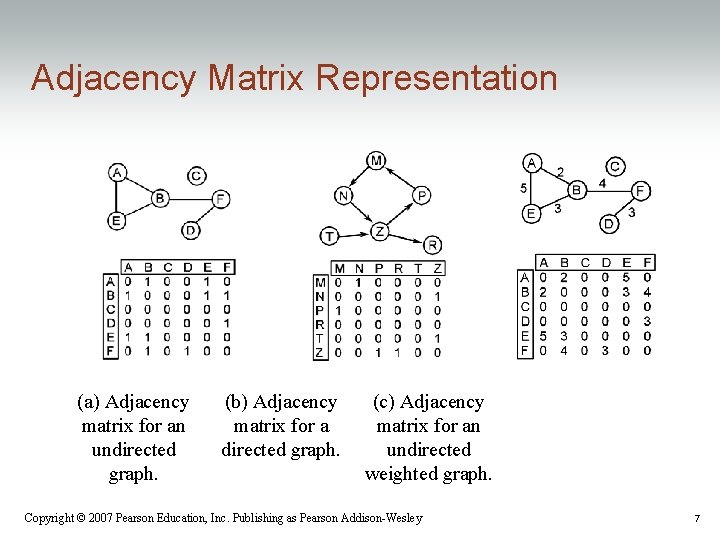
Adjacency Matrix Representation (a) Adjacency matrix for an undirected graph. (b) Adjacency matrix for a directed graph. (c) Adjacency matrix for an undirected weighted graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 7

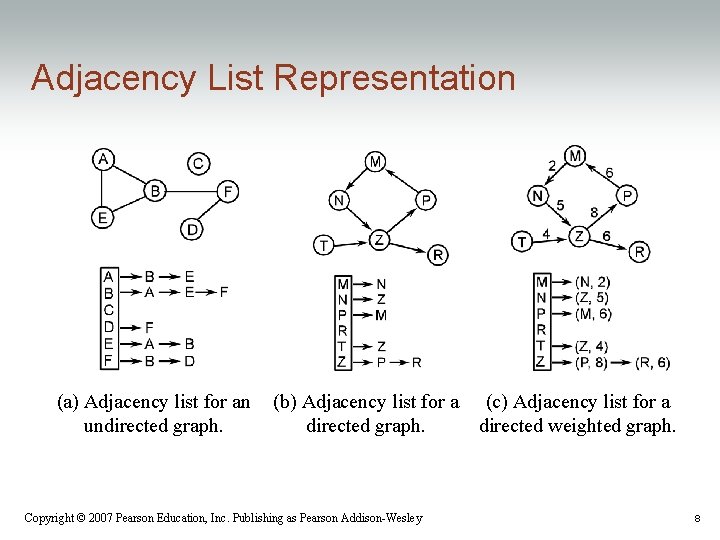
Adjacency List Representation (a) Adjacency list for an undirected graph. (b) Adjacency list for a directed graph. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley (c) Adjacency list for a directed weighted graph. 8

Depth First Search // Perform a depth first search of a Graph g // originating from Vertex v Pseudocode DFS ( Graph g, Vertex v ) 1. mark v as visited // visit a vertex only once! 2. for each Vertex w adjacent to v 3. if w has not been visited 4. DFS( w ) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 9

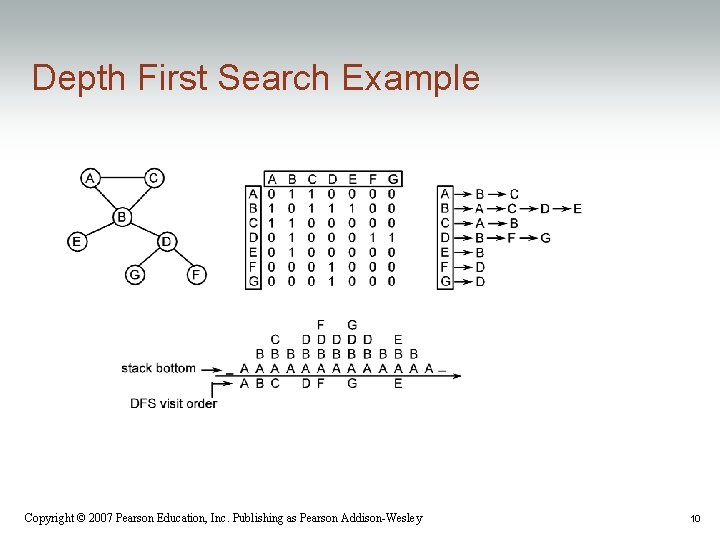
Depth First Search Example Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Breadth First Search // Perform a breadth first search of a Graph g // originating from Vertex v Pseudocode BFS ( Graph g, Vertex v ) vertex. Queue – a Queue of Vertices 1. mark v as visited 2. enqueue v in vertex. Queue 3. while vertex. Queue is not empty 4. let v be the element removed from the front of vertex. Queue 5. for all Vertices w adjacent to v 6. if w has not been visited 7. enqueue w in vertex. Queue 8. mark w as visited Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 11

Breadth First Search Example Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Shortest Path Algorithm List shortest. Path( Graph g, Vertex src, Vertex dest ) // Find a shortest path from src to dest in Graph g. Return an empty // List if no path // exists, or the vertices in the path from src to dest otherwise. If all edges have the same weight, then BFS will find shortest path. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13

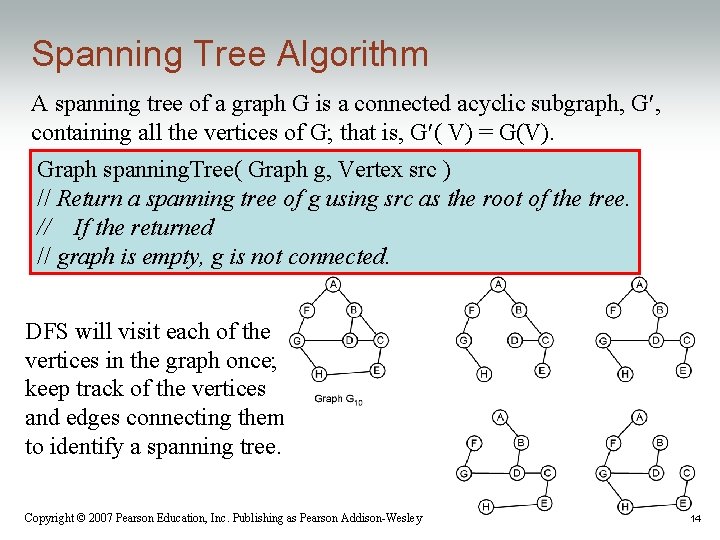
Spanning Tree Algorithm A spanning tree of a graph G is a connected acyclic subgraph, G , containing all the vertices of G; that is, G ( V) = G(V). Graph spanning. Tree( Graph g, Vertex src ) // Return a spanning tree of g using src as the root of the tree. // If the returned // graph is empty, g is not connected. DFS will visit each of the vertices in the graph once; keep track of the vertices and edges connecting them to identify a spanning tree. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 14

Minimal Path Algorithm // Return the cost of a minimal cost path in // Graph g from Vertex src to dest Pseudocode Minimal Path( Graph g, Vertex src, Vertex dest ) priority. Queue – a priority queue holding Vertex , min. Cost. To. Vertex pairs vertices. In. Some. Path. To. Dest – a collection of vertices in some possible path from src to dest 1. place src, 0 in priority. Queue 2. while priority. Queue is not empty // get the least expensive path seen so far 3. pair = the vertex, min. Cost. To. Vertex pair removed from priority. Queue 4. v = pair. vertex // extract the vertex field from pair 5. min. Cost. To. V = pair. min. Cost. To. Vertex // extract the cost field from pair 6. if v == dest 7. return min. Cost. To. V // success; return cost from src to v // haven’t found the target yet, so continue the search 8. add v to vertices. In. Some. Path. To. Dest 9. for each Vertex w adjacent to v 10. if w is not in vertices. In. Some. Path. To. Dest // avoid revisiting a visited vertex 11. let min. Cost. To. W be min. Cost. To. V + weight(v, w) // get total cost from src to w 12. add the pair w, min. Cost. To. W to priority. Queue 13. return failure // there is no path from src to dest Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 15

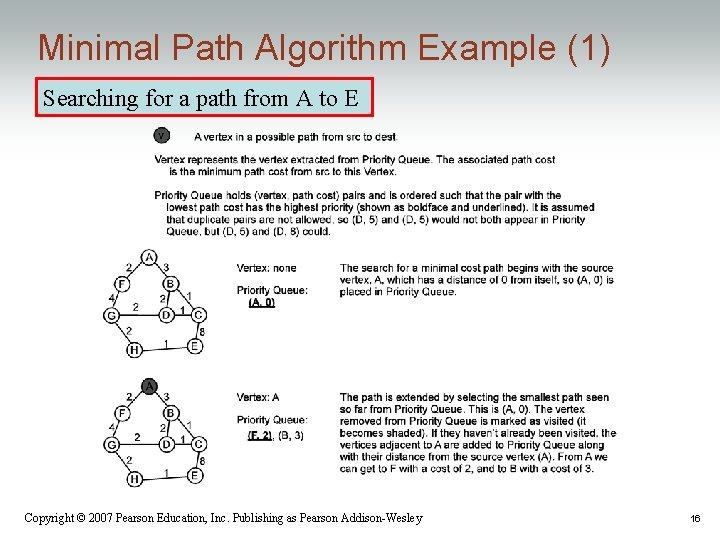
Minimal Path Algorithm Example (1) Searching for a path from A to E Copyright

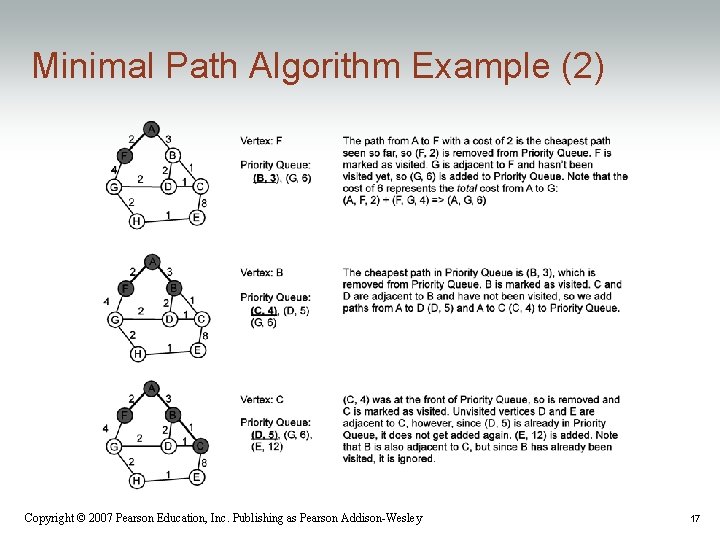
Minimal Path Algorithm Example (2) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

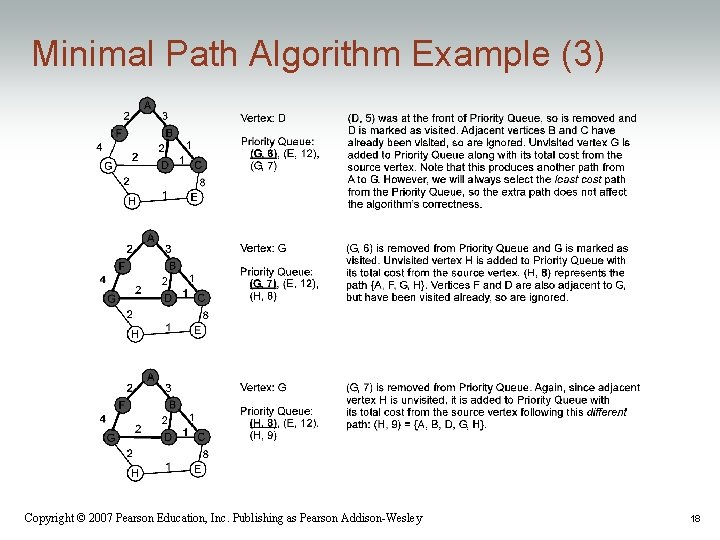
Minimal Path Algorithm Example (3) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

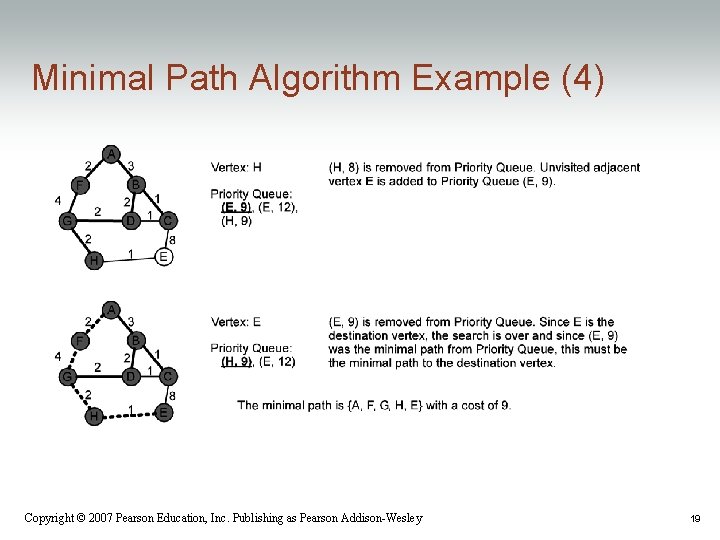
Minimal Path Algorithm Example (4) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

Minimal Spanning Tree Algorithm // Identify a Minimal Spanning Tree for a weighted Graph g with Vertex v as its root. Pseudocode minimal. Spanning. Tree ( Graph g, Vertex v ) MST – a collection of edges (v, w) in the Minimal Spanning Tree; initially this collection is empty mst. Cost – the total cost of all edges in MST; initially 0 visited. Vertices – a collection of all vertices that are in MST; initially this collection stores a vertex from G that will be the root of the MST 1. all. Vertices. Visited = false 2. put the starting vertex v in visited. Vertices // while the MST is not complete and there are vertices to visit 3. while MST. size() < |V| - 1 and not all. Vertices. Visited // select the least cost candidate edge 4. get the least cost edge (v, w) such that v is in visited. Vertices 5. and w is not in visited. Vertices 6. if no such edge exists then 7. all. Vertices. Visited is true 8. else 9. add (v, w) to MST 10. add the cost of edge (v, w) to mst. Cost 11. add w to visited. Vertices // loop invariant: MST contains the edges of a minimal spanning // tree for all vertices from G that are in visited. Vertices 12. if MST. size() != |V| - 1 then 13. return failure 14. return MST // success Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 20

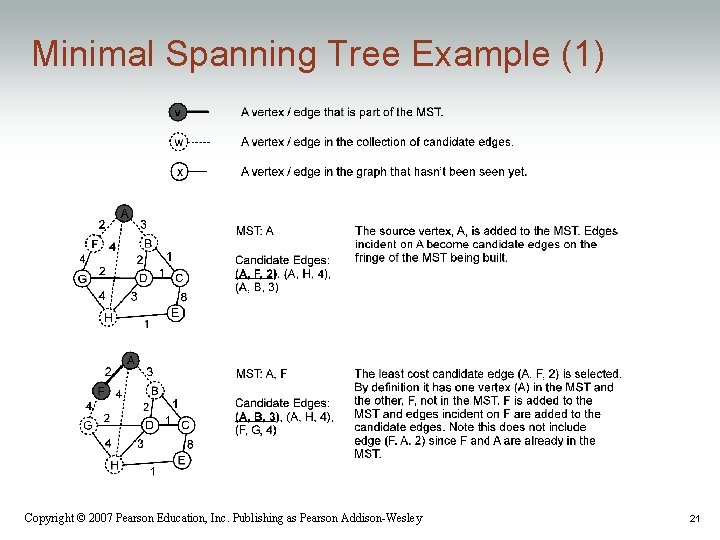
Minimal Spanning Tree Example (1) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

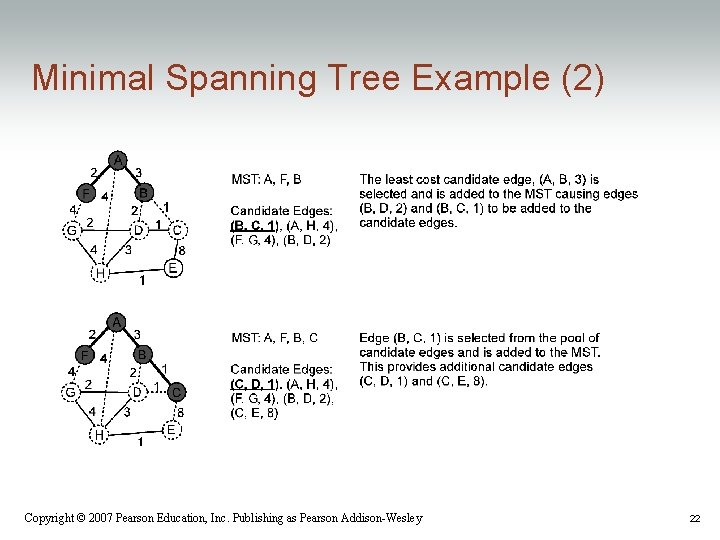
Minimal Spanning Tree Example (2) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

Minimal Spanning Tree Example (3) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

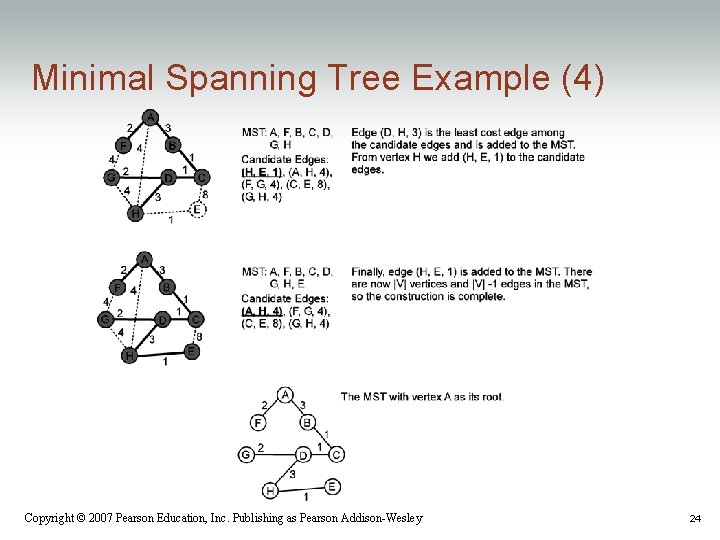
Minimal Spanning Tree Example (4) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson

The Graph ADTs • What needs to be explicitly represented in a graph? Do we need a type to represent vertices? What about edges? • Our solution: explicitly represent vertices and implicitly represent edges via the vertices they connect • Graph ADT 13. 1 specifies an unweighted graph that could be directed or undirected • Weighted Graph ADT 13. 2 is as an extension of the Graph ADT. The only significant difference is the addition of operations to support edge weights • This design decision will be reflected in the implementation Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 25

The Graph Implementation • Let the Graph interface reflect the Graph ADT • Questions: – Can a directed graph class and an undirected graph class be directly related? – Should a digraph be a subclass of an undirected graph class, or vice versa? – How do weighted graphs affect this design? Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 26

The Graph Implementation • How to handle the addition and deletion of edges? • The add. Edge(v 1, v 2) operation will produce an edge from v 1 to v 2 in a directed graph, and an edge from v 2 to v 1 in an undirected graph • Adj. Matrix. Di. Graph will implement the Graph interface for directed graphs using an adjacency matrix to store the graph • To represent undirected graphs, Adj. Matrix. Graph will be a subclass of Adj. Matrix. Di. Graph. When dealing with edges, its methods will invoke their superclass (directed graph) counterparts, and then will handle the bidirectionality of an undirected graph locally Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 27

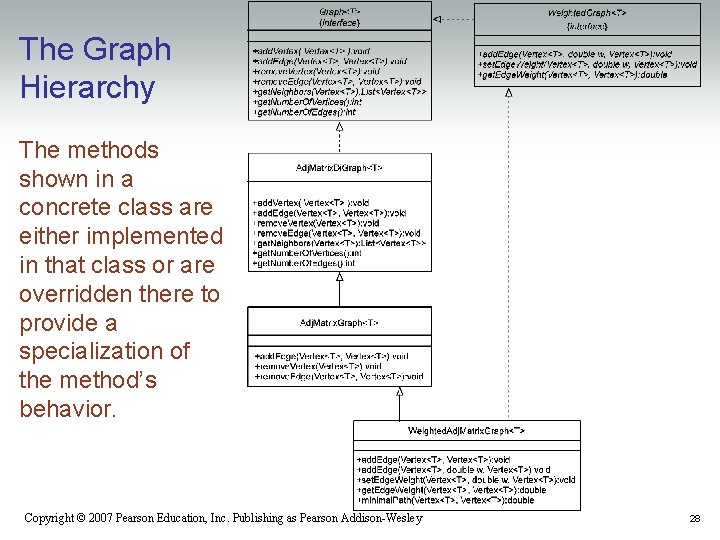
The Graph Hierarchy The methods shown in a concrete class are either implemented in that class or are overridden there to provide a specialization of the method’s behavior. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 28

Adj. Matrix. Di. Graph package gray. adts. graph; import java. util. *; /** * An implementation of the <tt>Graph</tt> interface for a * directed graph using an adjacency matrix to indicate the * presence/absence of edges connecting vertices in the graph. */ public class Adj. Matrix. Di. Graph<T> implements Graph<T> { protected protected int number. Of. Vertices; int number. Of. Edges; int[][] adj. Matrix; Vertex<T>[] vertices; int v 1 Pos, v 2 Pos; static int SIZE = 10; Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Note the use of protected here so subclasses can have direct access. 29

Method add. Edge() // directed graph! public void add. Edge( Vertex<T> v 1, Vertex<T> v 2 ) { v 1 Pos = get. Vertices. Index. For( v 1 ); v 2 Pos = get. Vertices. Index. For( v 2 ); if ( v 1 Pos == -1 || v 2 Pos == -1 ) { throw new Illegal. Argument. Exception( "vertex not found" ); } // avoid adding duplicate edges if ( this. adj. Matrix[v 1 Pos][v 2 Pos] == 0 ) { this. adj. Matrix[v 1 Pos][v 2 Pos] = 1; this. number. Of. Edges++; } else { throw new Illegal. Argument. Exception( "duplicate edge " + v 1 + " " + v 2 ); } } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 30

Method add. Edge() // undirected graph! /** * Adjacency Matrix implementation of an undirected * Graph. */ public class Adj. Matrix. Graph<T> extends Adj. Matrix. Di. Graph<T> { public Adj. Matrix. Graph() { let superclass create the super(); } edge from v 1 to v 2 public void add. Edge( Vertex<T> v 1, Vertex<T> v 2 ) { super. add. Edge( v 1, v 2 ); } // if we get here, the superclass method completed // successfully and we can set edge from v 2 to v 1 this. adj. Matrix[v 2 Pos][v 1 Pos] = 1; now create the Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley v 2 to v 1 edge 31

Weighted. Adj. Matrix. Graph /** * A weighted, undirected graph stored in an adjacency * matrix. The weights must be >= 0. */ public class Weighted. Adj. Matrix. Graph<T> extends Adj. Matrix. Graph<T> implements Weighted. Graph<T> { /** * The default weight for an edge in a weighted graph. */ public double DEFAULT_WEIGHT = 1. 0; /** * Store weight edges. The adjacency matrix storing * edges is in an ancestor class. */ protected double[][] weights; Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 32

add. Edge() // weighted undirected graph! public void add. Edge( Vertex<T> v 1, double weight, Vertex<T> v 2 ) { if ( weight < 0. 0 ) { throw new Illegal. Argument. Exception( "Edge weight " + " must be >= 0. 0" ); } super. add. Edge( v 1, v 2 ); // if we get here, method in superclass didn't throw // an exception and method preconditions are met this. set. Edge. Weight( v 1, weight, v 2 ); } Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 33

overridden add. Edge() Overridden add. Edge() inherited from Adj. Matrix. Graph. Need to provide a weight for the edge; use the default value. public void add. Edge( Vertex<T> v 1, Vertex<T> v 2 ) { this. add. Edge( v 1, DEFAULT_WEIGHT, v 2 ); } More code reuse: Use the add. Edge() from the previous slide and just supply a DEFAULT_WEIGHT. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 34