Chapter 13 String Matching Data Structures and Algorithms

Chapter 13 String Matching Data Structures and Algorithms in Java

Objectives Discuss the following topics: • Exact String Matching • Approximate String Matching • Case Study: Longest Common Substring Data Structures and Algorithms in Java 2

Exact String Matching • Stringology’s major area of interest is pattern matching • Exact string matching consists of finding an exact copy of pattern P in text T Data Structures and Algorithms in Java 3

Exact String Matching (continued) brute. Force. String. Matching(pattern P, text T) i = 0; while i ≤ |T| - |P| j = 0; while Ti == Pj and j < |P| i++; // try to match all characters in P; j++; if j == |P| return match at i - |P|; // success if the end of P is reached; // if there is a mismatch, i = i - j + 1; // shift P to the right by one position; return no match; // failure if fewer characters left in T than |P|; Data Structures and Algorithms in Java 4

Exact String Matching (continued) Hancart(pattern P, text T) if P 0 == P 1 s. Equal = 1; s. Diff = 2; else s. Equal = 2; s. Diff = 1; i = 0; while i ≤ |T| - |P| if Ti+1 ≠ P 1 i = i + s. Diff; else j = 1; while j < |P| and Ti+j == Pj j++; if j == |P| and P 0 == Ti return match at i; i = i + s. Equal; return no match; Data Structures and Algorithms in Java 5

The Knuth-Morris-Pratt Algorithm The Knuth-Morris-Pratt algorithm can be obtained from brute. Force. String. Matching() Knuth. Morris. Pratt(pattern P, text T) find. Next (P, next) i = j = 0; while i ≤ |T| - |P| while j == -1 or j < |P| and Ti == Pj i++; //increment i only for matched character; j++; if j == |P| return a match at i - |P|; j = next |j| //in the case of a mismatch, i does not change; return no match; Data Structures and Algorithms in Java 6

The Boyer-Moore Algorithm The Boyer-Moore algorithm tries to match P with T by comparing them from right to left, not from left to right Data Structures and Algorithms in Java 7

The Boyer-Moore Algorithm (continued) Boyer. Moore. Simple(pattern P, text T) initialize all cells of delta 1 to |P| for j = 0 to |P| - 1 delta 1[Pj] = |P| - j – 1; i = |P| - 1; while i < |T| j = |P| - 1; while j ≥ 0 and Pj == Ti i --; j --; if j == -1 return match at i+1; i = i + max(delta 1| Ti |, |P|-j); return no match; Data Structures and Algorithms in Java 8

The Sunday Algorithms • Daniel Sunday (1990) observed that in the case of a mismatch with a text character Ti, the pattern shifts to the right by at least one position; thus, the character Ti+|P| is included • More advantageous to build delta 1 with respect to character Ti+|P| • Sunday introduced two more algorithms, based on a generalized delta 2 table Data Structures and Algorithms in Java 9

Multiple Searches • All preceding algorithms presented find an occurrence of a pattern in text and discontinue after finding the first. • Modifying the Boyer-Moore algorithm allows for multiple searches Data Structures and Algorithms in Java 10

Multiple Searches (continued) Boyer. Moore. Simple(pattern P, text T) initialize all cells of delta 1 to |P| for j = 0 to |P| - 1 delta 1[Pj] = |P| - j – 1; compute delta 2; i = |P| - 1; while i < |T| j = |P| - 1; while j ≥ 0 and Pj == Ti i --; j --; if j == -1 output match at i+1; i = i + |P| + 1; //shift P by one position to the right else i = i + max(delta 1 [Ti], delta 2[j]); Data Structures and Algorithms in Java 11

Bit-Oriented Approach • Each state of the search is represented as a number—that is, a string of bits—and a transition from one state to the next is the result of a small number of bitwise operations • A shift-and algorithm that uses a bit-oriented approach for string matching was proposed by Baeza-Yates and Gonnet (1992) Data Structures and Algorithms in Java 12

Matching Sets of Words • To considerably improve run time by considering all relevant words at the same time during the match process, Aho and Corasick (1975) constructed a string-match automation algorithm • The goto function is constructed in the form of a trie, or multiway tree, in which consecutive characters of a string are used to navigate the search in the tree Data Structures and Algorithms in Java 13

Matching Sets of Words (continued) Aho. Corasick(set keywords, text T) compute. Goto. Function(keywords, g, output); // the output function is computed compute. Failure. Function(g, output, f); // in these two functions; state = 0; for i = 0 to |T| - 1 while g(state, Ti) == fail state = f(state); state = g(state, Ti); if output(state) is not empty output: a match ending at i; output(state); Data Structures and Algorithms in Java 14

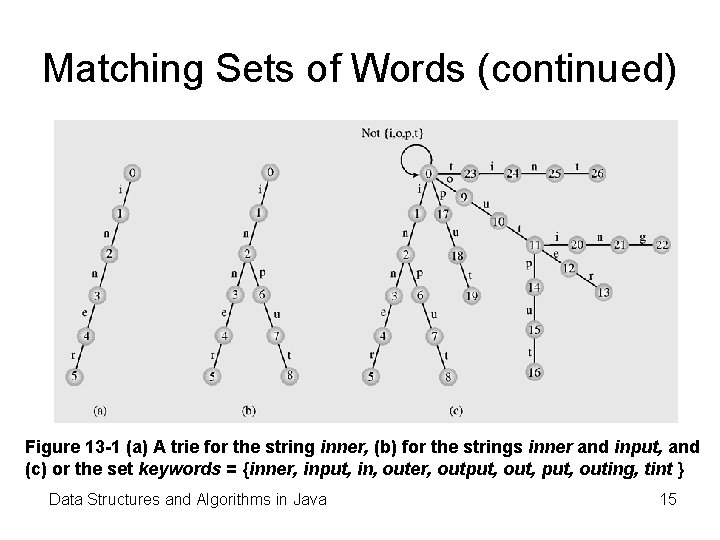
Matching Sets of Words (continued) Figure 13 -1 (a) A trie for the string inner, (b) for the strings inner and input, and (c) or the set keywords = {inner, input, in, outer, output, out, put, outing, tint } Data Structures and Algorithms in Java 15

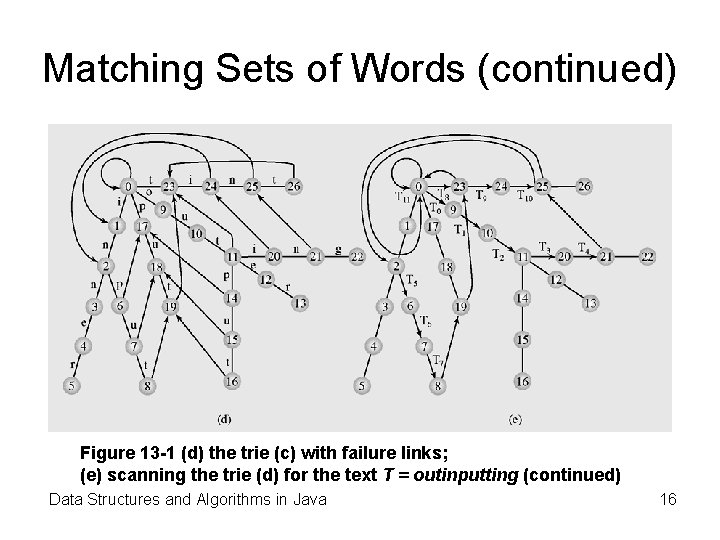
Matching Sets of Words (continued) Figure 13 -1 (d) the trie (c) with failure links; (e) scanning the trie (d) for the text T = outinputting (continued) Data Structures and Algorithms in Java 16

Regular Expression Matching • All letters of the alphabet are regular expressions • If r and s are regular expressions, then r|s, (r), r*, and rs are regular expressions. – Regular expression r|s represents regular expression r or s – Regular expression r* (where the star is called a Kleene closure) represents any finite sequence of rs: r, rrr, . . Data Structures and Algorithms in Java 17

Regular Expression Matching (continued) – Regular expression rs represents a concatenation rs – (r) represents regular expression r Data Structures and Algorithms in Java 18

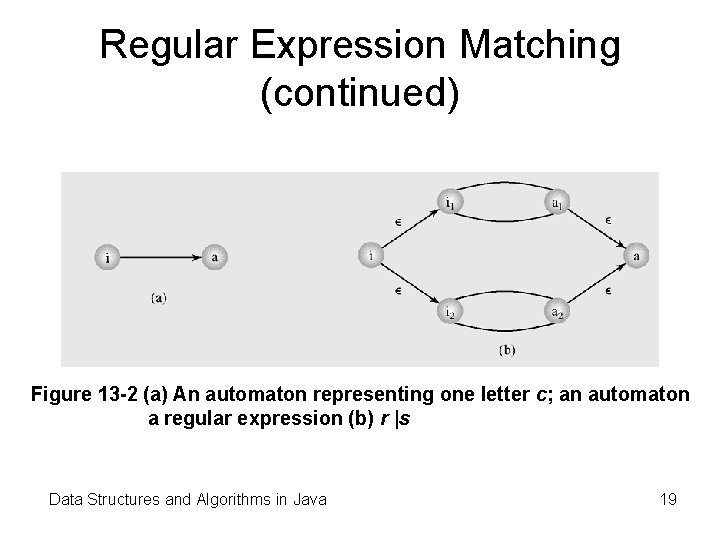
Regular Expression Matching (continued) Figure 13 -2 (a) An automaton representing one letter c; an automaton a regular expression (b) r |s Data Structures and Algorithms in Java 19

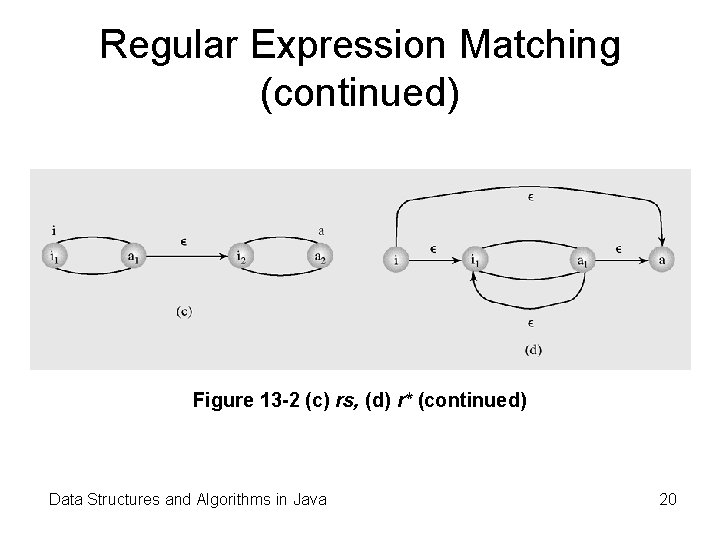
Regular Expression Matching (continued) Figure 13 -2 (c) rs, (d) r* (continued) Data Structures and Algorithms in Java 20

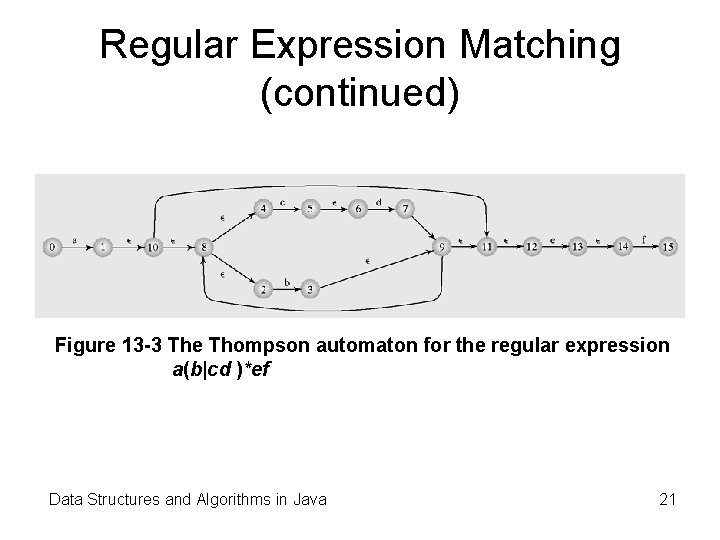
Regular Expression Matching (continued) Figure 13 -3 The Thompson automaton for the regular expression a(b|cd )*ef Data Structures and Algorithms in Java 21

Suffix Tries and Trees • A suffix trie for a text T is a tree structure in which each edge is labeled with one letter of T and each suffix of T is represented in the trie as a concatenation of edge labels from the root to some node of the trie Data Structures and Algorithms in Java 22

Suffix Tries and Trees (continued) Figure 13 -4 (a) A suffix trie for the string caracas Data Structures and Algorithms in Java 23

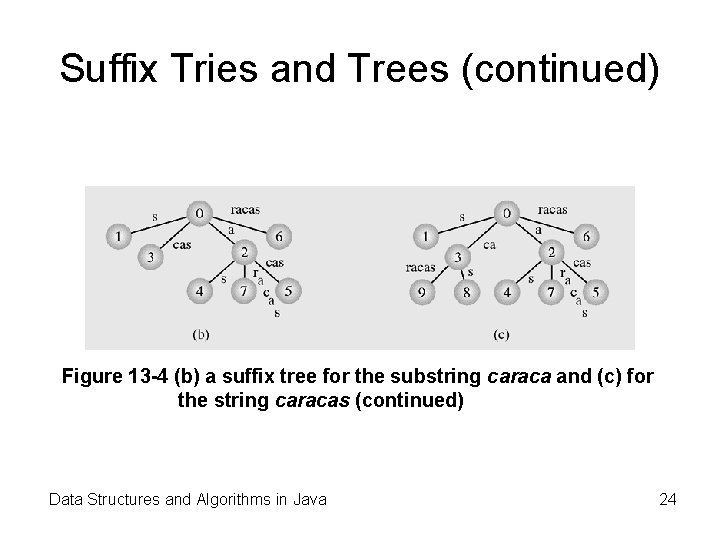
Suffix Tries and Trees (continued) Figure 13 -4 (b) a suffix tree for the substring caraca and (c) for the string caracas (continued) Data Structures and Algorithms in Java 24

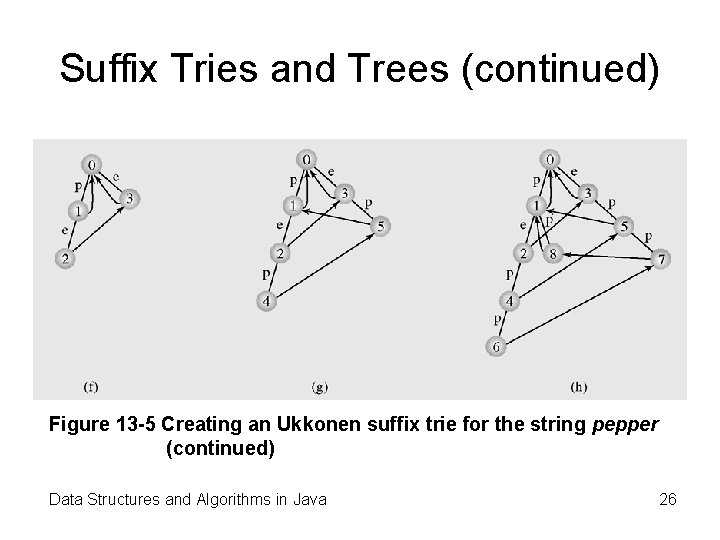
Suffix Tries and Trees (continued) Figure 13 -5 Creating an Ukkonen suffix trie for the string pepper Data Structures and Algorithms in Java 25

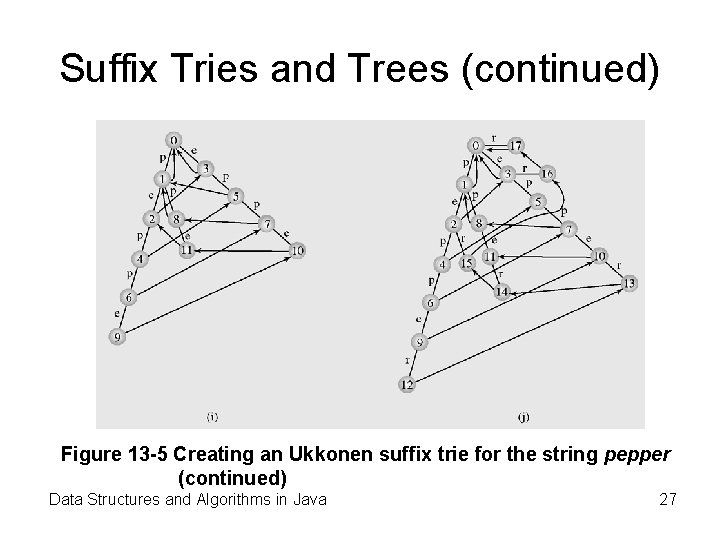
Suffix Tries and Trees (continued) Figure 13 -5 Creating an Ukkonen suffix trie for the string pepper (continued) Data Structures and Algorithms in Java 26

Suffix Tries and Trees (continued) Figure 13 -5 Creating an Ukkonen suffix trie for the string pepper (continued) Data Structures and Algorithms in Java 27

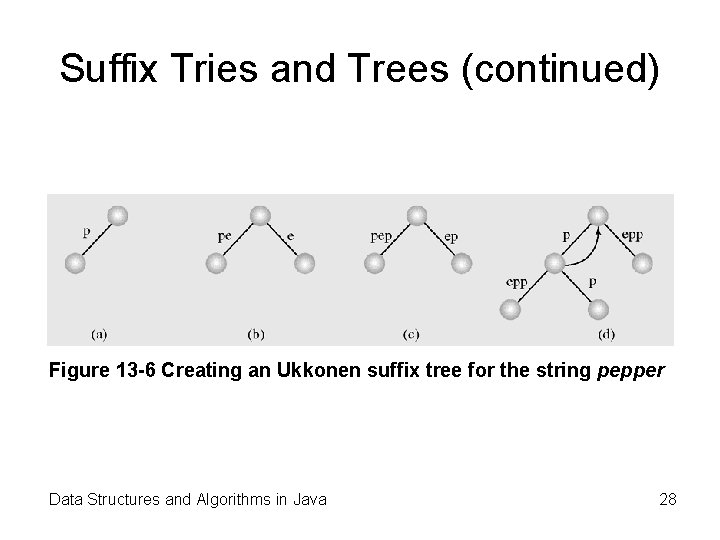
Suffix Tries and Trees (continued) Figure 13 -6 Creating an Ukkonen suffix tree for the string pepper Data Structures and Algorithms in Java 28

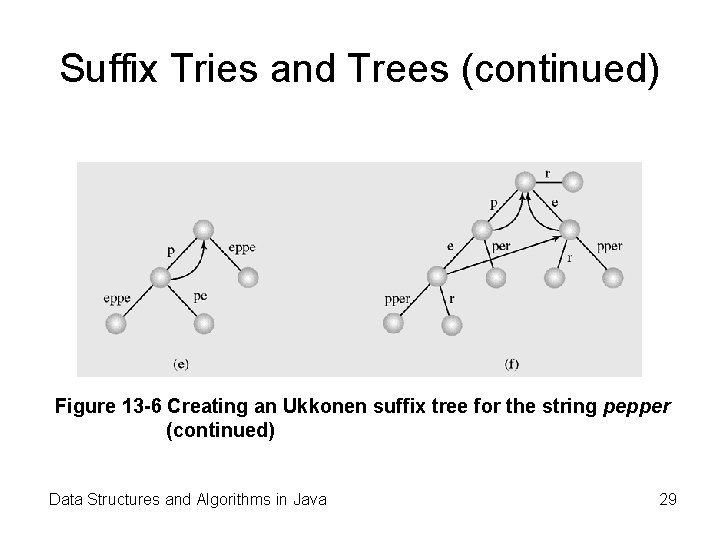
Suffix Tries and Trees (continued) Figure 13 -6 Creating an Ukkonen suffix tree for the string pepper (continued) Data Structures and Algorithms in Java 29

Suffix Arrays • If suffix trees require too much space, a simple alternative are suffix arrays (Manber and Myers, 1993) • Suffix array pos is the array position o through |T| - 1 of suffixes taken in lexicographic order • The Suffix array can be created from an existing suffix tree on which ordered depth-first traversal is performed Data Structures and Algorithms in Java 30

Approximate String Matching • A popular measure of the similarity of two strings is the number of elementary edit operations that are needed to transform one string into another • The differences between two strings is sought in terms of insertion (I), deletion (D), and substitution (S) • Difference can be represented in: trace, alignment (matching), and listing (derivation) Data Structures and Algorithms in Java 31

String Similarity • The string similarity problem can be approached by reducing the problem of finding the minimum distance for a particulate i and j to the problem of finding the minimum distance for values not larger than i and j • There are four possibilities: deletion, insertion, substitution, and match • The Wagner and Fischer algorithm (1974) attempts to address string similarity Data Structures and Algorithms in Java 32

String Matching with k Errors • To determine all substrings of text T for which the Levenshtein distance does not exceed k, perform string matching with k errors or k differences • All the possibilities for matching P(0…j) with a substring of T that ends at position i with e ≤ k errors can be summarized using Match, Substitution, Insertion, and Deletion where there is a match with e errors between P(0…j - 1) and a substring ending at Tj-1 Data Structures and Algorithms in Java 33

Case Study: Longest Common Substring Figure 13 -7 (a–h) Creating an Ukkonen suffix tree for the string abaabaac Data Structures and Algorithms in Java 34

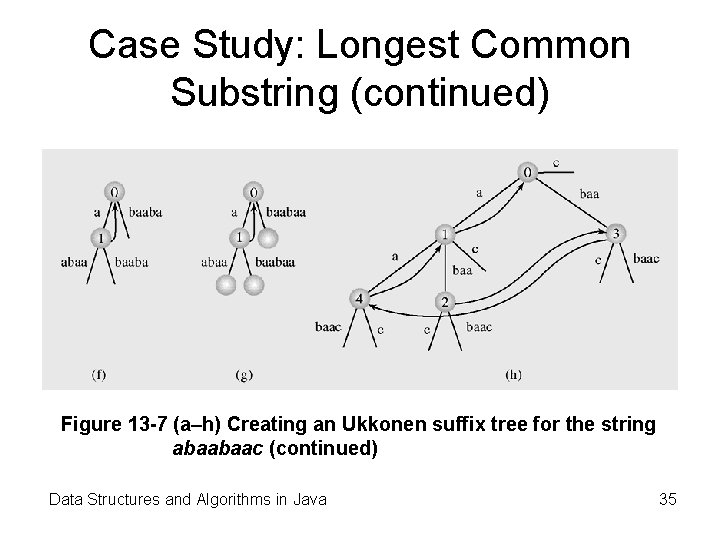
Case Study: Longest Common Substring (continued) Figure 13 -7 (a–h) Creating an Ukkonen suffix tree for the string abaabaac (continued) Data Structures and Algorithms in Java 35

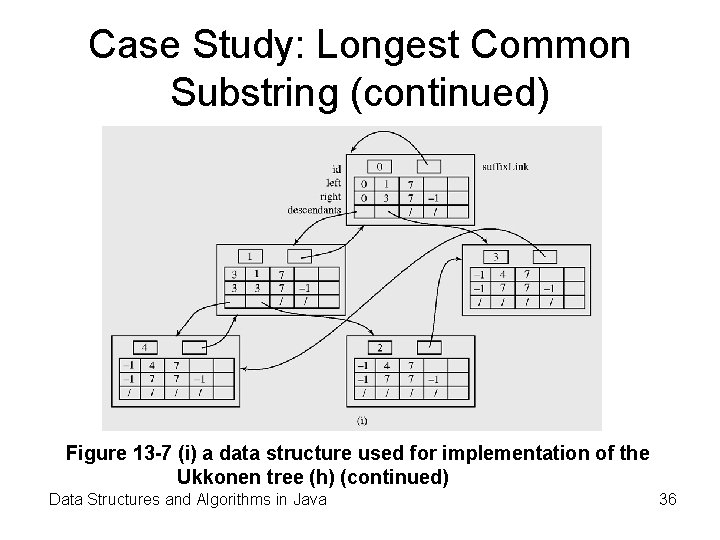
Case Study: Longest Common Substring (continued) Figure 13 -7 (i) a data structure used for implementation of the Ukkonen tree (h) (continued) Data Structures and Algorithms in Java 36

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring Data Structures and Algorithms in Java 37

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 38

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 39

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 40

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 41

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 42

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 43

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 44

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 45

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 46

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 47

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 48

Case Study: Longest Common Substring (continued) Figure 13 -8 Listing of the program to find longest common substring (continued) Data Structures and Algorithms in Java 49

Summary • Stringology’s major area of interest is pattern matching • Exact string matching consists of finding an exact copy of pattern P in text T • The brute. Force. String. Matching algorithm is an example of exact string matching • The Knuth-Morris-Pratt algorithm can be obtained from brute. Force. String. Matching() • The Boyer-Moore algorthm tries to match P with T by comparing them from right to left, not from left to right Data Structures and Algorithms in Java 50

Summary (continued) • Daniel Sunday (1990) observed that in the case of a mismatch with a text character Ti, the pattern shifts to the right by at least one position; thus, the character Ti+|P| is included. • Modifying the Boyer-Moore algorithm allows for multiple searches • A shift-and algorithm that uses a bit-oriented approach for string matching was proposed by Baeza-Yates and Gonnet (1992) • To considerably improve run time by considering all relevant word at the same time during the match process, Aho and Corasick (1975) constructed a string-match automation algorithm Data Structures and Algorithms in Java 51

Summary (continued) • All letters of the alphabet are regular expressions • A suffix trie for a text T is a tree structure in which each edge is labeled with one letter of T and each suffix of T is represented in the trie as a concatenation of edge labels from the root to some node of the trie • If suffix trees require too much space, a simple alternative are suffix arrays (Manber and Myers, 1993) Data Structures and Algorithms in Java 52

Summary (continued) • A popular measure of the similarity of two strings is the number of elementary edit operations that are needed to transform one string into another • The differences between two strings is sought in terms of insertion (I), deletion (D), and substitution (S) • The string similarity problem can be approached by reducing the problem of finding the minimum distance for a particulate i and j to the problem of finding the minimum distance for values not larger than i and j Data Structures and Algorithms in Java 53

Summary (continued) • The Wagner and Fischer algorithm (1974) attempts to address string similarity • To determine all substrings of text T for which the Levenshtein distance does not exceed k, perform string matching with k errors or k differences Data Structures and Algorithms in Java 54