CHAPTER 13 SIMPLE LINEAR REGRESSION Prem Mann Introductory














































- Slides: 71

CHAPTER 13 SIMPLE LINEAR REGRESSION Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

SIMPLE LINEAR REGRESSION MODEL Simple Regression p Linear Regression p Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Simple Regression Definition A regression model is a mathematical equation that describes the relationship between two or more variables. A simple regression model includes only two variables: one independent and one dependent. The dependent variable is the one being explained, and the independent variable is the one used to explain the variation in the dependent variable. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Linear Regression Definition A (simple) regression model that gives a straight-line relationship between two variables is called a linear regression model. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

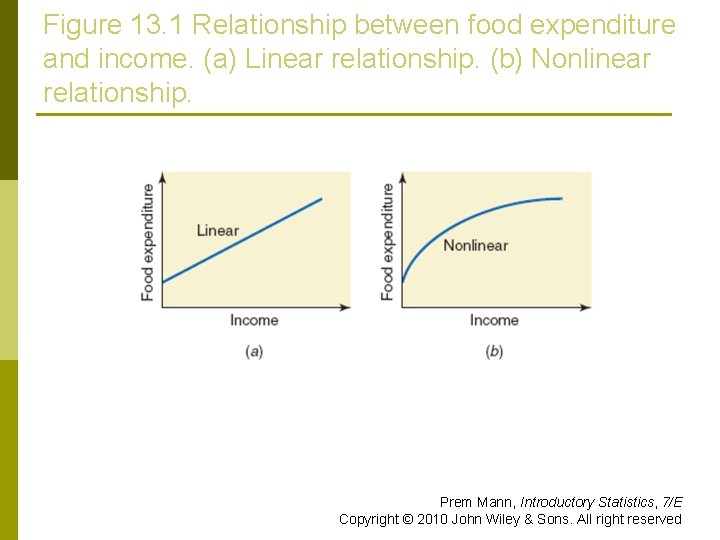
Figure 13. 1 Relationship between food expenditure and income. (a) Linear relationship. (b) Nonlinear relationship. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

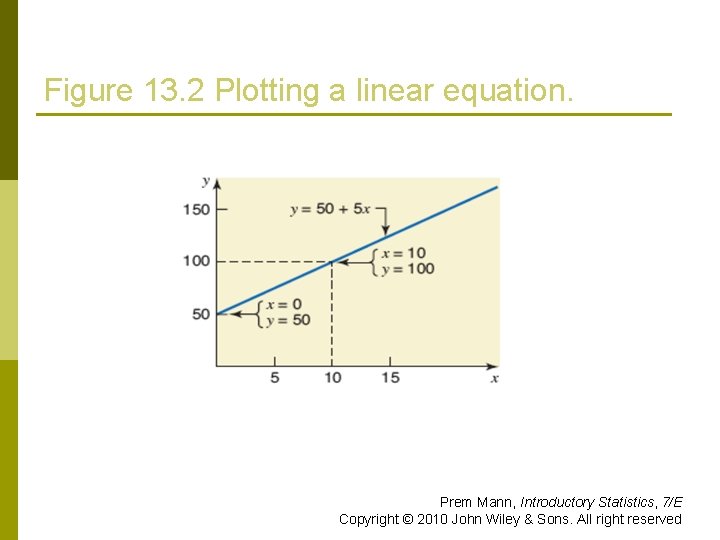
Figure 13. 2 Plotting a linear equation. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

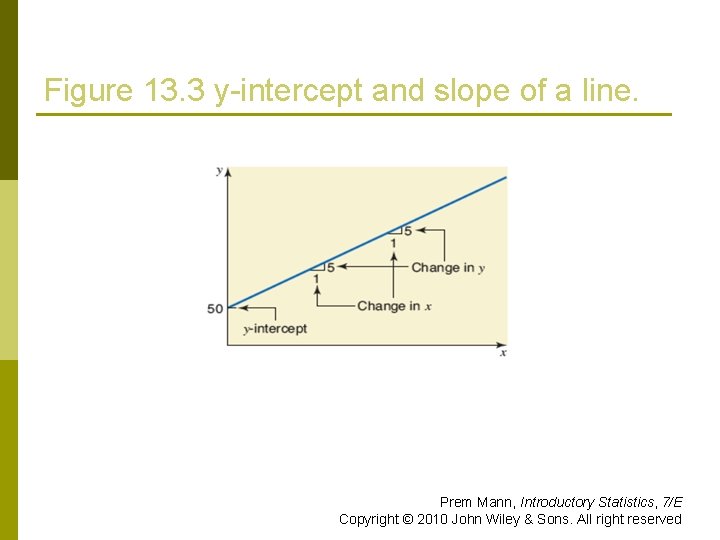
Figure 13. 3 y-intercept and slope of a line. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

SIMPLE LINEAR REGRESSION ANALYSIS Scatter Diagram p Least Squares Line p Interpretation of a and b p Assumptions of the Regression Model p Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

SIMPLE LINEAR REGRESSION ANALYSIS Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

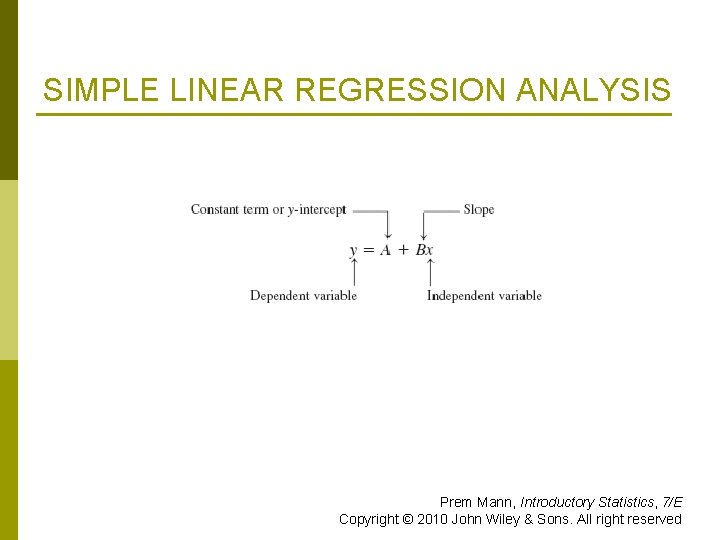
SIMPLE LINEAR REGRESSION ANALYSIS Definition In the regression model y = A + Bx + ε, A is called the y-intercept or constant term, B is the slope, and ε is the random error term. The dependent and independent variables are y and x, respectively. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

SIMPLE LINEAR REGRESSION ANALYSIS Definition In the model ŷ = a + bx, a and b, which are calculated using sample data, are called the estimates of A and B, respectively. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Table 13. 1 Incomes (in hundreds of dollars) and Food Expenditures of Seven Households Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Scatter Diagram Definition A plot of paired observations is called a scatter diagram. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

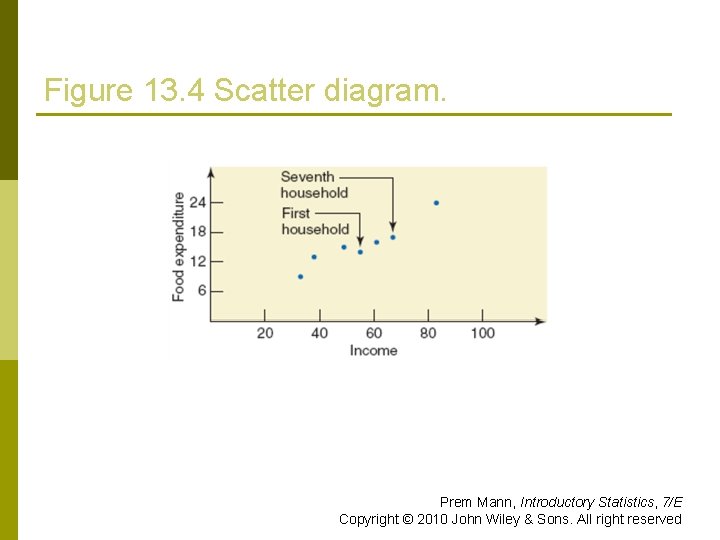
Figure 13. 4 Scatter diagram. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

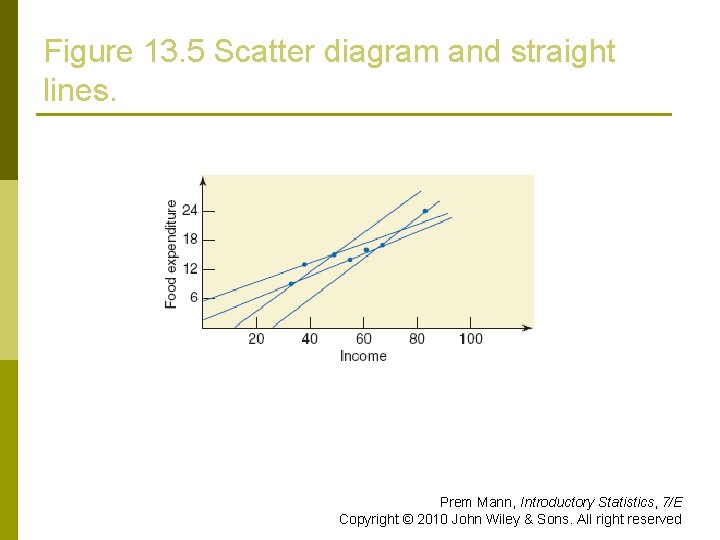
Figure 13. 5 Scatter diagram and straight lines. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

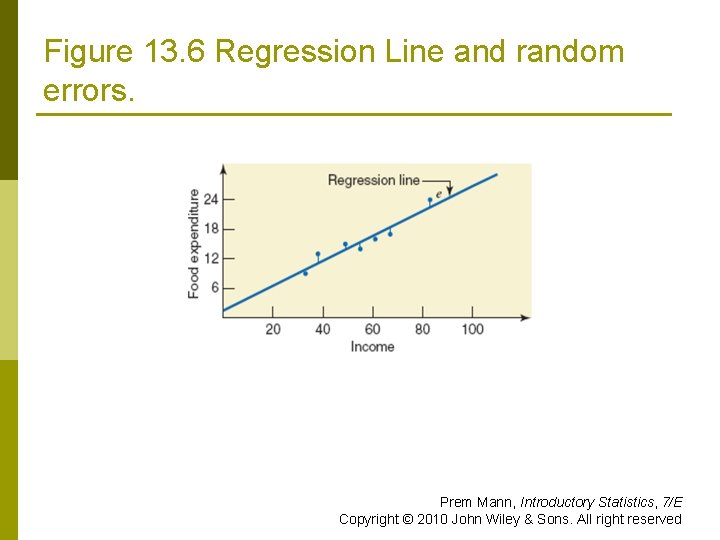
Figure 13. 6 Regression Line and random errors. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Error Sum of Squares (SSE) The error sum of squares, denoted SSE, is The values of a and b that give the minimum SSE are called the least square estimates of A and B, and the regression line obtained with these estimates is called the least square line. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

The Least Squares Line For the least squares regression line ŷ = a + bx, Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

The Least Squares Line where and SS stands for “sum of squares”. The least squares regression line ŷ = a + bx us also called the regression of y on x. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

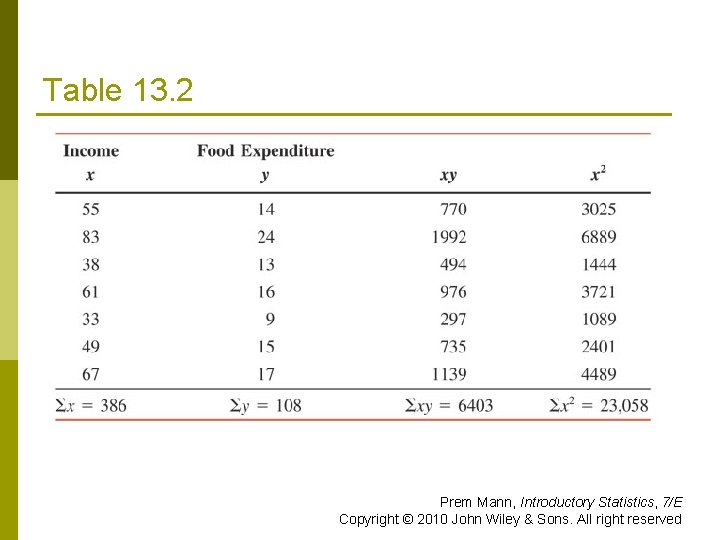
Example 13 -1 Find the least squares regression line for the data on incomes and food expenditure on the seven households given in the Table 13. 1. Use income as an independent variable and food expenditure as a dependent variable. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Table 13. 2 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -1: Solution Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -1: Solution Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

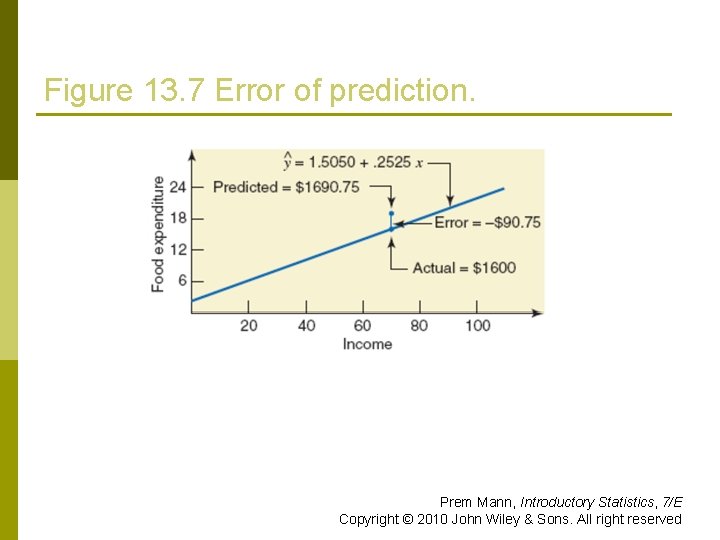
Example 13 -1: Solution Thus, our estimated regression model is ŷ = 1. 5050 +. 2525 x Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Figure 13. 7 Error of prediction. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Interpretation of a and b Interpretation of a p Consider the household with zero income. Using the estimated regression line obtained in Example 13 -1, n ŷ = 1. 5050 +. 2525(0) = $1. 5050 hundred Thus, we can state that households with no income is expected to spend $150. 50 per month on food p The regression line is valid only for the values of x between 33 and 83 p Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

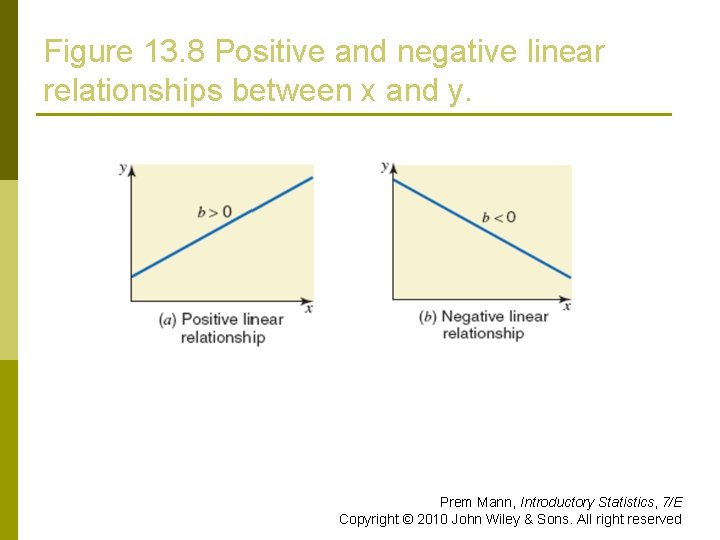
Interpretation of a and b Interpretation of b p The value of b in the regression model gives the change in y (dependent variable) due to change of one unit in x (independent variable). p We can state that, on average, a $100 (or $1) increase in income of a household will increase the food expenditure by $25. 25 (or $. 2525). Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Figure 13. 8 Positive and negative linear relationships between x and y. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

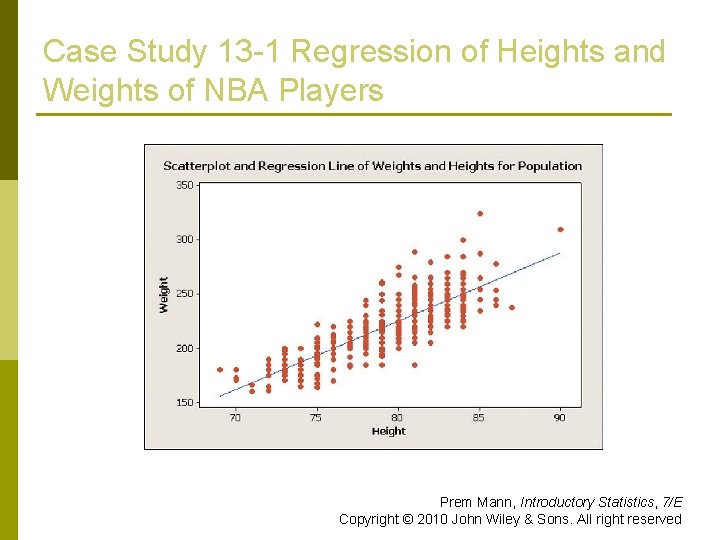
Case Study 13 -1 Regression of Heights and Weights of NBA Players Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

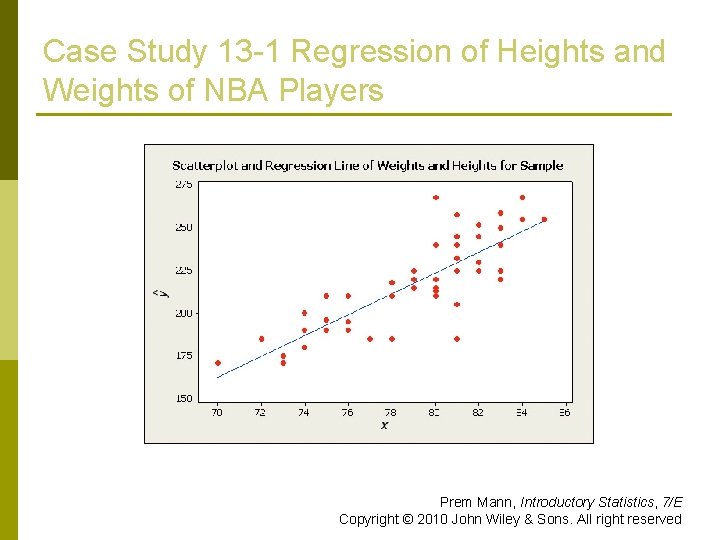
Case Study 13 -1 Regression of Heights and Weights of NBA Players Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Assumptions of the Regression Model Assumption 1: The random error term Є has a mean equal to zero for each x Assumption 2: The errors associated with different observations are independent Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Assumptions of the Regression Model Assumption 3: For any given x, the distribution of errors is normal Assumption 4: The distribution of population errors for each x has the same (constant) standard deviation, which is denoted σЄ Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Assumptions of the Regression Model Assumption 5: The model must be linear in parameters Assumption 6: All the values of x cannot all be the same. Assumption 7: The values of x must be randomly selected. Assumption 8: The error term cannot be correlated with x.

Figure 13. 11 (a) Errors for households with an income of $4000 per month. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Figure 13. 11 (b) Errors for households with an income of $ 7500 per month. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

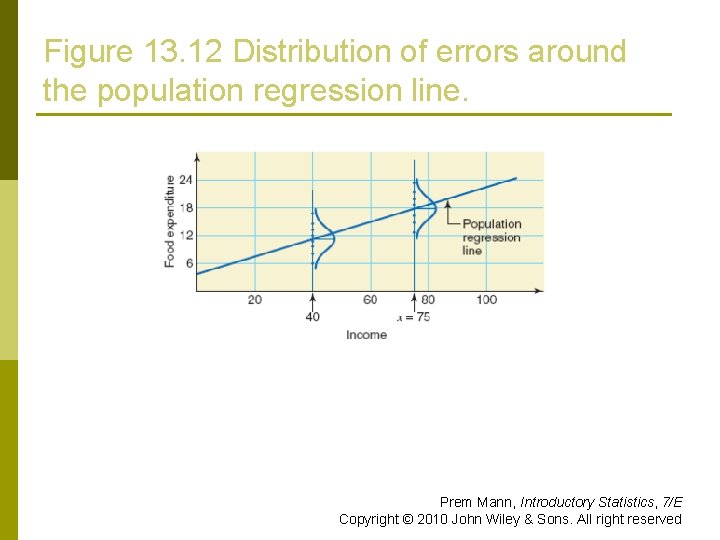
Figure 13. 12 Distribution of errors around the population regression line. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Figure 13. 13 Nonlinear relations between x and y. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

STANDARD DEVIATION OF RANDOM ERRORS Degrees of Freedom for a Simple Linear Regression Model The degrees of freedom for a simple linear regression model are df = n – 2 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

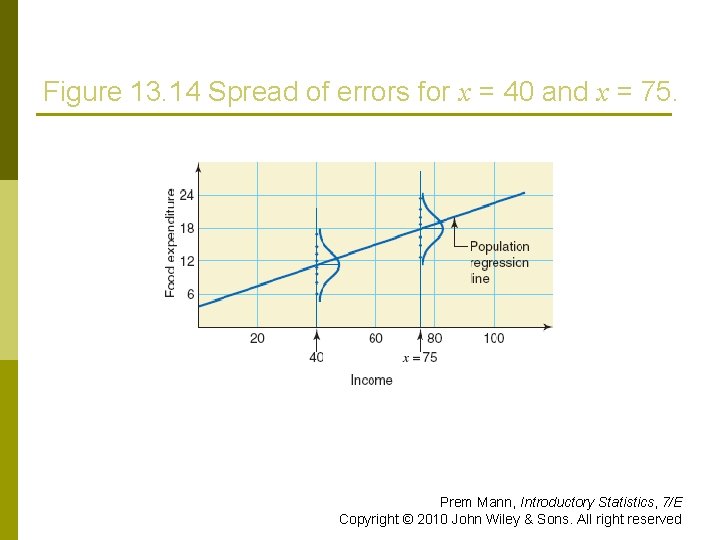
Figure 13. 14 Spread of errors for x = 40 and x = 75. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

STANDARD DEVIATION OF RANDOM ERRORS The standard deviation of errors is calculated as where Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

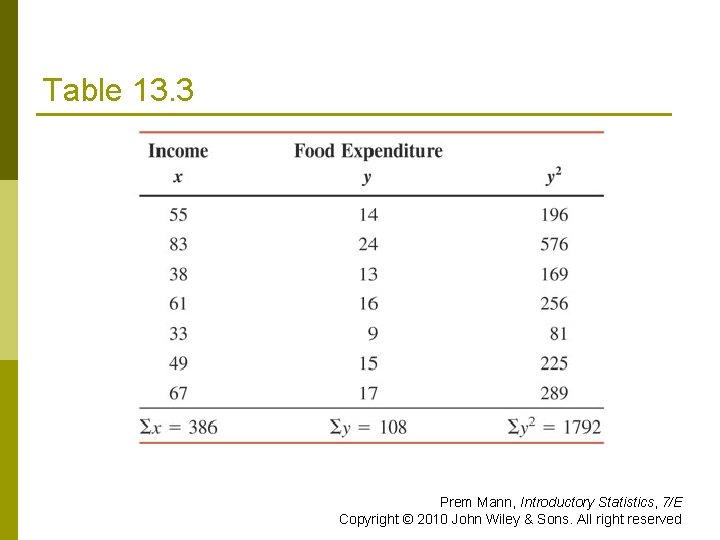
Example 13 -2 Compute the standard deviation of errors se for the data on monthly incomes and food expenditures of the seven households given in Table 13. 1. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Table 13. 3 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -2: Solution Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

COEFFICIENT OF DETERMINATION Total Sum of Squares (SST) The total sum of squares, denoted by SST, is calculated as Note that this is the same formula that we used to calculate SSyy. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

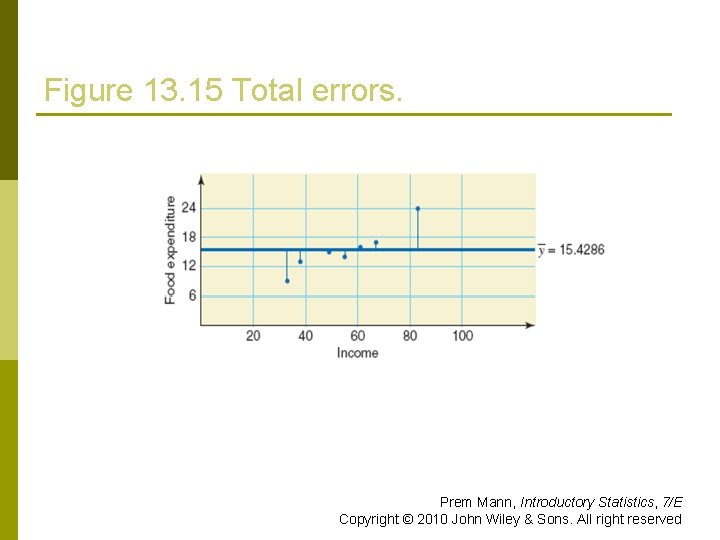
Figure 13. 15 Total errors. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

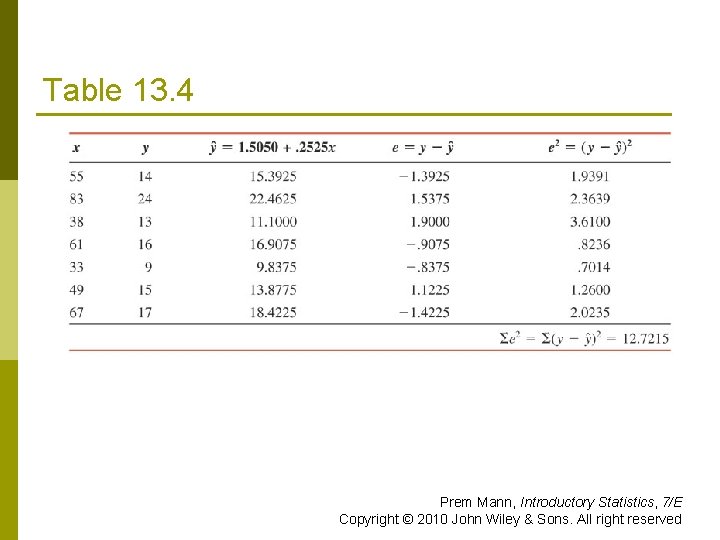
Table 13. 4 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

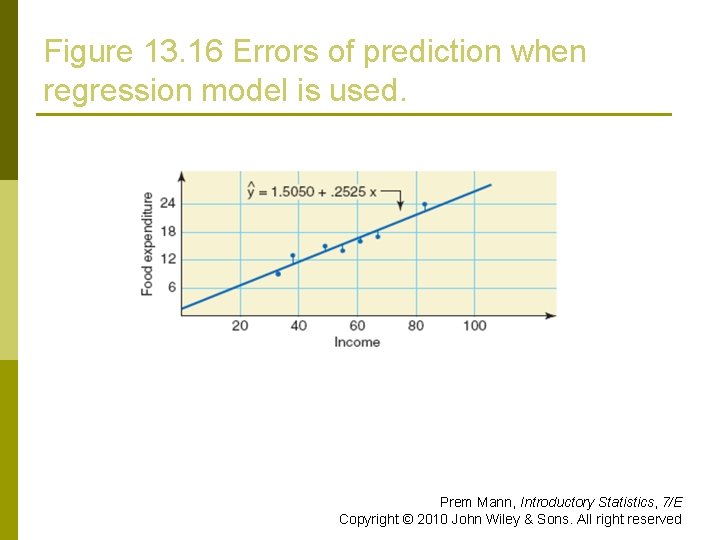
Figure 13. 16 Errors of prediction when regression model is used. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

COEFFICIENT OF DETERMINATION Regression Sum of Squares (SSR) The regression sum of squares , denoted by SSR, is Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

COEFFICIENT OF DETERMINATION Coefficient of Determination The coefficient of determination, denoted by r 2, represents the proportion of SST that is explained by the use of the regression model. The computational formula for r 2 is and 0 ≤ r 2 ≤ 1 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -3 For the data of Table 13. 1 on monthly incomes and food expenditures of seven households, calculate the coefficient of determination. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -3: Solution p p From earlier calculations made in Examples 13 -1 and 13 -2, b =. 2525, SSxx = 447. 5714, SSyy = 125. 7143 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

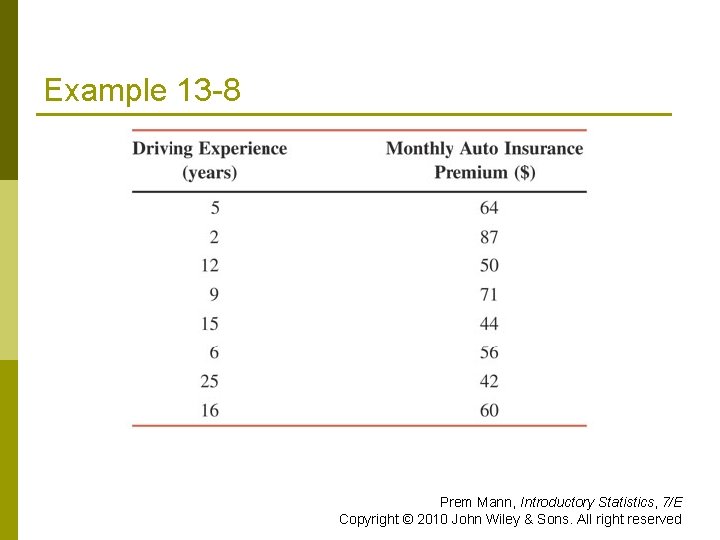
REGRESSION ANALYSIS: A COMPLETE EXAMPLE Example 13 -8 A random sample of eight drivers insured with a company and having similar auto insurance policies was selected. The following table lists their driving experience (in years) and monthly auto insurance premiums. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8 a) Does the insurance premium depend on the driving experience or does the driving experience depend on the insurance premium? Do you expect a positive or a negative relationship between these two variables? b) Compute SSxx, SSyy, and SSxy. c) Find the least squares regression line by choosing appropriate dependent and independent variables based on your answer in part a. d) Interpret the meaning of the values of a and b calculated in part c. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8 e) Plot the scatter diagram and the regression line. f) Calculate r and r 2 and explain what they mean. g) Predict the monthly auto insurance for a driver with 10 years of driving experience. h) Compute the standard deviation of errors. i) Construct a 90% confidence interval for B. j) Test at the 5% significance level whether B is negative. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution a) Based on theory and intuition, we expect the insurance premium to depend on driving experience n n The insurance premium is a dependent variable The driving experience is an independent variable Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

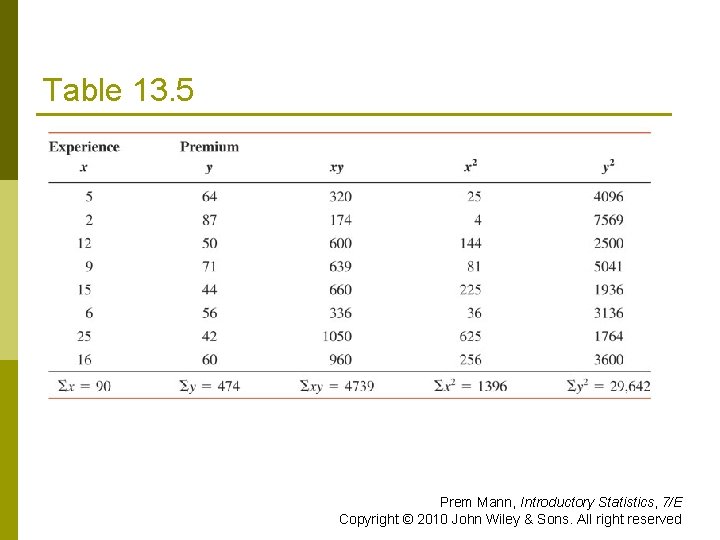
Table 13. 5 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution b) Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution c) Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution d) The value of a = 76. 6605 gives the value of ŷ for x = 0; that is, it gives the monthly auto insurance premium for a driver with no driving experience. The value of b = -1. 5476 indicates that, on average, for every extra year of driving experience, the monthly auto insurance premium decreases by $1. 55. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

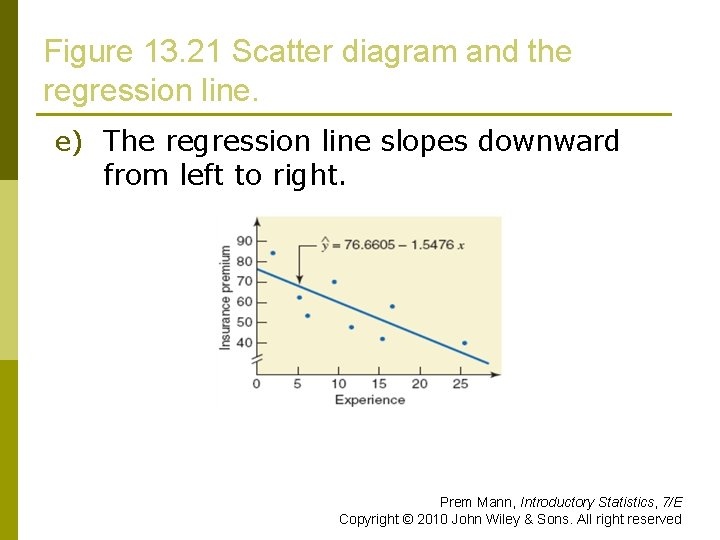
Figure 13. 21 Scatter diagram and the regression line. e) The regression line slopes downward from left to right. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution f) Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution f) The value of r = -0. 77 indicates that the driving experience and the monthly auto insurance premium are negatively related. The (linear) relationship is strong but not very strong. The value of r² = 0. 59 states that 59% of the total variation in insurance premiums is explained by years of driving experience and 41% is not. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution g) Using the estimated regression line, we find the predict value of y for x = 10 is ŷ = 76. 6605 – 1. 5476(10) = $61. 18 Thus, we expect the monthly auto insurance premium of a driver with 10 years of driving experience to be $61. 18. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution h) Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution i) Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution j) § § § Step 1: H 0: B = 0 (B is not negative) H 1: B < 0 (B is negative) Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

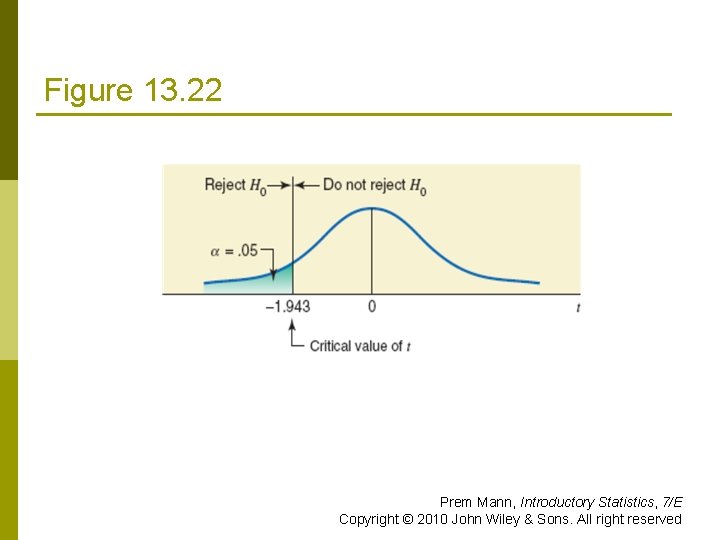
Example 13 -8: Solution p Step 2: Because the standard deviation of the error is not known, we use the t distribution to make the hypothesis test Step 3: p Area in the left tail = α =. 05 p df = n – 2 = 8 – 2 = 6 p The critical value of t is -1. 943 p Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Figure 13. 22 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution Step 4: From H 0 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 13 -8: Solution Step 5: p The value of the test statistic t = -2. 937 p n It falls in the rejection region Hence, we reject the null hypothesis and conclude that B is negative p The monthly auto insurance premium decreases with an increase in years of driving experience. p Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved