Chapter 13 RepeatedMeasures and TwoFactor Analysis of Variance

Chapter 13 Repeated-Measures and Two-Factor Analysis of Variance Power. Point Lecture Slides Essentials of Statistics for the Behavioral Sciences Eighth Edition by Frederick J. Gravetter and Larry B. Wallnau

Chapter 13 Learning Outcomes 1 • Understand logic of repeated-measures ANOVA study 2 • Compute repeated-measures ANOVA to evaluate mean differences for single-factor repeated-measures study 3 • Measure effect size, perform post hoc tests and evaluate assumptions required for single-factor repeated-measures ANOVA

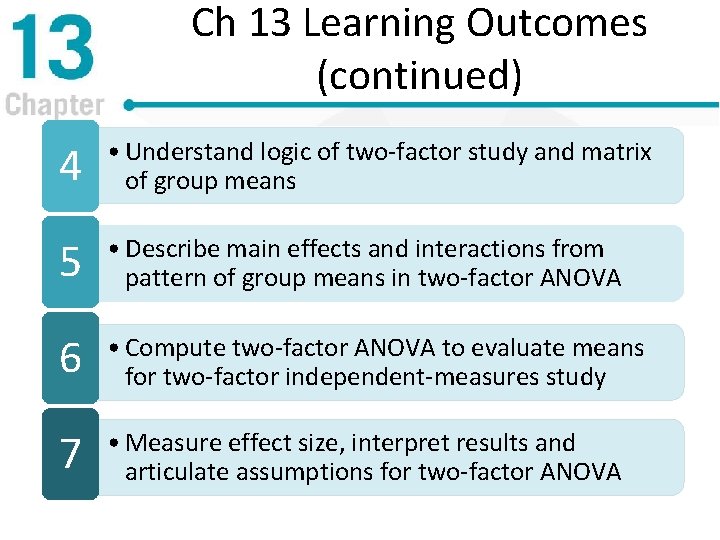
Ch 13 Learning Outcomes (continued) 4 • Understand logic of two-factor study and matrix of group means 5 • Describe main effects and interactions from pattern of group means in two-factor ANOVA 6 • Compute two-factor ANOVA to evaluate means for two-factor independent-measures study 7 • Measure effect size, interpret results and articulate assumptions for two-factor ANOVA

Tools You Will Need • Independent-Measures Analysis of Variance (Chapter 12) • Repeated-Measures Designs (Chapter 11) • Individual Differences

13. 1 Overview • Analysis of Variance – Evaluated mean differences for two or more groups – Limited to one independent variable (IV) • Complex Analysis of Variance – Samples are related; not independent (Repeated-measures ANOVA) – Two independent variables are manipulated (Factorial ANOVA; only Two-Factor in this text)

13. 2 Repeated-Measures ANOVA • Independent-measures ANOVA uses multiple participant samples to test the treatments • Participant samples may not be identical • If groups are different, what was responsible? – Treatment differences? – Participant group differences? • Repeated-measures solves this problem by testing all treatments using one sample of participants

Repeated-Measures ANOVA • Repeated-Measures ANOVA used to evaluate mean differences in two general situations – In an experiment, compare two or more manipulated treatment conditions using the same participants in all conditions – In a nonexperimental study, compare a group of participants at two or more different times • Before therapy; After therapy; 6 -month follow-up • Compare vocabulary at age 3, 4 and 5

Repeated-Measures ANOVA Hypotheses • Null hypothesis: in the population there are no mean differences among the treatment groups • Alternate hypothesis: there is one (or more) mean differences among the treatment groups H 1: At least one treatment mean μ differs from another

General structure of the ANOVA F-Ratio • F ratio based on variances – Numerator measures treatment mean differences – Denominator measures treatment mean differences when there is no treatment effect – Large F-ratio greater treatment differences than would be expected with no treatment effects

Individual differences • Participant characteristics may vary considerably from one person to another • Participant characteristics can influence measurements (Dependent Variable) • Repeated measures design allows control of the effects of participant characteristics – Eliminated from the numerator by the research design – Must be removed from the denominator statistically

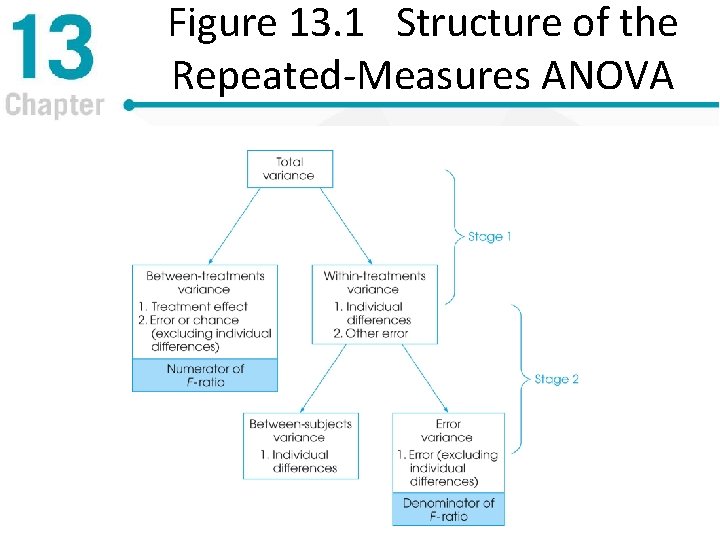
Structure of the F-Ratio for Repeated-Measures ANOVA The biggest change between independentmeasures ANOVA and repeated-measures ANOVA is the addition of a process to mathematically remove the individual differences variance component from the denominator of the F-ratio

Repeated-Measures ANOVA Logic • Numerator of the F ratio includes – Systematic differences caused by treatments – Unsystematic differences caused by random factors are reduced because the same individuals are in all treatments • Denominator estimates variance reasonable to expect from unsystematic factors – Effect of individual differences is removed – Residual (error) variance remains

Figure 13. 1 Structure of the Repeated-Measures ANOVA

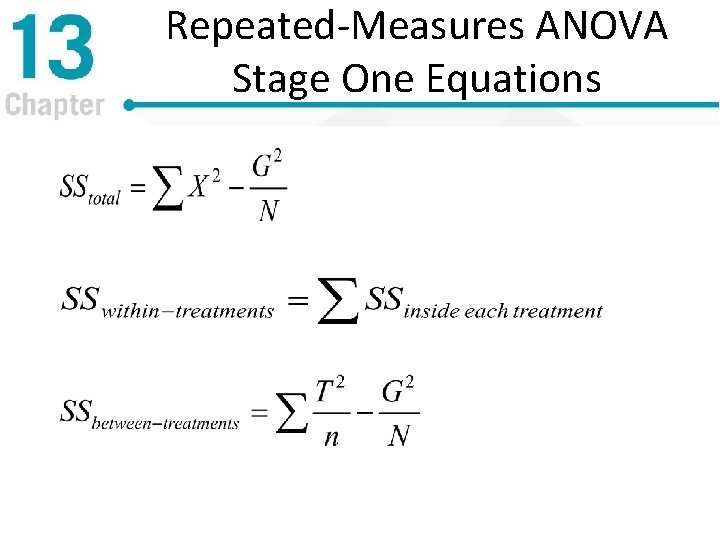
Repeated-Measures ANOVA Stage One Equations

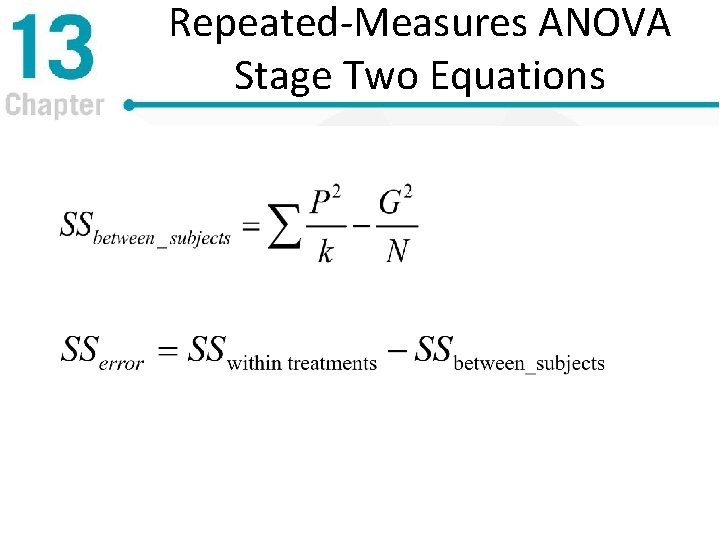
Two Stages of the Repeated. Measures ANOVA • First stage – Identical to independent samples ANOVA – Compute SStotal, SSbetween treatments and SSwithin treatments • Second stage – Done to remove the individual differences from the denominator – Compute SSbetween subjects and subtract it from SSwithin treatments to find SSerror (also called residual)

Repeated-Measures ANOVA Stage Two Equations

Degrees of freedom for Repeated-Measures ANOVA dftotal = N – 1 dfwithin treatments = Σdfinside each treatment dfbetween treatments = k – 1 dfbetween subjects = n – 1 dferror = dfwithin treatments – dfbetween subjects

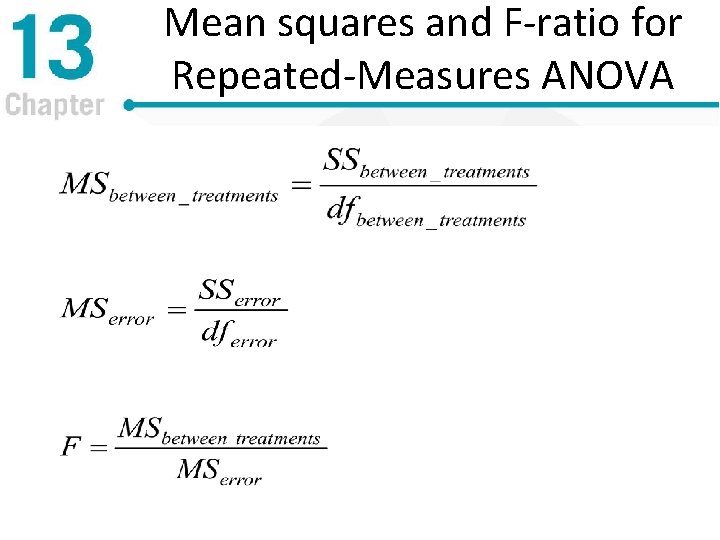
Mean squares and F-ratio for Repeated-Measures ANOVA

F-Ratio General Structure for Repeated-Measures ANOVA

Effect size for the Repeated-Measures ANOVA • Percentage of variance explained by the treatment differences • Partial η 2 is percentage of variability that has not already been explained by other factors or

In the Literature • Report a summary of descriptive statistics (at least means and standard deviations) • Report a concise statement of the ANOVA results – E. g. , F (3, 18) = 16. 72, p<. 01, η 2 =. 859

Repeated Measures ANOVA post hoc tests (posttests) • Significant F indicates that H 0 (“all populations means are equal”) is wrong in some way • Use post hoc test to determine exactly where significant differences exist among more than two treatment means – Tukey’s HSD and Scheffé can be used – Substitute SSerror and dferror in the formulas

Repeated-Measures ANOVA Assumptions • The observations within each treatment condition must be independent • The population distribution within each treatment must be normal • The variances of the population distribution for each treatment should be equivalent

Learning Check • A researcher obtains an F-ratio with df = 2, 12 in a repeated-measures study ANOVA. How many subjects participated in the study? A • 15 B • 14 C • 13 D • 7

Learning Check - Answer • A researcher obtains an F-ratio with df = 2, 12 in a repeated-measures study ANOVA. How many subjects participated in the study? A • 15 B • 14 C • 13 D • 7

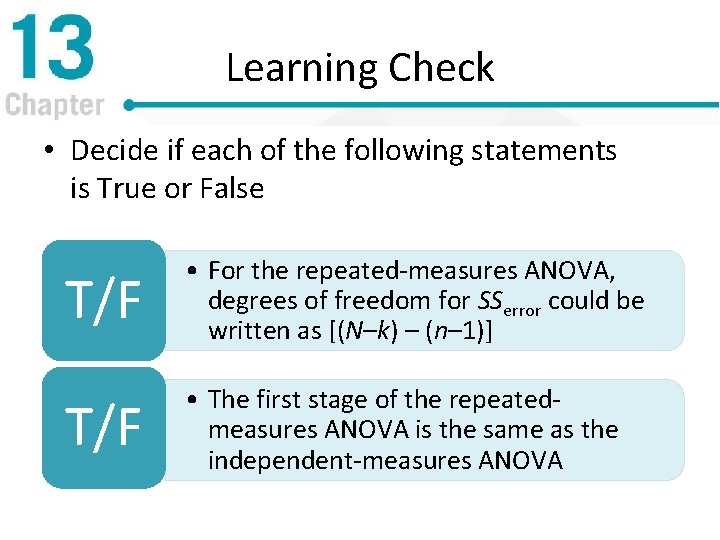
Learning Check • Decide if each of the following statements is True or False T/F • For the repeated-measures ANOVA, degrees of freedom for SSerror could be written as [(N–k) – (n– 1)] T/F • The first stage of the repeatedmeasures ANOVA is the same as the independent-measures ANOVA

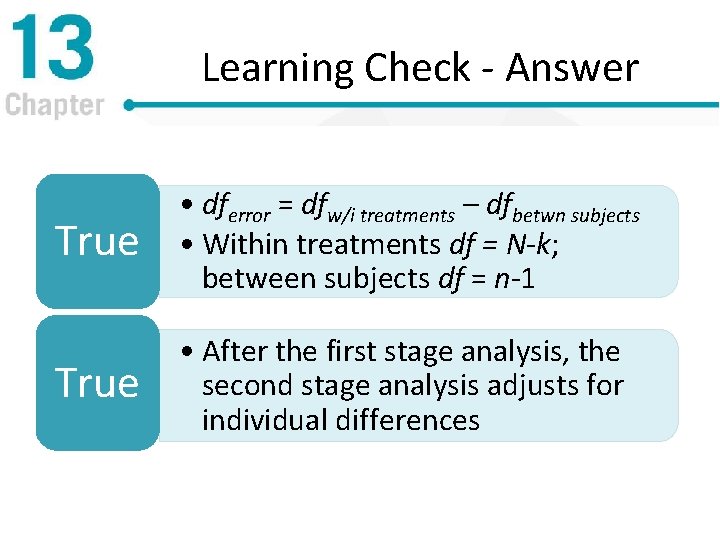
Learning Check - Answer True • dferror = dfw/i treatments – dfbetwn subjects • Within treatments df = N-k; between subjects df = n-1 True • After the first stage analysis, the second stage analysis adjusts for individual differences

Repeated-Measures ANOVA Advantages and Disadvantages • Advantages of repeated-measures designs – Individual differences among participants do not influence outcomes – Smaller number of participants needed to test all the treatments • Disadvantages of repeated-measures designs – Some (unknown) factor other than the treatment may cause participant’s scores to change – Practice or experience may affect scores independently of the actual treatment effect

13. 3 Two-Factor ANOVA • Both independent variables and quasiindependent variables may be employed as factors in Two-Factor ANOVA • An independent variable (factor) is manipulated in an experiment • A quasi-independent variable (factor) is not manipulated but defines the groups of scores in a nonexperimental study

13. 3 Two-Factor ANOVA • Factorial designs – Consider more than one factor • We will study two-factor designs only • Also limited to situations with equal n’s in each group – Joint impact of factors is considered • Three hypotheses tested by three F-ratios – Each tested with same basic F-ratio structure

Main Effects • Mean differences among levels of one factor – Differences are tested for statistical significance – Each factor is evaluated independently of the other factor(s) in the study

Interactions Between Factors • The mean differences between individuals treatment conditions, or cells, are different from what would be predicted from the overall main effects of the factors • H 0: There is no interaction between Factors A and B • H 1: There is an interaction between Factors A and B

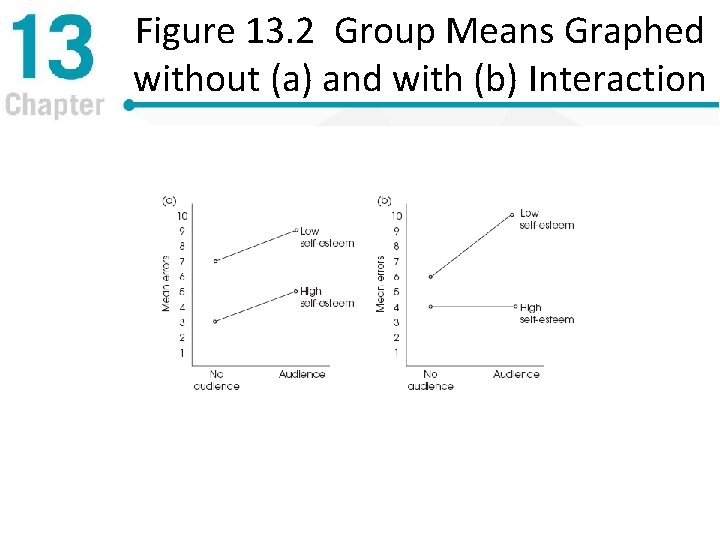
Interpreting Interactions • Dependence of factors – The effect of one factor depends on the level or value of the other – Sometimes called “non-additive” effects because the main effects do not “add” together predictably • Non-parallel lines (cross, converge or diverge) in a graph indicate interaction is occurring • Typically called the A x B interaction

Figure 13. 2 Group Means Graphed without (a) and with (b) Interaction

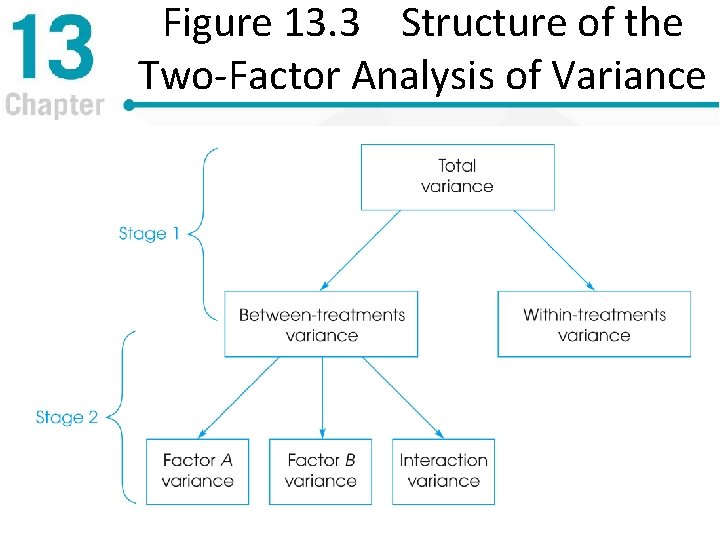
Structure of the Two-Factor Analysis of Variance • Three distinct tests – Main effect of Factor A – Main effect of Factor B – Interaction of A and B • A separate F test is conducted for each • Results of one are independent of the others

Two Stages of the Two-Factor Analysis of Variance • First stage – Identical to independent samples ANOVA – Compute SStotal, SSbetween treatments and SSwithin treatments • Second stage – Partition the SSbetween treatments into three separate components: differences attributable to Factor A; to Factor B; and to the Ax. B interaction

Figure 13. 3 Structure of the Two-Factor Analysis of Variance

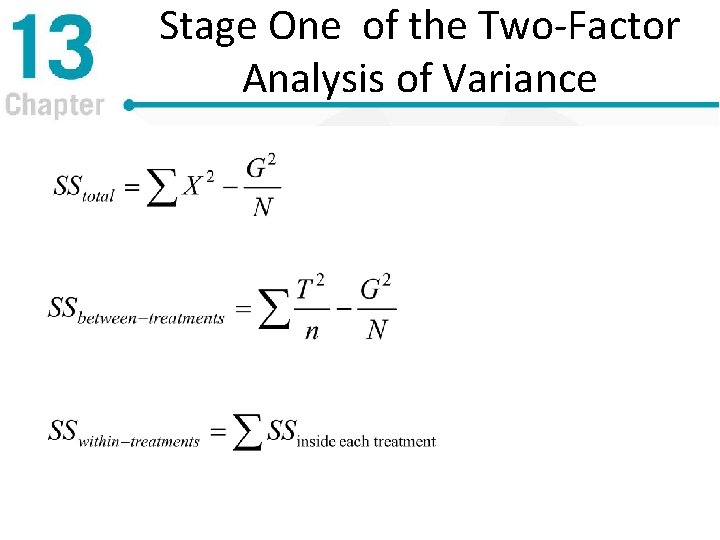
Stage One of the Two-Factor Analysis of Variance

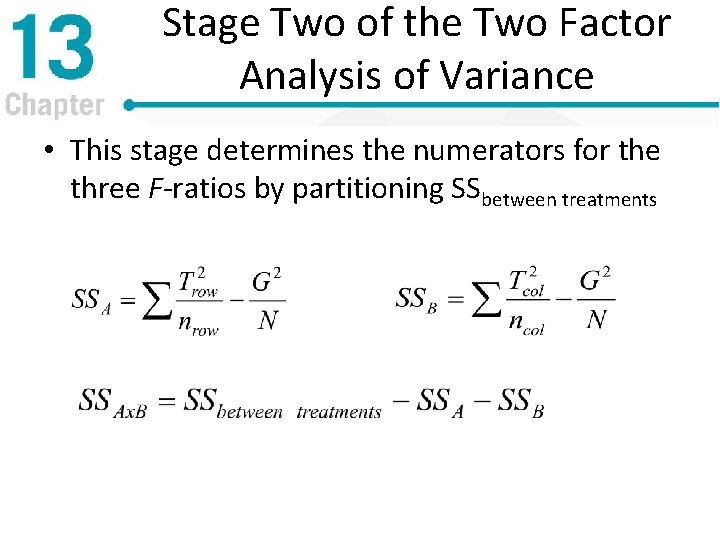
Stage Two of the Two Factor Analysis of Variance • This stage determines the numerators for the three F-ratios by partitioning SSbetween treatments

Degrees of freedom for Two-Factor ANOVA dftotal = N – 1 dfwithin treatments = Σdfinside each treatment dfbetween treatments = k – 1 df. A = (number of rows) – 1 df. B = (number of columns)– 1 dferror = dfwithin treatments – dfbetween subjects

Mean squares and F-ratios for the Two-Factor ANOVA

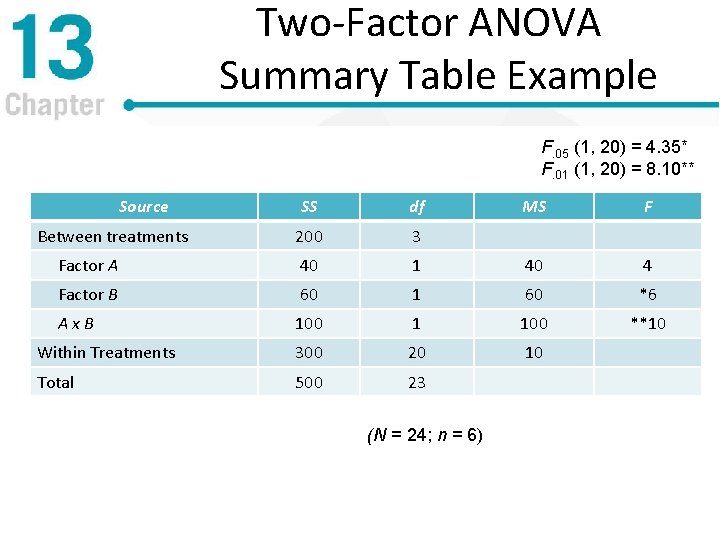
Two-Factor ANOVA Summary Table Example F. 05 (1, 20) = 4. 35* F. 01 (1, 20) = 8. 10** Source SS df MS F 200 3 Factor A 40 1 40 4 Factor B 60 1 60 *6 Ax. B 100 1 100 **10 Within Treatments 300 20 10 Total 500 23 Between treatments (N = 24; n = 6)

Two-Factor ANOVA Effect Size • η 2, is computed to show the percentage of variability not explained by other factors

In the Literature • Report mean and standard deviations (usually in a table or graph due to the complexity of the design) • Report results of hypothesis test for all three terms (A & B main effects; A x B interaction) • For each term include F, df, p-value & η 2 • E. g. , F (1, 20) = 6. 33, p<. 05, η 2 =. 478

Interpreting the Results • Focus on the overall pattern of results • Significant interactions require particular attention because even if you understand the main effects, interactions go beyond what main effects alone can explain. • Extensive practice is typically required to be able to clearly articulate results which include a significant interaction

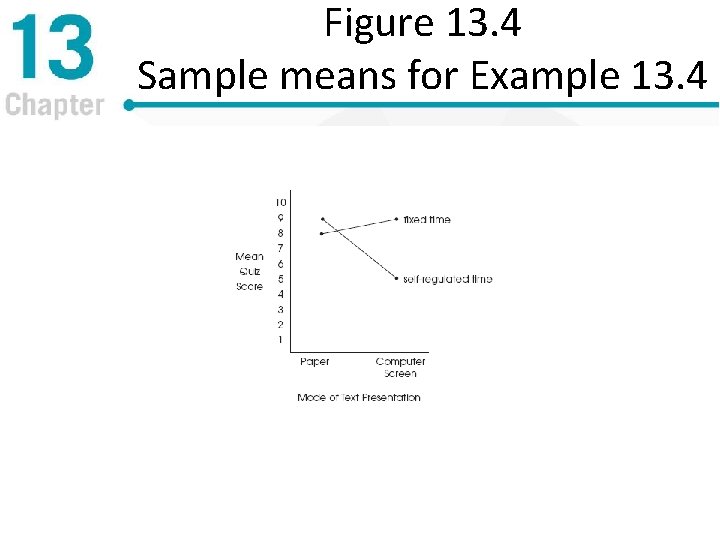
Figure 13. 4 Sample means for Example 13. 4

Two-Factor ANOVA Assumptions • The validity of the ANOVA presented in this chapter depends on three assumptions common to other hypothesis tests – The observations within each sample must be independent of each other – The populations from which the samples are selected must be normally distributed – The populations from which the samples are selected must have equal variances (homogeneity of variance)

Learning Check • If a two-factor analysis of variance produces a statistically significant interaction, then you can conclude that _____ A • either the main effect for factor A or the main effect for factor B is also significant B • neither the main effect for factor A nor the main effect for factor B is significant C • both the man effect for factor A and the main effect for factor B are significant D • the significance of the main effects is not related to the significance of the interaction

Learning Check - Answer • If a two-factor analysis of variance produces a statistically significant interaction, then you can conclude that _____ A • either the main effect for factor A or the main effect for factor B is also significant B • neither the main effect for factor A nor the main effect for factor B is significant C • both the man effect for factor A and the main effect for factor B are significant D • the significance of the main effects is not related to the significance of the interaction

Learning Check • Decide if each of the following statements is True or False T/F • Two separate single-factor ANOVAs provide exactly the same information that is obtained from a two-factor analysis of variance T/F • A disadvantage of combining 2 factors in an experiment is that you cannot determine how either factor would affect participants’ scores if it were examined in an experiment by itself

Learning Check - Answers False • Main effects in Two-Factor ANOVA are identical to results of two One-Way ANOVAs; but Two-Factor ANOVA provides Interaction results too! False • The two-factor ANOVA allows you to determine the effect of one variable controlling for the effect of the other

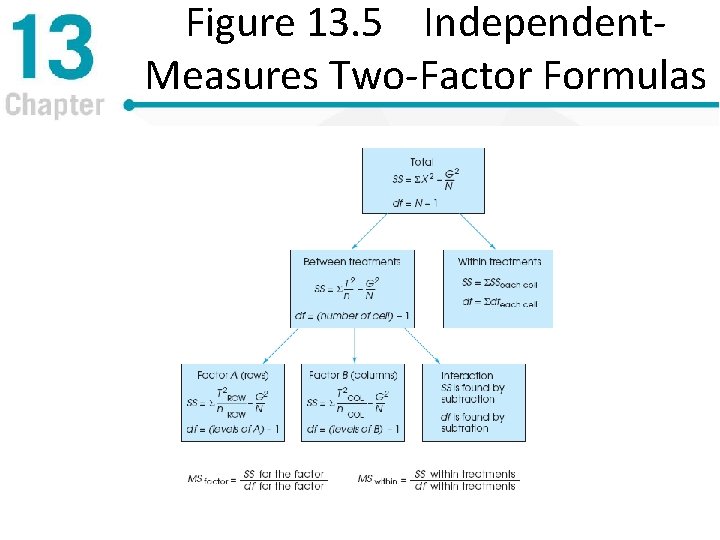
Figure 13. 5 Independent. Measures Two-Factor Formulas

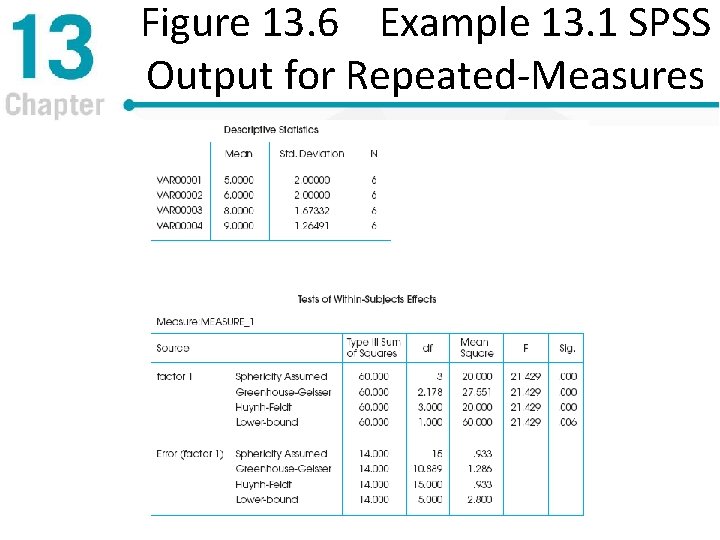
Figure 13. 6 Example 13. 1 SPSS Output for Repeated-Measures

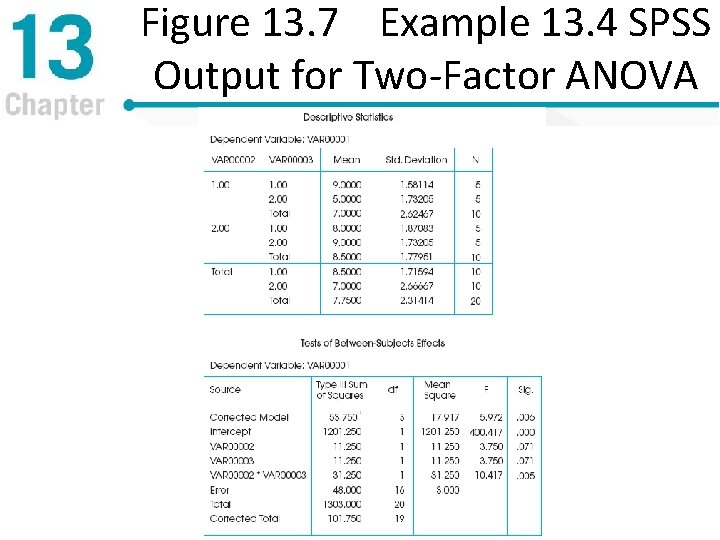
Figure 13. 7 Example 13. 4 SPSS Output for Two-Factor ANOVA

Equations? Concepts? Any Questions ?