Chapter 13 Recursion Starting Out with Programming Logic

Chapter Topics 13. 1 Introduction to Recursion 13. 2 Problem Solving with Recursion 13.

13. 1 Introduction to Recursion A recursive module is a module that calls itself

13. 1 Introduction to Recursion Copyright © 2010 Pearson Education, Inc. Publishing as Pearson

13. 2 Problem Solving with Recursion A problem can be solved with recursion if

13. 2 Problem Solving with Recursion How it works – If the problem can

13. 2 Problem Solving with Recursion Using recursion to calculate the factorial of a

13. 2 Problem Solving with Recursion Continued… Copyright © 2010 Pearson Education, Inc. Publishing

13. 2 Problem Solving with Recursion Copyright © 2010 Pearson Education, Inc. Publishing as

13. 2 Problem Solving with Recursion Inside Program 13 -3 – Inside the function,

13. 2 Problem Solving with Recursion Figure 13 -4 The value of n and

13. 3 Examples of Recursive Algorithms Summing a Range of Array Elements with Recursion

13. 3 Examples of Recursive Algorithms Inside Program 13 -4 – – start and

13. 3 Examples of Recursive Algorithms The Fibonacci Series Continued… Copyright © 2010 Pearson

13. 3 Examples of Recursive Algorithms The Fibonacci Series Copyright © 2010 Pearson Education,

13. 3 Examples of Recursive Algorithms Inside Program 13 -5 – The Fibonacci numbers

13. 3 Examples of Recursive Algorithms Additional examples that can be solved with recursion

13. 3 Examples of Recursive Algorithms Recursion vs. Looping – Reasons not to use

Slides: 19

Download presentation

Chapter Topics 13. 1 Introduction to Recursion 13. 2 Problem Solving with Recursion 13. 3 Examples of Recursive Algorithms Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -2

13. 1 Introduction to Recursion A recursive module is a module that calls itself – When this happens, it becomes like an infinite loop because there may be no way to break out – Depth of Recursion is the number of times that a module calls itself – Recursion should be written so that it can eventually break away – This can be done with an If statement Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -3

13. 2 Problem Solving with Recursion A problem can be solved with recursion if it can be broken down into successive smaller problems that are identical to the overall problems – This process is never required, as a loop can do the same thing – It is generally less efficient to use than loops because it causes more overhead (use of system resources such as memory) Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -5

13. 2 Problem Solving with Recursion How it works – If the problem can be solved now, then the module solves it and ends – If not, then the module reduces it to a smaller but similar problem and calls itself to solve the smaller problem – A Base Case is where a problem can be solved without recursion – A Recursive Case is where recursion is used to solve the problem Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -6

13. 2 Problem Solving with Recursion Using recursion to calculate the factorial of a number – A factorial is defined as n! whereas n is the number you want to solve – 4! or “four factorial” mean 1*2*3*4 = 24 – 5! or “five factorial” means 1*2*3*4*5 = 120 – 0! is always 1 • Factorials are often solved using recursion Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -7

13. 2 Problem Solving with Recursion Inside Program 13 -3 – Inside the function, if n is 0, then the function returns a 1, as the problem is solved – Else, Return n * factorial(n-1) is processed and the function is called again – While the Else does return a value, it does not do that until the value of factorial(n-1) is solved Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -10

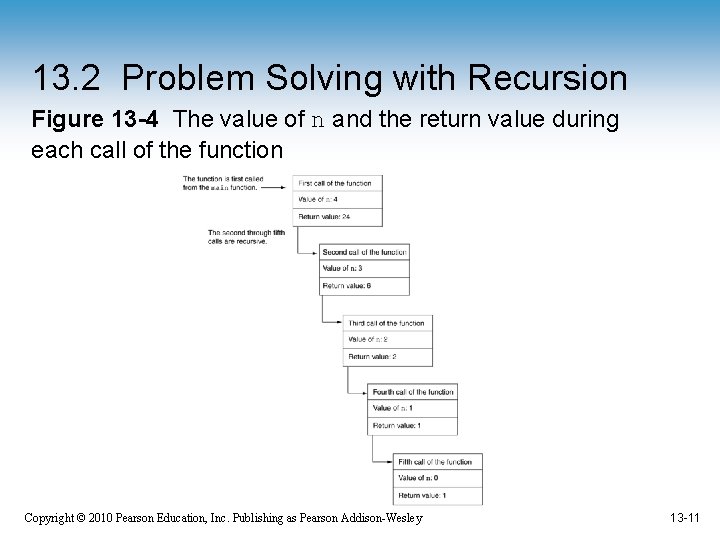
13. 2 Problem Solving with Recursion Figure 13 -4 The value of n and the return value during each call of the function Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -11

13. 3 Examples of Recursive Algorithms Inside Program 13 -4 – – start and end represent the array range Return array[start] + range. Sum(array, start+1), end) • This continuously returns the value of the first element in the range plus the sum of the rest of the elements in the range • It only breaks out when start is greater than end • start must be incremented Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -14

13. 3 Examples of Recursive Algorithms Inside Program 13 -5 – The Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21… – After the second number, each number in the series is the sum of the two previous numbers – The recursive function continuously processes the calculation until the limit is reached as defined in the for loop in the main module Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -17

13. 3 Examples of Recursive Algorithms Additional examples that can be solved with recursion – The Greatest Common Divisor – A Recursive Binary Search – The Towers of Hanoi Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -18

13. 3 Examples of Recursive Algorithms Recursion vs. Looping – Reasons not to use recursion • • They are certainly less efficient than iterative algorithms because of the overhead Harder to discern what is going on with recursion – Why use recursion • The speed and amount of memory available to modern computers diminishes the overhead factor – The decision is primarily a design choice Copyright © 2010 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 13 -19