Chapter 13 Recursion Java Programming From Problem Analysis

Chapter 13: Recursion Java Programming: From Problem Analysis to Program Design, Fourth Edition

Chapter Objectives s Learn about recursive definitions. s Explore the base case and the general case of a recursive definition. s Learn about recursive algorithms. s Learn about recursive methods. s Become aware of direct and indirect recursion. s Explore how to use recursive methods to implement recursive algorithms. Java Programming: From Problem Analysis to Program Design, Second Edition 2

Recursive Definitions s Recursion: s Process of solving a problem by reducing it to smaller versions of itself. s Recursive definition: s Definition in which a problem is expressed in terms of a smaller version of itself. s Has one or more base cases. Java Programming: From Problem Analysis to Program Design, Second Edition 3

Recursive Definitions s Recursive algorithm: s Algorithm that finds the solution to a given problem by reducing the problem to smaller versions of itself. s Has one or more base cases. s Implemented using recursive methods. s Recursive method: s Method that calls itself. s Base case: s Case in recursive definition in which the solution is obtained directly. s Stops the recursion. Java Programming: From Problem Analysis to Program Design, Second Edition 4

Recursive Definitions s General solution: s Breaks problem into smaller versions of itself. s General case: s Case in recursive definition in which a smaller version of itself is called. s Must eventually be reduced to a base case. Java Programming: From Problem Analysis to Program Design, Second Edition 5

Tracing a Recursive Method Recursive method: s Has unlimited copies of itself. s Every recursive call has its own: s Code s Set of parameters s Set of local variables Java Programming: From Problem Analysis to Program Design, Second Edition 6

Tracing a Recursive Method s After completing a recursive call: s Control goes back to the calling environment. s Recursive call must execute completely before control goes back to previous call. s Execution in previous call begins from point immediately following recursive call. Java Programming: From Problem Analysis to Program Design, Second Edition 7

Recursive Definitions s Directly recursive: A method that calls itself. s Indirectly recursive: A method that calls another method and eventually results in the original method call. s Tail recursive method: Recursive method in which the last statement executed is the recursive call. s Infinite recursion: The case where every recursive call results in another recursive call. Java Programming: From Problem Analysis to Program Design, Second Edition 8

Designing Recursive Methods s Understand problem requirements. s Determine limiting conditions. s Identify base cases. Java Programming: From Problem Analysis to Program Design, Second Edition 9

Designing Recursive Methods s Provide direct solution to each base case. s Identify general cases. s Provide solutions to general cases in terms of smaller versions of general cases. Java Programming: From Problem Analysis to Program Design, Second Edition 10

Recursive Factorial Method public static int fact(int num) { if (num = = 0) return 1; else return num * fact(num – 1); } Java Programming: From Problem Analysis to Program Design, Second Edition 11

Recursive Factorial Method Java Programming: From Problem Analysis to Program Design, Second Edition 12

Largest Value in Array public static int largest(int[] list, int lower. Index, int upper. Index) { int max; if (lower. Index == upper. Index) return list[lower. Index]; else { max = largest(list, lower. Index + 1, upper. Index); if (list[lower. Index] >= max) return list[lower. Index]; else return max; } } Java Programming: From Problem Analysis to Program Design, Second Edition 13

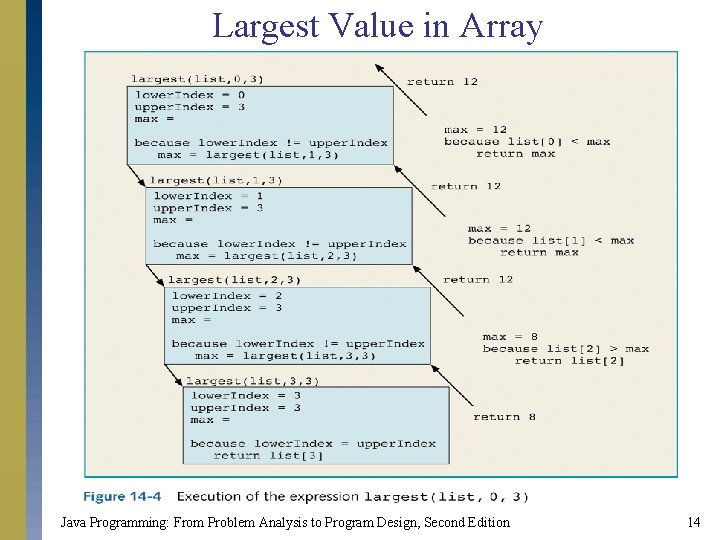
Largest Value in Array Java Programming: From Problem Analysis to Program Design, Second Edition 14

Recursive Fibonacci Java Programming: From Problem Analysis to Program Design, Second Edition 15

Recursive Fibonacci public static int r. Fib. Num(int a, int b, int n) { if(n = = 1) return a; else if (n = = 2) return b; else return r. Fib. Num(a, b, n -1) + r. Fib. Num(a, b, n - 2); } Java Programming: From Problem Analysis to Program Design, Second Edition 16

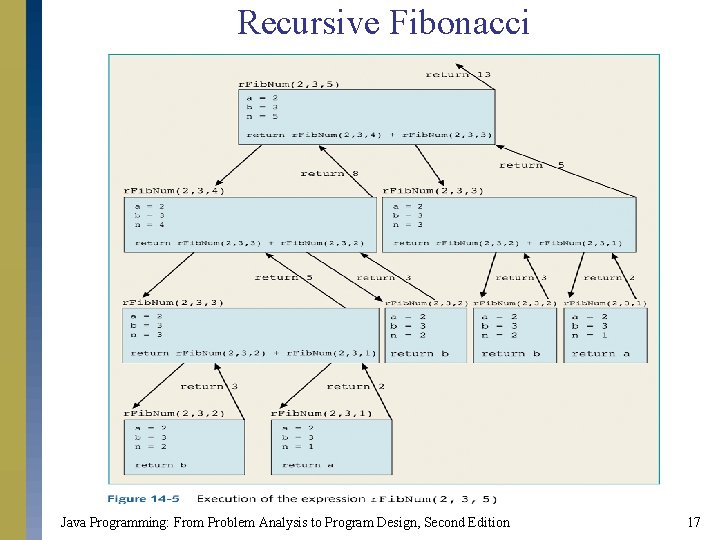
Recursive Fibonacci Java Programming: From Problem Analysis to Program Design, Second Edition 17

Towers of Hanoi: Three Disk Problem Java Programming: From Problem Analysis to Program Design, Second Edition 18

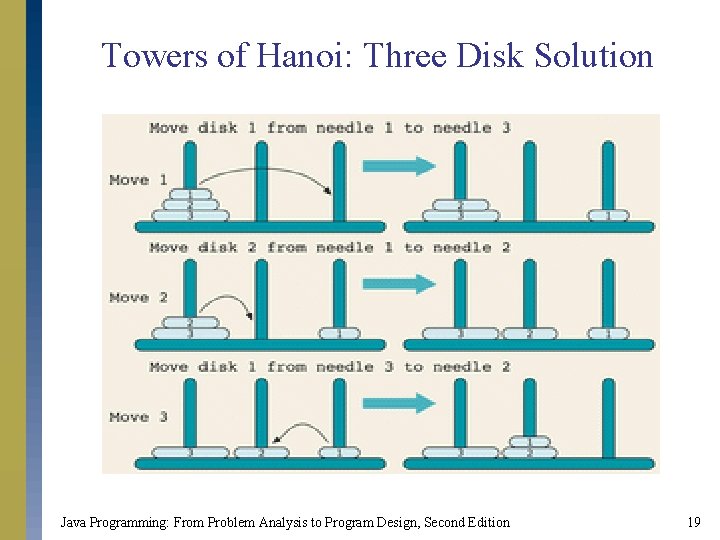
Towers of Hanoi: Three Disk Solution Java Programming: From Problem Analysis to Program Design, Second Edition 19

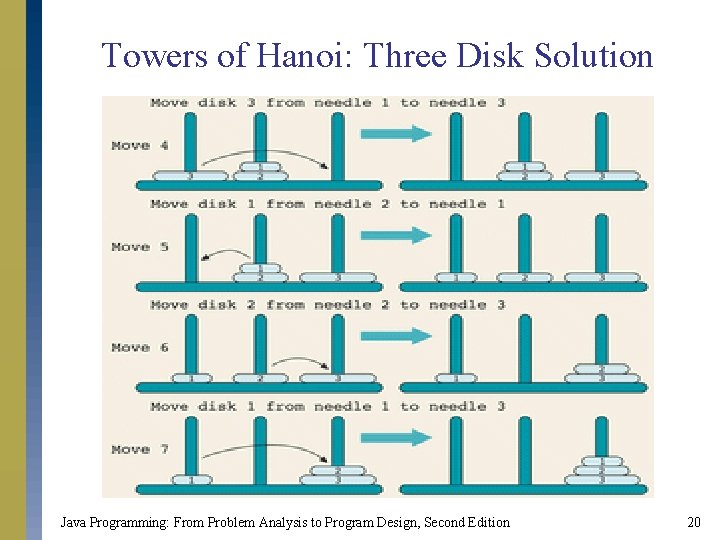
Towers of Hanoi: Three Disk Solution Java Programming: From Problem Analysis to Program Design, Second Edition 20

Towers of Hanoi: Recursive Algorithm public static void move. Disks(int count, int needle 1, int needle 3, int needle 2) { if (count > 0) { move. Disks(count - 1, needle 2, needle 3); System. out. println("Move disk " + count + " from needle " + needle 1 + " to needle " + needle 3 + ". "); move. Disks(count - 1, needle 2, needle 3, needle 1); } } Java Programming: From Problem Analysis to Program Design, Second Edition 21

Recursion or Iteration? s Two ways to solve particular problem: s Iteration s Recursion s Iterative control structures use looping to repeat a set of statements. s Tradeoffs between two options: s Sometimes recursive solution is easier. s Recursive solution is often slower. Java Programming: From Problem Analysis to Program Design, Second Edition 22

Programming Example: Decimal to Binary public static void dec. To. Bin(int num, int base) { if (num > 0) { dec. To. Bin(num / base, base); System. out. print(num % base); } } Java Programming: From Problem Analysis to Program Design, Second Edition 23

Programming Example: Decimal to Binary Java Programming: From Problem Analysis to Program Design, Second Edition 24

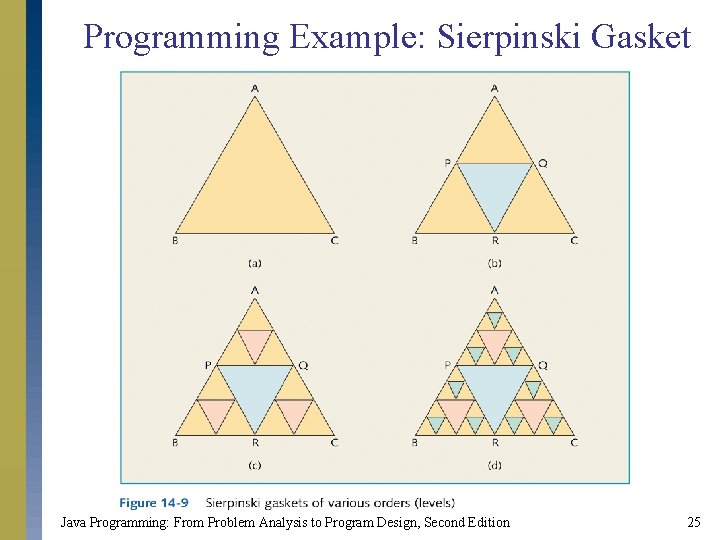
Programming Example: Sierpinski Gasket Java Programming: From Problem Analysis to Program Design, Second Edition 25

Programming Example: Sierpinski Gasket s Input: Non-negative integer that indicates level of Sierpinski gasket. s Output: Triangle shape that displays a Sierpinski gasket of the given order. s Solution includes: s Recursive method draw. Sierpinski. s Method to find midpoint of two points. Java Programming: From Problem Analysis to Program Design, Second Edition 26

Programming Example: Sierpinski Gasket private void draw. Sierpinski(Graphics g, int lev, Point p 1, Point p 2, Point p 3) { Point mid. P 1 P 2; Point mid. P 2 P 3; Point mid. P 3 P 1; if (lev > 0) { g. draw. Line(p 1. x, p 1. y, p 2. x, p 2. y); g. draw. Line(p 2. x, p 2. y, p 3. x, p 3. y); g. draw. Line(p 3. x, p 3. y, p 1. x, p 1. y); mid. P 1 P 2 = mid. Point(p 1, p 2); mid. P 2 P 3 = mid. Point(p 2, p 3); mid. P 3 P 1 = mid. Point(p 3, p 1); draw. Sierpinski(g, lev - 1, p 1, mid. P 1 P 2, mid. P 3 P 1); draw. Sierpinski(g, lev - 1, p 2, mid. P 2 P 3, mid. P 1 P 2); draw. Sierpinski(g, lev - 1, p 3, mid. P 3 P 1, mid. P 2 P 3); } } Java Programming: From Problem Analysis to Program Design, Second Edition 27

Programming Example: Sierpinski Gasket Java Programming: From Problem Analysis to Program Design, Second Edition 28

Chapter Summary s Recursive definitions s Recursive algorithms s Recursive methods s Base cases s General cases Java Programming: From Problem Analysis to Program Design, Second Edition 29

Chapter Summary s Tracing recursive methods s Designing recursive methods s Varieties of recursive methods s Recursion vs. iteration s Various recursive functions Java Programming: From Problem Analysis to Program Design, Second Edition 30