Chapter 13 Introduction to Analysis of Variance Statistics

Chapter 13 Introduction to Analysis of Variance Statistics for the Behavioral Sciences Eighth Edition by Frederick J. Gravetter and Larry B. Wallnau

Chapter 13 Learning Outcomes 1 • Explain purpose and logic of Analysis of Variance 2 • Perform Analysis of Variance on data from single-factor study 3 • Know why and when to use post-hoc tests 4 • Compute Tukey’s HSD and Scheffé test 5 • Compute η 2 to measure effect size

Concepts to review • Variability (Chapter 4) – Sum of squares – Sample variance – Degrees of freedom • Introduction to hypothesis testing (Chapter 8) – The logic of hypothesis testing • Independent measures t statistic (Chapter 10)

13. 1 Introduction to Analysis of Variance • Analysis of variance – Used to evaluate mean differences between two or more treatments – Uses sample data as basis for drawing general conclusions about populations • Advantage of t test: it can be used to compare more than two treatments at a time

Figure 13. 2 Typical situation in which ANOVA would be used

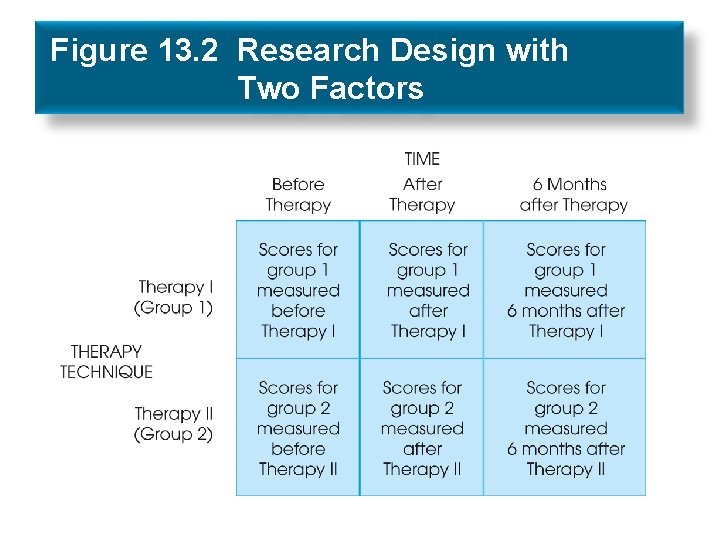
Terminology • Factor – The independent (or quasi-independent) variable that designates the groups being compared • Levels – Individual conditions or values that make up a factor • Factorial design – A study that combines two or more factors

Figure 13. 2 Research Design with Two Factors

Statistical hypotheses for ANOVA • Null hypothesis: the level or value on the factor does not affect the dependent variable. – In the population, the means of the groups do not differ from each other. •

Alternate hypothesis for ANOVA • H 1: There is at least one mean difference among the populations • Several equations are possible – All means are different – Some means are not different, but others are

Test Statistic for ANOVA • F ratio based on variance instead of sample mean differences

Test Statistic for ANOVA • Not possible to compute a sample mean difference between more than two samples • F ratio based on variance instead of sample mean difference – Variance is used to define and measure the size of differences among the sample means (numerator) – Variance in the denominator measures the mean differences that would be expected if there is no treatment effect.

13. 2 Logic of Analysis of Variance • Between-treatments variance – Variability results from general differences between the treatment conditions – Variance between treatments measures differences among sample means • Within-treatments variance – Variability within each sample – Individual scores are not the same within each sample

Sources of Variability Between Treatments • Systematic differences caused by treatments • Random, unsystematic differences – Individual differences – Experimental (measurement) error

Sources of variability within-treatments • No systematic differences related to treatment groups occur within each group • Random, unsystematic differences – Individual differences – Experimental (measurement) error

Figure 13. 4 Partition of total variability into two components

F-ratio • If H 0 is true: – Size of treatment effect is near zero – F is near to 1. 00 • If H 1 is true: – Size of treatment effect is more than 0. – F is noticeably larger than 1. 00 • Denominator of the F-ratio is called the error term

Learning Check • Decide if each of the following statements is True or False. T/F • ANOVA allows researchers to compare several treatment conditions without conducting several hypothesis tests. T/F • If the null hypothesis is true, the F-ratio for ANOVA is expected (on average) to have a value of 0.

Answer True • Several conditions can be compared in one test. False • If the null hypothesis is true, the F -ratio will have a value near 1. 00.

13. 3 ANOVA Notation and Formulas • Number of treatment conditions: k • Number of scores in each treatment: n 1, n 2 etc • Total number of scores: N – When all samples are same size, N = kn • Sum of scores (ΣX) for each treatment: T • Grand total of all scores in study: G = ΣT • There is no universally accepted notation for ANOVA. Other sources may use other symbols.

Figure 13. 5 Structure and sequence of calculations for ANOVA

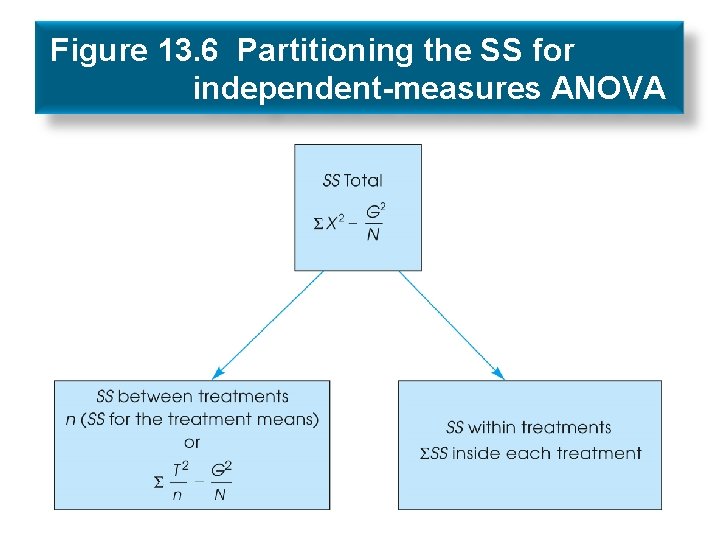
Figure 13. 6 Partitioning the SS for independent-measures ANOVA

ANOVA equations

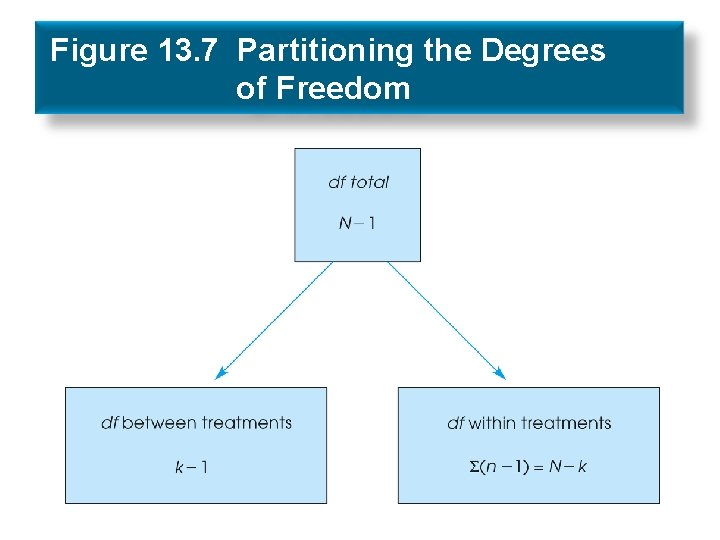
Analysis of degrees of freedom • Total degrees of freedom dftotal= N – 1 • Within-treatments degrees of freedom dfwithin= N – k • Between-treatments degrees of freedom dfbetween= k – 1

Figure 13. 7 Partitioning the Degrees of Freedom

Mean squares and F-ratio

Learning Check • An analysis of variance produces SStotal = 80 and SSwithin = 30. For this analysis, what is SSbetween? A • 50 B • 110 C • 2400 D • More information is needed

Learning Check - Answer • An analysis of variance produces SStotal = 80 and SSwithin = 30. For this analysis, what is SSbetween? A • 50 B • 110 C • 2400 D • More information is needed

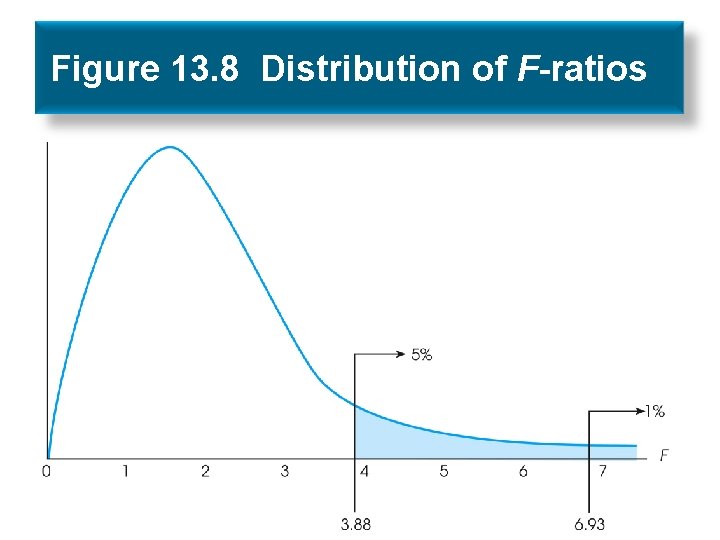
13. 4 Distribution of F-Ratios • If the null hypothesis is true, the value of F will be around 1. 00 • Because F-ratios are computed from two variances, they are always positive numbers. • Table of F values is organized by two df – df numerator (between) – df denominator (within)

Figure 13. 8 Distribution of F-ratios

13. 5 Examples of Hypothesis Testing and Effect Size • Hypothesis tests use the same five steps that have been used in earlier hypothesis tests. • Computation of the test statistic F is done in stages – Compute SStotal, SSbetween, SSwithin – Compute MStotal, MSbetween, MSwithin – Compute F

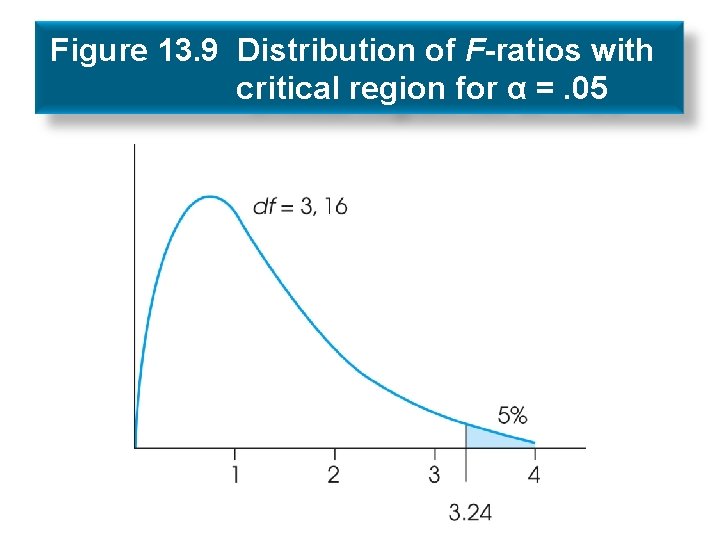
Figure 13. 9 Distribution of F-ratios with critical region for α =. 05

Effect size for ANOVA • Compute percentage of variance accounted for by the treatment conditions • In published reports of ANOVA, usually called η 2 – Same concept as r 2

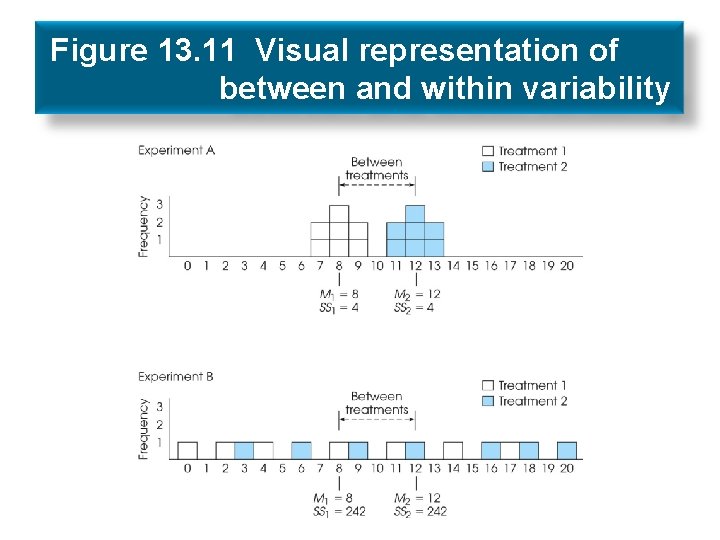
Figure 13. 11 Visual representation of between and within variability

MSwithin and pooled variance • In the t-statistic and in the F-ratio, the variances from the separate samples are pooled together to create one average value for the sample variance • Numerator of F-ratio measures how much difference exists between treatment means. • Denominator measures the variance of the scores inside each treatment

13. 6 Post Hoc Tests • ANOVA compares all individual mean differences simultaneously, in one test • A significant F-ratio (omnibus test) indicates that at least one among the mean differences is statistically significant. – Does not indicate which means differ significantly from each other • Post hoc tests are additional tests done to determine exactly which mean differences are significant, and which are not.

Experimentwise Alpha • Post hoc tests compare two individual means at a time (pairwise comparison) – Each comparison includes risk of a Type I error – Risk of Type I error accumulates and is called the experimentwise alpha level. • Increasing the number of hypothesis tests increases the total probability of a Type I error • Post hoc posttests use special methods to try to control Type I errors

Tukey’s Honestly Significant Difference • A single value that determines the minimum difference between treatment means that is necessary for significance – Honestly Significant Difference (HSD)

The Scheffé Test • The Scheffé test is one of the safest of all possible post hoc tests – Uses an F-ratio to evaluate significance of the difference between two treatment conditions

Learning Check • Which combination of factors is most likely to produce a large value for the F-ratio? A • large mean differences and large sample variances B C • large mean differences and small sample variances • small mean differences and large sample variances D • small mean differences and small sample variances

Learning Check - Answer • Which combination of factors is most likely to produce a large value for the F-ratio? A • large mean differences and large sample variances B C • large mean differences and small sample variances • small mean differences and large sample variances D • small mean differences and small sample variances

Learning Check • Decide if each of the following statements is True or False. T/F • Post hoc tests are needed if the decision from an analysis of variance is to fail to reject the null hypothesis. T/F • A report shows ANOVA results: F(2, 27) = 5. 36, p <. 05. You can conclude that the study used a total of 30 participants.

Answer False • Post hoc tests are only needed when at least one mean difference is significant True • Because dftotal = N-1

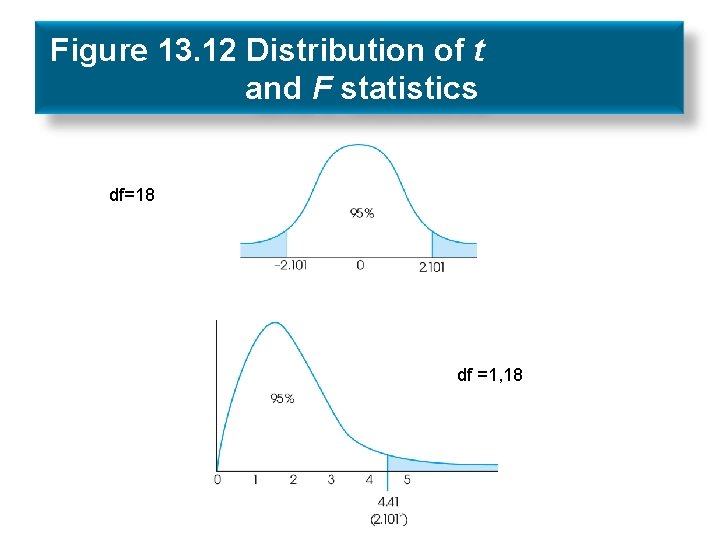
13. 7 Relationship Between ANOVA and t Tests • For two independent samples, either t or F may be used – Always result in same decision – F = t 2 • Usually ANOVA is chosen to examine data where more than two groups are involved for a single factor

Figure 13. 12 Distribution of t and F statistics df=18 df =1, 18

Assumptions for the Independent Measures ANOVA 1. The observations within each sample must be independent 2. The population from which the samples are selected must be normal 3. The populations from which the samples are selected must have equal variances (homogeneity of variance) The assumption of homogeneity of variance is an important one.